2. 福建工程学院信息科学与工程学院, 福建 福州 350118
2. College of Information Science and Engineering, Fujian University of Technology, Fuzhou 350118, China
1 引言
近年来,由于本体的规模日渐庞大,使得本体匹配问题成为一个复杂的(有许多局部最优解的非线性问题)和耗时的问题,针对确定性本体匹配技术[1, 2, 3, 4, 5, 6, 7]难以有效地获取最优的本体匹配结果的问题,基于进化算法的非确定性本体匹配技术受到越来越广泛的关注并被应用在计算次优的本体匹配结果的过程中[8]. 从这一角度不难看出,进化算法[9, 10]可以作为一种有效的确定本体中语义匹配的方法. 已有的基于进化算法的本体匹配技术都要求事先提供标准匹配结果,然而在实际的应用中由于可能的匹配元素的数量随着本体中实体数量的增加而呈现指数级的增长,使得人为无法提供完整的标准匹配结果. 因此,为了解决该问题,部分专家提出设计一种基于局部标准匹配结果的方法,即利用领域专家在合理的时间内提供的一部分标准匹配结果的半自动化本体匹配系统来获取本体匹配结果. 然而,目前尚没有一个基于进化算法的本体匹配系统使用局部标准匹配结果. 此外,最常见的构建局部标准匹配结果的方法是从参考匹配结果中随机选择一个子集以模拟由专家提供匹配元素的过程. 由于这种方法获取的局部标准匹配结果中的匹配元素无法作为完整的参考匹配结果的代表性样本,从而影响所获取的本体匹配结果的质量. 近年来,COMA++[11]、 Falcon-AO[12]、 Lily[13]和GOMMA[14]等前沿本体匹配系统都采用了不同的概念聚类算法将本体划分为具备高内聚度和低耦合度特点的概念分块,这些概念分块中的代表性概念所组成的概念子集能够最大程度地从语义层面反映原本体的概念集合. 目前流行的本体概念聚类算法主要基于结构相似度度量,如针对种类属性的聚类算法ROCK[15]和针对网络体系结构的聚类算法AHSCAN[16],而本文采用的是更为有效的基于临近概念相似度度量的本体概念聚类算法[1]. 本文通过本体概念聚类算法获取原本体的代表性概念子集以构建局部标准匹配结果,并在此基础上建立基于局部标准匹配结果的本体匹配多目标优化模型,提出一种基于局部标准匹配结果的MOEA/D算法(multi-objective evolutionary algorithm based on decomposition)[17]以求解本体匹配问题.
2 利用本体概念聚类算法构建局部标准匹配结果为了构建能够在语义上代表完整标准匹配结果的局部标准匹配结果,需要首先确定两个概念集合以分别代表两个待匹配本体中的所有概念. 为此,本文提出采用本体概念聚类算法来获取这两个概念集合.
2.1 本体概念聚类的内聚度和耦合度通常情况下,本体的概念结构拥有以下两个特点:
(1) 可以通过概念的描述信息(如名字、 标签和备注)来计算概念之间的语义相似度;
(2) 概念结构通常可以表示为有向无圈图,并且泛化关系是本体概念结构中重要的内置关系. 因此,可以从本体概念结构中提取出两类聚类特征,即语义相似度和结构相似度.
本文通过SMOA距离[18]计算概念的描述信息来获取概念间的语义相似度,而概念间的结构相似度通过以下公式计算:
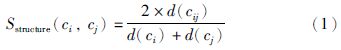
• ci和cj是两个概念,cij是ci和cj的公共父概念;
• d(ci),d(cj)和d(cij)分别是ci,cj和cij在本体概念结构中的深度.
由于在通常情况下,只有邻近概念的结构相似度值才有意义,因此只计算d(ci)-d(cj)<1的两个概念ci和cj的结构相似度.
最后,两个概念间的链接值通过组合语义相似度和概念结构相似度的值来获取:
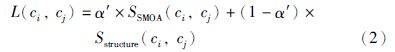
下面进一步阐述概念块中的内聚性和概念块之间的耦合性. 内聚度用于度量同一个概念簇内部概念的链接程度,而耦合度用于度量两个不同概念簇之间的链接程度,这两个度量都可以通过以下公式计算获得:
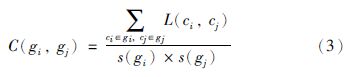
• gi和gj是两个概念簇;
• s(gi)和s(gi)分别是gi和gj的规模.
概念簇gi的内聚度的值为C(gi,gi),概念簇gi和gj的耦合度的值为C(gi,gj).
2.2 本体概念聚类算法在数据挖掘领域中著名的聚类算法Rock[15]的基础上进行改进并提出本体概念聚簇算法. 本体概念聚类算法的目的是将本体中的概念划分为一系列不相交的概念簇g1,g2,…,gn,其中概念簇中内聚度的值越高,概念簇之间耦合度的值就越低. 给定一个本体O,本文的概念聚类算法将O中的每一个概念初始化为一个概念簇,令k为每个概念簇中概念数量的上限. 首先初始化每个概念簇的内聚度和耦合度的值; 然后选择拥有最大内聚度的簇gi以及和gi最大耦合度的概念簇gj,将二者合并后更新O中概念簇集合的耦合度. 该过程不断重复,直到所有概念簇中的概念数量都达到上限或是不存在概念簇的内聚度大于0. 最后,过滤掉那些规模低于阈值的概念簇.
当两个本体中的概念簇集合都获取到以后,根据概念选择比率从所有的簇中随机选择概念以形成两个概念集合,这两个概念集合能够分别在语义上最大程度地表示两个本体中的所有概念. 最后,要求专家确定这两个概念集中的概念匹配关系以构建局部标准匹配结果.
2.3 基于局部标准匹配结果的质量度量局部标准匹配结果是参考匹配结果的子集,给定一个匹配结果A和一个局部标准匹配结果R′,局部匹配结果A′的定义如下:
定义1 局部匹配结果. 局部匹配结果A′是匹配结果A的子集,它包含了所有A中的匹配元素并且至少同R′中的一个匹配元素拥有相同的一个实体: A′={〈e1,e2,n,r〉∈A|∃e′1,n′:〈e′1,e2,n′,r〉∈R′} ∪{〈e1,e2,n,r〉∈A|∃e′2,n′:〈e1,e′2,n′,r〉∈R′}
为了评价通过局部标准匹配结果获取本体匹配结果的质量,以下给出基于局部标准匹配结果的查全率recallp、 查准率precisionp和f度量f-measurep的定义:
定义2 recallp给定一个局部标准匹配结果R′,局部匹配结果A′的查全率由以下公式计算:
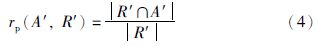
定义3 precisionp. 给定一个局部标准匹配结果R′,局部匹配结果A′的查准率由以下公式计算:
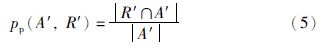
定义4 f-measurep. 给定一个局部标准匹配结果R′,局部匹配结果A′的f度量由以下公式计算:
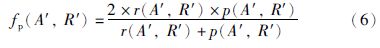
本文希望能够通过确定合适的相似度度量技术的集成
权重来获取最优的本体匹配结果,希望得到本体匹配结果的recallp和precisionp能够同时最大化. 综上,本文提出基于局部标准匹配结果的本体匹配问题的多目标优化模型如下:
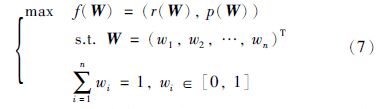
MOEA/D是张青富等[14]提出的一种基于分解的多目标优化算法,该算法将一个多目标优化问题分解为一系列单目标优化子问题,每一个Pareto最优解都是相应的单目标优化子问题的最优解,而MOEA/D正是通过求解不同的单目标优化子问题来获取不同的Pareto最优解. 由于现有的基于单目标进化算法的本体匹配技术无法一次提供多组不同的本体匹配结果以满足决策者不同的要求,为了克服这一缺陷,本文提出采用经典的多目标进化算法MOEA/D来求解本体匹配问题.
4.1 MOEA/D算法代表解的选择本文中选取的代表解是位于Pareto前沿的最优解集中的3个分别拥有最好recallp、 最好precisionp和最好f-measurep的拐点解. 在缺乏准确的决策制定者的偏好的情况下,拐点区域的解可以用于满足拥有不同偏好的决策制定者的要求[19]. 由于在两目标优化问题中,从两个目标矛盾的角度来看,拐点解和偏好的方法之间是有关联的[20]. 具体地说,本文采用如下的选择策略来获取3个具有代表性的拐点解:
(1) 在拥有最好recallp解中选择一个拥有最好precisionp的解;
(2) 在拥有最好precisionp解中选择一个拥有最好recallp的解;
(3) 在拥有最好f-measurep解中,采用max-min方法来选择较好的解: 假设解x1,x2,…,xk都拥有最高的f-measurep,它们的recallp和precisionp的值分别表示为fr(xi)和fp(xi)(i=1,2,…,k),然后通过以下公式来选择较优的解:
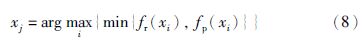
以下举例说明max-min方法的过程. 假设有两个解x1和x2的f-measure值都为0.97,x1的recallp值和precisionp值分别为0.95和1.00,x2的recallp值和precisionp值分别为0.98和0.97. 首先从x1的recallp值和precisionp值中选出较小的值0.95,再从x2的recallp值和precisionp值中选出较小的值0.97. 由于0.97大于0.95,根据max-min方法可以得出x2优于x1. 这个结论意味着相比x1而言,x2对于recallp值和precisionp值的权衡更好.
4.2 针对本体元匹配问题的优化目标的分解本文的两个优化目标是同时最大化recallp和precisionp,在此基础上定义分解的第i个子问题的优化目标为maxrecallp×precisionpαi×recallp+βi×precisionp,假设N是欲分解的子问题数量,(α1,β1)=(0,1),(αi,βi)=i-1N-1,N-iN-1,i=2,3,…,N-1,(αN,βN)=(1,0). 如果权重向量λi=(αi,βi)和λj=(αj,βj)彼此接近(在本文的工作中,根据两个权重向量的欧氏距离来判断两个权重向量是否接近),那么λi和λj对应的第i和第j个子问题是邻居问题,第j个单目标子问题中的信息可用于帮助第i个单目标子问题的寻优过程.
4.3 初始化种群进化算法是一种基于种群的启发式算法,因此初始种群的好坏对种群的搜索性能及最终解的质量具有非常重要的影响. 在标准的进化算法中,初始种群通过随机方式产生,初始种群可能分布不均匀,这就不利于搜索到全局最优解. 本节使用均匀设计[21, 22]方法构造初始种群. 均匀设计方法产生的初始种群能更加均匀地分布在整个可行解空间,也更能从统计意义上反映出所涉及问题的目标函数的特性. 通过均匀设计方法构造初始种群的步骤如下: 令X={(x1,x2,…,xk)0≤x1,x2,…,xk≤1},〈η〉是η的整数部分,p1,p2,…,pk是前k个素数,(γ1,γ2,…,γk)=(p1,p2,…,pk),q是X中均匀分布的点的数量,则(〈zγ1〉,〈zγ2〉,…,〈zγk〉z=1,…,q)是q个在X中均匀分布的点.
4.4 遗传算子• 选择算子: 本文采用赌轮盘选择算子,该算子为每一个个体赋予一个正比于它们的适应度值的选择概率,这就使得适应度值最高的个体拥有最高概率产生下一代个体,而适应度值不是那么高的个体也有机会产生下一代个体.
• 交叉算子: 本文采用单点交叉算子. 单点交叉算子首先随机地选择父个体中的一个编码位作为切割点,切割点将父个体分为左右两个部分,然后通过交换父个体中的右边的基因来产生新个体.
• 变异算子: 本文采用位点变异方法,按照以下公式进行变异:
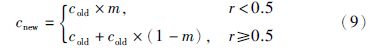
MOEA/D算法流程如图 1所示:
1) 步骤一(初始化)
(1)计算任意两个权重向量间的欧氏距离,以便获取每一个权重向量及其最接近的T个权重向量. 令C(i)={λi1,λi2,…,λiT}(i=1,2,…,N),其中λi1,λi2,…,λiT是向量λi1的T个最接近的权重向量;
(2) 随机生成一个规模为N的初始群体x1,x2,…,
xN,令xi作为第i个子问题的最优解;
(3) 根据4.2小节的选择策略,选出当前初始化群体中的3个代表解.
2) 步骤二(进化)
以下以第i个子问题为例阐述每一个子问题的解的进化过程:
(1) 选择. 根据选择概率,从C(i)中随机选出两个下标为k和l的子问题,k,l∈{1,2,…,T};
(2)交叉. 根据交叉概率执行交叉操作,根据xk和xl生成新的个体y′,交叉算子的执行过程详见3.4小节;
(3) 变异. 根据变异概率执行变异操作,产生新的个体y,变异算子的执行过程详见3.4小节;
(4) 更新邻居子问题的解. 对于C(i)中的第j个元素,如果gws(yλj)≥gws(xjλj),则令xj=y;
(5) 更新群体中的3个代表解. 根据3.1小节的选择策略,尝试使用新个体y更新群体中的3个代表解.
3) 步骤三(终止条件)
如果满足终止条件,则算法输出3个Pareto前沿的代表解; 否则继续执行步骤二.
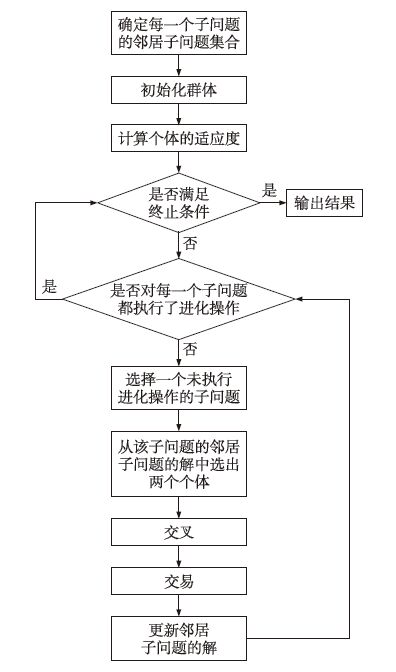
|
| 图 1 MOEA/D算法流程图 Fig. 1 The flow chart of MOEA/D algorithm |
实验中本体概念聚类算法采用以下参数:
• 每个概念簇的最大概念数量为500;
• 概念链接计算中的相似度组合参数α=0.5;
• 过滤概念簇的阈值为1;
• 概念选择比率为0.15. 当概念选择比率为1时,等同于让专家提供完整的参考匹配结果. 通过实验观察到当概念比率值大于0.15时,随着概念比率值的增加,获取的本体匹配结果的质量显著地提升. 然而,目前尚未能解决如何确定合适的概念选择比率来权衡本体匹配结果的质量和专家的工作量.
实验所采用的相似度度量技术为:
• SMOA距离(基于词汇的相似度度量);
• 基于WordNet[23]的相似度度量(基于语言学的相似度度量);
• Similarity Flooding算法[24](基于本体结构的相似度度量).
MOEA/D的参数如下:
• 数值精度为0.01;
• 适应度函数是recallp和precisionp;
• 种群规模是20个个体;
• 交叉概率为0.6;
• 变异概率为0.01;
• 终止条件为达到250次适应度评价或者recallp和precisionp的值都达到1.
5.2 实验结果与分析实验采用本体匹配领域公认的2012年本体匹配评价竞赛(ontology alignment evaluation initiative,OAEI)的测试数据集. 为了同已有的本体匹配系统比较,本文提出的方法所获取的本体匹配结果的质量采用传统的recall、 precision和f-measure重新度量. 表 1和表 2分别给出了由著名的基于遗传算法的本体匹配系统GOAL[25]和MOEA/D在30次独立运行过程后的平均结果. 表 1给出了通过recall和precision来度量本体匹配结果质量的GOAL同MOEA/D的结果,其中第2列和第4列分别是由recall驱动和由precision驱动的GOAL的结果,第3列和第5列分别代表最优recallp和最优precisionp的MOEA/D算法的拐点解. 表 2给出了f-measure驱动的GOAL和MOEA/D代表最优f-measurep的拐点解. 表 3给出了由f-measure驱动的通过随机的方法和通过本体概念聚类的方法构建的局部标准匹配结果的比较. 表 4给出了本文的方法同参与OAEI 2012的前沿本体匹配系统之间的比较. 在表 1~表 4中,符号R和P分别表示recall和precision,表 4中的数值是所有测试案例结果的均值,其中OAEI 2012参与者的数据来自OAEI 2012官方公布的数据.
| 编号 | GOALR(P) | MOEA/DR(P) | GOALP(R) | MOEA/DP(R) |
| 101 | 1.00(0.78) | 1.00(1.00) | 1.00(0.01) | 1.00(1.00) |
| 103 | 1.00(0.68) | 1.00(1.00) | 1.00(0.98) | 1.00(1.00) |
| 104 | 1.00(0.65) | 1.00(1.00) | 1.00(0.99) | 1.00(1.00) |
| 201 | 0.95(0.04) | 1.00(0.01) | 1.00(0.01) | 1.00(0.32) |
| 203 | 1.00(0.41) | 1.00(0.61) | 1.00(0.83) | 1.00(0.98) |
| 204 | 1.00(0.13) | 1.00(0.23) | 1.00(0.74) | 1.00(0.93) |
| 205 | 0.98(0.02) | 0.98(0.02) | 1.00(0.21) | 1.00(0.43) |
| 206 | 0.72(0.03) | 0.73(0.03) | 1.00(0.23) | 1.00(0.23) |
| 221 | 1.00(0.52) | 1.00(1.00) | 1.00(0.99) | 1.00(1.00) |
| 222 | 1.00(0.75) | 1.00(1.00) | 1.00(0.99) | 1.00(1.00) |
| 223 | 1.00(0.27) | 1.00(0.78) | 1.00(0.96) | 1.00(0.98) |
| 224 | 1.00(0.63) | 1.00(1.00) | 1.00(1.00) | 1.00(1.00) |
| 225 | 1.00(0.75) | 1.00(1.00) | 1.00(0.97) | 1.00(1.00) |
| 228 | 1.00(0.68) | 1.00(1.00) | 1.00(1.00) | 1.00(1.00) |
| 230 | 1.00(0.54) | 1.00(1.00) | 1.00(0.97) | 1.00(1.00) |
| 231 | 1.00(0.65) | 1.00(1.00) | 1.00(0.98) | 1.00(1.00) |
| 301 | 0.95(0.03) | 1.00(0.02) | 1.00(0.30) | 1.00(0.36) |
| 302 | 0.91(0.02) | 0.98(0.02) | 1.00(0.25) | 1.00(0.40) |
| 编号 | GOAL f-measure(R,P) | MOEA/D f-measure(R,P) |
| 101 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 103 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 104 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 201 | 0.94(0.90,0.98) | 0.94(0.90,0.98) |
| 203 | 0.99(0.98,1.00) | 0.99(0.98,1.00) |
| 204 | 0.98(0.99,0.98) | 0.98(0.99,0.98) |
| 205 | 0.89(0.90,0.89) | 0.94(0.89,0.99) |
| 206 | 0.70(0.67,0.73) | 0.70(0.67,0.73) |
| 221 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 222 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 223 | 0.99(0.98,1.00) | 0.99(0.98,1.00) |
| 224 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 225 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 228 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 230 | 0.99(1.00,1.00) | 1.00(1.00,1.00) |
| 231 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 301 | 0.75(0.73,0.77) | 0.76(0.78,0.74) |
| 302 | 0.71(0.58,0.90) | 0.71(0.60,0.85) |
| 编号 | 基于随机的方法f-measure(R,P) | 基于聚类的方法f-measure(R,P) |
| 101 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 103 | 0.99(1.00,0.98) | 1.00(1.00,1.00) |
| 104 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 201 | 0.93(0.90,0.97) | 0.94(0.90,0.98) |
| 203 | 0.99(0.98,1.00) | 0.99(0.98,1.00) |
| 204 | 0.96(0.97,0.96) | 0.98(0.99,0.98) |
| 205 | 0.95(0.92,0.89) | 0.94(0.89,0.99) |
| 206 | 0.65(0.51,0.88) | 0.70(0.67,0.73) |
| 221 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 222 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 223 | 0.98(0.98,0.98) | 0.99(0.98,1.00) |
| 224 | 0.99(0.97,1.00) | 1.00(1.00,1.00) |
| 225 | 0.99(1.00,0.98) | 1.00(1.00,1.00) |
| 228 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 230 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 231 | 1.00(1.00,1.00) | 1.00(1.00,1.00) |
| 301 | 0.58(0.90,0.71) | 0.76(0.78,0.74) |
| 302 | 0.66(0.61,0.73) | 0.71(0.60,0.85) |
| 编号 | f-measure | R | P |
| MapSSS | 0.87 | 0.77 | 0.87 |
| YAM++ | 0.83 | 0.72 | 0.83 |
| AROMA | 0.77 | 0.64 | 0.77 |
| AUTOMSv2 | 0.69 | 0.54 | 0.69 |
| WeSeE | 0.69 | 0.53 | 0.69 |
| Hertuda | 0.68 | 0.54 | 0.68 |
| HotMatch | 0.66 | 0.50 | 0.66 |
| Optima | 0.63 | 0.49 | 0.63 |
| MapSSS | 0.54 | 0.54 | 0.87 |
| YAM++ | 0.43 | 0.43 | 0.83 |
| WikiMatch | 0.45 | 0.45 | 0.62 |
| ServOMap | 0.57 | 0.57 | 0.58 |
| LogMap | 0.50 | 0.50 | 0.56 |
| MaasMatch | 0.20 | 0.20 | 0.56 |
| MEDLEY | 0.54 | 0.54 | 0.54 |
| ServOMapLt | 0.54 | 0.82 | 0.33 |
| ASE | 0.43 | 0.54 | 0.51 |
| 本文的方法 | 0.95 | 0.93 | 0.96 |
由表 1可知,除了测试案例205(二者结果一样)以外,MOEA/D获取的代表最优recall的拐点解在剩余的案例中都优于recall驱动的GOAL的解. 例如测试案例201,MOEA/D获取的解的recall高于recall驱动的GOAL的解; 而在测试案例222中,虽然二者的recall是相同的,MOEA/D获取的解的precision高于recall驱动的GOAL的解. 此外,除了测试案例206、 224和228(在这3个案例中,二者的结果相同)以外,MOEA/D获取的代表最优precision的拐点解在剩余的案例中都优于precision驱动的GOAL的解. 由于MOEA/D同时考虑到recall和precision,因此相比仅仅由recall或precision驱动的GOAL而言,更有可能找到更好的解.
由表 2可知,除了测试案例205、 301和302以外,MOEA/D获取的代表最优f-measure的拐点解同f-measure驱动的GOAL的解的质量是相同的. 在测试案例205中,MOEA/D获取代表最优f-measure的拐点解的f-measure高于f-measure驱动的GOAL解. 在测试案例301和302中,根据max-min方法可以得知MOEA/D获取代表最优f-measure的拐点解的f-measure优于f-measure驱动的GOAL解. 由于在进化的过程中,MOEA/D算法可以确保两个目标recallp和precisionp的一致性改进,相比基于传统遗传算法的本体匹配技术而言,基于MOEA/D的本体匹配技术在求解本体匹配问题的过程中具有更高的概率找到更优的解.
由表 3可知,除了测试数据集205,基于本体概念聚类方法的结果都优于基于随机方法的结果. 不仅如此,除了测试数据集301以外,基于本体概念聚类方法的结果的precision都高于基于随机方法的结果,在一些测试数据集中recall的值也较高. 由于基于本体概念聚类方法构建的局部标准匹配结果能更好地从语义上表示参考匹配结果,因此可以获取更高质量本体匹配结果.
由表 4可知,本文方法获取的本体匹配结果的f-measure、 recall和precision值优于所有OAEI 2012的参与者.
综上,本文提出的方法在获取本体匹配结果方面总体上优于基于遗传算法的本体匹配技术、 基于随机方法构建的局部标准匹配结果的本体匹配技术和参与OAEI 2012的前沿本体匹配系统.
6 总结本文建立了基于局部标准匹配结果的本体匹配问题的多目标优化模型,提出了基于局部标准匹配结果的度量方法,并进一步提出一种本体概念聚类算法以构建局部标准匹配结果. 在此基础上提出了一种基于局部标准匹配结果的MOEA/D算法的本体匹配方法,给出了用MOEA/D算法求解基于局部标准匹配结果的本体匹配多目标优化模型的详细步骤. 同基于遗传算法的本体匹配系统GOAL以及OAEI 2012参与者进行比较,结果表明基于本体概念聚类方法构建的局部标准匹配结果的MOEA/D算法可以找到比基于经典遗传算法的GOAL系统和前沿本体匹配系统更好的解.
| [1] | Noy N F, Musen M A. Algorithm and tool for automated ontology merging and alignment[C]//Proceedings of the 17th National Conference on Artificial Intelligence. Canada: Stanford University, 2000: 1-6. |
| [2] | Madhavan J, Bernstein P A, Rahm E. Generic schema matching with cupid[C]///Proceedings of the 27th International Conference on VLDB. Berlin, Germany: Springer, 2001: 49-58. |
| [3] | Noessner J, Niepert M. Codi: Combinatorial optimization for data integration-results for OAEI 2010[C]//Proceedings of the 27th ISWC 2010. Berlin, Germany: Springer, 2010: 142. |
| [4] | Chua W W K, Kim J J. Eff2Match results for OAEI 2010[C]//Proceedings of the ISWC 2010. Berlin, Germany: Springer, 2010: 150. |
| [5] | Wang Z C, Zhang X, Hou L, et al. RiMOM results for OAEI 2010[C]//Proceedings of the ISWC 2010. Berlin, Germany: Springer, 2010: 195. |
| [6] | Jean-Mary Y R, Shironoshita E P, Kabuka M R. Ontology matching with semantic verification[J]. Journal of Web Semantics, 2009, 7(3): 235-251. |
| [7] | Gracia J, Bernad J, Mena E. Ontology matching with CIDER: Evaluation report for OAEI 2011[C]//Proceedings of the 6th International Workshop on Ontology matching. Berlin, Germany: Springer, 2011: 126. |
| [8] | Hughes T C, Ashpole B C. The semantics of ontology alignment[R]. USA: Lockheed Martin Advanced Technology Lab, 2004. |
| [9] | Back T. Evolutionary algorithms in theory and practice: Evolution strategies, evolutionary programming, genetic algorithms[M]. Oxford, UK: Oxford University, 1996. |
| [10] | Holland J H. Adaptation in natural and artificial systems[M]. USA: University of Michigan, 1975. |
| [11] | Do H H, Rahm E. Matching large schemas: Approaches and evaluation[J]. Information Systems, 2007, 32(6): 857-885. |
| [12] | Hu W, Qu Y Z, Cheng G. Matching large ontologies: A divide-and-conquer approach[J]. Data and Knowledge Engineering, 2008, 67(1): 140-160. |
| [13] | Wang P, Xu B W. Lily: Ontology Alignment Results for OAEI 2008[C]//Proceedings of the 3rd International Workshop on Ontology Matching. Berlin, Germany: Springer, 2008: 167-175. |
| [14] | Kirsten T, Gross A, Hartung M, et al. GOMMA: A component-based infrastructure for managing and analyzing life science ontologies and their evolution[J]. Journal of Biomedical Semantics, 2011, 2(6): 1-8. |
| [15] | Guha S, Rastogi R, Shim K. ROCK: A robust clustering algorithm for categorical attributes[C]//Proceedings of the 15th International Conference on Data Engineering. Piscataway, NJ, USA: IEEE, 1999: 512-521. |
| [16] | Yuruk N, Mete M, Xu X, et al. AHSCAN: Agglomerative hierarchical structural clustering algorithm for networks[C]//International Conference on Advances in Social Network Analysis and Mining. Piscataway, NJ, USA: IEEE, 2009: 72-77. |
| [17] | Zhang Q F, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. |
| [18] | Stoilos G, Giorgos S, Stefanos K. A string metric for ontology alignment[C]//The Semantic Web-ISWC 2005. Berlin, Germany: Springer, 2005: 624-637. |
| [19] | Bechikh S, Said L B, Ghédira K. Searching for knee regions of the Pareto front using mobile reference points[J]. Soft Computing, 2011, 15(9): 1807-1823. |
| [20] | Deb K, Gupta S. Towards a link between knee solutions and preferred solution methodologies[M]//Swarm, Evolutionary, and Memetic Computing. Berlin, Germany: Springer, 2010: 182-189. |
| [21] | Fang K T. The uniform design: Application of number-theoretic methods in experimental design[J]. Acta Mathematicae Applicatae Sinica, 1980, 3(4): 363-372. |
| [22] | Wang Y, Fang K T. A note on uniform distribution and experimental design[J]. Science Bulletin, 1981, 26(6): 485-489. |
| [23] | Miller G A. WordNet: A lexical database for English[J]. Communications of the ACM, 1995, 38(11): 39-41. |
| [24] | Melnik S, Garcia-Molina H, Rahm E. Similarity flooding: A versatile graph matching algorithm and its application to schema matching[C]//18th International Conference on Data Engineering. Piscataway, NJ, USA: IEEE, 2002: 117-128. |
| [25] | Martinez-gil J, Alba E, Aldana-montes J F. Optimizing ontology alignments by using genetic algorithms[C]//Proceedings of the Workshop on Nature based Reasoning for the Semantic Web. Karlsruhe, Germany: University of Karlsruhe, 2008: 21-45. |



