2. 南京师范大学江苏省三维打印装备与制造重点实验室, 江苏 南京 210042
2. Jiangsu Key Laboratory for 3D Printing Equipment and Manufacturing, Nanjing Normal University, Nanjing 210042, China
1 引言
网络控制系统是集通信网络与控制于一体的分布式控制系统,是指某个区域现场传感器、 控制器、 执行器和通信网络的集合,用以提供设备之间的数据传输,使得区域内不同地点的用户实现资源共享和协作操作[1, 2, 3, 4]. 由于网络控制系统的规模庞大,网络节点失效的现象经常发生,这会降低系统性能甚至会导致系统不稳定. 近年来,网络控制系统的容错控制受到一定的关注. 如文[5]考虑传感器失效的问题,给出了在保证闭环T-S系统均方渐近稳定前提下状态反馈控制器的设计方法. 文[6]针对一类时变采样网络控制系统,提出了鲁棒容错控制的方法. 以上工作都属于周期采样控制的方法,从系统分析和设计角度看比较容易实现,但若考虑到通讯信道的带宽有限问题,周期采样方法有时就有一定的局限性. 如,在系统稳定的情况下,如果没有外界扰动施加于系统,还是周期地执行采样与通信任务,会浪费通讯资源,增加网络传输负载.
为克服周期采样控制方法的缺点,引入事件触发机制显得尤为重要. 所谓事件触发机制就是在保证闭环系统具有一定性能的情况下,一旦触发预先设计好的事件传送条件,控制任务即被执行. 目前,基于事件传送机制的研究已取得一些初步的成果[7, 8]. 针对一类线性系统,文[7]提出了一种离散的事件传送机制,建立了包含时变传输时延和事件传送机制的统一等效时滞模型. 考虑节点的随机故障,文[9]给出了基于事件触发机制的闭环系统指数均方稳定的充分条件. 文[10]将事件触发机制推广到非线性系统,利用李亚普诺夫泛函方法和线性矩阵不等式技术,联合设计事件触发机制和模糊控制器. 上述文献分别讨论了基于事件触发机制的线性系统容错控制、 非线性系统的事件触发机制控制,而针对基于事件触发机制的非线性系统的容错控制还没有得到充分研究.
T-S模糊系统的本质在于把一个非线性系统模型看成多个局部线性化模型的模糊逼近. 因此T-S模糊模型是非线性系统建模的一个重要工具. 在实际应用中,T-S模型系统一般都具有采样机制或经过网络进行传送. 文[11]考虑网络环境的影响,控制器的前件变量为μi(θ(k-τk)),其中τk表示网络诱导时延,而被控对象的前件变量为μi(θ(k)),这样就会造成前件变量的异步. 针对异步变量的问题,文[12]提出前件变量空间分割的方法. 文[13]通过零阶保持器的假设,其异步变量问题得到解决,但是由于T-S系统内存在规则间的非线性交互作用,所以很难得到较精确的离散化模型. 文[14]采用模糊李亚普诺夫泛函方法,通过引入自由变量给出了前件变量依赖型稳定的充分条件,而当系统的维数比较大时,所需计算资源会急剧增加.
针对网络资源受限的T-S模糊系统,本文引入离散化事件触发机制. 首先将网络诱导时延、 执行器故障和触发条件建立在统一的模型中; 然后考虑前件变量异步的情形,构造控制器与T-S系统前件变量间的关系. 通过构造的变量关系,采用李亚普诺夫泛函方法,得到闭环T-S系统的均方稳定条件,进一步给出事件传送策略和容错控制器协同设计方法.
2 系统描述在网络控制系统中,假设被控对象为如下T-S模糊系统:

定义θ(t)=[θ1(t),…,θg(t)]T. 采用单点模糊化、 乘积推理和平均加权反模糊化,T-S模糊系统总体模型可写为

 为模糊隶属度函数,
为模糊隶属度函数,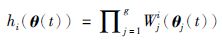 为第i条模糊规则的权重,Wji(θj(t))表示θj(t)在模糊集Wji中的隶属度.
为第i条模糊规则的权重,Wji(θj(t))表示θj(t)在模糊集Wji中的隶属度.
假设被控对象的所有状态变量都是可测的. 传感器是时钟驱动的,控制器是事件驱动的,执行器为具有零阶保持器的事件驱动结构. 数据包单包传送且不存在丢包现象,网络诱导时延τk为区间时变时延,满足τk∈[τmin,τmax],τmin、 τmax为非负实数.
针对执行器失效这一故障,基于文[5]所描述的随机传感器故障模型,建立随机执行器故障模型:
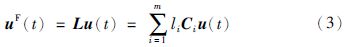

为减少网络中的数据传输量,降低网络负载压力,不同于通常研究的网络控制系统[15],在本文所研究的网络控制系统中,传感器与控制器之间装有一个事件发生器,事件发生器根据事先设定好的事件触发条件对接收到的采样数据进行筛选,符合触发条件的采样信号即被释放,经过网络传送给控制器,否则不释放. 假设最新传输出去的数据为x(tkh),对应的发送时刻为tkh,h为采样周期,则下次释放数据的时刻为

注1 释放时刻{t0h,t1h,t2h,…}是采样时刻{0,h,2h,…}的子集. 只有部分采样数据通过网络进行传输,说明所提出的事件触发机制能够节省网络带宽资源,减少控制器的计算次数. 特别地,当σ=0时,{t0h,t1h,t2h,…}={0,h,2h,…},即事件触发机制(5)退化为通常的周期传送策略. 另外,传输时刻{t0h,t1h,t2h,…}不仅依赖于参数σ,而且依赖于当前系统状态. 因此,本文提出的事件触发机制属于状态依赖型触发机制.
对于式(1)所述的T-S模型,利用传统的并行分布补偿原理设计模糊控制器是一种简便有效的方法. 考虑事件触发机制和网络诱导时延的作用,其相应的模糊控制器为
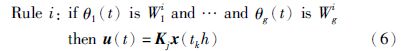

结合式(2)、 (3)和式(7),当t∈Ω时,实际的闭环控制系统可表示为
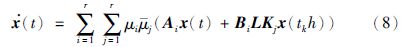
注2 式(8)中前提变量项μij并不是一个对称结构,因为μij≠μji,故在推导中不能进行等效转化,也就是闭环T-S模糊系统中存在前件变量异步的问题[16].
针对上述的异步前件变量问题,类似文[17],假设存在实数ρj、 Δj使得下式成立:
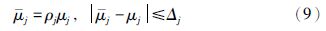
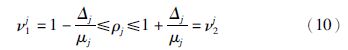
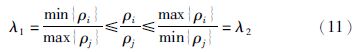
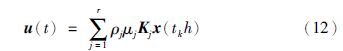
注3 当式(11)中的λ1=λ2=1时,ρi=ρj=ρ,即j=ρμj. 根据前提变量的性质,可以得到
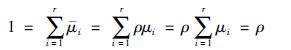
考虑j=ρjμj,当t∈Ω时,闭环系统(8)可转化为
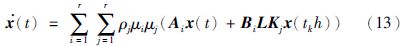
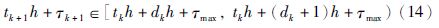
由式(14)可以推得区间Ω可划分为dk个子区间:
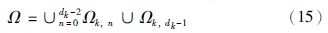
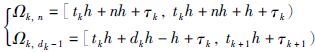 .
.
定义η(t)=t-tknh. 在每个区间Ωk,n上,都有:

通过上述分析,闭环系统(13)可以等价表示为
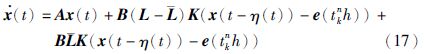
 .
.
由于系统(17)中含有随机变量L,分析方法也要作相应的改变,首先引入如下的定义[16]:
定义1 对给定的函数V: CF0b([-η2,0),Rn)×S,其无穷小算子l被定义为
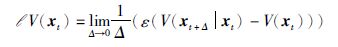
下面将给出闭环T-S系统(17)的稳定条件,然后利用这一条件给出容错控制器设计的方法. 为研究其稳定性问题,构建如下候选的李亚普诺夫泛函:

定理1 给定标量η1、 η2、 σ、 λ1、 λ2和矩阵Kj(j=1,2,…,r),假如存在具有适当维数的P>0、 Qi>0、 Ri>0(i=1,2)、 Φ>0和U,使得下列线性矩阵不等式成立(l,i,j=1,2,…,r,i <j):

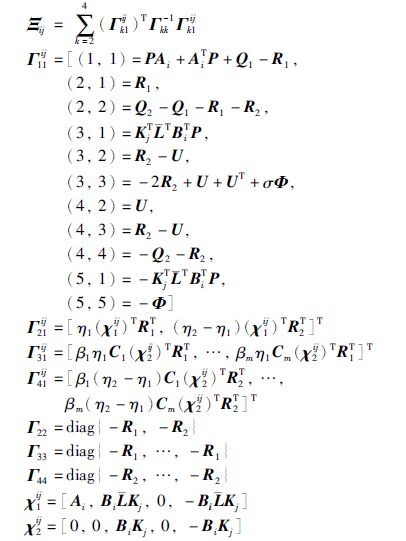
证明 对式(18)中的V(t)使用无穷小算子式并对取其期望值,可以得到

根据Jensen不等式[19]和Reciprocally convex方法[20],存在U满足式(20),使下列不等式成立:
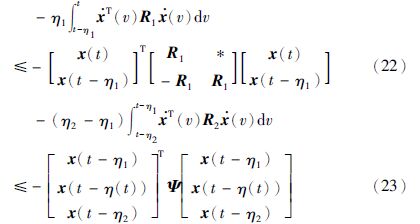
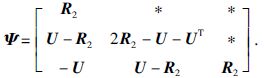
根据式(4),可以得到
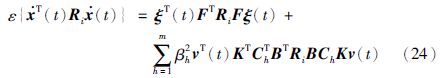

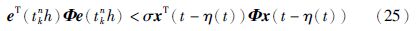
结合式(21)~(25),下式明显成立:

由于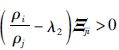 ,式(19)保证:
,式(19)保证:

另外根据式(11),可以得到

结合式(26)~(28),容易得到ε{lV(t)}<0. 由于∪k=0∞∪n=0dk-1Ωk,n=[t0,∞),容易得到系统(17)在整个定义区间上是均方渐近稳定的.
基于定理1,下面给出系统(1)容错控制器设计的方法.
定理2 给定标量η1、 η2、 σ、 λ1和λ2,假如存在具有适当维数的X>0、 ${\tilde Q}$i>0、 i>0(i=1,2)、 ${\tilde R}$>0、 ${\tilde U}$>0和Yj(j=1,2,…,r),使得下列矩阵不等式成立(l,i,j=1,2,…,r,i <j):
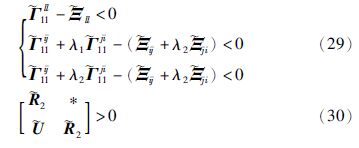
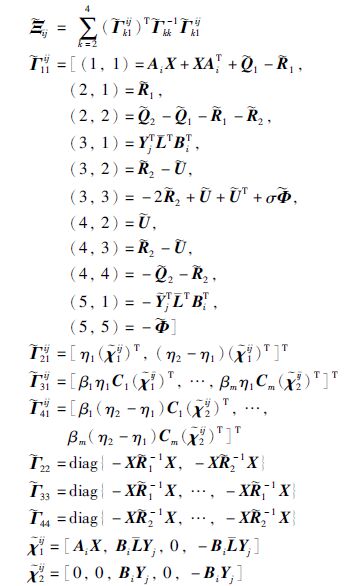
证明 定义X=P-1,Yj=KjX,XΦX=,XQiX=i(i=1,2),XRiX=i(i=1,2),XUX=. 分别用diag{X,X,X,X,X},diag{X,X}及它们的转置矩阵左乘、 右乘式(19)和式(20),代入相应的定义符号,可得式(29)和式(30).
注4 定理2说明了基于事件触发机制的网络化T-S模糊系统的容错控制问题是可解的. 本文给出的方法相比文[10]有以下3个优点: 首先,考虑了执行器失效这一常见的随机故障,在保证系统稳定的前提下给出了容错控制器的设计方法; 其次,在证明过程中,文[10]利用的是传统的自由权矩阵方法,需要引入41n2+5n2个决策变量,而采用本文的Reciprocally convex技术只引入了7n2+5n2个变量,因此本文方法有较好的计算能力,能够节约计算资源; 最后,在稳定性分析和控制器综合时考虑了T-S系统中前提变量的异步问题. 若不考虑变量关系(9),可以得到类似文[11]的结果.
推论1 给定标量η1、 η2和σ,假如存在具有适当维数的X>0、 ${\tilde Q}$i>0、 ${\tilde R}$i>0(i=1,2)、 ${\tilde \Phi }$>0、 ${\tilde U}$>0和Yj(j=1,2,…,r),使得式(30)和下列矩阵不等式成立(i,j=1,2,…,r):

注5 由于存在非线性项Xi-1X(i=1,2),定理2及推论1不能直接利用Matlab中LMI工具箱进行求解. 文[5, 11]详述了锥补线性化方法,本文就不再赘述.
4 仿真例子考虑具有如下参数的系统:
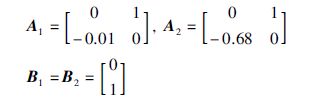
给定系统初始状态x(0)=[2, -1]T,隶属度函数为
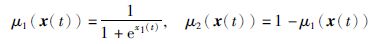
下面将分3种情况来讨论模糊控制器及事件触发机制的设计.
情况1 不考虑执行器的随机故障和事件触发机制,即α=1,β=0,σ=0. 表 1给出了不同的λ1、 λ2,系统稳定所允许的最大延迟上界η2和控制器增益K1、 K2. 由表 1可明显看出,利用推论1求得的控制器是线性控制器,而利用定理2能够得到非同增益的模糊控制器. 另外定理2增加了保证系统稳定前提下的最大允许时延上界,相比推论1降低了保守性. 当模糊控制器的前件变量与被控对象保持一致时,即不考虑通信网络的影响情况下所得结果的保守性最低.
| λ1,λ2 | η2 | K1,K2 | |
| 推论1 | -,- | 0.701 | 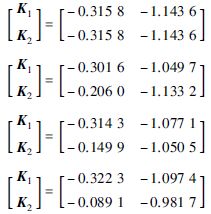
|
| 定理2 | 0.8,1.25 | 0.701 | |
| 0.9,1.11 | 0.742 | ||
| 1,1 | 0.783 |
情况2 当不考虑执行器的故障时,令η1=0,λ1=λ2=1,表 2给出了不同的σ求得的最大时延η2及相应的控制器增益K1、 K2、 事件触发机制参数Φ. 若不考虑网络延迟,因为η2=h+τM,所以最大可容许的采样周期h分别为0.7、 0.5、 0.4、 0.4、 0.3. 利用表 2中数据,在仿真时间t∈[0, 28]中,传感器发送数据占采样数据的100%、 77.19%、 71.83%、 61.97%、 48.94%,事件触发机制有效节约22.81%、 28.17%、 38.03%、 51.06%的通讯资源. 可以看出,参数σ越大,数据发送百分比p%越小,所得/h越大,其中表示平均采样周期.
| σ=0 | σ=0.1 | σ=0.2 | σ=0.3 | |
| η2 | 0.7 | 0.5 | 0.4 | 0.4 |
| K1 | [-0.428 9 -1.175] | [-0.430 2 -1.149 4] | [-0.474 0 -1.274 7] | [-0.454 4 -1.447 4] |
| K2 | [-0.134 5 -0.861 6] | [-0.115 1 -0.948 2] | [-0.147 4 -1.049 6] | [-0.164 4 -1.368 1] |
| Φ | - | 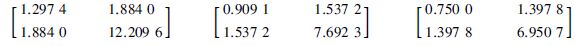
| ||
| p% | 41/41 | 44/57 | 51/71 | 44/71 |
| /h | 1 | 1.295 5 | 1.392 2 | 1.613 6 |
情况3 当执行器发生故障(α=0.5,β=0.5)时,取σ=0.1,η1=0.05,λ1=0.8和λ2=1.25,应用定理2,得到η2的上界是0.44,相应的控制器增益K1、 K2和事件传送策略矩阵Φ分别为

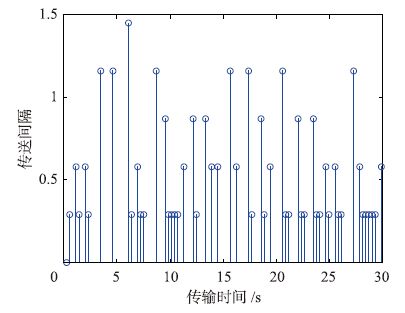
这里假设网络传输时延τk∈[0.05,0.15],则最大采样周期为h=0.19. 在考虑网络传输延时及执行器故障的情况下,利用上述参数,在仿真时间[0, 30]中,只有占总采样数据的52.88%的数据包通过网络发送给控制器. 图 1描绘了在同时考虑事件传送策略,执行器故障和网络诱导延迟时系统的状态响应曲线. 图 2描绘了传送时刻及相邻传送时刻的间隔. 可以看出,利用本文设计的事件传送策略和容错控制器,在保证一类闭环T-S模糊系统稳定的前提下,不仅能够减少网络通讯信道的数据量,而且能够使得系统对执行器故障和网络诱导延迟具有一定的鲁棒性.

|
| 图 1 系统状态响应 Fig. 1 System state responses |
|
| 图 2 传送时刻及相邻传送时刻的间隔 Fig. 2 Release time and interval of neighbouring release time |
针对一类由T-S模糊系统描述的非线性系统,讨论了事件触发机制的设计和容错控制的问题. 首先在考虑网络诱导时延,执行器随机故障和异步前件变量的情况下,构建了统一的闭环T-S模糊系统模型. 然后利用时滞系统方法,研究了等效T-S系统的均方渐近稳定性问题,并给出了容错控制器的设计方法. 与已有的线性化结果相比,由于前件变量异步条件的引入,所得结果保守性较小. 实例说明了本文设计的事件触发机制和容错控制器不仅能够减少网络负载压力,而且能够使系统具有一定的鲁棒性能.
| [1] | Yang T C. Networked control system: A brief survey[J]. IEE Proceedings: Control Theory and Applications, 2006, 153(4): 403-412. |
| [2] | 游科友, 谢立华. 网络控制系统的最新研究综述[J]. 自动化学报, 2013, 39(2): 101-118. You K Y, Xie L H. Survey of recent progress in networked control systems[J]. Acta Automatica Sinica, 2013, 39(2): 101-118. |
| [3] | 胡豪立, 邵奇可. 资源约束网络控制系统的非均匀采样控制[J]. 信息与控制, 2013, 42(3): 320-326. Hu H L, Shao Q K. Non-uniformly sampling control of networked control systems with communication constraints[J]. Information and Control, 2013, 42(2): 320-326. |
| [4] | 芮方智, 江汉红, 侯重远. 网络控制系统研究与展望[J]. 信息与控制, 2012, 41(1): 83-88. Rui F Z, Jiang H H, Hou C Y. Survey and prospect of networked control system[J]. Information and Control, 2012, 41(1): 83-88. |
| [5] | Peng C, Fei M R, Tian E. Networked control for a class of T-S fuzzy systems with stochastic sensor faults[J]. Fuzzy Sets and Systems, 2013, 212(1): 62-77. |
| [6] | 黎煊, 吴晓蓓, 王玉龙, 等. 时变采样周期网络控制系统的鲁棒容错控制器设计[J]. 控制与决策, 2009, 24(12): 1890-1894. Li X, Wu X B, Wang Y L, et al. Robust fault-tolerant controller design of networked control systems under variable-period sampling[J]. Control and Decision, 2009, 24(12): 1890-1894. |
| [7] | Yue D, Tian E, Han Q L. A delay system method for designing event-triggered controllers of networked control systems[J]. IEEE Transactions on Automatic Control, 2013, 58(2): 475-481. |
| [8] | Meng X, Chen T. Event triggered robust filter design for discrete-time systems[J]. IET Control Theory and Applications, 2014, 8(2): 104-113. |
| [9] | Liu J, Yue D. Event-triggering in networked systems with probabilistic sensor and actuator faults[J]. Information Sciences, 2013, 240(1): 145-160. |
| [10] | Peng C, Han Q L, Yue D. To transmit or not to transmit: A discrete event-triggered communication scheme for networked T-S fuzzy systems[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(1): 164-170. |
| [11] | Hu S, Zhang Y, Yin X, et al. T-S fuzzy-model-based robust stabilization for a class of nonlinear discrete-time networked control systems[J]. Nonlinear Analysis: Hybrid Systems, 2013, 8(1): 69-82. |
| [12] | Zhang C, Feng G, Gao H, et al. H∞ filtering for nonlinear discrete-time systems subject to quantization and packet dropouts[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(2): 353-365. |
| [13] | Koo G B, Park J B, Joo Y H. Intelligent digital redesign for nonlinear systems using a guaranteed cost control method[J]. International Journal of Control, Automation and Systems, 2013, 11(6): 1075-1083. |
| [14] | Lam H K, Lauber J. Membership-function-dependent stability analysis of fuzzy-model-based control systems using fuzzy Lyapunov functions[J]. Information Sciences, 2013, 232(1): 253-266. |
| [15] | 宋洪波, 俞立, 张文安. 存在通信约束和时延的多输入多输出网络控制系统镇定研究[J]. 信息与控制, 2007, 36(3): 334-339.Song H B, Yu L, Zhang W A. Stabilization of MIMO networked control systems with communication constraints and delays[J]. Information and Control, 2007, 36(3): 334-339. |
| [16] | Lee H J. Comments on “T-S fuzzy-model-based robust design for networked control systems with uncertainties”[J]. IEEE Transactions on Industrial Informatics, 2009, 5(4): 507-507. |
| [17] | Peng C, Yue D, Fei M. Relaxed stability and stabilization conditions of networked fuzzy control systems subject to asynchronous grades of membership[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(5): 1101-1112. |
| [18] | Tian E, Yue D. Reliable H∞ filter design for T-S fuzzy model-based networked control systems with random sensor failure[J]. International Journal of Robust and Nonlinear Control, 2013, 23(1): 15-32. |
| [19] | Gu K, Chen J, Kharitonov V L. Stability of time-delay systems[M]. Berlin, Germany: Springer-Verlag, 2003: 147-195. |
| [20] | Park P G, Ko J W, Jeong C. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47(1): 235-238. |



