1 引言
烟气轮机是一种将化工过程再生烟气中所具有的热能和动能通过膨胀做功转变为机械能的大型高转速透平机械,其主要功能是给装置再生系统供风或驱动发电机发电,以达到能量回收的目的[1]. 由于长期运行在高温高压、 高冲蚀、 高转速等特殊环境下,烟机很难达到理想的运行状态,常常会出现高振值、 刮瓦、 自保联锁误动作等故障,从而导致机组停车甚至转子叶片损坏、 联轴器断裂等恶性事故. 在实际应用中常常需要频繁地停机检查以保证烟机的安全运行,这不仅导致烟机的工作效率低下,而且对人身安全和企业的经济效益都造成了严重影响. 因此,保证烟机安全、 平稳、 优质、 长期的运行就显得尤为重要. 当前有关烟机运行状态的研究大多集中在过程监测[2]、 故障诊断[3]等领域,取得了一定成果,但这些研究并不能从本质上解决烟机连续稳定运行的问题. 如果能通过对烟机运行状态的潜在风险进行预估判断来决定是否需要对烟机进行重点监测或全面检查,就能在故障未发生时提前做出应对措施,避免大量不必要的停机检查操作,有效提高烟机的工作效率,从而保证烟机长时间稳定高效运行.
在风险预估识别与评价领域中,层次分析法(AHP)[4, 5]、 模糊综合评价法[6, 7]、 灰色理论评价法[8, 9]、 人工神经网络法(ANN)[10, 11]等都有着广泛的应用. 然而,这些方法都存在着各种各样的限制和不足. 比如,AHP方法和模糊综合评价方法,必须要求使用经验知识来确定模糊规则和各指标的权重,不可避免地会受到人为因素影响. 灰色理论通过对少量模糊、 不完整、 无规律的原始数据进行关联分析,寻找隐藏的规律建立模型进行预测,但灰色评价理论必须先确定灰色问题的白化函数,而该函数的选取目前多由人工确定,实际中不易获得. 人工神经网络方法虽然可以直接从训练样本中获得知识克服人为因素造成的主观影响,但也存在训练速度慢,网络参数难以确定的问题.
可拓神经网络(extension neural network,ENN)[12]是继模糊神经网络、 遗传神经网络、 进化神经网络之后的又一种新型的网络类型,对解决那些需要识别和分类的对象所对应的特征值在区间内变化的问题效果显著. 由于具有结构简单、 物理意义明确、 训练速度快等优势,ENN已经获得了不少成功的应用[13, 14, 15]. 文[13]将ENN与交通灯的智能控制相结合,取得了不错的效果; 文[14]将ENN应用到煤矿安全监控领域,成功地对煤矿运行的风险等级进行预测,具有较好的经济价值; 文[15]从样本选择的角度对ENN加以改进,提高了ENN的性能. 但上述方法中ENN的参数通常是根据经验人为设置的,需要通过反复的测试来寻找最优参数,不仅需要耗费大量时间和人力,而且也不能保证达到最佳的预测效果,这极大地限制了ENN的适用范围.
差分进化(differential evolution,DE)[16]是一种新兴的进化计算方法,与其它算法(如遗传算法、 粒子群算法等)相比,具有原理简单、 容易实现、 受控参数较少、 鲁棒性好等优点[17, 18, 19]. 本文在ENN的基础上,将差分进化思想引入到ENN中,提出了一种基于差分进化—可拓神经网络(DE-ENN)的风险识别方法,通过动态自适应地优化加权系数和学习速率来获得最佳的预测结果. 最后将其应用到烟机的运行状态潜在风险识别中,取得了较理想的效果.
2 ENN学习算法ENN属于双层双权值结构,包括输入层、 输出层和连接两层之间的权值,基本结构如图 1所示. 其中,xijp为类别p对应的第i个样本的第j个输入,Oik为第i个输入对应的第k个输出,ωkjL和ωUkj表示第j个输入和第k个输出之间的连接权值,n和nc分别表示输入和输出节点数.

|
| 图 1 ENN的基本结构图 Fig. 1 Schematic structure of extension neural network |
ENN区别于其它传统分类神经网络的地方在于: 用可拓距离代替欧氏距离作为测量样本和类中心的距离函数. 欧氏距离一般表示点与点的距离,而可拓距离则将其拓展到点与区间的距离. 可拓距离表示如下:
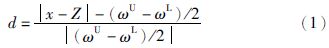
d表示x与区间〈ωL,ωU〉的可拓距离,其函数关系如图 2所示. 从图 2中可以看到可拓距离的变化率与区间的大小成反比,区间越小,可拓距离的变化量就越大. 对于较小的区间,当x与其相对位置发生微小变化时,可拓距离会发生几倍甚至几十倍的变化,无形中放大了特征样本之间的差异. 这种对小区间样本较强的敏感性应用到分类上,尤其是基于小区间范畴的分类识别是一个突出的优势.

|
| 图 2 可拓距离 Fig. 2 Extension distance |
ENN的学习机制属于有监督学习,学习的目的是对ENN的网络权值和类中心进行调整来获得更好的分类效果或使分类误差达到最小. ENN的学习算法描述如下:
假设训练样本集为X={X1,X2,…,XNp},Np是样本数. 第i个样本是Xip={Xi1p,Xi2p,…,Xijp,…,Xinp},n是样本特征总数,p为对应的类别.
首先,利用可拓理论分析出样本的物元模型,确定初始权值及类中心. 接着输入第i个训练样本及对应类别p,计算训练样本Xip和第k类的可拓距离Dik:

然后,确定k*,使得Dik*=min{Dik}. 如果k*=p,计算下一个样本的可拓距离,否则调整第p类和第k*类的类中心和权值,如式(3)~(8).
(1) 调整类中心:

(2) 调整权值:


|
| 图 3 训练前后可拓距离的变化 Fig. 3 Changes of the extension distance before and after the training |
差分进化(DE)是一种基于群体差异的启发式随机搜索算法,其独特之处在于变异算子采用差分策略,利用种群中个体之间的差异对个体进行扰动,来实现个体变异. 本文在ENN的基础上,在可拓距离中引入权系数,对特征量的重要性程度进行量化处理,然后在训练时间最小和错误率最小的约束条件下,使用差分进化对加权系数和学习速率进行实时动态优化. 下面给出DE-ENN算法:
(1) 整理样本,确定特征向量以及风险类别. 为评价分类性能,定义错误率ET:

(2) 构建样本的物元模型,并初始化连接权值和类中心. 物元模型表示如下:

权值和类中心的初始化公式如下:


(3) 输入第i个训练样本及其所对应的类别p:

(4) 计算训练样本xijp和第k类的可拓距离:

(5) 调整权值和类中心. 确定k*,使得Dik*=min{Dik}. 如果k*=p,则直接跳转下一步,否则,按式(3)~(8)调整第p类和第k*类的类中心和权值.
(6) 重复步骤(3)~(5),如果所有的样本都已完成训练,那么一个训练步长结束,训练步长用Eepoch表示.
(7) 若错误率达到给定值或所有样本训练完成,则执行下一步,否则跳转步骤(3).
(8) 优化加权系数λj和学习速率η. 为了方便编码,令η=λ0. DE对λi(j=0,1,…,n)的优化过程如下:
1) 确定优化指标f:

2) 初始化种群. 初始种群可以表示为{λi(0)λj,iL≤λj,i(0)≤λj,iU},i=1,2,…,Q,j=1,2,…,m. 随机生成公式为
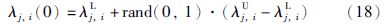
3) 变异算子. 随机选取种群中不同个体,对其向量差进行处理,然后与待变异个体进行向量合成,即:

要使解有效,必须判断个体中各“基因”是否满足条件,如果不满足,则重新随机生成. 第g代种群{λi(g)λj,iL≤λj,i(g)≤λj,iU}通过变异后,产生一个中间体:

4) 交叉算子. 对第g代种群λi(g)及其变异的中间体vi(g+1)进行个体间的交叉操作:

5) 选择算子. 采用贪心算法来选择下一代个体:

6) 重新执行步骤(3)~(5),得到新的ET和Eepoch,也即得到新的f.
7)反复进行步骤1)~7),直至f最小或者稳定.
(9) 若f符合要求,则结束; 否则重新执行步骤(8).
4 仿真测试为了验证DE-ENN的有效性,选取UCI(University of California Irvine)标准数据库中的Iris数据集和Wine数据集进行测试,并与误差反向传播(error back propagation,BP)算法、 学习向量量化(learning vector quantization,LVQ)算法及标准ENN算法进行对比. 仿真测试所需要的训练样本和测试样本均按比例随机生成,见表 1. 本文根据交叉验证方法选取DE的参数,其中交叉因子CR=0.5,缩放因子F=1. BP、 LVQ和ENN的学习速率分别取0.5、 0.01和0.1. 仿真结果如图 4所示.
| 实验类型 | 样本总数 | 训练样本 | 测试样本 | 输入变量 | 输出变量 |
| Iris | 150 | 75 | 75 | 4 | 3 |
| Wine | 178 | 120 | 58 | 13 | 3 |

|
| 图 4 数据测试结果 Fig. 4 Test results of data sets |
从图 4中可以看出,BP算法错误数分别为3个和4个,LVQ的错误数分别为2个和4个,ENN分别为1个和3个,而DE-ENN算法在Iris和Wine测试时识别错误数均为1个. 可以看出,DE-ENN在预测准确率上要明显优于BP和LVQ,同时对于较为复杂的Wine数据集,相比标准ENN,DE-ENN同样具有更好的识别结果.
为进一步验证算法的预测性能以及泛化能力,本文采用10折交叉验证方法继续实验,并重复10次实验取结果的平均值,具体结果见表 2. 从表 2可以看出,相比BP和LVQ,DE-ENN的结构更为简单,训练时间更短,训练错误率也更低,同时在预测结果上也具有较大优势. 与ENN相比,DE-ENN在学习时间上分别增加了2.8 s和4.4 s,但训练错误率却明显下降,同时预测结果也更加精确,表明DE-ENN不仅继承了ENN结构简单、 训练高效的优点,而且预测准确率也有了较大幅度提高. 同时,这也表明DE-ENN具有较强的泛化能力.
| 实验项目 | 算法 | 网络结构 | 参数设定 | 初始权值 | 连接权数目 | 平均学习时间 /s | 平均迭代次数 | 训练错误率 /% | 平均识别准确率 /% |
| Iris测试 | BP | 4-10-3 | 0.5(学习速率) | 在小区间内随机生成 | 70 | 12.5 | 225 | 11.23 | 95.32 |
| LVQ | 4-15-3 | 0.02(学习速率) | 在小区间内随机生成 | 105 | 8.4 | 24.3 | 8.25 | 93.77 | |
| ENN | 4-3 | 0.1 | 特征量的上下限 | 24 | 1.9 | 2 | 0 | 96.3 | |
| DE-ENN | 4-3 | DE优化得到 | 特征量的上下限 | 24 | 4.7 | 2 | 0 | 98 | |
| Wine测试 | BP | 13-10-8-3 | 0.8(学习速率) | 在小区间内随机生成 | 234 | 15.9 | >1 000 | 17.28 | 93.1 |
| LVQ | 13-18-3 | 0.05(学习速率) | 在小区间内随机生成 | 288 | 11.7 | 44.7 | 15.09 | 90.5 | |
| ENN | 13-3 | 0.2 | 特征量的上下限 | 78 | 2.5 | 4 | 8 | 93.7 | |
| DE-ENN | 13-3 | DE优化得到 | 特征量的上下限 | 78 | 6.9 | 4 | 0 | 96.55 |
本文以某炼化企业催化裂化装置中的国产YL型双极烟机为背景,进行运行状态的潜在风险识别. 烟机是催化裂化装置中能量回收系统的关键设备,其正常运行时的系统流程图如图 5所示. 从图 5可以看出,正常生产时,空气经过滤器进入3#主风机组,压缩后通过单向阀送往再生器对催化剂进行流化烧焦,焦化的催化剂经管道和原料油混合发生反应,而烧焦过程产生的高温烟气经由各个分离器进行连续分离,脱除其中混有的催化剂,然后送入烟机,推动烟机叶轮做功,带动风机和电机转动,从而减轻电机负担,降低电能消耗,达到能量回收利用的目的.

|
| 图 5 烟机运行的系统流程图 Fig. 5 The system flow chart of the flue gas turbine |
烟机运行模型的构建,关键在于特征量的选取. 考虑到烟机属于动力类设备,应该突出考虑动态指标,本文选择4个有代表性的动态特征作为运行模型的特征向量: 振动、 位移、 转速、 温度. 然后确定潜在风险状况为: 高(Ⅰ)、 中(Ⅱ)、 较低(Ⅲ)、 低(Ⅳ)四个等级. 当风险等级为高时,需要停机对烟机及其相关设备进行全面检修; 当风险等级为中时,需要对烟机个别部分重点关注; 当风险等级为较低和低时只需要保持时刻监视即可. 在进行潜在风险识别前需要先对现场采集到的各类特征数据进行预处理,得到标准化的评判指标Ci. 预处理公式如下:
1) 只有下限值:

2)只有上限值:

3)有上限、 下限值:

其中,Ci*为现场采集的实际数据,Cimin为数据采集点的给定下限值,Cimax为数据采集点的给定上限值.
由于烟机运行状态的潜在风险数据需要取自于不同的风险阶段,难以实时获取,文中以文[20]中的数据为例来说明该风险识别方法. 首先对数据进行分析,可以确定烟机运行模型的特征向量为C=[c1,c2,c3,c4],其中,振动c1、 位移c2、 转速c3、 温度c4; 接着利用可拓分析方法构建烟机运行的物元模型,并确定初始类中心和权值,接下来用DE-ENN算法对数据进行训练; 最后进行测试.
在进行数据测试时,本文从各风险等级对应的样本中各选取2组数据作为测试样本. 然后将该方法与现有的方法进行比较,为了保证效果,各个方法采用相同的训练样本和测试样本,测试10次,然后取平均值,最终结果见表 3. 其中,Elman网络的反馈增益因子取0.3,LVQ、 BP和ENN的学习速率分别取0.05、 0.02和0.1,DE-ENN方法中交叉因子的取值为CR=0.3,缩放因子F=1.2.
| 基本方法 | 结构 | 权值数量 | 平均学习时间 /s | 平均迭代次数 | 训练错误率 /% | 平均预测准确率 /% |
| Elman | 4-15-4 | 120 | 19.7 | >1 000 | >1 | 100 |
| LVQ | 4-15-4 | 120 | 11.3 | 28.6 | 0 | 100 |
| BP | 4-9-4 | 72 | 14.5 | 243.8 | 1.2 | 97.5 |
| ENN | 4-4 | 32 | 1.6 | 1.1 | 12.9 | 91.7 |
| DE-ENN | 4-4 | 32 | 4.2 | 2 | 0 | 100 |
从表 3中可以看出,在预测准确率方面,基于DE-ENN的方法和其他方法如Elman方法、 LVQ方法、 BP神经网络以及标准ENN效果差别不大,都能有较好的预测效果. 但是在迭代次数上,Elman方法的迭代次数最多,超过1 000次,而LVQ和BP方法也分别为28.6次和243.8次,DE-ENN的迭代次数仅为2次,这大大简化了算法的执行过程. 在训练时间上,DE-ENN算法只需要4.2 s即可完成,相比Elman、 LVQ和BP,具有较大的优势; 虽然在这些方法中,ENN用时最短,但DE-ENN在训练时间仅增加了2.6 s的情况下,训练错误率降低了12.9%,预测准确率提高了8.3%. 这表明,相比于其他方法,DE-ENN的结构更为简单,训练过程更为高效,预测结果也更加精确. 与此同时,DE-ENN的特征值分类边界一开始就被清晰的界定,即训练前就获得了比较专业的知识,这就使得该方法对于新的和重要的数据信息有着很强的适应性,能通过获取其中的知识来不断完善自身的预测分类性能.
6 结论本文提出了一种新的基于DE-ENN的烟气轮机运行风险识别算法. 首先对烟机运行状况的潜在风险进行分析,然后详细介绍了DE-ENN算法,最后以某炼化企业的烟机为例,运用该方法进行预测识别,并将结果与其它各类方法进行比较. 最终结果表明,该方法对烟机的潜在风险识别是有效的,并且相比于其它方法,DE-ENN的结构简单清晰、 参数意义明确,具有更为高效的训练过程和更优异的预测能力.
| [1] | Ji H A, Sung K P, Tong S K. Influence of gas turbine specification and integration option on the performance of integrated gasification solid oxide fuel cell/gas turbine systems with CO2 capture[J]. Journal of Mechanical Science and Technology, 2013, 27(9): 2845-2856. |
| [2] | 王业坚. 烟机状态监测与叶片结垢分析研究[D], 大庆: 大庆石油学院, 2008. Wang Y J. Research on condition monitor and blade dust deposit for flue gas turbine[D]. Daqing: Daqing Petroleum Institute, 2008. |
| [3] | Silvio S. Identification and fault diagnosis of a simulated model of an industrial gas turbine[J]. IEEE Transactions on Industrial Informatics, 2005, 1(3): 202-216. |
| [4] | Ahsan M K, Bartlema J. Monitoring healthcare performance by analytic hierarchy process: A development-country perspective[J]. International Transactions in Operational Research, 2004, 11(4): 465-478. |
| [5] | 陈桥, 胡克, 雒昆利, 等. 基于AHP法的矿山生态环境综合评价模式研究[J]. 中国矿业大学学报, 2006, 35(3): 377-383. Chen Q, Hu K, Luo K L, et al. Study on the synthetical assessment model of mine eco environments based on AHP[J]. Journal of China University of Mining & Technology, 2006, 35(3): 377-383. |
| [6] | Su Y, Zhao H, Su W J, et al. Fault assessment/diagnosis based on fuzzy expert system[J]. Journal of Northeastern University: Natural Science, 2004, 25(7): 653-656. |
| [7] | Zou Q, Zhou J Z, Zhou C, et al. Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP[J]. Stochastic Environmental Research and Risk Assessment, 2013, 27(2): 525-546. |
| [8] | 施冬, 陈军, 朱庆. 基于GIS的油气层灰色综合评价研究[J]. 地球物理学进展, 2005, 20(l): 83-88. Shi D, Chen J, Zhu Q. GIS based grey comprehensive evaluation on oil gas reservoir[J]. Progress of Geophysics, 2005, 20(1): 83-88. |
| [9] | 张识宇, 李大建, 杨乃定. 基于综合赋权的风险企业增值潜力灰色评价方法[J]. 控制与决策, 2008, 23(10): 1122-1128. Zhang S Y, Li D J, Yang N D. Grey comprehensive evaluation on value added potential of venture business based on combination weighting[J]. Control and Decision, 2008, 23(10): 1122-1128. |
| [10] | Sun G, Zhang R X, Luo F. Evaluation method of coal mine production safety based on BP neural network [C]//Proceedings of the 2009 International Conference on Information Technology and Computer Science. Piscataway, NJ, USA: IEEE, 2009: 514-517. |
| [11] | Victor L M, Ricardo C S, Ahda P G P, et al. Artificial neural network based approach for anti-islanding protection of distributed generators[J]. Journal of Control, Automation and Electrical Systems, 2014, 25(3): 339-348. |
| [12] | Wang M H, Hung C P. Extension neural network and its applications[J]. Neural Networks, 2003, 16(5): 779-784. |
| [13] | Chao K H, Lee R H, Wang M H. An intelligent traffic light control based on extension neural network[M]//Lecture Notes in Computer Science: vol. 5177. Berlin, Germany: Springer-Verlag, 2008: 17-24. |
| [14] | Zhou Y, Pedrycz W, Qian X. Application of extension neural network to safety status pattern recognition of coal mines[J]. Journal of Central South University of Technology, 2011, 18(3): 633-641. |
| [15] | 周玉, 钱旭, 王自强. 基于阴影集数据选择的可拓神经网络性能改进[J]. 北京工业大学学报, 2013, 39(3): 430-437. Zhou Y, Qian X, Wang Z Q. Performance improvement of extension neural network using data selection method based on shadowed sets[J]. Journal of Beijing University Technology, 2013, 39(3): 430-437. |
| [16] | Storn R, Price K. Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[R]. Berkeley, USA: University of Californi, 1995. |
| [17] | 刘波, 王凌, 金以慧. 差分进化算法研究进展[J]. 控制与决策, 2008, 22(7): 721-729. Liu B, Wang L, Jin Y H. Advances in differential evolution[J]. Control and Decision, 2008, 22(7): 721-729. |
| [18] | Joes C V T, Carlos A C C. hypDE: A hyper-heuristic based on differential evolution for solving constrained optimization problems [M]//Advances in Intelligent Systems and Computing: vol. 175. Berlin, Germany: Springer-Verlag, 2013: 267-282. |
| [19] | 李维刚, 贾树晋, 郭朝晖. 基于分解的多目标差分进化算法及其应用[J]. 信息与控制, 2013, 42(3): 392-400. Li W G, Jia S J, Guo C H. A multi-objective differential evolution algorithm based on decomposition and its application[J]. Information and Control, 2013, 42(3): 392-400. |
| [20] | 冯显富, 基于混沌理论的石油炼化企业风险预控技术研究[D]. 北京: 中国地质大学, 2010. Feng X F. A study on the theories and methods of the production safety risk early-warning for refining and chemical highly hazardous systems[D]. Beijing: China University of Geosciences, 2010. |



