1 引言
混沌运动作为复杂的非线性运动受到人们的广泛关注,早期研究的混沌系统有Lorenz系统、 Chen[1, 2]系统和Lü系统[3, 4, 5]等. 随着对混沌系统的深入研究,先后发现了一些新的混沌系统[6, 7, 8, 9]及一些具有恒李亚普诺夫指数谱混沌锁定的新混沌系统[10, 11, 12, 13]. 新系统的一些性质,如调幅特性、 倒相特性,可以省去工程应用中对混沌信号进行同相(反相)放大(缩小)时增加硬件的需求,也避免了许多由于增加硬件设备而增加的工程难度及成本. 发现和研究具有新性质的混沌系统具有工程意义和实用价值. 近年来,混沌系统在保密通信等领域获得新的应用,其通信系统的保密性取决于混沌系统的复杂性. 因此产生复杂的混沌吸引子以及构造具有多涡卷[14, 15, 16, 17]或多翅膀[18, 19]拓扑结构的吸引子成为研究的一个热点. 文[18, 19]分别研究多翅膀与网格多翅膀混沌系统,但是均未对其混沌系统特性进行分析.
本文提出了一个新的三维二次自治混沌系统,新系统具有以下性质: 双参数恒李亚普诺夫指数谱混沌锁定、 全局(局部)非线性调幅特性、 倒相特性等. 通过设计合理的非线性函数,即构造偶对称多分段平方函数族,可将该系统扩展成一个有多翅膀混沌吸引子的混沌系统. 电路仿真验证了系统的可实现性. 对扩展后的多翅膀混沌系统进行同步控制分析,说明了扩展后的混沌系统可实现同步控制. 这些性质使新系统具有工程应用价值.
2 新混沌系统模型考虑的新混沌系统模型如式(1)所示:
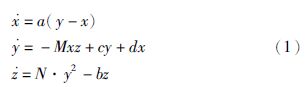
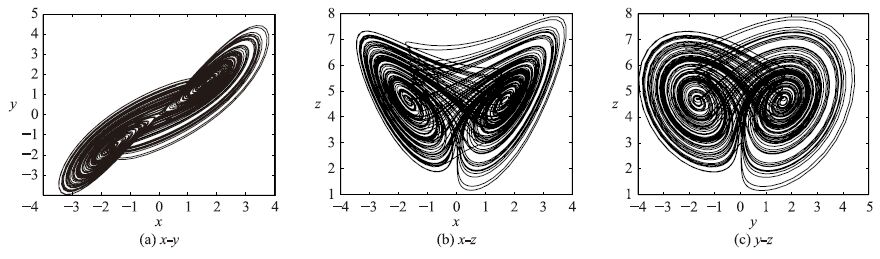
|
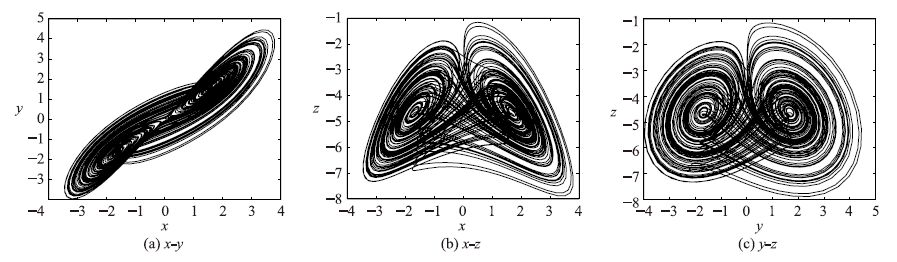
| 图 1 当a=25,b=3,c=15,d=8,M=5,N=5时奇怪吸引子在相平面上的投影 Fig. 1 Phase portraits of the new chaotic system when a=25,b=3,c=15,d=8,M=5,N=5 |
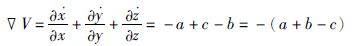
新系统(1)关于z轴对称,即通过坐标变换(x,y,z)→(-x,-y,z),系统的模型并未发生改变.
3.3 平衡点和稳定性令新系统(1)右边等于0,可得其平衡状态方程为
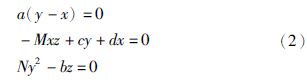
注意到如果b(c+d)MN>0(给定的参数满足该条件),则解方程组(2)有3个平衡点:
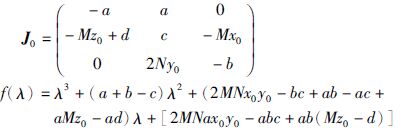
系统在平衡点处线性化,得雅可比矩阵J0和特征多项式f(λ),其中有:
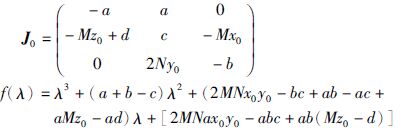
平衡点处对应的特征多项式可简化为f(λ)=λ3+(a+b-c)λ2+(2bd+bc+ab)λ+2ab(c+d)代入给定的参数值,平衡点S2,S3对应特征根为λ1=-15.99,λ2,3=1.49±14.6i,其属于指标2的鞍焦平衡点[21],系统具有混沌特性.
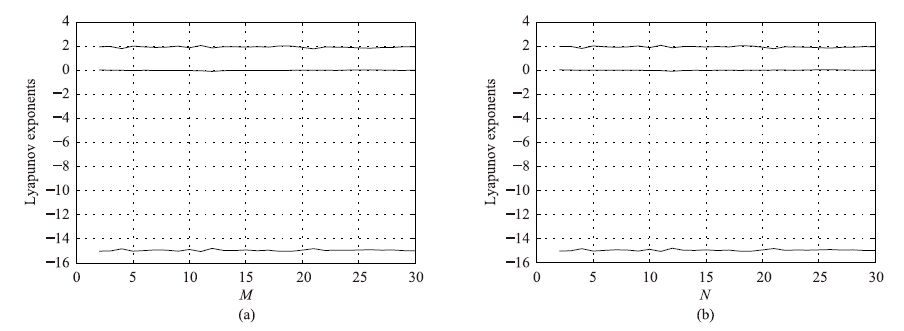
4 参数对系统性能的影响 4.1 双恒李亚普诺夫指数锁定当固定参数a=25,b=3,c=15,d=8,N=5,系统的李亚普诺夫指数谱随M变化如图 2(a)所示; 当固定参数a=25,b=3,c=15,d=8,M=5,系统的李亚普诺夫指数谱随N变化如图 2(b)所示. 由图可看出,系统的李亚普诺夫指数谱不随M和N的变化而改变. 同时观察化简后的特征多项式f(λ),可以发现,新系统在平衡点处雅可比矩阵对应的特征多项式与M和N无关,因此变量M和N不影响系统在平衡点处的动力学特征,系统的李亚普诺夫指数谱保持不变,实现恒李亚普诺夫指数谱的混沌锁定. 但实际计算由于受到计算精度的影响,李亚普诺夫指数会发生微小的波动,可以忽略不计.
|
| 图 2 固定其中5个参数,当其中一个参数变化时系统的李亚普诺夫指数谱 Fig. 2 Fix other five parameters,the Lyapunov exponent spectrums when one parameter varies |
调节参数M和N的取值,可以实现全局非线性调幅和局部非线性调幅特性. 其中在保持其他参数不变的情况下,M为全局非线性调幅参数,N为局部非线性调幅参数. 不难从系统的变换中验证参数M和N的调幅作用,如对系统进行非线性变换,令:
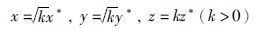
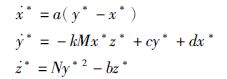
由此可看出变换后的输出信号x、 y和z与M的非线性关系,即M为全局非线性调幅参数. 同理设x=kx*,y=ky*,z=z*(k>0),可验证N为局部非线性调幅参数. 对其进行Matlab仿真验证: 固定a,b,c,d的取值,分别、 单独变化M和N,观察x,y,z随参数变化时幅值变化情况,仿真结果如图 3、 图 4所示. 输出信号x,y的幅值变化与M呈幂函数关系,其指数为-1/2; 输出信号z的幅值也与M呈幂函数关系,指数为-1. N为局部非线性调幅参数,输出信号x,y与N呈幂函数关系,指数为-1/2,而输出信号z与N的变化无关.
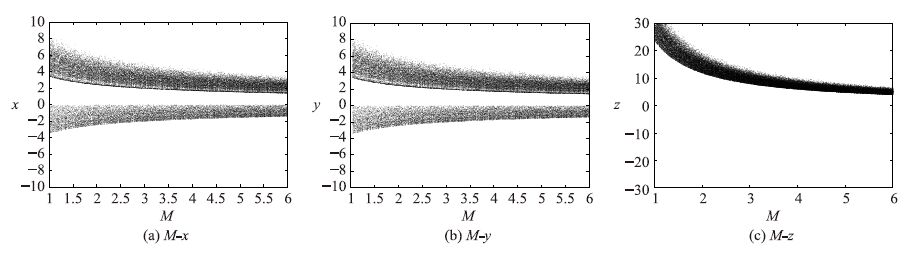
|
| 图 3 固定a=25,b=3,c=15,d=8,N=5,M变化时的分岔图 Fig. 3 Fix a=25,b=3,c=15,d=8,N=5,the bifurcation diagrams when M varies |
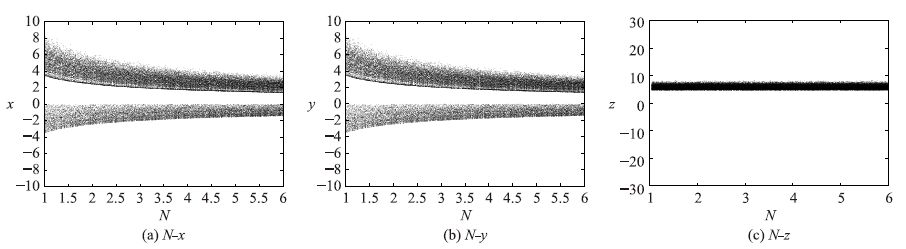
|
| 图 4 固定a=25,b=3,c=15,d=8,M=5,N变化时的分岔图 Fig. 4 Fix a=25,b=3,c=15,d=8,M=5,the bifurcation diagrams when M varies |
调幅参数M和N单独作用没有倒相作用,但是当同时变化M和N的符号时,调幅参数MN具有倒相作用. 对新系统进行变换: (x,y,z,a,b,c,d,M,N)→(x,y,-z,a,b,c,d,-M,-N)发现系统具有不变性,即新系统的输出信号z的符号将随着参数M和N的极性的改变而改变. 如图 5所示,图中新系统的吸引子正好沿z方向颠倒. 将MN定义为倒相参数. 调幅参数的倒相特性对该系统应用于混沌通信以及其他信息处理系统中具有重要的意义.
|
| 图 5 当a=25,b=3,c=15,d=8,M=-5,N=-5奇怪吸引子在相平面上的投影 Fig. 5 Phase portraits of the new chaotic system when a=25,b=3,c=15,d=8,M=-5,N=-5 |
新系统含有指标2的鞍焦平衡点,同时在变换(x,y,z)→(-x,-y,z)下具有不变性,因此可以通过构造一类新的偶对称多分段函数族fi(y)来实现系统的多翅膀扩展[21]. 在系统(1)的基础上,得多翅膀混沌系统的状态方程为
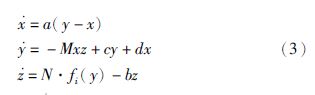
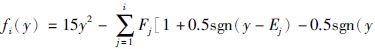 +Ej)],取数规则:
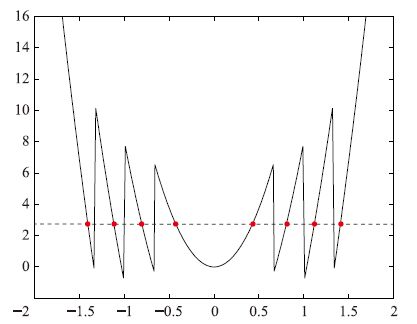
+Ej)],取数规则: 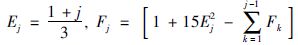 ,j≥2,F1=[1+15E12]=7,为了计算方便,[1+15Ej2]表示取整数部分,则: E1=0.667,E2=1,E3=1.33,E4=1.67,…,F2=9,F3=11,F4=15,…,图 6为多分段非线性函数族fi(y)的函数图像.
,j≥2,F1=[1+15E12]=7,为了计算方便,[1+15Ej2]表示取整数部分,则: E1=0.667,E2=1,E3=1.33,E4=1.67,…,F2=9,F3=11,F4=15,…,图 6为多分段非线性函数族fi(y)的函数图像.
|
| 图 6 多分段平方函数族fi(y)的函数图像(i=3) Fig. 6 Graphs of the multi-section square function fi(y)(i=3) |
令式(3)右边等于0,可得系统的平衡状态方程为
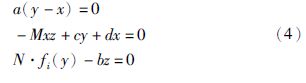
解方程组(4)可得系统平衡点的计算公式为
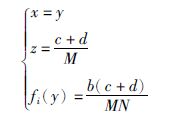
多翅膀系统的各个平衡点的坐标表示为
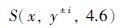
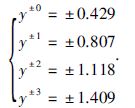
系统的平衡点所对应的特征值为
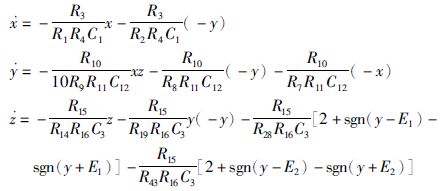
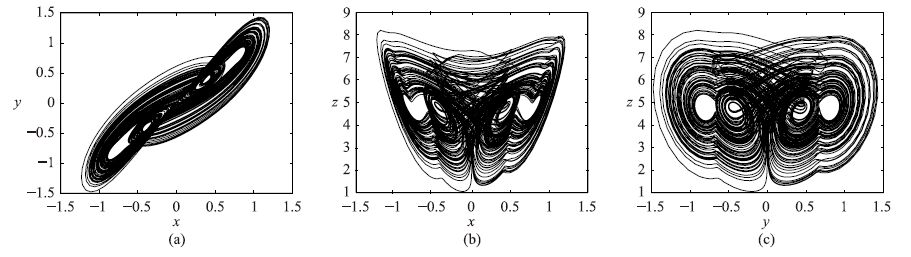
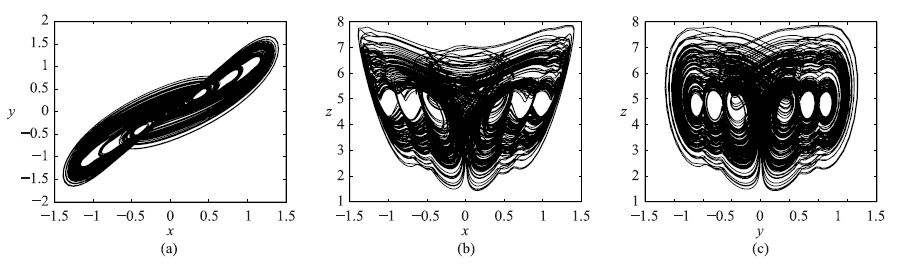
由此可看出,扩展后的系统的平衡点增加,且均为指标2的鞍焦平衡点,而系统的每一个指标2的鞍焦平衡点都可以产生一对翅膀. 因此当i=1、 i=2、 i=3时,系统分别被扩展成为4翅膀、 6翅膀和8翅膀吸引子. 仿真结果如图 7~图 9所示.
|
| 图 7 4翅膀混沌吸引子 Fig. 7 4-wing chaotic attractor |
|
| 图 8 6翅膀混沌吸引子 Fig. 8 6-wing chaotic attractor |

|
| 图 9 8翅膀混沌吸引子 Fig. 9 8-wing chaotic attractor |
扩展成多翅膀后的混沌系统,具有更复杂的动力学特性,不再具有原混沌系统的双恒李亚普诺夫指数谱、 调幅特性,以及倒相特性.
6 电路仿真验证为了进一步说明上述分析的正确性,下面对其进行电路仿真,以6翅膀为例. 应用电路仿真软件Multisim13.0搭建系统的模拟电路,运算放大器的型号均为LM348N,乘法器均为Multisim中的乘法器模块,电源供电电压均为±15 V. 对系统作时间尺度变换,将方程中的t变换成τ0t,其中τ0为时间尺度变换因子τ0=100,则:
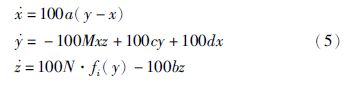
根据式(5)设计相应的电路模块并将输入、 输出对应项连接,可得系统的电路实现,如图 10所示. 文中以i=2为例说明. 根据图 10,可得该电路的状态方程为
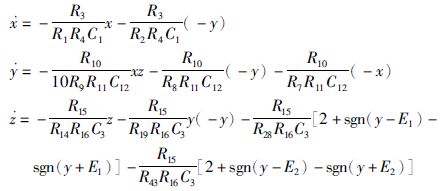
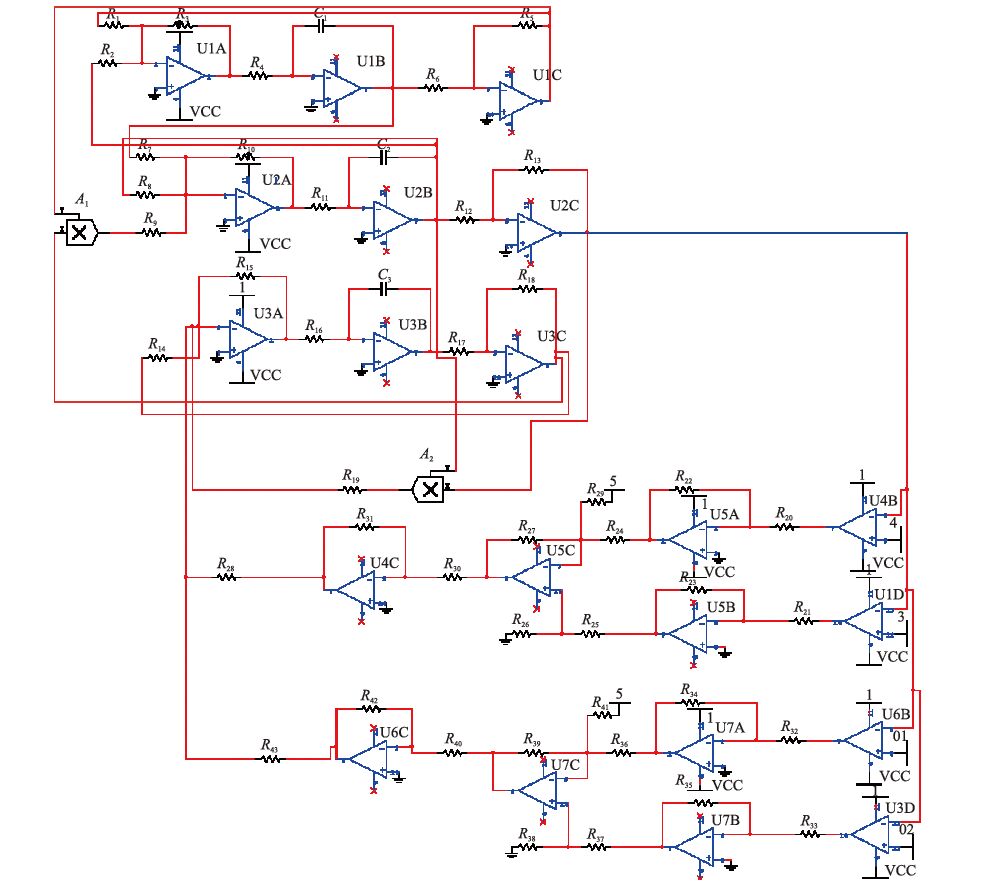
|
| 图 10 多翅膀混沌系统的电路实现(以i=2为例) Fig. 10 Circuit implementation of multi-wing chaotic system when i=2 |
与式(5)进行比较,对应系数相等则有: R1=R2=4 kΩ,R7=12.5 kΩ,R8=6.67 kΩ, R9=2 kΩ,R14=33.3 kΩ,R19=13.3 kΩ,R28=57.14 kΩ,R43=44.4 kΩ.系统的电路仿真结果如图 11所示,其为i=2时扩展成的6翅膀混沌吸引子在各个相平面上的投影.
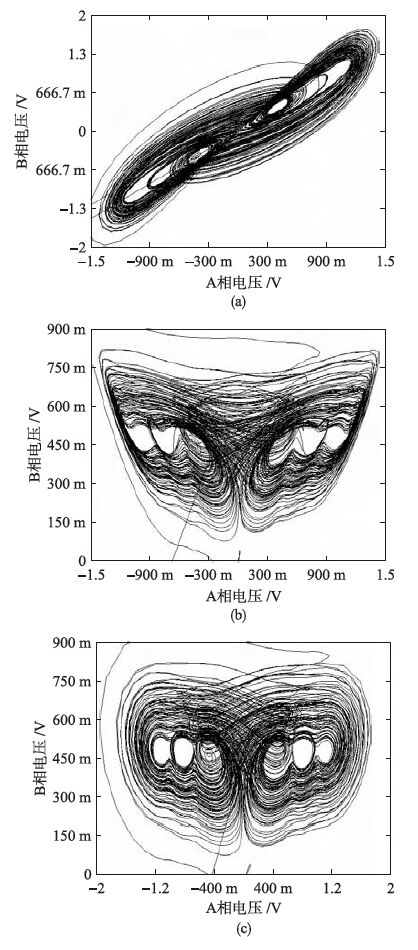
|
| 图 11 当i=2时通过电路实现的6翅膀混沌吸引子 Fig. 11 6-wing chaotic attractor by circuit implementation when i=2 |
可以对扩展后的多翅膀混沌系统进行同步控制,为了研究方便起见,文中以i=3为例.
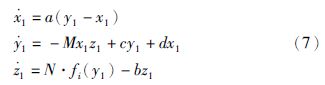
响应系统:
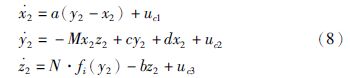
根据文[22]可知,对于系统结构相同的两个混沌系统,其误差系统可表示为
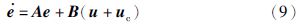
对应文中的多翅膀混沌系统,其中有:
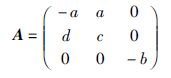
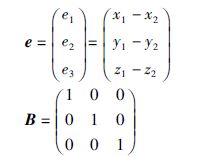
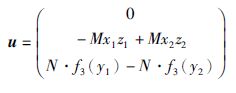
 为系统的同步控制器. 根据文[22]中的定理1可知,存在同步控制器uc=-KCe使得响应系统(8)与驱动系统(7)达到同步. 此时:
为系统的同步控制器. 根据文[22]中的定理1可知,存在同步控制器uc=-KCe使得响应系统(8)与驱动系统(7)达到同步. 此时:
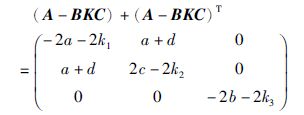
其各阶顺序主子行列式分别为
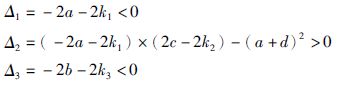
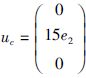 0,此时,响应系统(8)和驱动系统(7)能达到同步.
0,此时,响应系统(8)和驱动系统(7)能达到同步.
此时的响应系统和驱动系统分别可表示为
驱动系统:
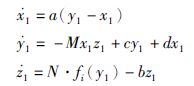
响应系统:
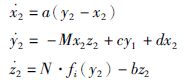
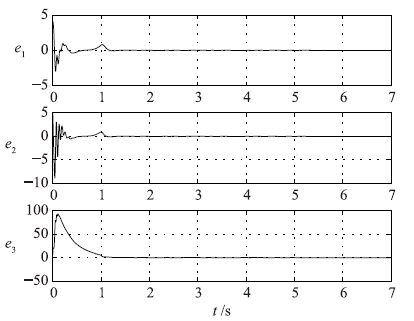
对驱动系统和响应系统的同步进行Matlab仿真验证,两系统的初值可以任意选取,现选取驱动系统的初值为: (x10,y10,z10)=(1,1,1),响应系统的初值为: (x20,y20,z20)=(5,6,7). 两系统的误差系统的数值仿真结果如图 12所示. 由图可以看出,1.3 s左右两系统的误差几乎为0,大致达到同步,经过5.5 s即可达到完全同步.
|
| 图 12 响应系统与驱动系统的误差曲线图 Fig. 12 Error curve of the response system and the drive system |
本文给出了一个新的三维二次自治混沌系统,理论分析和仿真验证了新混沌系统具有如下性质: 双参数恒李亚普诺夫指数谱混沌锁定、 全局(局部)非线性调幅参数、 倒相参数等. 根据新系统的平衡点和吸引子的拓扑结构,本文通过设计合理的非线性函数将其扩展成为具有多翅膀混沌吸引子的混沌系统,并通过电路仿真进行验证. 扩展后的多翅膀混沌系统更复杂,不再保持原有的一些特性,但可以实现同步控制. 本文通过选取合适的驱动信号,实现响应系统与驱动系统混沌同步,方法简单且同步速度较快. 本文提出的混沌系统与扩展成多翅膀后的混沌系统可应用于保密通信及其它混沌控制,相关问题有待于进一步的研究.
| [1] | Chen G R, Ueta T. Yet another chaotic attractor[J]. International Journal of Bifurcation and Chaos, 1999, 9(7): 1465-1466. |
| [2] | Ueta T, Chen G R. Bifurcation analysis of Chen's equation[J]. International Journal of Bifurcation and Chaos, 2000, 10(8): 1917-1931. |
| [3] | Lü J H, Chen G R. A new chaotic attractor coined[J]. International Journal of Bifurcation and chaos, 2002, 12(3): 659-661. |
| [4] | Lü J H, Chen G R, Cheng D Z, et al. Bridge the gap between the Lorenz system and the Chen system[J]. International Journal of Bifurcation and Chaos, 2002, 12(12): 2917-2926. |
| [5] | Lü J H, Chen G R, Zhang S C. Dynamical analysis of a new chaotic attractor[J]. International Journal of Bifurcation and chaos, 2002, 12(5): 1001-1015. |
| [6] | 唐良瑞, 李静, 樊冰. 一个新四维自治超混沌系统及其电路实现[J]. 物理学报, 2009, 58(3): 1446-1455. Tang L R, Li J, Fan B. A new four-dimensional hyper-chaotic system and its circuit simulation[J]. Acta Physica Sinica, 2009, 58(3): 1446-1455. |
| [7] | 蔡国梁, 谭振梅, 周维怀, 等. 一个新的混沌系统的动力学分析及混沌控制[J]. 物理学报, 2007, 56(11): 6230-6237. Cai G L, Tan Z M, Zhou W H, et al. Dynamical analysis of a new chaotic system and its chaotic control[J]. Acta Physica Sinica, 2007, 56(11): 6230-6237. |
| [8] | 王杰智, 陈增强, 袁著祉. 一个新的混沌系统及其性质研究[J]. 物理学报, 2006, 55(8): 3956-3963. Wang J Z, Chen Z Q, Yuan Z Z. A new chaotic system and analysis of its properties[J]. Acta Physica Sinica, 2006, 55(8): 3956-3963. |
| [9] | 王发强, 刘崇新. Liu 混沌系统的混沌分析及电路实验的研究[J]. 物理学报, 2006, 55(10): 5061-5069. Wang F Q, Liu C X. Studies on Liu chaotic system and its experimental confirmation[J]. Acta Physica Sinica, 2006, 55(10): 5061-5069. |
| [10] | 李春彪, 陈谡, 朱焕强. 一个改进恒Lyapunov指数谱混沌系统的电路实现与同步控制[J]. 物理学报, 2009, 58(4): 2255-2265. Li C B, Chen S, Zhu H Q. Circuit implementation and synchronization of an improved system with invariable Lyapunov exponent spectrum[J]. Acta Physica Sinica, 2009, 58(4): 2255-2265. |
| [11] | 李春彪, 徐克生, 胡文. Sprott系统的恒Lyapunov指数谱混沌锁定及其反同步[J]. 物理学报, 2011, 60(12): 120504-120515. Li C B, Xu K S, Hu W. Sprott system locked on chaos with constant Lyapunov exponent spectrum and its anti-synchronization[J]. Acta Physica Sinica, 2011, 60(12): 120504-120515. |
| [12] | 李春彪, 王翰康, 陈谡. 一个新的恒Lyapunov指数谱混沌吸引子与电路实现[J]. 物理学报, 2010, 59(2): 783-791. Li C B, Wang H K, Chen S. A novel chaotic attractor with constant Lyapunov exponent spectrum and its circuit implementation[J]. Acta Physica Sinica, 2010, 59(2): 783-791. |
| [13] | 周小勇. 一种具有恒Lyapunov指数谱的混沌系统及其电路仿真[J]. 物理学报, 2011, 60(10): 54-65. Zhou X Y. A chaotic system with invariable Lyapunov exponent and its circuit simulation[J]. Acta Physica Sinica, 2011, 60(10): 54-65. |
| [14] | 罗小华, 李华青, 代祥光. 一类多涡卷混沌吸引子及电路设计[J]. 物理学报, 2008, 57(12): 7511-7516. Luo X H, Li H Q, Dai X G. A family of multi-scroll chaotic attractors and its circuit design[J]. Acta Physica Sinica, 2008, 57(12): 7511-7516. |
| [15] | Tang W K S, Zhong G Q, Chen G, et al. Generation of n-scroll attractors via sine function[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2001, 48(11): 1369-1372. |
| [16] | Zhang C X, Yu S M. Design and implementation of a novel multi-scroll chaotic system[J]. Chinese Physics B, 2009, 18(1): 119-130. |
| [17] | Shen C W, Yu S M, Lü J H, et al. A systematic methodology for constructing hyperchaotic systems with multiple positive Lyapunov exponents and circuit implementation[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2014, 61(3): 854-864. |
| [18] | 王建华, 卢鑫. 一个多翅膀混沌系统的设计[J]. 西南大学学报: 自然科学版, 2012, 34(5): 57-63. Wang J H, Lu X. The Design of a Multi-wing Chaotic System[J]. Journal of Southwest University, 2012, 34(5): 57-63. |
| [19] | 周欣, 王春华, 郭小蓉. 一个新的网格多翅膀混沌系统及其电路实现[J]. 物理学报, 2012, 61(20): 200506-200516. Zhou X, Wang C H, Guo X R. A new grid multi-wing chaotic system and its circuit implementation[J]. Acta Physica Sinica, 2012, 61(20): 200506-200516. |
| [20] | 杨晓松, 李清都. 混沌系统与混沌电路[M]. 北京: 科学出版社, 2007: 5-11.Yang X S, Li Q D. Chaotic Systems and Chaotic Circuits[M]. Beijing: Science Press, 2007: 5-11. |
| [21] | 禹思敏. 混沌系统与混沌电路: 原理, 设计及其在通信中的应用[M]. 西安电子科技大学出版社, 2011. Yu S M. Chaotic systems and chaotic circuits: Principle, design and its application in communications[M]. Xi'an Electronic Science & Technology University Press, 2011. |
| [22] | 牛弘, 张国山. 一类具有可变系数的混沌系统的同步[J]. 物理学报, 2013, 62(13): 130502-130513. Niu H, Zhang G S. Synchronization of chaotic systems with variable coefficients[J]. Acta Physica Sinica, 2013, 62(13): 130502-130513. |



