1 引言
先进机场场面引导与控制系统[1](advanced surface movement guidance and control system,A-SMGCS)是国际民航组织提出的当前最先进的飞行区场面管理概念,其自动路由规划功能可辅助管制员协调航空器安全和高效滑行,在此方面欧美已展开较多研究[2, 3, 4, 5, 6, 7]. Marin[8, 9]将航空器滑行路由规划问题抽象为基于时空网络的多商品网络流优化问题,并采用分支定界(branch and bound)方法和固定松弛(fix and relax)方法求解. Garcia[10, 11]将路由规划问题转化为网络流量管理问题,采用最少费用最大流算法规划航空器滑行路由,并进一步将遗传算法(genetic algorithm,GA)与改进的最少费用最大流算法结合. Pesic[12]基于航空器滑行预选路径,采用GA规划航空器场面滑行路径. Gotteland[13]采用GA和A*算法规划航空器场面滑行路由. 由于受制于场面运行建模手段及算法对场面管制规则集成不足,以往研究难以支持A-SMGCS对场面运行实施精细化控制,因此,规划结果实用性有待提高. 而基于冲突避免的动态滑行路由规划[14],其假定航班滑行过程可改变滑行路径,此做法会增加管制员和飞行员的工作负荷. 汤新民[15]提出A-SMGCS三阶段路由规划策略:
(1)初始路径规划,即为进离港航班确定最优和s-1个次优滑行路径(s取值可通过管制自动化系统设定);
(2) 滑行路由指派,即在新航班加入前,基于其对应的初始滑行路径集和当前场面态势,为场面所有航班(包括新航班)指派合理的滑行路由;
(3) 路由实时更新,即为在航班滑行过程中实时调整路由以避免冲突,以应对不确定事件干扰. 以往针对初始路径规划已开展过研究[16],本文重点研究第(2)阶段的问题,即滑行路由指派.
2 问题描述如图 1所示,将飞行区场面交通系统划分成多个典型场面运行单元(包括交叉口单元和直线段单元). 假设存在航班a1和a2. 其中a1在其滑行路径上依次通过单元p1、 p3、 p5、 p6和p8,单向停止排灯b1点亮时可阻挡其由p1滑入p3,b5点亮时可阻挡其离开p8滑入其它单元,而a1在单元p3、 p5、 p6和p8组成的路段上可不受停止排灯阻挡而连续滑行(相应路段称为连续滑行路段); a2在其滑行路径上依次通过单元p2、 p3、 p5、 p6和p8,其连续滑行路段包括单元p3、 p5、 p6和p8. 另外,若有即将加入场面滑行的新航班a3(设采用文[16]所给方法已为其确定多条初始预选路径),此时若为航班a3选择其中一条预选路径滑行并依次通过单元p7、 p6、 p5、 p3和p4. 在此情形下,由于航班a1、 a2和a3可能会同时占用某些相同运行单元(p3、 p5或p6),因而需要合理规划航班占用各单元的时间,以避免在滑行路由指派阶段出现滑行冲突. 鉴于场面交通系统复杂,且实际运行中航班数量较多,如果不借助于精确的数学模型和求解算法,管制员难以在有限时间内兼顾多方利益并完成路由指派. 因此,如何建模和求解这一问题,是本文的主要工作.
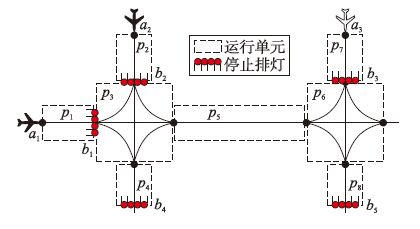
|
| 图 1 场面交通系统运行单元划分 Fig. 1 Operation unit division for surface taxiway system |
定义1 航班占用场面单元多参数时间窗为wap={p,[ita,ota],ra}. 其中,ita为航班a进入单元p(交叉口或直线段)的时刻; ota为a离开单元p的时刻; ra为a的连续滑行路段(由沿滑行路径和能阻止航班a滑行的连续两个停止排灯之间的若干单元构成),且该路段包含单元p.
定义2 场面航班滑行路由为W={wai}(i=1,2,…,q),其中,q为场面滑行航班的数量; wai={waip1,waip2,…,waipn},其中waipn为航班ai占用场面运行单元的时间窗,p2,p2,…,pn为航班ai滑行路径上包含的运行单元.
依据加入场面滑行时刻的先后,场面运行过程中,所有航班场面滑行请求设为序列∂=(α1,α2,α3,…). Πi={ri1,ri2,…,rin}为航班i的初始预选滑行路径集合. 假设场面已开始滑行航班的滑行路径不变,但其占用路径上各单元的时间窗可调整. 航空器滑行路由指派可描述为: 在新航班加入场面时刻,依据正在滑行航班的路由W={waj}(j=1,2,…,q-1)和新航班初始预选路径集Πi,为上述所有航班指派滑行路由,使场面运行满足:
(1) 若各航班严格遵循所指派路由占用场面单元,无场面滑行冲突;
(2) 在路由指派阶段,当前所有航班(包括已开始滑行航班和新航班)场面滑行成本最小. 满足要求(1)的路由称为可行路由,满足(1)~(2)的路由称为合理路由.
3 场面运行过程建模 3.1 模型基本定义与构造算法定义3 场面时间窗约束Petri网模型为TWCPN={P,T,Q,M0,Ψ},其中,库所p∈P表示场面单元(如滑行道交叉口或直线段); 变迁集T=T1∪T2,T1表示可受停止排灯阻止的航空器穿越场面单元边界活动,用黑盒变迁“”描述,T2表示不受停止排灯阻止的航空器穿越场面单元边界活动,用单线变迁“”描述; Q: (P×T)∪(T×P)→Z+为库所和变迁之间弧的权值函数; M0为模型初始标识,可描述场面单元的航班占用状态; Ψ: P→W为航班占用场面单元多参数时间窗映射,可描述航班对场面单元的占用过程.
算法1 场面TWCPN模型构造算法.
输入: 场面正在滑行航班的路径集合R={ri}(i=1,2,…,q),新航班滑行路径rq∈Πq;
输出: 场面运行TWCPN模型.
Step 1: 对航班i而言,设其后续滑行路径表示为变迁序列ri=(ti1,ti2,…,tih-1,tih). 将该航班在运行单元Omn上的滑行过程用变迁tim、 tin(1≤m≤h-1,2≤n≤h)和具有相应时间窗的库所pmn来表示(其中tim,tin分别为库所pmn的输入和输出变迁),记为子模型Nmn;
Step 2:对所有模型Nmn依据ri=(ti1,ti2,…,tih-1,tih)中变迁出现的先后顺序采用同步合成技术[17]进行连接,并令库所p∈i*t1标识满足M(p)=1,最终得到航班沿路径ri滑行的场面运行子模型Ni;
Step 3:对R中所有滑行路径,均采用Step 1和Step 2构建对应的场面运行子模型Ni(i=1,2,…,q);
Step 4: 将子模型Ni(i=1,2,…,q)中表示同一场面单元的库所叠加,得到TWCPN模型.
例1 以图 1所示场面运行过程为例,将正在滑行航班a1、 a2的后续路径组成集合R={r1,r2},其中a1的路径为r1=(t11,t12,t13,t14,…),a2的路径为r2=(t21,t22,t23,t24,…),且变迁t11和t21描述航空器活动可受停止排灯阻止. 利用算法1可得对应TWCPN模型如图 2(a)所示. 其中,变迁t12和t22、 t13和t23分别表示a1、 a2滑行过程中穿越相同的单元边界活动. 当新航班a3选择某一初始路径r3∈Πi加入场面滑行时,若其某一路段上依次经过单元p7、 p6、 p5、 p3和p4对应路径r3=(t31,t32,t33,t34,…),且t31对应的航空器活动可受停止排灯阻止. 此时,进一步利用算法1得到对应TWCPN模型如图 2(b)所示.
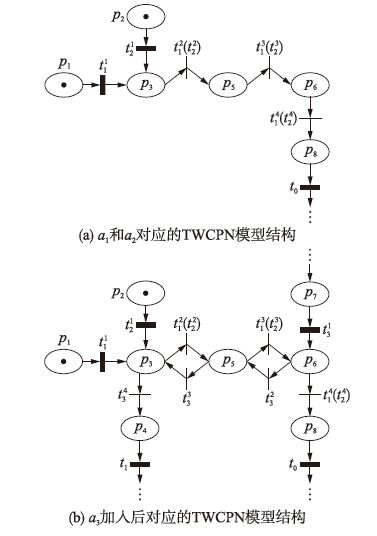
|
| 图 2 图 1所示交通系统中场面TWCPN模型 Fig. 2 TWCPN model for taxiway system in Fig. 1 |
A-SMGCS对航班采取分段放行策略,每次均将航班放行至滑行路径上对其有阻挡作用的停止排灯之前为止.
定义4 TWCPN模型中连续滑行路段为rk(n,m)=(tn,tn+1,…,tm-1,tm),其中rk为某一航班的滑行路径,变迁序列(tn,tn+1,…,tm-1,tm)中tn和tm为黑盒变迁,其它变迁均为单线变迁.
记TWCPN模型中rk(n,m)的单元库所集合Pk(n,m)={pp∈tj*∩*tj+1,tj∈rk(n,m)}.
定义5 关联路段,若不同航班的连续滑行路段rk(n,m)和rh(e,z)所含库所集之间满足关系Pk(n,m)∩Ph(e,z)≠Φ,则称rk(n,m)和rh(e,z)互为关联路段.
TWCPN模型中变迁t∈T1使能条件为:
(1) 变迁t的输入库所pi满足M(pi)=1;
(2) 航班在库所对应单元的滑行计时v(t)=xi+dτi,其中xi为库所pi被标识时刻,dτi为航班在对应单元滑行时长;
(3) 航班下一个连续滑行路段上,其库所集满足∑jM(pj)=0;
(4) 航班下一个连续滑行路段的关联路段未被其他航班占用.
上述条件(1)、 (2)表明航班对某一单元的占用符合实际滑行过程; 条件(3)、 (4)保证了规划阶段航班滑行冲突避免,基于此可将航空器视为质点. 当满足条件(1)~(3)时,称变迁t∈T1为弱使能; 满足条件(1)~(4)时,称变迁t∈T1为强使能. 航班在连续滑行路段中滑行不受停止排灯阻挡,因而对TWCPN模型中变迁t∈T2而言,当满足条件(1)、 (2)时,称其为强使能.
在标识M下,若变迁t∈T1∪T2满足强使能条件,则立即激发并产生新标识M′,M′(pi)=M(pi)-Q(pi,t)(∀pi∈(*t-t*)),M′(pi)=M(pi)+Q(pi,t)(∀pi∈(t*-*t)). 其中,*t和t*分别为变迁的输入和输出库所集合.
若多个黑盒变迁t∈T1同时处于强使能情形,其优先激发选择规则为:
(1) 进港航班托肯使能的黑盒变迁应优先激发;
(2) 离港航班中专机或要客航班托肯使能的黑盒变迁应优先激发.
4 可行路由求解航班对每个场面运行单元或某一连续滑行路段的占用均会持续一段时间(称之为占用不变状态). 定义TWCPN模型运行的不变状态如下.
定义6 场面单元占用不变状态为CIki=(pi,xi,[τ1,τ2],rk(n,m)),其中,k为航班号,pi为被标识的场面运行单元库所; xi为库所被标识时刻; [τ1,τ2]为航班占用库所pi的时间段; rk(n,m)为航班在该状态下所处连续滑行路段; 在时间段[xi,xi+(τ2-τ1)]内,库所pi的标识保持不变.
定义7 连续滑行路段占用不变状态为LIk=(rk(n,m),[η1,η2],{CIki}). 其中,rk(n,m)为航班当前所处连续滑行路段,[η1,η2]为航班占用该路段的时间段,{CIki}为航班在该路段上各单元占用不变状态集合; 在时间段[η1,η2]内,该路段上的场面运行单元库所p∈Pk(n,m)仅被同一航空器对应托肯标识.
算法2 基于不变状态的TWCPN模型行为演变算法
输入: 当前标识M,目标标识M′,路径rk;
输出:集合LIS={LI1,LI2,…,LIq}.
Step 1: 初始化不变状态集合LIS=Φ;
Step 2:各航班滑行路径rk依据定义4得到rk的连续滑行路段集合{rk(n,m)},并确定各个连续滑行路段对应单元库所集合Pk(n,m);
Step 3: 在当前标识M下,若存在Pi∈Pk(n,m)满足M(pi)=1,则对变迁t∈Pi依据变迁使能和激发规则激发,由定义6确定Pi对应的CIki,由定义7确定所在路段LIk,并将LIk加入LIS;
Step 4: 设Step 3中模型标识为M1. 确定在M1下的强使能黑盒变迁t∈T1,并组成集合ET1;
Step 5: 对ET1中黑盒变迁按照优先激发规则,确定应优先激发的变迁集合PET1; 随机选择变迁t∈ET1\PET1组成次优先激发变迁集合PET2;
Step 6: 判断模型是否已达目标标识M′,若是,则退出算法; 否则,继续Step 3~Step 5.
∀LIi∈LIS表示航班对连续滑行路段的占用过程,且根据变迁使能规则可知,不变状态所描述的航班滑行过程无冲突存在. 由算法2可得LIS对应于场面所有航班的一个可行滑行路由.
5 合理路由指派算法利用单亲遗传算法(partheno-genetic algorithm,PGA)[18, 19]基于算法2所得可行滑行路由实现合理路由求解. 具体设计如下:
(1) 产生初始种群: 对算法2生成的不变状态集合LIS={LI1,LI2,…,LIq}按如下方式编码: 将LIS所含元素分成如图 3所示的k段(对应于模型演变至目标标识过程中所经历的k次变迁激发),满足同一段内各不变状态对应的航班开始占用路段时刻相同,但同一段内所含不变状态的排列没有实际意义. 将上述方式产生的染色体加入初始种群.
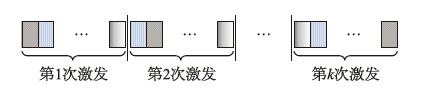
|
| 图 3 PGA编码方式 Fig. 3 PGA coding method |
(2) 设计换位变异混合算子: 任一航班对应于某一连续滑行路段的LIk在染色体中只出现一次,且航班在连续滑行路段上占用各单元存在先后约束,如采用标准遗传算法的交叉操作,有可能产生不满足上述约束的无效染色体. 因此,设计一种换位变异混合算子进行遗传操作.
具体方法为:
① 随机选择染色体上属于连续两个激发批次的两个不变状态,如图 4中不变状态a,b(所在批次的开始激发时刻为ti,ti+1);
② 对属于第i+1个激发批次的不变状态b,若激发使其出现的变迁在前一激发批次开始时属于强使能变迁,则将不变状态b放入第i个激发批次并记为b′,同时将其开始时刻改为ti,而将该航空器上一不变状态的结束时刻也改为ti;
③ 对属于第i个激发批次的不变状态a,直接将其放于第i+1个激发批次并记为a′,同时将其开始时刻改为ti+1,而该航空器的上一不变状态的结束时刻也改为ti+1;
④ 从ti时刻开始,重新确定包含不变状态b′的第i个新的激发批次,并以此为模型演化起点,利用算法2计算后续不变状态集合(第i+1个激发批次中应包含不变状态a′),按照所给编码方式生成新染色体. 具体操作如图 4所示. 如此设计的遗传操作算子既可保证新个体具有可行解的基本特征,同时又可提高对可行解空间的搜索能力.
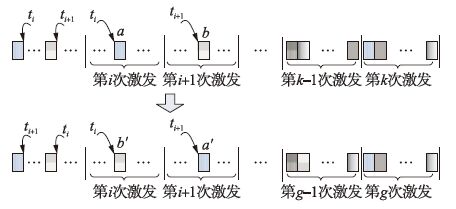
|
| 图 4 PGA换位变异混合算子操作过程 Fig. 4 Mixed switch and mutation operation of PGA |
(3) 适应度函数: 将染色体中属于同一航班的不变状态按照起始时刻的先后排列,生成如图 5所示的不变状态排列(设此时有包括新航班在内的q个航班参与场面滑行).
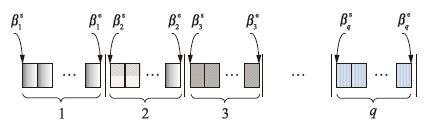
|
| 图 5 不同航班对应的不变状态排列 Fig. 5 Invariable state sequence of different flights |
在同一航班的不变状态排列中,第一个不变状态的起始时刻记为βis,最后一个不变状态的终止时刻记为βie. 设进离港航班集合分别为A和D. 染色体适应度函数设计如下:
J(q)=J(A)+J(D)
进港航班滑行成本为
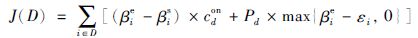
离港航班滑行成本为
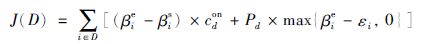
(4) 选择复制: 采用轮盘赌选择机制,群体中染色体复制比例根据适应值所占比例而定,并同时加入最优保持策略以保证算法全局收敛性.
(5) 停止准则: 达到最大迭代次数立即终止.
综上,航班滑行合理路由指派算法如下:
Step 1: 确定当前应指派路由的新航班,任选其初始预选路径r∈Πi={ri1,ri2,…,rin};
Step 2: 利用算法1构建新航班加入场面滑行后的场面TWCPN模型;
Step 3: 利用算法2确定所建TWCPN模型中各航班场面滑行可行路由;
Step 4: 利用可行滑行路由结果,采用本文所给PGA算法确定各航班场面滑行合理路由;
Step 5: 为每一新航班选择初始预选路径,然后均进行Step 2~Step 4,完成后转Step 6;
Step 6: 新航班按不同初始预选路径滑行时,场面航班进行多个合理路由方案对比,选择成本最小的路由指派给场面航班执行.
6 仿真实验 6.1 实验设计基于Anylogic软件构建仿真平台,并以某机场为例进行仿真实验. 该机场目前路由指派方式是为机坪内某些相邻机位的航班指派固定滑行路径,但不指派航班占用各单元的时间段(图 6为该机场01跑道运行时,进出各机位航班所采取的固定滑行路径). 将上述指派方式与本文路由指派方法进行对比分析. 两种方式下,均依据停止排灯来划分场面连续滑行路段,并采用一个工作日内停靠T3C\D\E东侧机位、 且使用01跑道的航班数据.
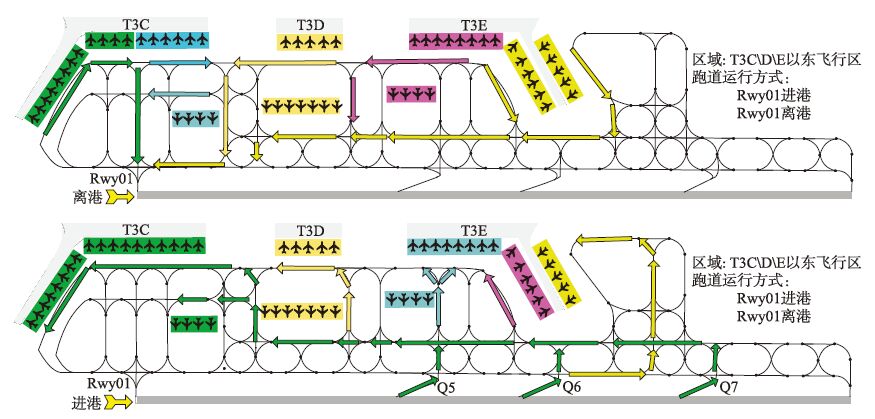
|
| 图 6 固定滑行路径方式下某机场01号跑道的进离港航班滑行路径 Fig. 6 The taxiing routes for arrival and departure flight of runway 01 under the constant taxi route assignment method |
设航空器在机坪滑行速度为5 m/s,在滑行道直线段滑行速度为8 m/s,在弯道滑行速度为5 m/s,且加速度为1 m/s2,减速度为2 m/s2(取负值). 航班滑行成本依据航班滑行油耗计算[20]. 设航班初始路径数量s=3. 离港航班尽可能按预计时间推至出等待位,然后指派从该位置至跑道头等待区的滑行路由; 所有进港航班均指派从脱离口至停靠机位的滑行路由. PGA种群规模为20,换位变异概率pc为0.5,进化代数为40.
6.2 实验结果分析 6.2 .1 滑行路由指派算法性能滑行路由指派算法包含TWCPN模型构造算法、 可行路由算法和合理路由求解算法. 由于场面停止排灯布局较均匀,因而航班连续滑行路段通常所含单元不多,TWCPN模型构造算法和可行路由求解算法仅涉及低维矩阵运算,复杂度较低,故路由指派算法性能主要受合理路由求解算法影响. 以该机场高峰时段中某一小时内01跑道航班滑行需求为基准(32架次,其中进港14架次、 离港18架次),并分别按20%(取6架次,进港3架次、 离港3架次)、 30%(取10架次,进港5架次、 离港5架次)增加航班架次,然后对不同情形展开多次实验. 统计多次实验每代遗传进化的滑行平均成本,其收敛曲线如图 7所示.
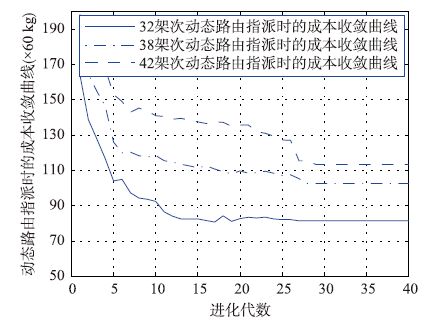
|
| 图 7 不同架次航班动态路由指派时成本收敛曲线 Fig. 7 Cost convergence curves for dynamic rout assignment method under different flight volumes |
可见,随着航班量的增加,算法收敛速度变慢,但均能在较短时间内获得合理的滑行路由. 采用所给编码和换位变异操作时,实际上仅是调整航班占用各单元的时间窗,由于单元数量有限且遗传操作避免了不可行解出现,因此,算法收敛性良好.
6.2.2 各时段内场面上航班的平均滑行时间利用所采集的航班数据,对图 6指派固定滑行路径方式和本文所给动态滑行路由指派方式进行仿真对比,统计各时段内(半小时划分为一个时段)场面上进离港航班平均滑行时间,如图 8和图 9所示. 可见,在采用本文动态滑行路径方式时,各时段内进离港航班的平均滑行时间较采用固定滑行路径方式时均有较大降低. 这表明,采用动态路由指派方式可缩短场面资源占用时间,更为高效地利用场面资源.
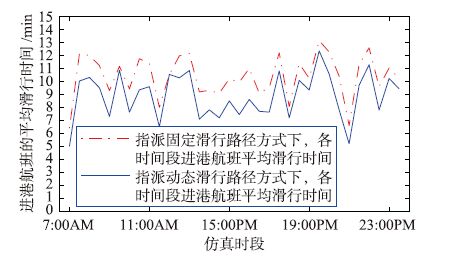
|
| 图 8 两种路径指派方式下进港航班平均滑行时间 Fig. 8 Mean taxiing time for arrival flight under two kinds of route assignment methods |
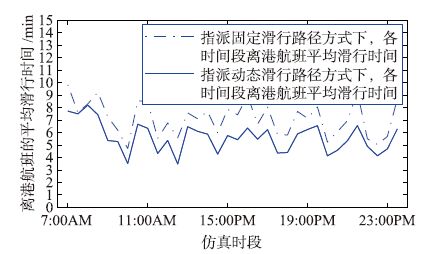
|
| 图 9 两种路径指派方式下离港航班平均滑行时间 Fig. 9 Mean taxiing time for departure flight under two kinds of route assignment methods |
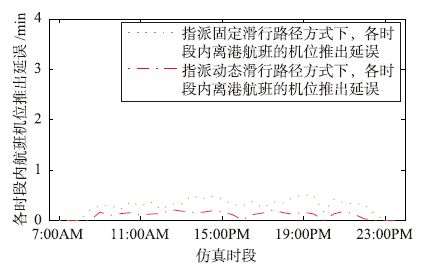
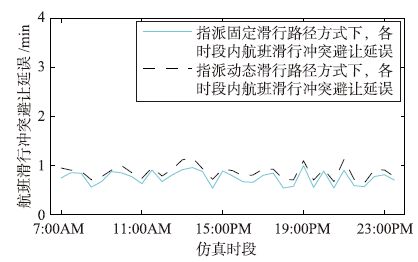
航班场面滑行延误包括机位推出延误、 中途滑行延误和跑道头等待延误. 两种方式下,各时段内的延误分别如图 10~图 12所示. 由图 10可知,两种方式下各时段内离港航班的跑道头等待延误均较为显著,这与仿真过程中采取尽可能满足航班推出请求策略有关. 由图 11可知,与固定滑行路径相比,采用本文动态滑行路径方式时,机位推出延误较小,这是由于每个离港航班有多条预选路径供选择,因而减少了推出等待延误. 但图 12表明,采用指派固定滑行路径方式时,滑行过程中冲突避让引起的延误较少,这是由于固定滑行路径较少出现对头滑行冲突且仅有少量交叉口冲突,因而用于避免冲突的等待时间较少.
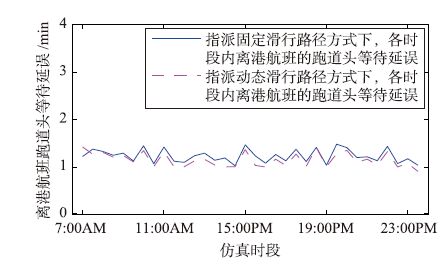
|
| 图 10 两种路径指派方式下离港航班跑道头等待延误 Fig. 10 Runway delay for departure flight under two kinds of route assignment methods |
|
| 图 11 两种路径指派方式下离港航班机位推出延误 Fig. 11 Gate delay for departure flight under two kinds of route assignment methods |
|
| 图 12 两种路径指派方式下航班滑行冲突避让延误 Fig. 12 Flight taxiing conflict avoidance delay under two kinds of route assignment methods |
本文提出一种航空器滑行路由指派方法,具有以下特点:
(1) 定义航班占用场面单元多参数时间窗,并建立场面运行TWCPN模型及描述航班对场面的占用过程;
(2) 给出基于不变状态的TWCPN模型行为演变算法,并通过该算法实现可行路由求解; 然后改进单亲遗传算法获得合理滑行路由,并最终实现航空器滑行路由指派;
(3) 采用Anylogic软件构建仿真实验平台,实现所给路由指派算法,并通过基于实际运行数据的仿真对比实验验证所给方法的有效性. 进一步研究应考虑场面运行不确定性,从而实现航空器场面滑行轨迹的预测和路由的实时更新.
| [1] | Delise R. Advanced surface movement guidance and control systems (A-SMGCS) manual[S]. Canada: International Civil Aviation Organization (ICAO), Doc. 9830-AN/452, 2004. |
| [2] | Carotenuto S. State of the art in A-SMGCS[R]. Germany: European Commission, 2005. |
| [3] | Atkin J, Burke E, Ravizza S. The airport ground movement problem: Past and current research and future directions[C]//4th International Conference on Research in Air Transportation. Piscataway, NJ, USA: IEEE, 2010: 131-138. |
| [4] | Clare G L, Richards A, Sharma S. Optimization of taxiway routing and runway scheduling[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1000-1013. |
| [5] | Montoya J, Wood Z, Rathinam S, et al. A mixed integer linear program for solving a multiple route taxi scheduling problem[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference. Keystone, CO, USA: AIAA, 2010: 1-18. |
| [6] | Clare G, Richards A, Sharma S. Receding horizon, iterative optimization of taxiway routing and runway scheduling[C]//Proceedings of the AIAA Modeling and Simulation Technologies Conference. Keystone, CO, USA: AIAA, 2009: 1-14. |
| [7] | Lee H, Balakrishnan H. Optimization of airport taxiway operations at detroit metropolitan airport (DMA)[C]//13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference. Keystone, CO, USA: AIAA, 2010: 1-16. |
| [8] | Marin A G. Airport management: Taxi planning[J]. Annals of Operations Research, 2006, 143(1): 191-202. |
| [9] | Marin A G, Salmeron J. Taxi planner optimization: A management tool[J]. Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering, 2008, 222(G7): 1055-1066. |
| [10] | Garcia J, Berlanga A, Molina J M, et al. Planning techniques for airport ground operations[C]//The 21st Digital Avionics Systems Conference. Piscataway, NJ, USA: IEEE, 2002: 1-12. |
| [11] | Garcia J, Berlanga A, Molina J M, et al. Optimization of airport ground operations integrating genetic and dynamic flow management algorithms[J]. AI Communications, 2003, 18(2): 143-164. |
| [12] | Pesic B, Durand N. Aircraft ground traffic optimization using a genetic algorithm[C]//The Genetic and Evolutionary Computation Conference. Piscataway, NJ, USA: IEEE, 2001: 1-9. |
| [13] | Gotteland J, Durand N, Alliot J M, et al. Aircraft ground traffic optimization[C]//The Genetic and Evolutionary Computation Conference. Piscataway, NJ, USA: IEEE, 2001: 1-9. |
| [14] | 王艳军, 胡明华, 苏炜. 基于冲突回避的动态滑行路径算法[J]. 西南交通大学学报, 2009, 44(6): 933-939. Wang Y J, Hu M H, Su W. Dynamic taxiway routing algorithm based on conflict avoidance[J]. Journal of Southwest Jiaotong University, 2009, 44(6): 933-939. |
| [15] | 汤新民, 王玉婷, 韩松臣. 基于DEDS的A-SMGCS航空器动态滑行路径规划研究[J]. 系统工程与电子技术, 2010, 32(12): 2669-2675. Tang X M, Wang Y T, Han S C. Aircraft dynamic taxiway routes planning for A-SMGCS based on DEDS[J]. Systems Engineering and Electronics. 2010, 32(12): 2669-2675. |
| [16] | 朱新平, 汤新民, 韩松臣. 基于Petri网与遗传算法的航空器滑行初始路径规划[J]. 西南交通大学学报, 2013, 48(3): 565-573. Zhu X P, Tang X M, Han S C. Aircraft initial taxiing route planning based on Petri net and genetic algorithm[J]. Journal of Southwest Jiaotong University, 2013, 48(3): 565-573. |
| [17] | 王化冰. 一种基于同步合成Petri网的FMS建模方法[J]. 系统工程理论与实践, 2001, 21(2): 35-42. Wang H B. A Petri net synchronous synthesis method for modeling flexible manufacturing systems[J]. System Engineering Theory and Practice, 2001, 21(2): 35-42. |
| [18] | 李茂军, 朱陶业, 童调生. 单亲遗传算法与传统遗传算法的比较研究[J]. 系统工程, 2001, 19(1): 61-65. Li M J, Zhu T Y, Tong T S. Comparison between partheno-genetic algorithm and traditional genetic algorithm[J]. Systems Engineering, 2001, 19(1): 61-65. |
| [19] | 李茂军, 罗日成, 童调生. 单亲遗传算法的遗传算子分析[J]. 系统工程与电子技术, 2001, 23(8): 84-87. Li M J, Luo R C, Tong T S. Analysis on the genetic operators of partheno-genetic algorithm[J]. Systems Engineering and Electronics, 2001, 23(8): 84-87. |
| [20] | 熊杰, 张晨. 基于飞机滑行油耗的枢纽机场机位分配研究[J]. 交通运输系统工程与信息, 2010, 10(3): 165-170. Xiong J, Zhang C. Airport gate assignment with airplane taxiing cost analysis[J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10(3): 165-170. |



