2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
在自然场景中满足矩形约束的图案很常见,比如日常生活中的地砖、 门框、 窗户、 桌子等. 图 1中的柜子、 抽屉都是矩形图案,这些图案满足矩形约束但往往长宽比是未知的. 由于相机拍摄并非垂直于矩形图案,因此图片中的矩形图案的长宽比不能反映矩形的真实长宽比. 本文提出一种算法可以利用单幅图像中矩形4个顶点对应的像点,有效地估计出矩形长宽比,同时可以给出矩形目标跟相机的相对位姿.
通过测量空间中N个点以及对应像点来获取相机的相对位姿是计算机视觉中的常见问题,这也就是所谓PNP(perspective-n-point)问题[1]. 通常PNP问题,对应点数目有很多[2](4~50个点),对应点越多获得的相机位姿估计就越准确[3]. 对应点大于5个时通常采用DLT(direct linear transformation)法进行求解[4],对应点为4个或5个时,通常采用基于代数方法求解,根据对应点的分布情况可能存在多解. 文[5, 6]给出了对应点为4个时的解法,文[2]和文[7]给出了对应点为5个时的解法. 在PNP问题中由于对应点的空间坐标需要通过事先测量来确定,但是在通常的自然场景中(如图 1),可以看出获取任意点的空间坐标是很难的,这限制了PNP问题在自然场景中的应用. 为了解决这个困难,我们利用自然场景中的矩形先验知识来构建坐标系从而确定矩形顶点的空间坐标,但是由于矩形长宽比是未知的,矩形顶点的空间坐标还是不能完全确定. 这种不确定性会很大程度上影响位姿求解的精度,所以该问题不能通过通常的PNP算法解决. Haralick最早给出此类问题的代数解法[8],高学海等人[9]在此基础上提出了利用解方程的思想求解长宽比进而求解相对位姿. 由于位姿(6DOF)和矩形长宽比(1DOF)未知,所以总共有7个未知量. 该方法利用图像中已知4个顶点及其像点的对应关系建立8组方程,通过解方程的方法得到长宽比和位姿. 该算法在不存在误差的前提下可以给出比较理想的解,但是当存在误差时给出的解会有很大偏差. 原因是高学海等人的算法只使用7组方程来求解,由于前7组求解时没有考虑误差存在,所有的误差都会累计到第8组方程上,造成解很大程度上偏离第8组方程. 翟坤等人[10]在高学海等人算法的基础上给出了基于坐标转换矩阵的推导方式,由于还是利用了解方程的思想,得到的结果需要额外滤波处理来减少误差. 基于以上分析,本文采用基于非线性优化的方法来解决这些不足,在位姿矩阵的表示上没有采用通常的欧拉角和单位四元数表示法[11, 12],而是利用了李群的理论[13]. 近些年来发展起来的基于流形和李群的优化算法非常高效[14],如文[15, 16]中应用李群的表示来估计帧间相机的移动得到了高效的算法. 经过试验表明,利用李群表示法优化目标函数不但可以快速收敛而且结果对初值的依赖并不明显,即可以很大范围内收敛到最优解.

|
| 图 1 典型办公室场景 Fig. 1 Typical office scene |
以矩形顶点作为原点,宽边作为x轴,长边作为y轴,根据右手定则选择z轴,建立世界坐标系. 设矩形的长宽比为τ,世界坐标系单位的选择不影响姿态求解,求解出的平移分量为世界坐标系单位下的数值. 简单起见选择宽边作为单位长度,这样矩形的顶点的坐标可以确定下来,这里采用齐次坐标表示:
p1: (0,0,0,1)T,p2: (1,0,0,1)T
p3: (1,τ,0,1)T,p4: (0,τ,0,1)T (·)T是向量转置. 设4×4矩阵T是从世界坐标系到相机坐标系的变换矩阵,这个矩阵由一个3×3旋转矩阵R和一个3×1平移分量t所组成,通常称矩阵T为欧几里得变换矩阵. K为相机矩阵,这两个矩阵的表达式为
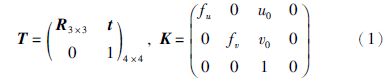
设ui是测量的矩形顶点对应的像点,u′i是根据相机成像公式计算出矩形顶点的像点,i=1,2,3,4,则有:
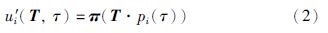
其中: π: R4→R2.
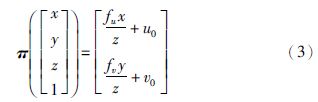
基于优化的求解算法变成对下面优化问题的求解
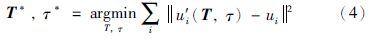
式(4)可以通过牛顿法或LM(Levenberg-Marquardt)法[17]进行迭代求解. 由于迭代过程中需要同时更新T和τ,实验中发现更新T和τ会彼此互相影响,造成算法收敛非常慢. 直观上原因也很好理解,因为长宽比对位姿影响非常大,迭代中位姿始终随长宽比迭代不断变动,而长宽比也由于位姿的变动难以收敛. 实验中还发现很多情况只能收敛到局部最优解.
上述分析启发我们,若想得到精度较高的解,必须分离T和τ彼此的相互影响. 为此,我们可以对τ离散化,对每个τ通过(5)式计算投影误差,选取投影误差最小τ*作为长宽比的估计式.
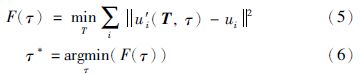
τ固定时,需要求解的只有T. 迭代求解T时需要对旋转矩阵进行参数化表示. 常用的旋转矩阵表示方法有: 矩阵表示、 欧拉角表示、 单位四元数表示. 使用矩阵表示原优化问题变成线性问题,可以通过最小二乘法来进行求解. 但是由于矩阵表示需要有9个参数,所以这种方法并不适用于对应点较少的情况. 采用欧拉角表示旋转矩阵只需要3个参数,但是由于需要计算三角函数,容易产生数值不稳定; 更坏的是由于三角函数是非凸的,即使原问题是凸的,采用三角函数后也会破坏原问题的凸性,造成结果非常依赖初值的选定. 采用单位四元数表示方法,由于迭代求解过程中需要同时满足单位四元数的约束,而单位四元数的约束无论是加入到每次牛顿法或LM法迭代中进行归一化或者加入到目标函数中都会影响收敛速度. 这里我们采用基于李群的方法表示旋转矩阵R和平移向量t.
实验结果表明,在这种表示下优化结果对于初值的选取并不敏感,可以在很大范围收敛到最优值.
李群满足光滑流形和群两个性质[13]. 三维欧几里得变换满足李群条件,构成的李群通常被记作SE(3),群中的单位元记作e. 李群通常不是线性的,在局部上可以通过投影到切空间进行线性化. 由于李群从整体上并不是线性的,所以不同点的切空间是不同的. 需要指出的是由于李群满足群的性质,一个重要结论就是不同点切空间可以由e处的切空间确定. 我们这里对李群下面的推导都是只需要在e处的切空间Ve. 设ξ(ξ1,ξ2,ξ3,ξ4,ξ5,ξ6)T属于SE(3)在e点处的切空间Ve,ξ是6维向量,前3维对应平移,后3维对应旋转. 指数映射是从切空间到李群的映射,式(7)定义从ξ到SE(3)的指数映射.
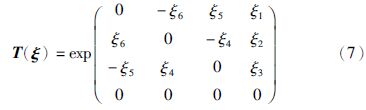
e点附近T(ξ)对ξ的导数可以紧凑地记作:
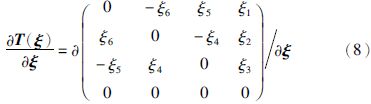
利用上述表示法进行推导用于高斯牛顿法的迭代公式:
1) 对E(ξ)线性化
设T是对T的估计,T(ξ)·T是真实变换矩阵,求解ξ
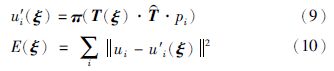
对ui-u′i(ξ)做一阶展开,Ji是对应的雅可比矩阵
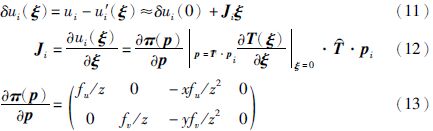
把式(11)代入式(10)式得到
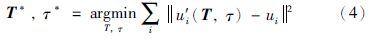
2) 对E(ξ)线性化后是ξ的线性函数,通过对ξ求导可以求出E(ξ)的最小值
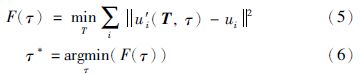
3) 求出的ξ作为更新量,更新T
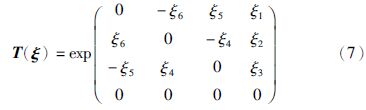
上述方法迭代非常有效,通常经5~6步即可完成迭代,而且每步迭代的计算量也很小. LM法加入阻尼项以保证迭代中每步代价函数都能下降,但是阻尼项也会同时影响二阶收敛速度[19]. 实验中发现在李群表示下LM法要慢于高斯牛顿法,所以没有采用LM法.
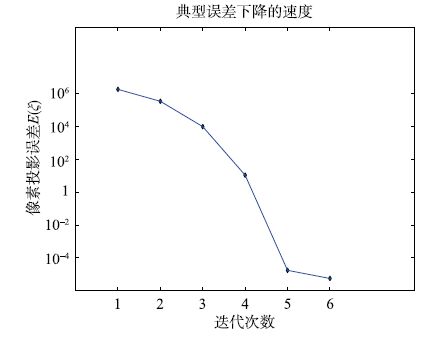
图 2是在长宽比为1时,从初值(欧拉角(0,0,0)T,平移(0,0,1)T)收敛到真实值(欧拉角(11.46°,17.19°,17.19°)T,平移(0.307,0.099,0.667)T)时的误差下降曲线.
|
| 图 2 高斯牛顿法误差曲线 Fig. 2 Error curve using Gauss-Newton method |
从图 2中可以看出误差从106下降到10-4只用了6步,每步以2位有效数字速度下降,验证了算法非常高效.
2.3 求解长宽比τ由于通常被测量矩形的长宽比在一定范围内,不失一般性,我们设被测量矩形的长宽比在0.1到10之间. 通过对长宽比离散采样的方法可以得到一定精度的长宽比的估计. 例如,在0.1到10之间,均匀采样2 000次,利用2.2节的算法,得到每个τ对应的像素误差F(τ),取其中的F(τ)最小值可以得到0.005精度的估计. 由于2.2节的算法非常高效,在PC(CPU Intel Core i5-3470 3.20 GHz,内存为4 G)上实测,对τ离散采样2 000次后进行估计耗时只有0.01 s(±0.001 s).
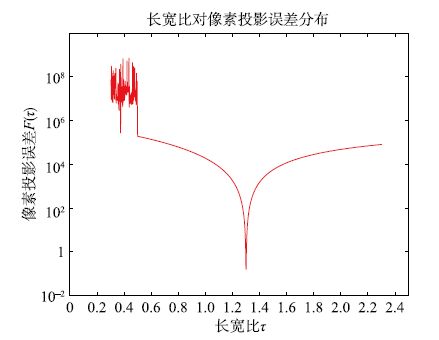
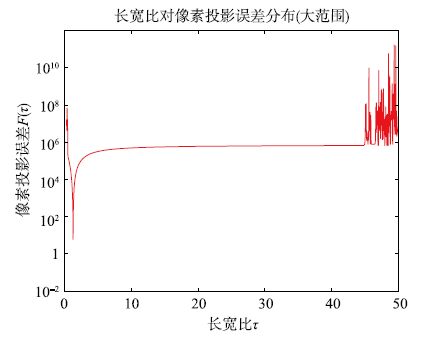
图 3是在τ真实值为1.3时,通过对τ进行2 000次均匀采样绘制出的τ和F(τ)的曲线图. 从图 3可以看出F(τ)符合拟凸函数的曲线,在真实值处F(τ)最小,真实值两侧一定范围内逐渐增加,离真实值很远处由于迭代没有收敛所以开始震荡. 图 4是τ从0到50采样绘制的τ和F(τ)的曲线图,可以看出即使是在更大范围内F(τ)依然表现出拟凸函数的特征[18].
|
| 图 3 长宽比和像素投影误差关系 Fig. 3 The relationship between the aspect radio and the projective error |
|
| 图 4 长宽比和像素投影误差关系(大范围) Fig. 4 The relationship between the aspect radio and the projective error (large scale) |
拟凸函数可以通过二分搜索法快速求解最小值. 通过二分搜索法可以得到精度更高的τ值. 设计算法如下:
1) 先对τ进行均匀采样得到一组F(τ). F(τ)小于阈值104作为拟凸函数最小值区间,记为[a,b].
2) 判断最小值区间中点(a+b)/2处导数的升降,如果导数上升,最小值区间设为[a,(a+b)/2]; 如果下降,最小值区间设为[(a+b)/2,b]. 这里通过计算的中点及其邻近一点的F(τ)数值来判断升降.
3) 重复进行步骤2)从而不断缩小最小值区间,直到最小值区间的长度小于事先设定的阈值0.000 5.
3 实验结果与分析实验使用的PC的CPU配置为Intel Core i5-3470 3.20 GHz,内存为4 G. 实验采用Kinect2[12]作为相机采集图像,表 1是相机参数以及标定后的内参数.
| 图像尺寸 | fu | fv | u0 | v0 |
| 1 920×1 080 | 1 109.671 | 1 108.866 | 963.175 | 533.347 |
为了验证算法有效性和实时性,设计以下3个实验. 实验1参考文[9]的实验方法,在仿真条件下验证算法位姿计算的有效性. 实验2和实验3在存在噪声条件下进行验证,这里没有模拟噪声而是直接在真实场景下进行算法验证,因为这样可以更好地验证算法的实用性.
3.1 实验1实验1根据相机成像式(2),从实验模型计算出矩形顶点的像点坐标. 用矩形顶点的像点坐标作为算法输入计算位姿,跟实验模型中的位姿进行比较. 为了比较结果方便,位姿用欧拉角方式给出. 欧拉角采用x-y-z方式(先沿x轴转再沿y轴最后z轴),picth为按x轴旋转角度,roll按y轴旋转角度,yaw按z轴旋转角度. 实验结果如表 2所示,这里可以看出在无噪声时算法计算的位姿跟实验模型的位姿是一致.
| 实验模型 | 算法输入 | 算法输出 | ||||
| 旋转角度/(°) | 平移/mm | 矩形尺寸/mm | 矩形顶点像点坐标 | 旋转角度/(°) | 平移/mm | 长宽比 |
| pitch=20 roll=15 yaw=10 | x=-15 y=25 z=-1 000 | L=200 W=100 | (946.53,561.069) (1 168.26,601.811) (1 152.76,705.818) (938.899,661.167) | pitch=20.000 4 roll=14.999 6 yaw=10.000 0 | x=-15.000 5 y=24.999 5 z=-999.999 0 | τ=2.00 |
| pitch=-25 roll=15 yaw=-30 | x=20 y=-30 z=-1 500 | L=240 W=100 | (948.38,555.525) (806.353,636.922) (785.534,576.205) (922.959,494.517) | pitch=-25.000 0 roll=15.000 0 yaw=-30.000 0 | x=20.000 8 y=-29.999 4 z=-1 500.010 0 | τ=2.40 |
实验2用来验证算法测量自然场景中矩形长宽比的有效性. 如图 1所示,选取办公室场景作为待测自然场景,选取办公柜的一扇柜门为待测矩形,红色圆点标出待测矩形4个顶点,4个顶点的像素值见表 3.
| 柜门顶点像点坐标 | 点1 | 点2 | 点3 | 点4 |
| U | 969 | 713 | 738 | 967 |
| V | 663 | 675 | 166 | 106 |
通过实际测量得到柜门长为40.8 cm,高为83.4 cm,真实长宽比为0.489 2. 通过本文算法测定柜门长宽比为0.483 5,所以算法相对估计误差为1.17%. 这里的误差可能是由于给定的矩形顶点像点只精确到像素级造成的.
3.3 实验3实验3通过处理实时视频用来验证算法的实时性和鲁棒性. 如图 5所示,选取棋盘格的顶点作为被测矩形,通过Kinect2采集视频,在实验中将相机固定并不断改变棋盘格的姿态,通过本文算法实时估计长宽比、 投影错误和相对位姿. 相对位姿的计算结果通过投影世界坐标系的方式输出到图像中. 为了尽可能地模拟真实环境可能存在的误差,实验时大幅度快速移动棋盘格. 大幅度快速移动棋盘格会造成矩形顶点像点获取存在较大误差,可以用来测试算法的鲁棒性. 我们采用10×7的棋盘格进行实验. 棋盘格内部8×5的矩形区域作为被测量矩形,矩形长宽比的真实值为1.6.

|
| 图 5 实验结果 Fig. 5 Experimental result |
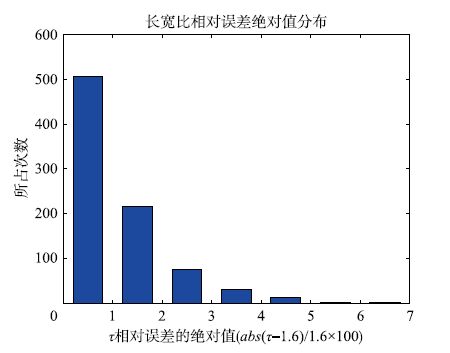
实验3共采集了53 s的视频,一共处理了841帧数据,平均每秒处理15帧数据. 图 6是长宽比相对误差绝对值的分布图,纵轴为出现次数. 其中长宽比相对误差在3%以内的为797次(占94.77%),长宽比相对误差在4%以内的为828次(占98.45%). 算法在实验3测试中有1.55%的结果稍大地偏离真实长宽比. 为了分析原因,这里选取了两幅长宽比相对误差大的代表性图像(图 7和图 8). 图 7为沿宽轴旋转70°,长轴旋转-51°,算法测量长宽比为1.707,比真实值要大6.6%; 图 8为沿宽轴旋转5°,沿长轴旋转-60°,算法测量长宽比为1.546,比真实值小3.4%. 在图 7中矩形其中一边离相机较另一边稍远,在图 8中矩形沿长轴旋转要远大于宽轴. 在这两种情况下,矩形顶点提取误差对长宽比计算影响并不是等权重的. 可以想象当矩形沿宽轴旋转接近90°时,矩形像点提取水平方向的误差对结果影响要远大于竖直方向的误差,所以需要根据姿态来调整目标函数(4)中误差的权重. 在接下来的研究中将考虑如何通过设计姿态和误差权重的关系来进一步提高长宽比求解的精度.
|
| 图 6 长宽比相对误差绝对值分布图 Fig. 6 Histogram of the absolute error of aspect radio |

|
| 图 7 误差较大的代表帧(长宽比过大) Fig. 7 A typical frame of larger absolute error (bigger aspect radio) |

|
| 图 8 误差较大的代表帧(长宽比过小) Fig. 8 A typical frame of larger absolute error (smaller aspect radio) |
本文采用非线性优化的方法解决矩形长宽比和位姿同时估计的问题. 通过把问题转换成优化问题,很容易通过增加多个对应点提高矩形长宽比估计的鲁棒性; 采用李群对优化问题中欧几里得变换矩阵进行表示得到了非常高效的求解算法; 通过分离矩形长宽比和位姿,消除了由于矩形长宽比和位姿都不确定对迭代速度的影响. 通过贴近真实环境的实验设计,验证了该算法有效性和实时性.
| [1] | Fishler M A, Bolles R C. Random sample consensus: A paradigm for model fitting with applications to image analysis and antomated cartographpy[J]. Communications of the ACM, 1981, 24(6): 381-395. |
| [2] | Lepetit V, Moreno-Noguer F, Fua P. EPnP: An accurate O(n) solution to the PnP problem[J]. International Journal Computer Vision(IJCV), 2009, 81(2): 155-166. |
| [3] | Quan L, Lan Z. Linear n-point camera pose determination[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(8): 774-780. |
| [4] | Abdel-Aziz Y I. Direct linear transformation from comparator coordinates in close-range photogrammetry[C]//ASP Symposium on Close-Range Photogrammetry in Illinois. Falls Church, VI, USA: American Society of Photogrammetry, 1971: 1-18. |
| [5] | 胡占义, 雷成, 吴福朝. 关于P4P问题的一点讨论[J]. 自动化学报, 2001, 27(6): 770-773. Hu Z Y, Lei C, Wu F C. A short note on P4P problem[J]. Acta Automatica Sinica, 2001, 27(6): 770-773. |
| [6] | 王鹏, 孙长库, 张子淼. 单目视觉位姿测量的线性求解[J]. 仪器仪表学报, 2011, 32(5): 1126-1131. Wang P, Sun C K, Zhang Z M. Linear pose estimation with a monocular vision system[J]. Chinese Journal of Scientific Instrument, 2011, 32(5): 1126-1131. |
| [7] | 吴福朝, 胡占义. 关于P5P问题的研究[J]. 软件学报, 2001, 12(5): 768-775. Wu F C, Hu Z Y. A study on the P5P problem[J]. Journal of Software, 2001, 12(5): 768-775. |
| [8] | Haralick R M. Determining camera parameters from the perspective projection of a rectangle[J]. Pattern Recognition, 1989, 22(3): 225-230. |
| [9] | 高学海, 徐科军, 张瀚, 等. 基于单目视觉和激光测距仪的位姿测量算法[J]. 仪器仪表学报, 2007, 28(8): 1479-1485. Gao X H, Xu K J, Zhang H, et al. Position-pose measurement algorithm based on single camera and laser range-finder[J]. Chinese Journal of Scientific Instrument, 2007, 28(8): 1479-1485. |
| [10] | 翟坤, 曲溪, 李志, 等. 非合作航天器相对姿态确定算法及地面试验[J]. 哈尔滨工业大学学报, 2014, 46(3): 61-65. Zhai K, Qu X, Li Z, et al. Ground test and relative attitude determination algorithms of non-cooperative spacecraft[J]. Journal of Harbin Institute of Technology, 2014, 46(3): 61-65. |
| [11] | 李洁, 丁全心, 王鹏. 基于四元数的单目视觉物体位姿测量方法[J]. 航空计算技术, 2011, 41(6): 16-19. Li J, Ding Q X, Wang P. Monocular vision measurement method of object position and orientation based on quaternions[J]. Aeronautical Computing Technique, 2011, 41(6): 16-19. |
| [12] | 王君臣, 王田苗, 杨艳, 等. 非线性最优机器人手眼标定[J]. 西安交通大学学报, 2011, 45(9): 15-20. Wang J C, Wang T M, Yang Y, et al. Nonlinear optimal robot hand-eye calibration[J]. Academic Journal of Xi'an Jiaotong University, 2011, 45(9): 15-20. |
| [13] | Boothby W M. An introduction to differentiable manifolds and riemannian geometry[M]. New York, USA: Academic Press, 1975. |
| [14] | Absil P A, Mahony R, Sepulchre R. Optimization algorithms on matrix manifolds[M]. Princeton, USA: Princeton University Press, 2008. |
| [15] | Forster C, Pizzoli M, Scaramuzza D. SVO: Fast semi-direct monocular visual odometry[C]//International Conference on Robotics and Automation (ICRA). Piscataway, NJ, USA: IEEE, 2014: 15-22. |
| [16] | Engel J, Schops T, Cremers D. LSD-SLAM: Large-scale direct monocular SLAM[C]//European Conference on Computer Vision (ECCV). Zurich, Switzerland: Springer, 2014: 834-849. |
| [17] | Nocedal J, Wright S J. Numerical Optimization[M]. 2nd ed. New York, USA: Springer, 2006. |
| [18] | Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge, England: Cambridge University Press, 2004. |
| [19] | Triggs W, McLauchlan P, Hartley R, et al. Bundle adjustment: A modern synthesis[C]//Proceedings of International Workshop on Vision Algorithms. London, UK: Springer-Verlag, 1999: 298-372. |
| [20] | Kinect for Windows[EB/OL]. (2015-01-01)[2015-04-26]. http://www. microsoft. com/en-us/kinectforwindows/develop/. |



