1 引言
航天器编队飞行指若干个航天器组成某种构型,协同执行空间科学任务. 相比单体航天器,航天器编队鲁棒性更强、 观测精度更高、 可靠性更好. NASA (National Aeronautics and Space Administration)、 ESA (the European Space Agency)等航空航天研究机构对深空编队飞行给予了密切关注,并分别制定了Darwin、 TPF (the terrestrial planet finder)等平动点轨道编队飞行计划[1].
日心悬浮轨道是航天器推进力与太阳引力相互平衡形成的悬浮在太阳上方区域的非开普勒周期轨道,其特殊的空间位置为深空通信、 日地观测等任务提供了理想平台[2]. 因此,对于高分辨率深空探测、 深空通信中转基站等重大航天工程,基于日心悬浮轨道的航天器编队飞行具有巨大的应用前景. 值得注意的是,上述任务的特点对编队飞行精度提出了较高要求. 参考NASA制定的编队飞行任务标准,编队飞行控制精度需要达到5 mm量级[3].
由于航天器轨道动力学方程具有强耦合、 非线性的特点,因此将航天器轨道动力学方程在标称轨道附近线性化后进行分析研究是当前设计编队飞行控制器较为普遍的方法. Peng等[4]针对线性周期时变平动点轨道动力学方程提出了最优周期控制器. Kulkarni等[5]基于离散LTV (linear time variant)模型设计了H∞控制器,实现了日地L1点Halo轨道的编队飞行控制. 然而,基于局部线性化动力学方程设计的编队飞行控制方法有效范围存在约束,同时考虑到获取精确的系统模型不仅难度较大,而且模型参数会随着航天器工况及深空环境的变化产生漂移,因此基于局部线性化模型的控制系统鲁棒性也难以令人满意. 此外,线性化方法处理非线性系统控制问题时仅能保证局部稳定且一般情况下很难求出吸引区[6]. 出于上述原因,部分学者基于非线性动力学模型设计编队飞行控制器. Rahmani等[7]采用最优控制理论和极值变分方法解决了Halo轨道编队飞行控制问题. Gurfil等[1]提出了平动点轨道自适应神经网络编队飞行控制方法. 但是,以上方法同样依赖于非线性系统模型,而且非线性控制方法增加了控制器的实现复杂度.
对于日心悬浮轨道编队飞行控制问题,Gong等[8, 9, 10]通过分析线性化相对运动方程讨论了LQR与IFL编队控制方法. 值得注意的是,文[8, 9, 10]推导航天器轨道动力学方程时并未考虑地球引力和扰动因素且设计的控制策略仅能保证编队系统稳定,难以达到较高的编队飞行精度.
针对上述不足,本文对日心悬浮轨道编队飞行控制展开了进一步研究. 首先,考虑地球引力及地球轨道偏心率扰动等因素,推导了航天器编队日心悬浮轨道动力学方程. 与文[8, 9, 10]相比,本文建立的动力学模型更符合实际运行环境. 其次,应用线性自抗扰控制技术,提出一种基于系统输入输出而不依赖精确系统模型的日心悬浮轨道编队飞行控制策略. 本文设计的控制算法结构简单、 计算量小,具有较强的鲁棒性和抗干扰性,克服了航天器轨道动力学方程的强耦合、 非线性问题,同时避免了现有编队飞行控制方法存在的模型依赖、 控制器有效性约束等缺陷. 最后,通过数值仿真验证了存在入轨误差、 扰动和模型不确定性时,所设计的控制方法能够实现高精度的日心悬浮轨道编队飞行控制.
2 航天器编队日心悬浮轨道动力学方程航天器编队大致可以分为3种构型: 主从式、 行为式和虚拟结构式,其中主从式构型结构清晰、 易于实现[4]. 因此,本文针对主从式航天器编队飞行展开讨论. 主要考虑两航天器编队,多航天器编队飞行分析方法类似.
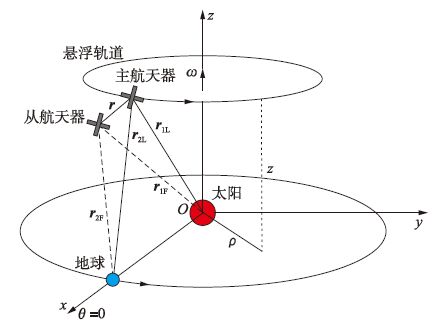
2.1 主航天器日心悬浮轨道动力学方程McInnes[11, 12]、 Gong[8, 9, 10]、 钱航[13]基于二体模型推导了太阳帆航天器日心悬浮轨道动力学方程. 但事实上,在太阳、 地球和航天器组成的系统中,仅当航天器距离地球足够远时,才能够忽略地球引力. 因此,采用三体模型研究航天器的运动更为合理. 基于分析航天器深空轨道运动广泛采用的圆形限制性三体问题模型[14],建立日心悬浮轨道坐标系如图 1所示.
|
| 图 1 日心悬浮轨道坐标系 Fig. 1 Heliocentric displaced orbit reference frame |
坐标原点O为日心,x轴指向J2000星历的春分点,z轴指向地球公转的角速度方向,x、 y、 z三轴组成右手坐标系; ρ、 z分别为悬浮轨道的半径和高度,主航天器以角速度ω在悬浮轨道上运行. 主航天器轨道动力学方程为
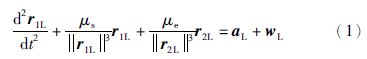
为简化分析,采用归一化单位,定义日地距离(AU)为单位长度,太阳质量为单位质量,地球公转角速度为单位角速度,则μs=1,μe=3.003 490×10-6,主航天器轨道动力学方程表示为
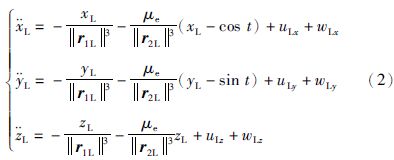
与主航天器轨道动力学方程推导过程类似,从航天器轨道动力学方程表示为
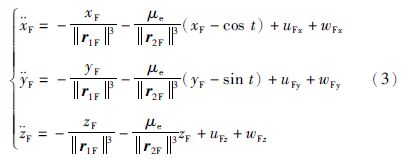
式中,r1F=[xFyFzF]T为从航天器在悬浮轨道坐标系下的位置矢量,r2F为从航天器相对地球的位置矢量,aF=[uFxuFyuFz]T为从航天器推进加速度,wF=[wFxwFywFz]T为从航天器扰动加速度.
定义从航天器相对主航天器的位置向量r=[XYZ]T,则r=r1F-r1L. 由式(2)、 (3)可得从航天器相对运动动力学方程为
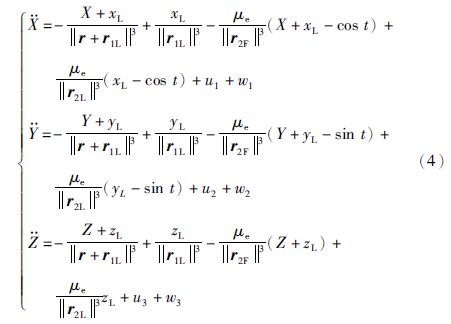
3 编队飞行控制器设计
自抗扰控制[15](active disturbance rejection control,ADRC)是一种基于系统输入输出而不依赖系统模型的控制方法,
在航天航空领域,自抗扰控制技术已成功应用于飞行器导航制导、 航天器姿态控制[16, 17]. 高志强[18]利用带宽思想,进一步提出了线性自抗扰控制方法(linear active disturbance rejection control,LADRC). 该方法继承了自抗扰控制技术的优良性能,参数整定更为简便,且大量研究表明LADRC对复杂的非线性不确定对象同样具有很好的控制效果[19].
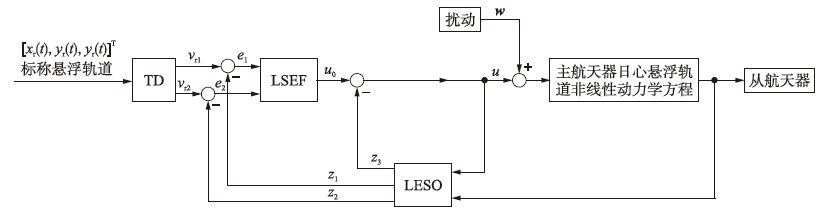
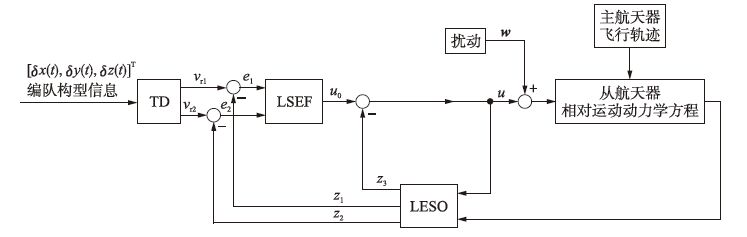
根据上节推导的航天器编队日心悬浮轨道动力学方程,本节基于LADRC设计了主航天器轨道保持控制器及编队飞行控制器,结构如图 2、 3所示,其中vr1为标称轨道位置信息或编队构型信息的跟踪信息,vr2为vr1的微分信息,u0为状态误差反馈控制量,u为经过扰动补偿后的最终控制量. 主航天器轨道保持控制器实现主航天器对标称悬浮轨道的跟踪保持,确保编队稳定在悬浮轨道附近执行航天任务. 编队飞行控制器实现从航天器对主航天器的跟踪,以保持高精度的期望编队构型. 从控制器结构图 2、3可以看出,主航天器轨道保持控制器与编队飞行控制器可以分别独立进行设计,因此本节重点讨论编队飞行控制器设计,主航天器轨道保持控制器设计过程类似.
|
| 图 2 主航天器线性自抗扰轨道保持控制器结构图 Fig. 2 Block diagram of the linear active disturbance rejection controller for the leader spacecraft |
|
| 图 3 线性自抗扰编队飞行控制器结构图 Fig. 3 Block diagram of the linear active disturbance rejection controller for the spacecraft formation |
定义状态变量xi1(i=1,2,3)表示从航天器相对主航天器的位置向量的三轴分量,方程(4)可表示为
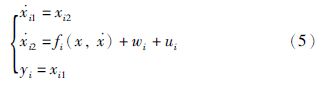
本文利用跟踪微分器安排过渡过程,并获取其微分信号. 假设仅位置信息可测,离散跟踪微分器为
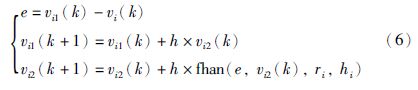
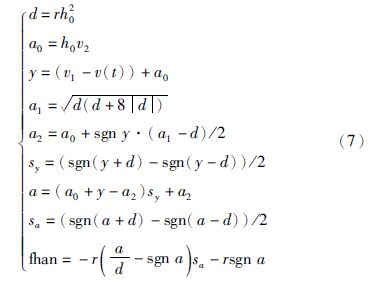
线性扩张状态观测器用于估计对象的状态及系统建模不确定性与未建模扰动. 定义F(x,${\dot x}$)=f(x,${\dot x}$)+w,其中w=[w1w2w3]T,事实上,从反馈控制角度看,F(x,${\dot x}$)需要通过控制量进行补偿,因此可以视为“总扰动”. 将F(x,${\dot x}$)增广为状态变量,记为

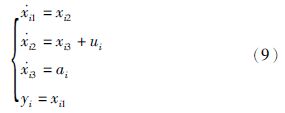
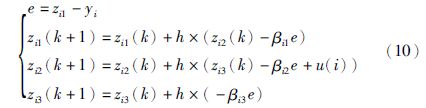
3.2节设计的离散线性扩张状态观测器实现了对系统建模不确定性和扰动的观测,因此可以在反馈控制中进行补偿. 设计离散线性状态误差反馈控制律为
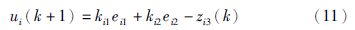
在深空环境中,航天器面临星体引力、 执行机构非线性等各类扰动. 对于日地圆形限制性三体问题模型,地球轨道偏心率扰动和月球引力为最主要的扰动因素,其中地球轨道偏心率扰动影响最为显著[4, 5]. 因此,为了验证本文设计的编队飞行控制器的抗干扰性能,考虑地球轨道偏心率扰动. 单位质量航天器受到的地球轨道偏心率扰动可近似表示为[4, 5]
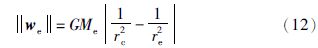
当前,世界各航天大国相继启动了火星探测工程. 然而,由于太阳的掩星效应,地面与火星表面及环绕火星运行的航天器无法持续通信,地球—火星通信中继示意图[2, 20]如图 4所示.
|
| 图 4 火星—地球通信中继示意 Fig. 4 The diagram of Mars-Earth communication relay |
假设依托日心悬浮轨道通信中继卫星编队实现地球与火星的不间断通信,无量纲的标称悬浮轨道参数如表 1所示.
采用MAXIM Path′s finder任务中使用的直线编队[1],即主、 从航天器入轨后相互分离,主航天器在标称轨道上运行,从航天器跟随主航天器飞行并保持设定距离. 假设主、 从航天器相对位置为[100 km,100 km,0]T.
目前,太阳帆技术仍处于理论研究阶段,因此采用已经成熟应用于航天任务的太阳电推进技术. 选择Qinetiq T6型号[20]太阳电推进器,该推进器可提供最大幅值230 mN的推力.
假定初始入轨误差为250 km,航天器质量为200 kg. 设定仿真步长为0.000 1 TU (1 TU≈58 d),仿真时间为900 d.
4.1 主航天器轨道保持控制设置主航天器自抗扰轨道保持控制器参数如表 2所示.
| TD | LESO | LSEF |
| r1=1 000 | β11=80 β12=1 000 β13=6 000 | k11=1 000 000 k12=2 000 |
| r2=1 000 | β21=100 β22=1 000 β23=4 000 | k21=500 000 k22=2 000 |
| r3=1 000 | β31=100 β32=1 000 β33=4 000 | k31=1 000 k32=200 |
图 5给出了主航天器日心悬浮轨道自抗扰保持控制结果. 图 5(a)中实线为标称轨道,虚线为实际运行轨迹,两者重合度表明轨控精度良好. 由图 5(b)可知,初始入轨误差经过100 d后收敛至0.5 km范围内,速度误差经过50 d后收敛至0.05 m/s范围内,控制量在30 d后保持稳定.
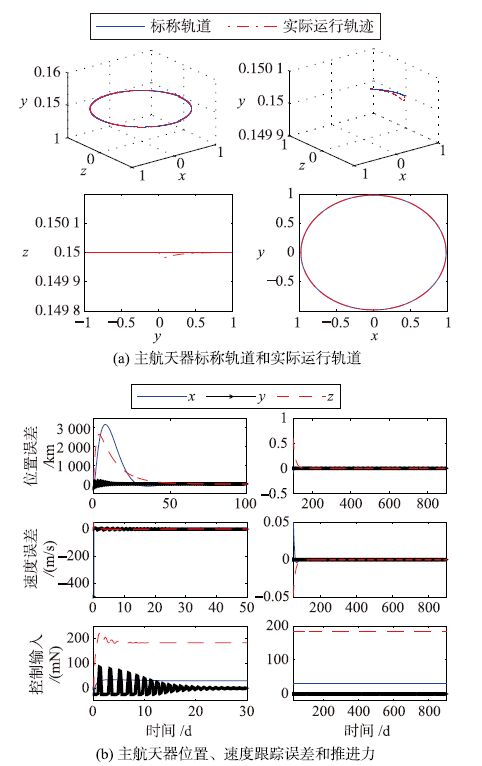
|
| 图 5 主航天器日心悬浮轨道保持控制结果 Fig. 5 Station-keeping control results of heliocentric displaced orbit for leader spacecraft |
为了更精确地描述航天器进入稳态后长期运行的轨控精度,采用应用较普遍的评价参数[4]——绝对位置误差均值,表达式为
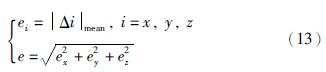
| ex /km | ey /km | ez /km | e /km |
| 3.568 8e-04 | 0.001 3 | 0.018 8 | 0.018 8 |
设置自抗扰编队飞行控制器参数如表 4所示.
| TD | LESO | LSEF |
| r1=1 000 | β11=2 400 β12=160 000 β13=64 000 000 | k11=160 000 k12=3 000 |
| r2=1 000 | β21=600 β22=5 000 β23=20 000 | k21=20 000 k22=1 000 |
| r3=1 000 | β31=300 β32=2 500 β33=12 500 | k31=2 500 k32=200 |
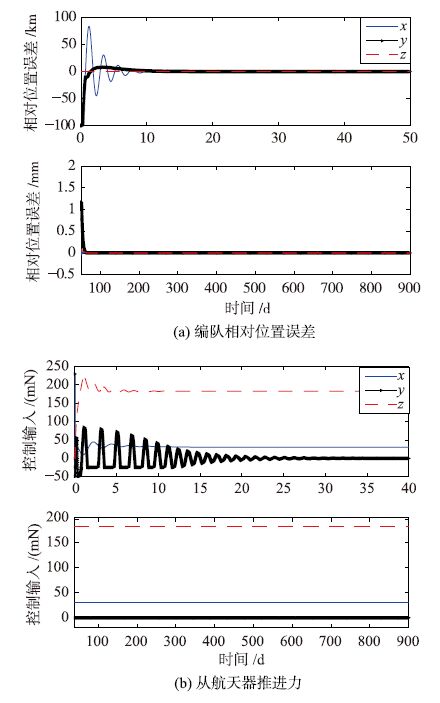
图 6为自抗扰编队飞行控制结果,表明主、 从航天器入轨相互分离后,经过50 d实现了编队重构,相对位置误差由初始的100 km收敛至2 mm范围内,超过了NASA制定的编队飞行精度标准(5 mm). 编队飞行控制精度如表 5所示.
|
| 图 6 编队飞行控制结果 Fig. 6 Control results of spacecraft formation flying |
| ex /mm | ey /mm | ez /mm | e /mm |
| 2.672 6e-04 | 0.009 2 | 0.001 4 | 0.0093 |
本文研究了基于线性自抗扰技术的航天器日心悬浮轨道编队飞行控制器设计方法. 首先,考虑外部扰动建立了更符合实际运行环境的航天器轨道动力学模型. 进而,设计了一种基于系统输入输出而不依赖精确系统模型的编队飞行控制策略,克服了航天器轨道动力学方程的强耦合、 非线性问题,同时避免了现有编队飞行控制方法存在的模型依赖、 控制器有效性约束等缺陷. 数值仿真验证了存在初始入轨误差、 扰动因素及系统模型不确定性的情况下,所设计的控制器能够实现5 mm精度的编队飞行控制.
应当指出,本文设计的自抗扰编队飞行控制器结构简单、 计算量小,且仅需掌握系统的输入、 输出信息,即传感器测量的发动机推力及航天器位置信息,而并非难以获取的全部状态信息以及精确的模型信息,因此相比其它控制方法更易于工程实现. 但是,为了使自抗扰编队飞行控制器达到令人满意的控制效果,需要花费大量时间反复调节控制器参数. 因此,如何快速简便的获取最优自抗扰控制器参数值得进一步探索.
| [1] | Gurfil P, Idan M, Kasdin N J. Adaptive neural control of deep-space formation flying[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(3): 491-501. |
| [2] | McKay R, Macdonald M, Biggs J, et al. Survey of highly non-Keplerian orbits with low-thrust propulsion[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 645-666. |
| [3] | Beichman C. Terrestrial planets finder[J]. Bulletin of the American Astronomical Society, 1999, 31(4): 1119. |
| [4] | Peng H J, Zhao J, Wu Z G, et al. Optimal periodic controller for formation flying on libration point orbits[J]. Acta Astronautica, 2011, 69(7): 537-550. |
| [5] | Kulkarni J E, Campbell M E, Dullerud G E. Stabilization of spacecraft flight in halo orbits: An H∞approach[J]. IEEE Transactions on Control Systems Technology, 2006, 14(3): 572-578. |
| [6] | 张辉, 朱敏, 周建亮, 等. 姿态角幅值约束下的太阳帆Lissajous轨道保持控制[J]. 空间科学学报, 2014, 34(6): 872-880. Zhang H, Zhu M, Zhou J L, et al. Station-keeping control of solar sail Lissajous orbit with attitude angles amplitude constraint[J]. Chinese Journal of Space Science, 2014, 34(6): 872-880. |
| [7] | Rahmani A, Jalali M A, Pourtakdoust S H. Optimal approach to halo orbit control[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Los Angeles, CA, USA: AIAA, 2003: 11-14. |
| [8] | Gong S P, Baoyin H X, Li J F. Solar sail formation flying around displaced solar orbits[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(4): 1148-1152. |
| [9] | Gong S P, Baoyin H X, Li J F. Relative orbit design and control of formation around displaced solar orbits[J]. Aerospace Science and Technology, 2008, 12(2): 195-201. |
| [10] | 龚胜平. 太阳帆航天器动力学与控制研究[D]. 北京: 清华大学, 2009. Gong S P. Study on dynamics and control of sail-craft[D]. Beijing: Tsinghua University, 2009. |
| [11] | McInnes C R. Passive control of displaced solar sail orbits[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(6): 975-982. |
| [12] | McInnes C R. The existence and stability of families of displacement two-body orbits[J]. Celestial Mechanics and Dynamical Astronomy, 1997, 67(2): 167-180. |
| [13] | 钱航, 郑建华, 于锡峥, 等. 太阳帆航天器悬浮轨道动力学与控制[J]. 空间科学学报, 2013, 33(4): 458-464. Qian H, Zheng J H, Yu X Z, et al. Dynamics and control of displaced orbits for solar sail spacecraft[J]. Chinese Journal of Space Science, 2013, 33(4): 458-464. |
| [14] | 刘林, 候锡云. 深空探测器轨道力学[M]. 北京: 电子工业出版社, 2012: 50-51. Liu L, Hou X Y. Dynamics in deep space exploration[M]. Beijing: Publishing House of Electronic Industry, 2012: 50-51. |
| [15] | 韩京清. 自抗扰控制及其应用[J]. 控制与决策, 1998, 13(1): 19-23. Han J Q. Active disturbance rejection controller and its applications[J]. Control and Decision, 1998, 13(1): 19-23. |
| [16] | 薛文超, 黄朝东, 黄一. 飞行制导控制一体化设计方法综述[J]. 控制理论与应用, 2013, 30(12): 1510-1519. Xue W C, Huang C D, Huang Y. Design methods for the integrated guidance and control system[J]. Control Theory and Applications, 2013, 30(12): 1510-1519. |
| [17] | 吴忠,黄丽雅,魏孔明,等. 航天器姿态自抗扰控制[J]. 控制理论与应用,2013,30(12): 1616-1621. Wu Z,Huang L Y,Wei K M,et al. Active disturbance rejection control of attitude for spacecraft[J]. Control Theory and Applications,2013,30(12): 1616-1621. |
| [18] | Gao Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference. Piscataway,NJ,USA: IEEE,2003: 4989-4996. |
| [19] | 黄一,薛文超,杨晓霞. 自抗扰控制: 思想、理论分析及运用[C]//第29届中国控制会议论文集. 皮斯卡塔韦,新泽西,美国: 电气电子工程师协会,2010: 6083-6090.Huang Y,Xue W C,Yang X X. Active disturbance rejection control: Methodology,Theoretical Analysis and Applications[C]//Proceedings of the 29th Chinese Control Conference. Piscataway,NJ,USA: IEEE,2010: 6083-6090. |
| [20] | McKay R J,Macdonald M,de Bosquillon F F,et al. Non-keplerian orbits using low thrust,high ISP propulsion systems[C]//60th International Astronautical Congress. 2009: C1.2.8. |



