1 引言
随着网络服务需求的快速增长,在高速网络中,实时网络流量的有效分配目前已引起研究者的广泛关注. 为了在网络终端用户间恰当地动态分配带宽,发展适用的流量管理策略,利用预测网络流量[1, 2, 3, 4, 5]来分配网络资源有助于满足网络服务质量(quality of service,QoS)要求. 与此同时,鉴于多媒体应用对网络流量增长中的贡献越来越多,对视频流量的预测则能有效地优化网络任务管理,鉴于多媒体应用对网络流量的增长贡献越来越多,对视频流量的预测能力大小能有效地影响网络任务管理[6, 7, 8]. 视频流量的延迟与遗失敏感特性影响视频传输的实时性,许多诸如IP电话、 游戏、 会议、 远程操作等的网络应用都要求实时或接近实时的内容分发,为实现端到端的网络QoS控制,需要预测具有一定比特率的视频流量时间序列,文[9]中对近20年来关于视频流量,即视频帧大小的不同预测方法进行了回顾和展望. 因此,设计精确的网络流量预测模型[10, 11, 12, 13, 14]有助于实现动态带宽配置、 网络拥塞控制、 资源接入控制等,能有效地提高网络利用率,促进网络管理的优化.
在网络流量预测方面,考虑到流量动态传输中的非线性特性,基于神经网络、 支持向量机(support vector machine,SVM)方法、 自适应信号处理技术的非线性预测方法已经取得了许多成功应用. 例如,文[1]中用基于量子自适应粒子群优化径向基函数神经网络预测网络流量; 文[2]中用局域LSSVM(least square support vector machine)方法预测小尺度网络流量; 文[7]中采用NARX(nonlinear auto-regressive with exogenous variables)神经网络对视频流量时间序列进行预测; 文[15]中用多层前馈神经网络方法预测MPEG(moving picture experts group)视频流量; 文[16]中采用信号处理中的稀疏子集选择在线自适应预测视频流量的I帧、 P帧、 B帧; 文[17]中用递归神经网络方法分别预测MPEG视频流量的I帧、 P帧、 B帧; 它们均取得了较好的预测效果. 但现有文献中的预测方法大都是全局建模方法,网络结构较为复杂,具有一定的应用局限性.
考虑到SOM[18]神经网络具有非监督学习特性的优点,与其它神经网络相比,SOM神经网络还具有对权值初始化取值敏感程度较弱的优点. 通过引入动态嵌入流(dynamic embedding manifold,DEM)将SOM联想记忆技术推广到时域,可应用于非线性动态系统的建模与时间序列预测上,也称为VQTAM[19]技术. 在VQTAM方法的基础上,将SOM神经网络与局部线性AR模型相结合,所构建的预测模型能自适应捕捉非线性动态特性,进一步提高预测的精度. 因此,针对MPEG视频流量预测,本文提出一类基于SOM神经网络的局部AR方法,具体包括具有多个局部线性AR模型的AR-SOM方法,基于前K个获胜神经元建立单一时变局部AR模型的K-SOM方法,以及同时完成数据集的聚类、 多个局部AR模型系数更新的LLM-SOM方法,将它们应用于相应的视频源流量预测实例中,在同等条件下,与现有的SVM方法以及相关文献的研究结果进行比较,以验证所提出方法的有效性.
2 基于SOM神经网络的局部AR方法作为用SOM实现时间序列预测的一种直接与直观的方法,VQTAM本质上是一种矢量量化算法,可以视为基于SOM的联想记忆技术在时间域的推广,在训练数据集的输入与输出之间同时进行矢量量化. 为了达到较小的预测误差则需要较大的拓扑结构,这在某种程度上限制了它的应用. 为了简化网络的拓扑结构,使用较少数目的神经元即可达到较高的预测精度,将SOM的神经元与局部线性AR模型联系起来,则可形成一类基于SOM的局部线性AR方法,以进一步提高SOM神经网络预测的性能.
2.1 VQTAM方法VQTAM方法采用时间延迟作为短期记忆机制,同时完成非线性映射在输入、 输出空间的向量量化.
针对大小为N的时间序列数据{y(t)},构建单步预测模型如下:
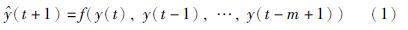
为了逼近式(1)中的非线性映射,输入向量x(t)定义为具有增广形式的两部分,第1部分为模型输入xin(t)=[y(t),y(t-1),…,y(t-m+1)],第2部分为模型输出xout(t)=y(t+1). 神经元的权值向量为wj(t),j=1,…,E,E为神经元数目. wj(t)也相应地分为两部分,因此有:
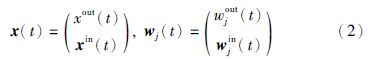
在训练阶段,每个时间步的获胜神经元仅基于xin(t)获得,即:
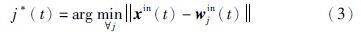
权值更新时,输入向量中的xin(t)与xout(t)两部分均需参与,即:
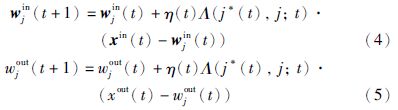
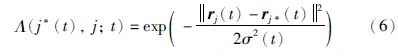
η(t)和σ(t)随时间的增加而逐渐衰减,以保证权值向量收敛,采用指数衰减的形式,如下:
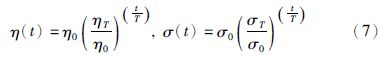
网络训练一旦完成,与xout(t)所对应的权值woutj*(t)即为式(1)的预测输出:
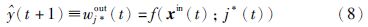
为了改进预测精度,文[20]中给出了一种将局部AR方法与前馈神经网络相结合的策略,取得了很好的预测效果. 同样地,将局部AR方法与VQTAM相结合,利用VQTAM完成有效的线性预测,能够给出对式(1)的更“紧凑”的表示. 一旦VQTAM训练完毕,将训练数据再次输入SOM网络进行聚类,寻找每个数据对应的神经元. 令集合Sj={x1j,x2j,…,xjnj}表示映射到神经元j的包含nj个数据向量的子集(0<nj<<N-m). 其中xij=[xji,0xji,1…xji,m]T表示映射到神经元j的第i个训练数据向量,j=1,…,E.
令AR模型的系数向量aj=[aj,0 aj,1…aj,m]T,利用集合Sj,与神经元j相对应的第j个局部AR模型的系数向量aj用正则化最小二乘法计算如下:
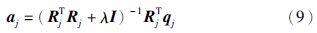

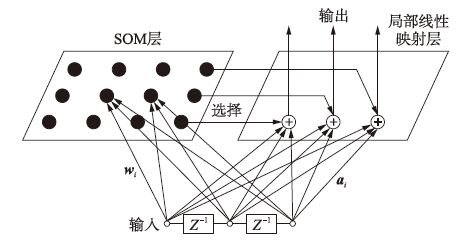
所有j个局部AR模型一旦训练完毕,则系数“冻结”,结构如图 1所示.
|
| 图 1 AR-SOM的动态建模结构 Fig. 1 Structure of AR-SOM for dynamic modeling |
在测试时,给定新的输入向量x+(t),单步预测(t+1)为
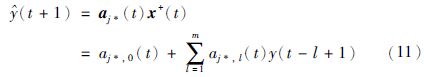
与需要使用E个局部模型的AR-SOM方法不同,K-SOM方法仅需要构建单一的时变线性局部AR模型,选取前K个获胜神经元可降低求逆矩阵的维数. K-SOM方法将标准最小二乘参数估计与VQTAM技术相结合,可以视为一种针对获胜神经元邻域设计的基于VQTAM技术的局部线性插值策略. 针对每个输入向量,K-SOM方法用很少的神经元建立预测器,用非平稳时间序列的局部表示实现预测.
在VQTAM训练完成后,预测时,在每个时间步t选取前K个获胜神经元的权值向量构成一个子集,借助正则化最小二乘法计算单一时变AR模型的系数向量.
每个时间步t,寻找前K个获胜神经元的过程如下:

由K个获胜神经元的权值向量子集{wj*1,wj*2,…,wj*K},可构建局部线性模型如下:
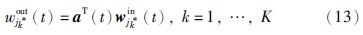
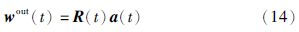
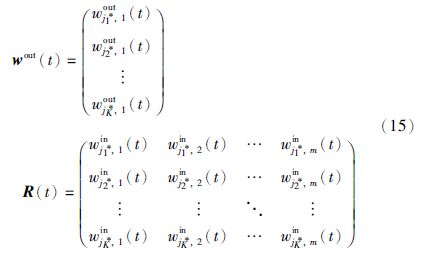
与式(9)的求解类似,基于正则化最小二乘方法更新获胜神经元的系数向量a(t)为
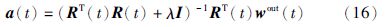
网络的预测输出即为
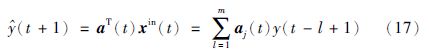
LLM-SOM方法是AR-SOM方法的在线学习模式,可调节参数的数目仍为2mE. 与AR-SOM方法不同,LLM-SOM方法在更新局部模型系数向量的同时完成数据向量的聚类,由于再无需计算矩阵的逆,减少了模型建立过程所需时间和计算负担.
本文方法中,神经元j的权值向量winj(t)的更新规则如式(4)所示. 考虑邻域函数Λ(j*(t),j; t),系数向量aj(t)的训练则按照最小均方(LMS)学习规则在线更新,即:
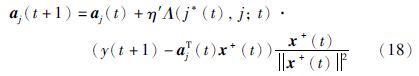
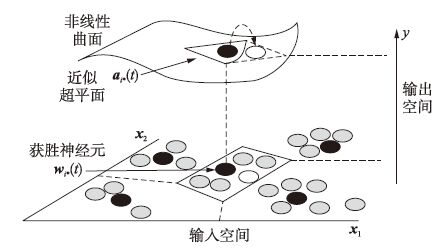
一旦训练完毕,所有系数向量aj(t)“冻结”,供测试数据使用,模型预测输出由目前获胜神经元所对应的局部AR模型计算得出,如式(11)所示. 输入空间被划分为非重叠区域,输入数据子集联系到一个插值超平面,如图 2所示. 本质上看,在训练学习阶段,每个神经元储存输入—输出数据向量的局部梯度信息,在表示输出权向量的输出空间中,梯度信息可给出其一阶扩展形式. 与K-SOM方法相比,LLM-SOM方法采用LMS的学习规则,在更新局部模型系数向量的同时,对数据向量进行聚类. 因此,在线LLM-SOM算法的计算复杂度为O(N).
|
| 图 2 LLM-SOM方法的动态建模结构图 Fig. 2 Structure of LLM-SOM method for dynamic modeling |
针对网络流量预测,在VQTAM的基础上,将具有矢量化特性的VQTAM方法与局部AR模型相结合,提出一类基于SOM神经网络的局部AR方法的算法,实现步骤如下:
1) AR-SOM算法
Step 1 数据预处理及网络初始化. 训练时,若网络流量时间序列的长度为N,构建嵌入维数为m的数据对. 网络的输入向量x(t)=[xout(t),xin(t)]T. 设定网络的拓扑结构大小,网络权值随机初始化,设定学习率η(t)的初值η0与终值ηT,邻域函数有效宽度σ(t)的初值σ0与终值σT.
Step 2 网络训练阶段. 设定网络的迭代次数,将训练数据向量对依次输入. 在时间步t时,获胜神经元j*(t)由式(3)仅依据xin(t)计算获得,但权值向量的更新由式(4)、 式(5)依据网络的输入向量x(t)计算获得.
Step 3 数据分区. 一旦训练阶段完毕,为寻找每个数据向量映射的神经元,将训练数据向量对再次输入给网络. 映射到神经元j的nj个数据构成集合Sj={x1j,x2j,…,xjnj}.
Step 4 AR模型的参数估计. 被映射的每个神经元对应一个局部线性AR模型. 利用集合Sj中的向量,按式(9)计算第j个局部AR模型的系数向量aj.
Step 5 测试阶段. 针对每个测试输入向量,依照式(11)计算其单步预测输出.
2) K-SOM算法
K-SOM无需使用E个局部线性AR模型,仅使用单一的局部线性AR模型,但每个时间步t需更新AR模型的系数向量,其前两个步骤同AR-SOM的算法实现过程,并需设定K的值,经验取值为神经元总数的一半即可.
Step 3 直接进入测试阶段,将测试数据依次输入K-SOM网络,针对每个测试数据向量,按式(12)计算获取前K个获胜神经元.
Step 4 根据式(16)计算系数向量a(t),并计算局部线性AR模型的预测输出.
3) LLM-SOM算法
Step 1 同AR-SOM算法的Step 1.
Step 2 网络的训练为在线方式. 每个时间步t,输入当前数据向量,则由式(3)计算获胜神经元,按式(4)更新权值向量. 与此同时,由式(18)更新每个AR模型的系数向量.
Step 3 训练完毕,针对每个测试数据向量,根据式(11)计算单步预测输出.
3 网络流量预测实验将本文方法应用于网络流量预测实例中,采用信号误差比率(signal-to-error ratio,SRR)[21]、 相对均方误差(relative mean square error,RMSE)作为评价指标,即:
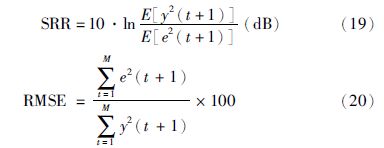
使用的视频迹数据采用MPEG-4压缩标准,MPEG-4图像中的对象是VOP(visual object plane),VOPs与早期版本的MPEG标准中的帧的含义类似,因此,一幅场景中的每个对象可以表示为沿着时间传输的VOPs序列. MPEG-4编码的比特流由帧内编码帧(I帧)、 预测帧(P帧)和双向帧(B帧)组成. 实验数据来源于德国柏林科技大学电信网络组的视频迹序列数据库,其网址为: http://www-tkn.ee.tu-berlin.de/research/trace/trace.html,选取高质量编码的迹时间序列,其平均比特率如表 1所示,反映了迹序列的图像质量信息.
| 迹序列 | 峰值 /均值 | 平均比特率 /(Mbit/s) |
| Die Hard III | 6.6 | 0.2 |
| Jurassic Park I | 4.4 | 0.8 |
| Lecture Room | 11.9 | 0.1 |
针对每个迹序列的I-VOPs、 P-VOPs、 B-VOPs分别进行预测,时间序列均归一化在[-1, 1]之间. 每个迹序列的VOPs总数目为89 998,其中I-VOPs、 P-VOPs、 B-VOPs的数目分别为7 500、 22 500、 59 998. I-VOPs用1 500个数目作为训练数据集,500个数目用于交叉验证,其余部分为测试数据集. P-VOPs中前1 500个数目为训练数据,500个数目用于交叉验证,其余数据组成测试数据集. B-VOPs中训练数据集数目为20 000,用于交叉验证的数据为10 000,其余部分为测试数据. 借助交叉验证的方法可选取较优的网络结构与相应参数.
实验中,应用基于SOM的局部AR方法,初始和最终的学习率取值分别为η0=1,ηT=10-3. 其中,AR-SOM方法选取10×1的神经元网络结构,输入向量的维数m=15,初始的和最终的邻域宽度值分别为σ0=200,σT=0.001. K-SOM方法的神经元结构选取为30×2,实验中,这两种方法对正则化参数λ的选择相对不敏感,建议取值范围为λ∈[0.001,0.005],最好的获胜神经元数目选取为K=25. LLM-SOM方法中,神经元的结构为5×4×3,输入向量的维数m=4,λ=0.001,σ0=n/2,σT=0.001.
为进一步衡量本文方法的有效性,将本文方法的预测结果在相同条件下与BP、 SVM方法构建的预测模型以及相关文献的研究结果均进行比较. 不同方法针对I-VOPs、 P-VOPs、 B-VOPs迹序列的预测结果指标评价分别由表 2、 表 3、 表 4给出. 其中,BP方法的网络结构为15-10-1,采用L-M训练算法. SVM方法采用了标准ε-SVM算法,用高斯核函数k(xi,xj)=exp-0.5xi-xj2/σ2实现,核参数为2,惩罚参数C=10,ε=0.01,用LIBSVM软件完成.
| 迹序列 | BP | SVM | AR-SOM | K-SOM | LLM-SOM | 文[16] | 文[17] | |
| Die Hard III | SRR | 10.081 4 | 16.751 7 | 17.481 1 | 18.501 3 | 18.561 0 | - | - |
| MSE | 0.098 1 | 0.021 1 | 0.017 9 | 0.014 1 | 0.013 9 | 0.018 9 | 0.029 0 | |
| Jurassic Park I | SRR | 6.842 9 | 21.905 4 | 21.621 5 | 22.281 6 | 22.191 8 | - | - |
| RMSE | 0.206 9 | 0.006 4 | 0.006 9 | 0.005 9 | 0.006 0 | 0.007 5 | 0.008 0 | |
| Lecture Room | SRR | 24.027 7 | 33.396 5 | 32.503 7 | 34.784 9 | 34.909 2 | - | - |
| RMSE | 0.004 0 | 4.574 5e-04 | 5.618 7e-04 | 3.322 8e-04 | 3.229 1e-04 | 0.583 0 | 0.002 0 |
| 迹序列 | BP | SVM | AR-SOM | K-SOM | LLM-SOM | 文[16] | 文[17] | |
| Die Hard III | SRR | 5.289 0 | 13.643 2 | 14.440 0 | 14.796 0 | 14.824 8 | - | - |
| RMSE | 0.295 9 | 0.043 2 | 0.036 0 | 0.033 1 | 0.032 9 | 0.041 0 | 0.090 0 | |
| Jurassic Park I | SRR | 14.237 8 | 14.793 1 | 14.672 4 | 14.863 8 | 15.485 0 | - | - |
| RMSE | 0.037 7 | 0.033 2 | 0.034 1 | 0.032 6 | 0.028 3 | 0.033 6 | 0.040 0 | |
| Lecture Room | SRR | 5.731 2 | 19.919 1 | 20.683 2 | 21.119 0 | 21.169 8 | - | - |
| RMSE | 0.267 2 | 0.010 2 | 0.008 5 | 0.007 7 | 0.007 6 | 0.013 6 | 0.069 0 |
| 迹序列 | BP | SVM | AR-SOM | K-SOM | LLM-SOM | 文[16] | 文[17] | |
| Die Hard III | SRR | 0.179 9 | 18.232 2 | 17.869 7 | 18.621 4 | 19.171 0 | - | - |
| RMSE | 0.959 4 | 0.015 0 | 0.016 3 | 0.013 7 | 0.012 1 | 0.015 1 | 0.040 0 | |
| Jurassic Park I | SRR | 2.112 9 | 17.161 7 | 17.379 2 | 17.448 4 | 18.053 8 | - | - |
| RMSE | 0.614 8 | 0.019 2 | 0.018 3 | 0.018 0 | 0.015 7 | 0.017 0 | 0.022 0 | |
| Lecture Room | SRR | 5.372 3 | 22.025 5 | 20.129 5 | 22.153 4 | 21.939 3 | - | - |
| RMSE | 0.290 2 | 0.007 9 | 0.009 7 | 0.006 1 | 0.006 4 | 0.007 2 | 0.283 0 |
表 2~表 4中,与文[16]、 文[17]对比的结果也进一步表明本文方法的有效性. 表 2~表 4中,通过与BP神经网络、 SVM等其它方法进行对比可以看出,一类基于SOM神经网络的局部AR方法取得了较高的预测精度,其中,K-SOM方法和LLM-SOM方法的预测精度更好. 实验结果表明,本文的网络流量预测方法能获得较好的预测效果.
|
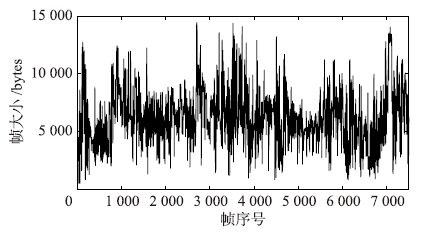
| 图 3 Die Hard III的I-VOPs迹序列 Fig. 3 Actual series for I-VOPs of Die Hard III trace |
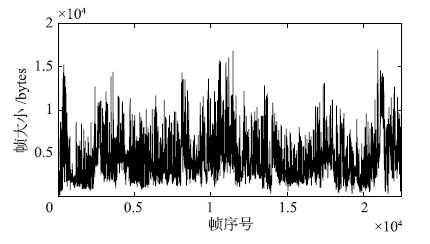
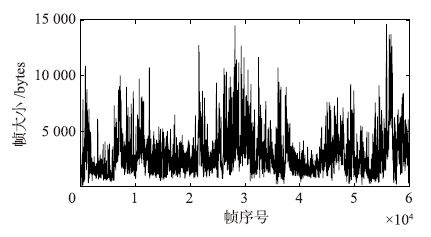
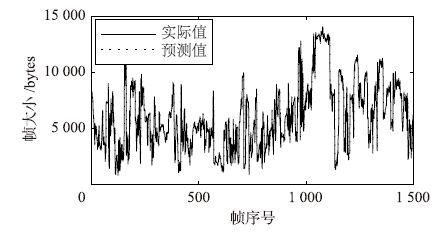
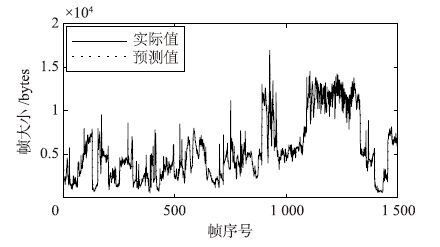
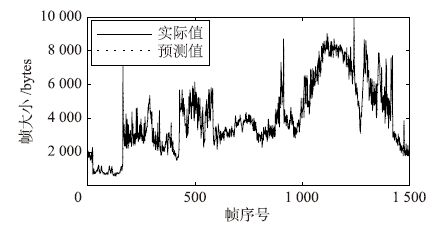
图 3、 图 4、 图 5分别刻画了Die Hard III的视频流量I-VOPs、 P-VOPs与B-VOPs的实际迹序列. 图 6、 图 7、 图 8分别给出了在测试子集上,LLM-SOM方法与实际迹序列在I-VOPs、 P-VOPs与B-VOPs上的预测结果对比图,由图中可以看出,LLM-SOM方法的预测曲线与实际曲线的重合度均较高,取得了满意的预测效果.
|
| 图 4 Die Hard III的P-VOPs迹序列 Fig. 4 Actual series for P-VOPs of Die Hard III trace |
|
| 图 5 Die Hard III的B-VOPs迹序列 Fig. 5 Actual series for B-VOPs of Die Hard III trace |
|
| 图 6 Die Hard III的I-VOPs单步预测结果 Fig. 6 Single-step-ahead predicted result for I-VOPs of Die Hard III |
|
| 图 7 Die Hard III的P-VOPs单步预测结果 Fig. 7 Single-step-ahead predicted result for P-VOPs of Die Hard III |
|
| 图 8 Die Hard III的B-VOPs单步预测结果 Fig. 8 Single-step-ahead predicted result for B-VOPs of Die Hard III |
实验数据选用互联网流量文库(internet traffic archive,ITA)中的贝尔迹(Bellcore traces)数据集[22].
该数据集记录了20世纪80年代末以太网连接下到达贝尔计算实验室的100万个数据包,时间戳为微秒级. 这些迹是寻找以太网流量在长时间内的自相似性与依赖关系的基础. BC-pAug89.TL记录了从1989年8月29日11∶25开始,约3 142.82 s的局域网网络流量数据. BC-pOct89.TL记录了从1989年10月5日11∶00开始,约1 759.62 s的局域网网络流量数据. BC-Oct89Ext.TL记录了从1989年10月3日23∶46开始捕获的100万个外部到达的广域网流量包,约122 797.83 s.
以秒为间隔预处理迹数据,BC-pAug89.TL形成3 143个数据点构成的迹序列,前2 400个用于训练,其余作为测试. BC-pOct89.TL形成1 760个数据点,前1 300个数据点选为训练集,剩余460数据作为测试. BC-Oct89Ext.TL的前15 000个数据点作为训练集,后续5 000个数据点为测试集.
实验中,初始和最终的学习率取值分别为η0=1,ηT=10-3. 序列BC-pAug89.TL的输入向量的维数m=10,BC-pOct89.TL的输入向量的维数m=15,BC-Oct89Ext.TL的输入向量的维数m=4. AR-SOM方法选取10×1的神经元网络结构,λ=0.001,σ0=200,σT=0.001,迭代50次. K-SOM方法的神经元结构为5×4×3,σ0=30,σT=0.000 1. LLM-SOM方法的神经元结构为5×4×3,λ=0.001,σ0=200,σT=0.001.
表 5中,通过与BP神经网络、 SVM等其它方法进行对比可以看出,基于SOM神经网络的局部AR方法应用于网络流量预测中均取得了较高的预测精度,K-SOM方法和LLM-SOM方法的预测精度优于AR-SOM方法.
| 序列 | BP | SVM | AR-SOM | K-SOM | LLM-SOM | |
| BC-pAug89.TL | SRR | 8.493 2 | 8.659 9 | 9.086 2 | 9.125 6 | 9.223 1 |
| RMSE | 0.141 5 | 0.136 1 | 0.123 4 | 0.122 3 | 0.119 6 | |
| BC-pOct89.TL | SRR | 11.199 0 | 13.408 7 | 13.999 2 | 14.101 0 | 14.171 0 |
| RMSE | 0.075 9 | 0.045 6 | 0.039 8 | 0.038 9 | 0.038 3 | |
| BC-Oct89Ext.TL | SRR | 2.910 6 | 4.599 9 | 6.102 4 | 6.431 4 | 6.678 8 |
| RMSE | 0.511 6 | 0.346 7 | 0.245 3 | 0.216 3 | 0.214 8 |
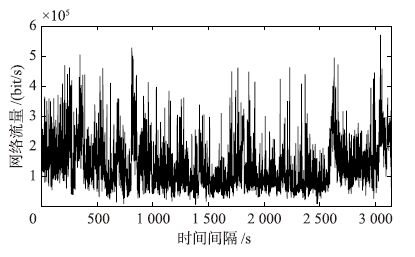
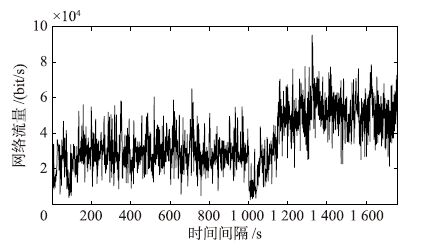
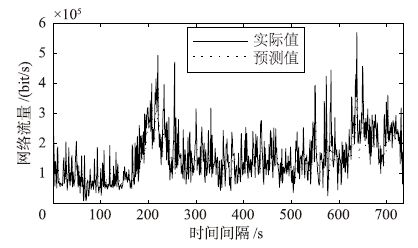
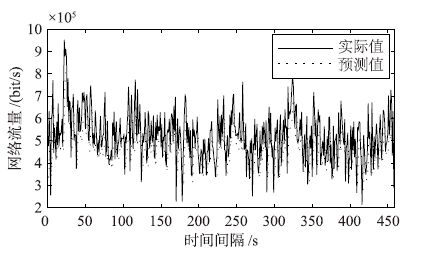
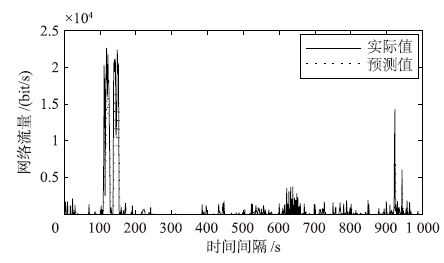
图 9、 图 10、 图 11分别刻画了BC-pAug89.TL、 BC-pOct89.TL和BC-Oct89Ext.TL网络流量序列. 图 12、 图 13、 图 14分别给出了在测试子集上,LLM-SOM方法的预测结果与实际值在3个序列上的对比图,反映了LLM-SOM方法对实际曲线很好的跟随效果,达到了满意的预测精度.
|
| 图 9 BC-pAug89.TL的网络流量迹序列 Fig. 9 Network traffic on BC-pAug89.TL trace |
|
| 图 10 BC-pOct89.TL的网络流量迹序列 Fig. 10 Network traffic on BC-pOct89.TL trace |

|
| 图 11 BC-Oct89Ext.TL的网络流量迹序列 Fig. 11 Network traffic on BC-Oct89Ext.TL trace |
|
| 图 12 BC-pAug89.TL迹序列的单步预测结果 Fig. 12 Single-step-ahead predicted result of BC-pAug89.TL trace |
|
| 图 13 BC-pOct89.TL迹序列的单步预测结果 Fig. 13 Single-step-ahead predicted result of BC-pOct89.TL trace |
|
| 图 14 BC-Oct89Ext.TL迹序列的单步预测结果 Fig. 14 Single-step-ahead predicted result of BC-Oct89Ext.TL trace |
针对网络流量预测,结合SOM的全局拓扑特性和局部AR模型的区域逼近能力,本文给出一类基于SOM神经网络的局部AR方法. 作为不同的局部建模策略,AR-SOM方法及LLM-SOM方法均可逼近输入—输出空间的局部区域,并基于SOM神经网络建立数个局部线性模型. 其中,AR-SOM方法在完成与每个神经元相联系的数据聚类的基础上,同时建立多个局部线性AR模型; K-SOM方法则在每个时间步选择前K个获胜神经元,建立单一的局部AR模型; LLM-SOM方法在更新模型系数向量的同时,完成数据向量的聚类,无需计算矩阵的伪逆,是AR-SOM的在线学习形式. 该类方法利用较少数目的神经元即可完成复杂系统的动态建模任务,降低了计算负担,具有灵活的局部建模结构. 本文方法应用于网络流量预测实例中,在同等条件下与其它现有预测方法对比,结果验证了其有效性.
将来的研究可考虑将具有非线性映射的核学习方法引入到SOM神经网络中,与局部AR模型相结合,以进一步提高网络流量预测的精度. 与此同时,将本文方法延伸至网络流量多步预测中,可以更有效地促进网络资源利用.
| [1] | 郭通, 兰巨龙, 李玉峰, 等. 基于量子自适应粒子群优化径向基函数神经网络的网络流量预测[J]. 电子与信息学报, 2013, 35(9): 2220-2226. Guo T, Lan J L, Li Y F, et al. Network traffic prediction with radial basis function neural network based on quantum adaptive particle swarm optimization[J]. Journal of Electronics & Information Technology, 2013, 35(9): 2220-2226. |
| [2] | 唐舟进, 彭涛, 王文博. 一种基于相关分析的局域最小二乘支持向量机小尺度网络流量预测算法[J]. 物理学报, 2014, 63(13): 130504-1~130504-10. Tang Z J, Peng T, Wang W B. A local least square support vector machine prediction algorithm of small scale network traffic based oncorrelation analysis[J]. Acta Physica Sinica, 2014, 63(13): 130504-1~130504-10. |
| [3] | Qu H, Ma W T, Zhao J H, et al. Prediction method for network traffic based on maximum correntropy criterion[J]. China Communications, 2013, 10(1): 134-145. |
| [4] | Eterovic T, Mrdovic S, Donko D, et al. Data mining meets network analysis: Traffic prediction models[C]//37th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO 2014). Piscataway, NJ, USA: IEEE, 2014: 1479-1484. |
| [5] | 温祥西, 孟相如, 马志强, 等. 小时间尺度网络流量混沌性分析及趋势预测[J]. 电子学报, 2012, 40(8): 1609-1616. Wen X X, Meng X R, Ma Z Q, et al. The chaotic analysis and trend prediction on small-time scale network traffic[J]. Acta Electronica Sinica, 2012, 40(8): 1609-1616. |
| [6] | Wang C H, Chen B S, Lee B K, et al. Long-range prediction for real-time MPEG video traffic: An filter approach[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2008, 18(12): 1771-1775. |
| [7] | Menezes J M P, Barreto G A. Long-term time series prediction with the NARX network: An empirical evaluation[J]. Neurocomputing, 2008, 31(16/17/18): 3335-3343. |
| [8] | Kamisli F. Recursive prediction for joint spatial and temporal prediction in video coding[J]. IEEE Signal Processing Letters, 2014, 21(6): 732-736. |
| [9] | Haddad R J, Mcgarry M P, Seeling P. Video bandwidth forecasting[J]. IEEE Communications Surveys & Tutorials, 2013, 15(4): 1803-1818. |
| [10] | Abdennour A. Evaluation of neural network architectures for MPEG-4 video traffic prediction[J]. IEEE Transactions on Broadcasting, 2006, 52(2): 184-192. |
| [11] | 雷必成, 王万良, 李祖欣. 基于在线LS-SVM 的网络预测控制系统[J]. 信息与控制, 2009, 38(2): 163-169. Lei B C, Wang W L, Li Z X. Networked predictive control system based on online LS-SVM[J]. Information and Control, 2009, 38(2): 163-169. |
| [12] | 陈晓天, 张顺颐, 田婷婷. 基于BP神经网络的IP网络流量预测[J]. 南京邮电大学学报: 自然科学版, 2010, 30(2): 16-21. Chen X T, Zhang S Y, Tian T T. Internet traffic forecasting Based on BP neural network[J]. Journal of Nanjing University of Posts and Telecommunications: Natural Science, 2010, 30(2): 16-21. |
| [13] | 姜明, 吴春明, 张旻, 等. 网络流量预测中的时间序列模型比较研究[J]. 电子学报, 2009(11): 2353-2358. Jiang M, Wu C M, Zhang M, et al. Research on the comparison of time series models for network traffic prediction[J]. Acta Electronica Sinica, 2009(11): 2353-2358. |
| [14] | 李丹丹, 张润彤, 王传臣, 等. 认知网络中基于蚁群算法的网络流量预测模型[J]. 电子学报, 2011, 39(10): 2245-2250. Li D D, Zhang R T, Wang C C, et al. A new network traffic prediction model based on ant colony algorithm in cognitive networks[J]. Acta Electronica Sinica, 2011, 39(10): 2245-2250. |
| [15] | Gavade J D, Kharat P K. Neural network based approach for MPEG video traffic prediction[C]//3rd International Conference on Advances in Recent Technologies in Communication and Computing(ARTCom 2011). Stevenage, UK: IET, 2011: 1-6. |
| [16] | Atiya A F, Aly M A, Parlos A G. Sparse basis selection: New results and application to adaptive prediction of video source traffic[J]. IEEE Transactions on Neural Networks, 2005, 16(5): 1136-1146. |
| [17] | Bhattacharya A, Parlos A G, Atiya A F. Prediction of MPEG-coded video source traffic using recurrent neural networks[J]. IEEE Transactions on Signal Processing, 2003, 51(8): 2177-2190. |
| [18] | Kohonen T. Self-organizing maps[M]. 3rd ed. Berlin, Germany: Springer-Verlag, 2000. |
| [19] | Barreto G A, Araujo A F R. Identification and control of dynamical systems using the self-organizing map[J]. IEEE Transactions on Neural Networks, 2004, 15(5): 1244-1259. |
| [20] | Lehtokangas M, Saarinen J, Kaski K, et al. A network of autoregressive processing units for time series modeling[J]. Applied Mathematics and Computation, 1996, 75(2): 151-165. |
| [21] | Chen B S, Peng S C, Wang K C. Traffic modeling, prediction, and congestion control for high-speed networks: A fuzzy AR approach[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(5): 491-508. |
| [22] | Bellcore lab. Trace available in the internet traffic achieve[EB/OL]. (2008-04-09)[2014-10-21] http://ita.ee.lbl.gov/html/traces.html. |



