1 引言
针对具有未知干扰的线性或非线性系统，对系统的状态进行估计，即进行未知输入观测器设计，近年来得到了国内外专家学者的广泛关注. 在过去几十年中，各种各样的未知输入观测器设计方法已经被提出[1, 2, 3, 4, 5, 6, 7, 8, 9]，并已在故障诊断等领域得到了广泛应用[10, 11, 12]. 然而，上述文献都是在渐近收敛的意义上对系统的状态进行渐近估计. 比较而言，有限时间状态观测器能够在任意短的有限时间内实现对系统状态的估计. 在有限时间观测器的设计中[13, 14, 15, 16, 17]，文[13]基于Luenberger观测器设计思想，针对无未知输入干扰的线性系统，设计了一种有限时间状态估计器. 文[15]给出了一种线性系统有限时间函数观测器设计方法. 文[17]把有限时间观测器设计方法扩展到多输出非线性系统，提出了一种全局有限时间非线性观测器设计方法.
故障诊断技术通常是通过系统输出和观测器输出之间的残差实现故障检测和隔离[18]. 基于未知输入观测器[1, 2, 3, 4, 5, 6, 7, 8, 9]的故障诊断技术[10, 11, 12, 18]，故障诊断的及时性往往受到观测器误差系统的渐近收敛性能的影响，尤其对系统运行初始故障的检测和诊断并不有效. 有限时间状态估计器可以通过设定有限时间参数大小，从而在有限短的时间内实现对系统状态的估计，以保证对初始故障诊断的及时性. 基于此，本文给出了一种基于有限时间观测器的状态估计方法，并通过考虑一种高增益滑模微分器，实现对系统输出微分的有限时间精确估计. 在状态和输出微分的精确估计基础上，给出了一种执行器故障有限时间重构方法.
2 系统描述考虑如下具有执行器故障的不确定系统：
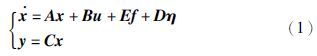
假设1 假设(A，C)是完全可观的且满足下述秩条件：
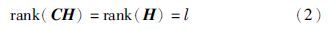
假设2 系统(1)的状态向量、 故障及未知信息及其微分是范数有界的.
本文系统在存在执行器故障及建模不确定性等未知输入的情况下，实现有限时间内的系统状态估计，从而使得在初始运行的短时间内出现的执行器故障得以有效估计或重构.
引理1 给定系统(1)，秩条件(2)成立的条件为：当且仅当存在非奇异变换矩阵U和V使得[2]
UAU-1=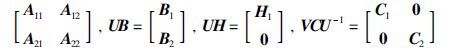
成立，其中A11∈R(q+k)×(q+k)，
A22∈R(n-q-k)×(n-q-k)，
C2∈R(n-q-k)×(n-q-k)和可逆矩阵
C1∈R(q+k)×(q+k)且rank(H1)=q+k.
本节主要实现对原系统(1)的有限时间状态估计. 首先，取状态变换x=Ux和输出变换y=Vy，在假设秩条件1成立的情况下，具有执行器故障的不确定系统(1)能够被转换为下述等价系统：
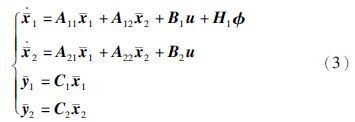
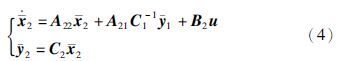
注1 为了在有限时间内，达到对原系统状态估计的目的，需要针对状态和输出变换后的降维系统(4)，在有限时间内对其状态进行估计，并进而利用等价变换得到原系统状态的估计. 因此，基于文[13]构建降维系统(4)的有限时间状态估计器，以达到对其状态进行有限时间估计的目的.
对于降维系统(4)，构造如下2个Luenberger观测器：
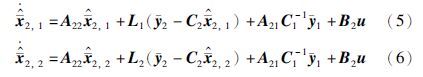
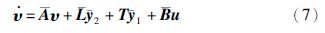
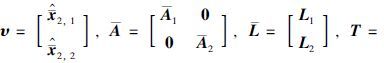
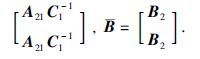
定理1 通过极点配置选择增益矩阵L1和L2，使得A是Hurwitz矩阵，且子矩阵块A1和A2的最大特征值实部满足如下关系：
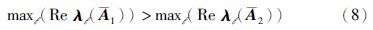
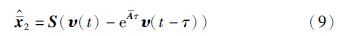
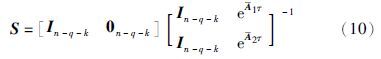
证明 令误差方程为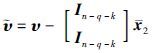
，则可以得到式(4)和式(7)之间的误差系统为
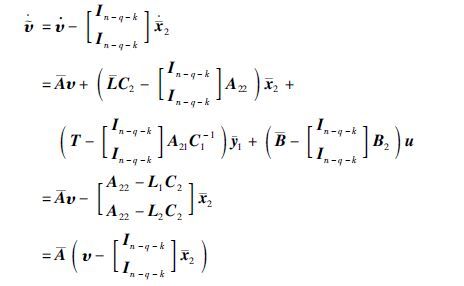
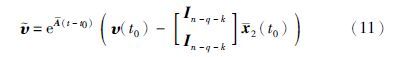
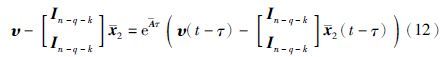
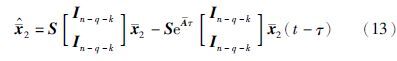
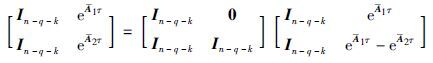
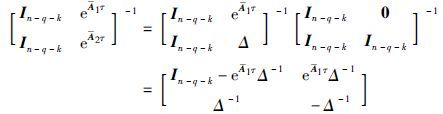
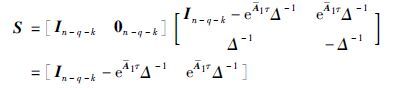
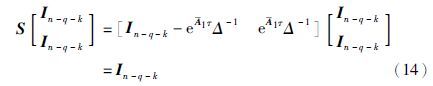
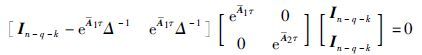
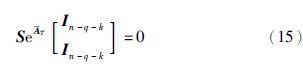
将式(14)和式(15)代入式(13)，可得$\hat{\bar{x}}$2=x2. 故在式(8)成立的情况下，由观测器系统(7)可得具有增益矩阵S的估计状态(9)能够在有限时间τ内估计降维系统(4)的状态.
注2 由于τ是任意正常量，所以理论上其值可设置为无限小，即定理1可以在任意有限小的时间内估计降维系统(4)的状态，这为重构执行器故障提供了基础. 容易通过极点配置求得满足条件(8)的增益矩阵L1和L2. 同时，条件(8)也是增益矩阵S存在的充分条件[12].
注3 对于t∈[0，τ)和初始时刻t0=0，由式(11)得
.
对于t∈［-τ，0]，设υ(t)=υ(t0)=
，结合状态估计式(9)，进一步有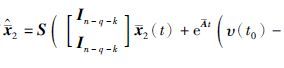
.
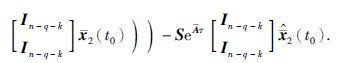将式 (14)和式(15)代入上述状态估计式，可得
$\hat{\bar{x}}$2(t)=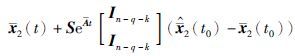
. 其中，t∈[0，τ). 结合式(15)可知，在t=τ时，$\hat{\bar{x}}$2是降维状态$\hat{\bar{x}}$2的精确估计.
在基于定理1得到降维系统(4)的有限时间状态估计之后，基于状态等价变换x=Ux容易得到原系统(1)的状态估计，即可以得到如下推论.
推论 在条件(8)成立的情况下，由式(7)、 式(9)和式(10)组成有限时间观测器，系统(1)的有限时间状态估计为
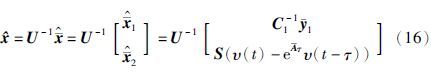
本节通过构造有限时间滑模微分器，对系统输出的微分进行有限时间精确估计，并在此基础上给出执行器故障和建模不确定信息的估计方法.
将系统输出y表示为y=［y1 y2 … yp]T，其中yi=cix(i=1，2，…，p)为系统输出的第i个分量，其中ci是输出矩阵C的第i行向量. 针对系统输出的第i个分量yi，基于假设2并构造如下高增益滑模微分器：
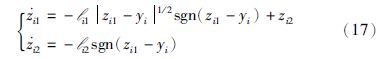
依据文[19]，合理选择微分器的高增益参数li1和li2，则在有限时间内可以使得下述方程组成立：
根据式(17)可知，如果在有限时间内式(18)成立，那么可以得到$\dot y$i=$\dot z$i1=zi2，即zi2在有限时间内是系统输出分量yi微分的精确估计. 从而可以得到向量z=[z12z22…zp2]T是原系统输出向量微分$\dot y$=[$\dot y$1$\dot y$2…$\dot y$p]T的精确估计.
基于高增益滑模微分器得到输出微分的估计之后，下面基于原系统(1)，提出能同时对执行器故障和未知干扰估计的方法. 由系统(1)容易得到$\dot y$=C(Ax+Bu+H$\phi $)，进而根据假设1可以得到：
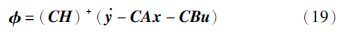
基于推论1和高增益滑模微分器，给出如下用于对原系统的执行器故障和未知输入进行估计方法.
定理2 在假设1和假设2成立的前提下，那么下式估计是执行器故障和未知建模不确定性信息的估计.
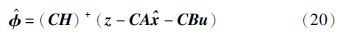
证明 根据式(19)和式(20)容易得到估计误差方程为${\tilde \phi }$=(CH)+(${\tilde z}$-CA${\tilde x}$)，其中${\tilde z}$=z-$\dot y$、 ${\tilde \phi }$=${\hat \phi }$-$\phi $和${\tilde x}$=${\hat x }$-x. 由推论1知z和${\hat x }$分别是输出微分${\dot y}$和状态x的有限时间估计，故${\hat \phi }$是$\phi $的有限时间估计.
在得到未知向量$\phi $的有限时间估计${\hat \phi }$之后，由于$\phi $=[ηT fT]T，可得执行器故障和未知信息的估计为
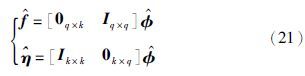
为了验证本文所提方法的有效性，本节考虑对具有执行器故障和未知干扰的F-16飞行器模型进行仿真[20]. 在飞行器参数分别为： 高度H=500 m，发动机油门参数T=0.146 4，总空速Vt=152.4 m/s和参考重心位置参数Xcg=0.35的情况下，假设系统状态参数x=[αwβvχr]T，其中α、 v、 w分别为飞行器沿X、 Y和Z坐标轴方向的速度分量； χ、 β和r分别为飞行器的侧倾角、 俯仰角和偏航角. 系统的已知输入u=[δhr δhl δar δal δr]T，其中δhr、 δhl、 δar、 δal和δr分别为右横向稳定器、 左横向稳定器、 右副翼、 左副翼和方向舵的信号. 系统输出向量为y=[β μrot rstab $\vartheta $ θ]T，其中μrot为稳定轴滚转角，rstab为稳定轴偏航角，$\vartheta $和θ分别为攻击角和侧滑角. 那么形如式(1)的F-16飞行器纵向模型如下：
在仿真中，执行器故障设定为f=2.5cos(2t)，建模不确定性或外部未知干扰为η=1.6sin(2.6t+2.8)，已知输入向量为u=[u1 u2 u3 u4 u5]T，其中u1=sin t、 u2=3cos(2.5t)、 u3=sin(1.8t)、 u4=cos(4.2t+1.8)、 u5=2.8cos(3.2t-9.6).
基于文[2]，可得满足引理1的非奇异变换矩阵U和V，并利用状态变换x=Ux和输出变换y=Vy，那么原系统可转化为分解系统(3)，并进而得到降维解耦系统(4). 对于(A22，C2)和期望特征值组Π=｛-1，-3，-5，-7｝和Π′=｛-10，-13，-15，-17｝，通过极点配置获得满足λl(A22-L1C2)∈Π和λl(A22-L2C2)∈Π′的观测器矩阵L1和L2，即条件(8)得以满足. 进而得到观测器系统(7)中的参数矩阵A、 L、 T、 B. 设有限时间参数τ=0.5，得满足式(10)的状态估计矩阵S. 之后，设置初值υ(0)=[$\hat{\bar{x}}$2，1T(0) $\hat{\bar{x}}$2，2T(0)]T=[x2T(0) x2T(0)]T和x2(0)=[-0.61 0.53 -0.21 -0.87]T，那么根据式(7)、 式(9)和注3，可得如图 1所示的有限时间状态估计误差曲线.
|
| 图 1 τ=0.5时的x2估计误差曲线 Fig. 1 Error curves of x2 when τ=0.5 |
由图 1可知，在系统运行的0.5 s内实现了状态估计. 为了更进一步说明由式(7)和式(9)形成的状态估计器的有限时间估计特性，在初始值不变的情况下，设定有限时间参数τ=0.1，可得到此时的状态估计效果如图 2所示. 由图 1和图 2可知，在改变时间参数的情况下，状态估计器可以在任意小的设定有限时间内实现状态估计.
|
| 图 2 τ=0.1时的x2估计误差曲线 Fig. 2 Error curves of x2 when τ=0.1 |
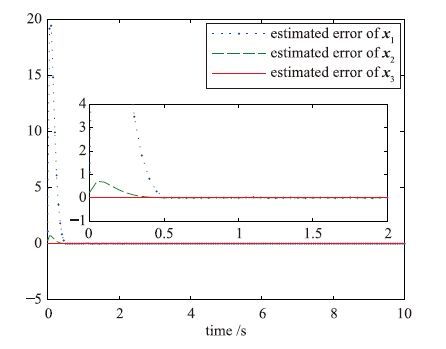
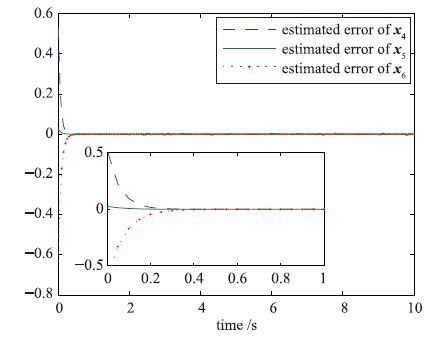
以下仿真是在τ=0.5的情况下进行. 在得到降维系统的状态估计之后，基于推论1中式(16)，可进一步得到原系统的状态估计. 系统状态初值设定为x(0)=[0.8 0.42 -0.65 0.53 0.21 -0.45]T，则可得原系统状态估计误差曲线如图 3和图 4所示，由图可知其有限时间状态估计效果很明显.
|
| 图 3 状态x1~x3估计误差曲线 Fig. 3 Error curves of x1~x3 |
|
| 图 4 状态x4~x6估计误差曲线 Fig. 4 Error curves of x4~x6 |
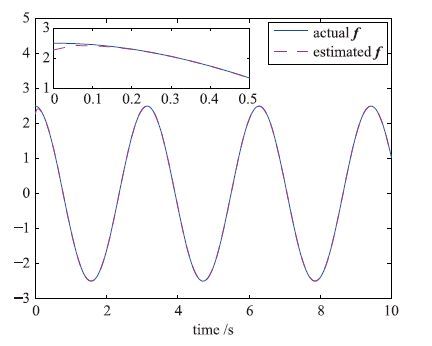
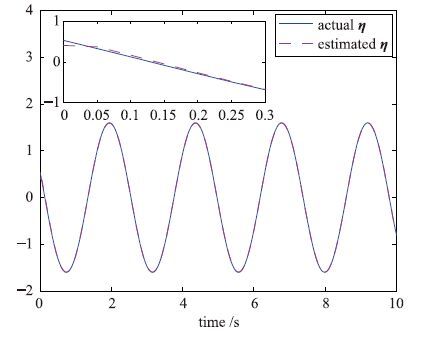
在得到原系统(1)的状态估计之后，为了进一步了解系统的执行器故障信号，这里首先采用高增益滑模微分器(17)，对系统输出信号的微分进行精确估计. 之后，基于输出微分信号的估计和系统的状态估计，利用式(20)和式(21)可以得到原系统执行器故障信号f的估计，同时也可以得到建模不确定等未知信息η的估计，其估计效果如图 5和图 6所示.
|
| 图 5 执行器故障f的重构曲线 Fig. 5 Reconstructed curves of f |
|
| 图 6 未知输入η的重构曲线 Fig. 6 Reconstructed curves of η |
本文基于状态和输出等价变换及有限时间状态估计理论，提出了一种同时对执行器故障与系统建模不确定性信息进行估计的方法. 首先，通过等价变换将具有未知信息和执行器故障的系统转化为降维解耦系统； 其次，通过设计有限时间状态估计器，实现对降维系统状态的估计，并基于状态变换得到原系统状态的有限时间估计； 最后，考虑一种高增益滑模微分器，对系统的输出微分信息进行有限时间精确估计，并在状态和输出微分有限时间估计的基础上，提出一种未知信息重构方法，从而达到对执行器故障重构的目的.
| [1] | Corless M, Tu J. State and input estimation for a class of uncertain systems[J]. Automatica, 1998, 34(6): 757-764. |
| [2] | Hui S, Zak S H. Observer design for systems with unknown inputs[J]. International Journal of Applied Mathematics and Computer Science, 2005, 15(4): 431-446. |
| [3] | Floquet T, Edwards C, Spurgeon S K. On sliding mode observers for systems with unknown inputs[J]. International Journal of Adaptive Control and Signal Processing, 2007, 21(8/9): 638-656. |
| [4] | Shtessel Y B, Baev S, Edwards C, et al. HOSM observer for a class of non-minimum phase causal nonlinear MIMO systems[J]. IEEE Transactions on Automatic Control, 2010, 55(2): 543-548. |
| [5] | Koenig D, Marx B, Jacquet D. Unknown input observers for switched nonlinear discrete time descriptor systems[J]. IEEE Transactions on Automatic Control, 2008, 53(1): 373-379. |
| [6] | Kalsi K, Lian J M, Hui S, et al. Sliding-mode observers for systems with unknown inputs: A high-gain approach[J]. Automatica, 2010, 46(2): 347-353. |
| [7] | Lungu M, Lungu R. Full-order observer design for linear systems with unknown inputs[J]. International Journal of Control, 2012, 85(10): 1602-1615. |
| [8] | Bejarano F J, Pisano A. Switched observers for switched linear systems with unknown inputs[J]. IEEE Transactions on Automatic Control, 2011, 56(3): 681-686. |
| [9] | 杨俊起, 朱芳来. 未知输入和可测噪声重构之线性矩阵不等式非线性系统观测器设计[J]. 控制理论与应用, 2014, 31(4): 538-544. Yang J Q, Zhu F L. Linear-matrix-inequality observer design of nonlinear systems with unknown input and measurement noise reconstruction[J]. Control Theory & Applications, 2014, 31(4): 538-544. |
| [10] | 胡志坤, 孙岩, 姜斌, 等. 一种基于最优未知输入观测器的故障诊断方法[J]. 自动化学报, 2013, 39(8): 1225-1230. Hu Z K, Sun Y, Jiang B, et al. An optimal unknown input observer based fault diagnosis method[J]. Acta Automatica Sinica, 2013, 39(8): 1225-1230. |
| [11] | 陈刚, 林青. 基于观测器的多智能体系统一致性控制与故障检测[J]. 控制理论与应用, 2014, 31(5): 584-591. Chen G, Lin Q. Observer-based consensus control and fault detection for multi-agent systems[J]. Control Theory & Applications, 2014, 31(5): 584-591. |
| [12] | Ríos H, Kamal S, Fridman L M, et al. Fault tolerant control allocation via continuous integral sliding-modes: A HOSM-observer approach[J]. Automatica, 2015, 51: 318-325. |
| [13] | Engel R, Kreisselmeier G. A continuous-time observer which converges in finite time[J]. IEEE Transactions on Automatic Control, 2002, 47(7): 1202-1204. |
| [14] | Raff T, Allgöwer F. An observer that converges in finite time due to measurement-based state updates[C]//Proceedings of the 17th IFAC World Congress. Kington, UK: IFAC, 2008: 2693-2695. |
| [15] | Raff T, Menold P, Ebenbauer C, et al. A finite time functional observer for linear systems[C]//Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference. Piscataway, NJ, USA: IEEE, 2005: 7198-7203. |
| [16] | Ménard T, Moulay E, Perruquetti W. A global high-gain finite-time observer[J]. IEEE Transactions on Automatic Control, 2010, 55(6): 1500-1506. |
| [17] | Shen Y J, Huang Y H, Gu J. Global finite-time observers for Lipschitz nonlinear systems[J]. IEEE Transactions on Automatic Control, 2011, 56(2): 418-424. |
| [18] | 杨俊起, 朱芳来. 基于高增益鲁棒滑模观测器的故障检测和隔离[J]. 自动化学报, 2012, 38(12): 2005-2013. Yang J Q, Zhu F L. FDI based on high-gain robust sliding mode observers[J]. Acta Automatica Sinica, 2012, 38(12): 2005-2013. |
| [19] | Levant A. High-order sliding modes: Differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9/10): 924-941. |
| [20] | Fekih A. Fault-tolerant flight control design for effective and reliable aircraft systems[J]. Journal of Control and Decision, 2014, 1(4): 299-316. |