1 引言
在电力系统的发电产业中，风能作为一种有效的绿色可再生能源，具有广阔的应用前景. 随着风电场的风力发电装机容量不断攀升，风电在电力系统中高度渗透. 由于风能的间歇性和随机性，导致风电功率输出具有强波动性，给电网的稳定性、 安全经济运行以及电能的可靠性方面带来挑战[1, 2, 3]. 因此，风电功率的准确预测对保持电力系统的功率平衡和经济运行具有重要的意义.
风电功率时间序列是受随机因素影响的非平稳性序列，对其变化特性进行先验分析往往有助于提高功率预测的精度. 近年来由文[4]提出的经验模态分解(empirical mode decomposition，EMD)是一种处理非线性和非平稳信号的方法，EMD利用信号自身的极值特性分解出具有不同尺度特性的本征模态分量(intrinsic mode function，IMF)，但在分解过程中易出现模态混叠现象. 集成经验模态分解(ensemble empirical mode decomposition，EEMD)[5]通过添加辅助噪声来消除EMD出现的模态混叠现象，通过多次实验进行平均，抵消和抑制分解结果中噪声所产生的影响. 但在有限次的集成平均后，其重构分量中仍然存在残留的白噪声，虽然可以通过增加集成次数来降低重构误差，但计算规模较大. 具有自适应白噪声的完整集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)[6]方法在分解的每一个阶段都添加自适应的白噪声，然后计算唯一的余量信号获取各个模态分量，解决了EEMD重构误差不为零、 分解效率低等问题，且其分解过程具有完整性. EMD与支持向量机(support vector machine，SVM)结合[7]以及EEMD与动态神经网络结合的组合预测[8]方法已应用于短期电力负荷预测中，同样，EMD与SVM的组合预测方法也已应用于风电功率预测[9]中. 与单一预测方法相比，上述组合预测方法均取得了不错的预测效果.
极限学习机(extreme learning machine，ELM)是2006年Huang等[10]提出的一种性能优良的计算智能方法，其本质是一种单隐层前馈神经网络. 该方法无需通过多次迭代调整神经网络权值，不仅极大地提高了学习速度和泛化能力，而且避免了梯度下降法神经网络易陷入局部极小的风险. 结合核学习方法，文[10]给出一种核极限学习机方法，取得不错的学习性能.
考虑到组合预测方法在短期风电功率预测方面的优势，本文提出一种基于CEEMDAN-模糊熵(fuzzy entropy，FE)-KELM的组合预测方法. 首先利用CEEMDAN方法将风电功率时间序列分解为一系列IMF分量； 其次，利用模糊熵[11, 12]对各IMF分量进行复杂度分析，根据熵值的不同将各IMF进行重组； 然后对重组后的子序列分别构建基于KELM的预测模型； 最后将各子序列的预测结果进行合成. 将本文方法应用于某地区的风电功率预测实例中，并与单一的KELM方法及CEEMDAN-FE-ELM方法进行比较以验证本文方法的有效性.
2 CEEMDAN-FE-KELM方法 2.1 CEEMDAN方法EMD方法是一种非平稳信号的处理方法，类似于小波分析，但克服了小波函数主观选择对信号处理的影响[13]，其本质是将复杂的非平稳信号按波动尺度依次分离出不同的IMF分量. 在EMD方法的基础上，EEMD方法通过多次向原信号添加不同的白噪声，并分别进行EMD分解，然后对多次EMD分解的IMF进行集成平均而得到最终的实际分量. 这能有效地改善EMD方法所存在的模态混叠现象，而且也起到抵消白噪声影响的作用. 随着集成平均次数的增加，EEMD方法虽然可以降低重构误差，但很大程度上增加了计算耗时.
CEEMDAN方法通过在每个阶段添加有限次的自适应白噪声，克服了EEMD方法在较少的实验平均次数下重构误差较大的缺点.
令s(n)表示原始信号序列，νi(n)代表第i次实验中
添加的具有标准正态分布的白噪声序列，则第i次的信号序列表示为si(n)=s(n)+ε0νi(n)(i=1，…，I)，其中I表示实验次数. 首先定义算子Ek(·)为应用EMD方法所产生的第k个阶段的模态分量，CEEMDAN方法产生第k个模态分量记为$\widetilde {IM{F_k}}$，其算法的实现步骤如下：
(1) 与EEMD分解方法相同，针对信号s(n)=ε0νi(n)进行I次实验，通过EMD方法分解以获取第1个模态分量，即：
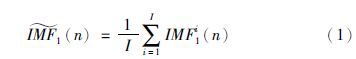
(2) 在第1阶段(k=1)，计算第一个唯一的余量信号，即计算r1(n)=s(n)-$\widetilde {IM{F_1}}$(n).
(3) 进行i次实验(i=1，…，I)，每次实验中，对信号r1(n)+ε1E1(νi(n))进行分解，直至得到第1个模态分量为止. 在此基础上，计算第2个模态分量如下：
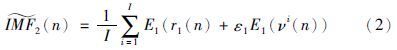
(4) 对其余每个阶段，即k=2，…，K，与步骤3的计算过程一致，首先计算第k个余量信号，再计算第k+1个模态分量，即有：
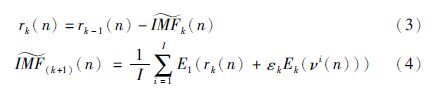
(5) 重复执行步骤4，直至所获取的余量信号不再可能进行分解时为止. 算法终止的准则为余量信号的极值点个数至多不超过2个.
算法终止时，若所有模态分量的数量为K，则最终的余量信号为
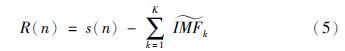
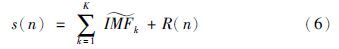
算法实现中，每次实验中的系数εk能够允许在每一个模态分解阶段选择合适的信噪比(SNR).
从CEEMDAN的算法实现及式(6)可知，CEEMDAN的分解过程是完整的，能对原始信号进行精确重构. 因此，CEEMDAN方法可以克服EMD方法存在的模态混叠现象. 同时，与EEMD分解的不完整性及依靠增大集成次数来降低重构误差的不足相比，CEEMDAN方法有显著改进.
2.2 模糊熵作为样本熵与近似熵方法的改进，模糊熵(FE)也是一种衡量时间序列复杂度的测度方法，它被成功应用于表面肌电信号的特征提取. FE是条件概率的负自然对数，它描述由m个点构成的向量与紧邻的由m+1个点构成的向量之间的相似性. 基于模糊集的概念，利用指数函数对向量的相似性进行模糊化定义来获取熵值. 除了具有样本熵、 近似熵的优点之外，FE还能在参数值很小的情况下给出熵的定义，能够随参数的调整稳定变化.
FE的定义过程如下：
(1) 对N个采样点的时间序列｛s(n)，n=1，2，…，N｝进行相空间重构，得到m维的重构向量：
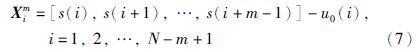
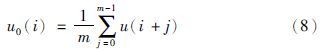
(2) 距离d[Xim，Xjm]表示Xim与Xjm对应元素值之间差异的最大绝对值，即：
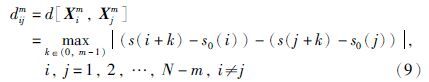
(3) 通过具有指数形式的模糊函数μ(dmij，n，r)，给定参数n和r，计算Xim和Xjm的相似度Dmij，即：
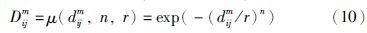
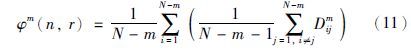
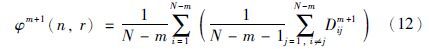
(4) 利用负自然对数，模糊熵可定义如下
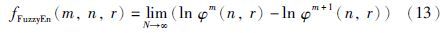
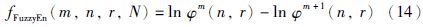
计算模糊熵fFuzzyEn时，m越大则所需要的时间序列长度N就越大(N=10m～30m)，依据文[11]，一般嵌入维数m取2或3即可. r表示模糊函数边界的宽度，取值过大会丢失很多统计信息，取0.1～0.25σSD即可，σSD是原始序列的标准差. n计算时取整数2或3即可.
2.3 KELM方法ELM方法是一种单隐层前馈神经网络，其网络结构由隐含层节点数随机确定，网络输入权值及隐含层节点参数也是随机给定. 训练时仅需考虑调节网络的输出权值，从而极快地提高网络训练速度.
2.3.1 ELM方法对于含有L个隐层节点的SLFNs，给定N组训练样本数据集(xj，tj)∈Rn×Rm，即xj=[xj1，xj2，…，xjn]T，tj=[tj1，tj2，…，tjm]T，则其网络节点的输出为
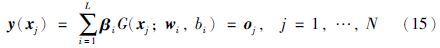
若SLFNs能以零误差逼近训练样本，即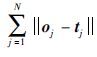
=0，则存在βi、 wi、 bi，使：
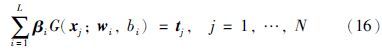
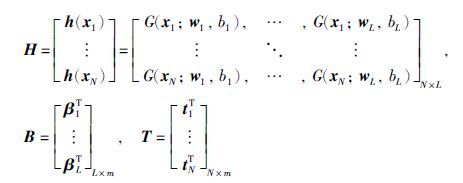
如果激活函数G(xj； wi，bi)在任意区间上无限可微，且SLFNs隐含层节点及节点参数可以随机产生，则从插值的思想看，隐含层节点的最大数目L应小于训练样本数目N，事实上，当L=N时，训练误差将为零. 当L ＜N时，由文[14]可知，SLFNs可以极小的训练误差逼近训练样本，此时矩阵H并非方阵，从而存在${\hat \beta }$i、 ${\hat w }$i、 ${\hat b }$i，使得
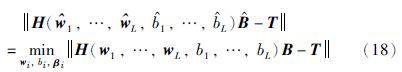
由式(18)可知，与使用梯度下降算法训练所有网络权值不同，ELM的训练相当于求解线性方程组HB=T的最小二乘解B，即：
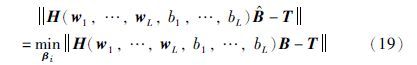
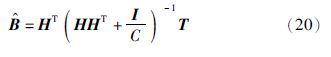
考虑特征映射函数h(x)未知的情形，此时需要将核函数引入到ELM方法中，在式(20)网络输出权值求解的基础上，可形成新的基于核的ELM[15](KELM)方法.
KELM方法中，需定义核矩阵ΩELM=HHT，其元素为ΩELM(i，j)=h(xi)·h(xj)=K(xi，xj). 那么借助式(20)，网络输出可表示为
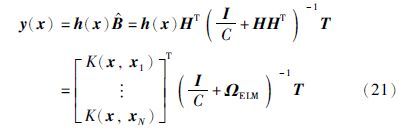
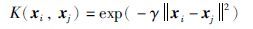
考虑到小波函数具有小波信号局部分析和多分辨分析的优点，而常规函数不具备这样的好处； 其次，小波核函数是正交或近似正交的，而常规核函数是相关甚至是冗余的. 因此，还可选择一种可允许的多维张量积小波核函数[16]：
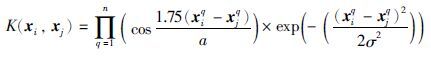
将CEEMDAN-FE-KELM方法应用于某地区的短期风电功率预测实例中.
误差评价指标[17]采用平均绝对百分误差(mean absolute percentage error，MAPE)、 最大误差(maximal error，ME)和均方根误差(root mean square error，RMSE).
总体的组合预测流程如图 1所示.
|
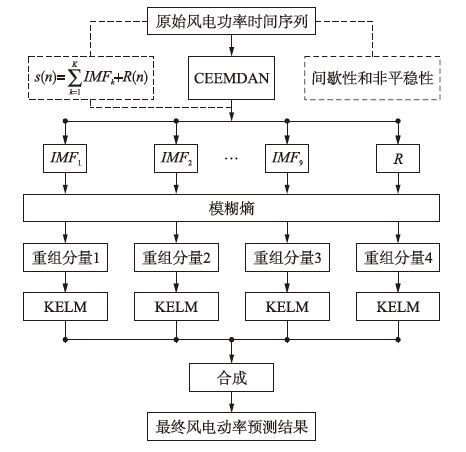
| 图 1 基于CEEMDAN-FE-KELM的组合预测流程图 Fig. 1 Combined forecasting flowchart based on CEEMDAN-FE-KELM |
本节实验采用实际的风场数据，取自于国家可再生能源实验室(NREL)的西部风资源数据集[18, 19]，风电功率的采样间隔为10 min，随机选取连续7天的风电功率数据构成时间序列，80％的数据用于训练，剩余20％的数据用于测试. 按照时间序列建模方式，考虑将历史的风电功率值作为预测输入. 预测模型采用提前6步，即提前1 h的直接多步预测，如下：
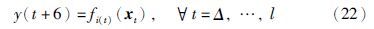
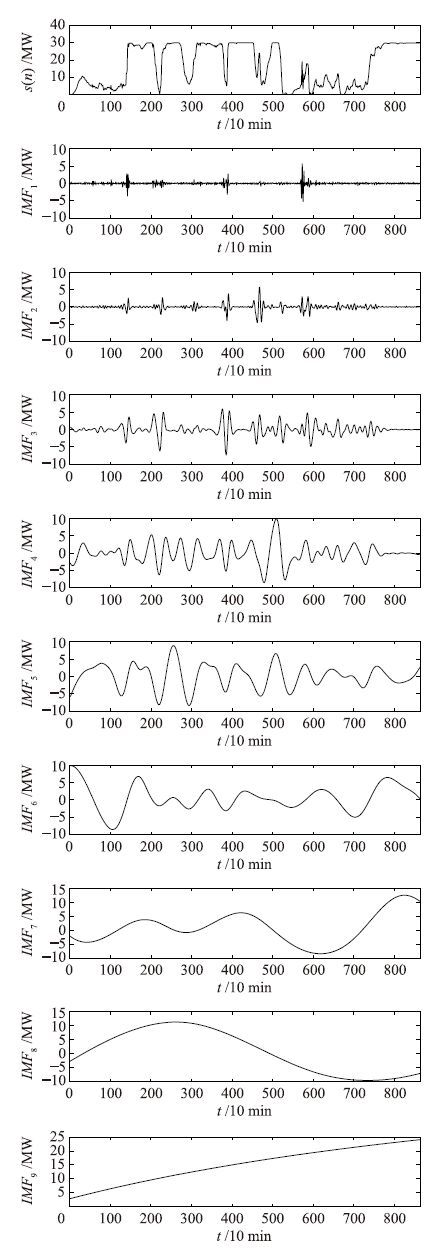
实验中，采用EEMD方法和CEEMDAN方法预先分别对原始的风电功率间序列进行分解，加入I=200组的白噪声信号，其标准差为0.2，分解结果分别如图 2和图 3所示.
|
| 图 2 EEMD方法的分解结果 Fig. 2 The results of EEMD method decomposition |
|
| 图 3 CEEMDAN方法的分解结果 Fig. 3 The results of CEEMDAN method decomposition |
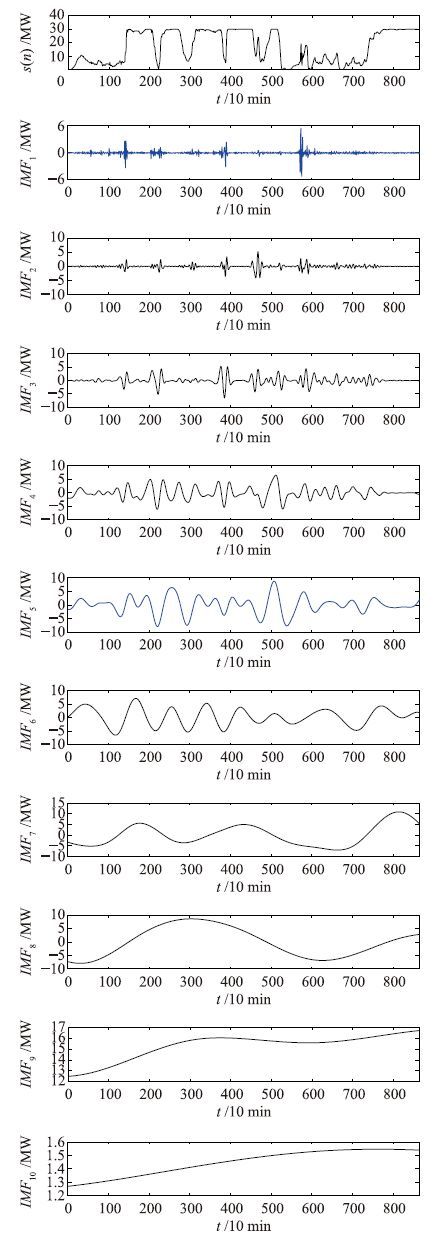
两种分解方法的重构误差由图 4给出，由图 4可知，与EEMD分解方法相比，CEEMDAN分解方法的重构误差明显较小，显然，EEMD分解方法的重构误差显然受到集成次数大小的影响.
|
| 图 4 基于不同分解方法的重构误差 Fig. 4 Reconstruction errors for different decomposition methods |
由于序列的非平稳性使得采用CEEMDAN方法分解后的IMF分量较多，为进一步减小组合预测方法的计算规模，利用FE方法计算各IMF分量的模糊熵值，在此基础上进行合并与重组. 实验中嵌入维数m取2，r=0.2σSD，n=2，计算所得的FE值能较好地展现风电功率时间序列的变化，结果如图 5所示. 由图 5可知，IMF1分量的熵值最大且明显有别于其它分量； IMF2分量和IMF3分量也呈现出较强的随机性，分量IMF4～IMF9和余项分量R的熵值差异较小，将熵值相差不大的相邻IMF分量进行合并，如表 1所示. 经CEEMDAN-FE方法处理后的重组分量，即新的子序列波形如图 6所示.
|
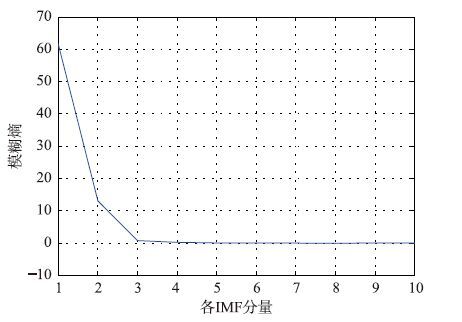
| 图 5 每个IMF分量的模糊熵 Fig. 5 Fuzzy entropy of each IMF component |
| 子序列1 | 子序列2 | 子序列3 | 子序列4 |
| IMF1 | IMF2 | IMF3 | IMF4+…+IMF9+R |
|
| 图 6 经CEEMDAN-FE方法处理后的重组分量 Fig. 6 Recombination components processed by CEEMDAN-FE method |
与文[20]的思路一致，对重组分量的特性进行进一步的分析，分析结果如表 2所示. 由表 2可知，其中重组分量1仅包含一个分量，可以看作高频分量，周期大约为半小时，因此取预测模型的嵌入维Δ=3. 重组分量2的规律性很好，反映了风电功率以一个小时为单位的波动情况，因此可取Δ=6. 重组分量3及重组分量4的整体波动均趋于平缓，可以看作趋势分量，也可取Δ=6.
| 重组分量 | T /10 min | A /MW | 方差 |
| 子序列1 | 3.119 1 | 0.247 0 | 0.259 4 |
| 子序列2 | 6.75 | 0.435 8 | 0.507 2 |
| 子序列3 | 15.428 6 | 1.142 1 | 1.907 3 |
| 子序列4 | 36 | 17.788 5 | 131.682 8 |
在此基础上，对重组后的新子序列分别建立不同的KELM预测模型，对重组分量1和2，考虑选取小波核函数； 对重组分量3和4，考虑选取RBF核函数. 实验中，正则化系数C及核参数可通过交叉验证的方法获取，以获得较优的实验结果.
实验中，对比EMD-KELM方法和EEMD-KELM方法等组合预测方法及单一的KELM预测模型，最终的预测结果如图 7所示. 由图 7可知，CEEMDAN-FE-KELM方法的组合预测效果很好. 不同预测方法的MAPE、 ME和RMSE性能指标如表 3所示. 由表 3可知，CEEMDAN-FE-KELM组合预测方法预测精度最好.
|
| 图 7 风电功率实际值及各模型的提前1 h预测值 Fig. 7 Actual values of wind power and prediction results ahead 1 hour of each prediction model |
| 预测方法 | MAPE | RMSE | ME |
| KELM | 2.536 2 | 0.445 8 | 2.088 1 |
| EMD-KELM | 2.017 8 | 0.327 4 | 1.200 1 |
| EEMD-KELM | 1.014 5 | 0.167 3 | 0.555 3 |
| CEEMDAN-KELM | 0.994 0 | 0.154 0 | 0.639 1 |
| CEEMDAN-FE-KELM | 0.951 7 | 0.145 1 | 0.404 9 |
本文提出了一种基于CEEMDAN-FE-KELM的风电功率组合预测方法. 针对风电功率序列的间歇性和非平稳性，利用CEEMDAN方法将原始的风电功率时间序列进行预处理，将其分解为一系列不同尺度的模态分量. 利用FE方法计算各个IMF分量的模糊熵，按熵值的差异对IMF进行合并与重组. 对重组后的各分量分别建立不同的KELM预测模型，最终对预测结果进行合成. 通过某地区的短期风电功率预测实例进行验证，结果表明，本文方法能获得较好的预测效果，它是EMD方法和ELM方法结合的组合预测方法的延伸，具有很好的工程实用价值，为短期和超短期风电功率预测研究提供了一种新的途径.
| [1] | 谷兴凯, 范高锋, 戴慧珠, 等. 风电功率预测技术综述[J]. 电网技术, 2007, 31(2): 335-338. Gu X K, Fan G F, Dai H Z, et al. Summarization of wind power prediction technology[J]. Power System Technology, 2007, 31(2): 335-338. |
| [2] | 杨秀媛, 肖洋, 陈树勇. 风电场风速和发电功率预测研究[J]. 中国电机工程学报, 2005, 25(11): 1-5. Yang X Y, Xiao Y, Chen S Y. Wind speed and generated power forecasting in wind farm[J]. Proceedings of the CSEE, 2005, 25(11): 1-5. |
| [3] | Wang X, Guo P, Huang X B. A review of wind power forecasting models[J]. Energy Procedia, 2011, 12: 770-778. |
| [4] | Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A - Mathematical Physical and Engineering Sciences, 1998, 454(1971): 903-995. |
| [5] | Wu Z H, Huang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. |
| [6] | Torres M E, Colominas M A, Schlotthauer G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ, USA: IEEE, 2011: 4144-4147. |
| [7] | 祝志慧, 孙云莲, 季宇. 基于EMD和SVM的短期负荷预测[J]. 高电压技术, 2007, 33(5): 118-122. Zhu Z H, Sun Y L, Ji Y. Short-term load forecasting based on EMD and SVM[J]. High Voltage Engineering, 2007, 33(5): 118-122. |
| [8] | 刘岱, 庞松岭, 骆伟. 基于EEMD与动态神经网络的短期负荷预测[J]. 东北电力大学学报: 自然科学版, 2009, 29(6): 20-26. Liu D, Pang S L, Luo W. Power system short-term load forecasting based on EEMD and dynamic neural network[J]. Journal of Northeast DianLi University: Natural Science Edition, 2009, 29(6): 20-26. |
| [9] | 叶林, 刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报, 2011, 31(31): 102-108. Ye L, Liu P. Combined model based on EMD-SVM for short-term wind power prediction[J]. Proceedings of the CSEE, 2011, 31(31): 102-108. |
| [10] | Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/2/3): 489-501. |
| [11] | Chen W T, Wang Z Z, Xie H B, et al. Characterization of surface EMG signal based on fuzzy entropy[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2007, 15(2): 267-272. |
| [12] | 刘慧, 谢洪波, 和卫星, 等. 基于模糊熵的脑电睡眠分期特征提取与分类[J]. 数据采集与处理, 2010, 25(4): 484-489. Liu H, Xie H B, He W X, et al. Characterization and classification of EEG sleep stage based on fuzzy entropy[J]. Journal of Data Acquisition & Processing, 2010, 25(4): 484-489. |
| [13] | 王丽婕, 冬雷, 廖晓钟, 等. 基于小波分析的风电场短期发电功率预测[J]. 中国电机工程学报, 2009, 29(28): 30-33. Wang L J, Dong L, Liao X Z, et al. Short-term power prediction of a wind farm based on wavelet analysis[J]. Proceedings of the CSEE, 2009, 29(28): 30-33. |
| [14] | Liang N Y, Huang G B. A fast and accurate online sequential learning algorithm for feedforward networks[J]. IEEE Transactions on Neural Networks, 2006, 17(6): 1411-1423. |
| [15] | Huang G B, Zhou H M, Ding X J, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42(2): 513-529. |
| [16] | 李军, 郭林. 基于WKGV-KICA的盲源信号分离算法[J]. 控制与决策, 2013, 28(7): 972-977. Li J, Guo L. Blind source separation algorithm based on WKGV-KICA algorithm[J]. Control and Decision, 2013, 28(7): 972-977. |
| [17] | 徐曼, 乔颖, 鲁总相. 短期风电功率预测误差综合评价放法[J]. 电力系统自动化, 2011, 35(12): 20-26. Xu M, Qiao Y, Lu Z X. A comprehensive error evaluation method for short-term wind power prediction[J]. Automation of Electric Power Systems, 2011, 35(12): 20-26. |
| [18] | Lew D, Milligan M, Jordan G, et al. How do wind and solar power affect grid operations: The western wind and solar integration study[C]//8th International Workshop on Large Scale Integration of Wind Power and on Transmission Networks for Offshore Wind Farms. Berlin, Germany: Springer, 2009: 14-15. |
| [19] | Potter C W, Lew D, McCaa J, et al. Creating the dataset for the western wind and solar integration study (U. S. A)[J]. Wind Engineering, 2008, 32(4): 325-338. |
| [20] | 牛东晓, 李媛媛, 乞建勋, 等. 基于经验模式分解与因素影响的负荷分析方法[J]. 中国电机工程学报, 2008, 28(16): 96-102. Niu D X, Li Y Y, Qi J X, et al. A novel approach for load analysis based on empirical mode decomposition and influencing factors[J]. Proceedings of the CSEE, 2008, 28(16): 96-102. |