1 引言
遗传算法(genetic algorithm,GA)由Holland教授于1975年首次提出[1]. 由于遗传算法具有搜索快速、 随机性强、 过程简单、 可扩展性强等优点[2],使其在函数优化、 组合优化等领域中得到了广泛的应用[3, 4, 5].
众所周知,遗传算法在实际应用中存在易早熟、 局部搜索能力差等问题. 为此,很多研究者提出对遗传算法进行改进,以增强其寻优能力. 概况说来,改进工作主要分为两类,一类是各种遗传算法的变形,如模拟退火遗传算法、 小生境遗传算法、 免疫遗传算法等,虽然近年来相关研究取得了很多进展[6, 7],对解决不同类型的优化问题有一定意义,但由于不同方法之间相对独立,其改进工作通常只能在各自领域展开. 另一类工作则是对遗传算法的遗传算子进行改进,以提高遗传算法的自适应能力. 这类改进适用范围广、 通用性强,所以对遗传算子自适应变化的研究仍有较大的意义.
文[8]于1994年最早提出自适应遗传算法,之后又有许多学者进行相关研究. 如文[9]通过Logistic曲线确定遗传算子变化规则,但这种方法受限于曲线自身的变化趋势,与整个进程中种群的变化情况联系不够紧密; 文[10]利用迭代次数提出了交叉变异概率自适应调整方法,但用迭代次数代表种群成熟程度不够精确且无法处理一些不确定终止代数的问题. 目前应用最为广泛的是文[8]与文[11]使用的自适应变化规则,二者均以个体适应度值作为评价指标来确定交叉变异概率的大小. 但通过仿真可以发现,两种方法中遗传算子的变化趋势正好相反,对于提高遗传算法的自适应能力的作用并不确定. 虽然目前也有学者分析过这一现象,但实质性的改进工作仍显不足. 因此,深入研究交叉变异概率的改进方法仍具有理论和实际意义.
进一步分析发现,文[8]与文[11]所提出的以个体适应度值确定遗传算子大小的方法能够保证遗传操作的“优胜劣汰”,有明确的物理意义; 但另一方面,两种方法的不足之处是忽略了种群的变化对遗传操作的影响. 适应度值相同的个体,是否应该更积极地参与交叉变异操作,也是会随着种群的变化而变化的,即“优胜劣汰”的机制也会变化. 鉴于此,本文基于实数编码,根据对种群多样性与相邻代种群间相似性的判定,提出了“种群活力”的概念,同时以种群适应度众数重新定义的种群适应度参考量,设计了一种新的交叉变异概率确定方法. 为了进一步提高算法性能,本文还对变异操作进行了改进,提出并行变异的方法. 仿真结果表明,这种并行变异自适应遗传算法(adaptive genetic algorithm with parallel mutation,AGAP)加快了算法的收敛速度且可进一步避免算法陷入局部收敛,提高了算法性能. 最后,为了验证AGAP算法在实际工程中的应用效果,本文还有针对性地选取了一个一般遗传算法较难解决的多维多约束的工业问题——汽油调和优化调度问题——进行利润寻优仿真,其较好的寻优结果验证了该算法的有效性与实用性.
2 问题分析交叉操作是遗传算法中产生较优个体的主要途径. 假设简单遗传算法使用轮盘赌选择法,且个体适应度值均为正值,则对任意一个大小为H的个体(以下称基因H),其在t时刻被选择的概率为
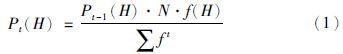
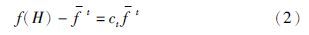
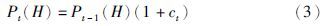
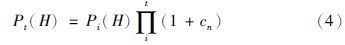
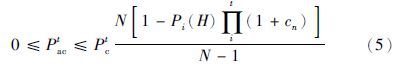
在不考虑变异操作的情况下,由式(5)可以看出,交叉操作产生新个体的概率主要与3个变量有关,即Pct、 Pi(H)和cn. 其中,Pi(H)是随机不可控量,Pct为人工设定值,cn与基因H的适应度值相对大小有关,也是不可控量. 假定大小为H的个体为较优个体,且对任何在一定范围内的整数t,均有f(H)-ft,即ct≥0,则Pact的上限值随着t的增加近似成指数减小,交叉操作将会“失灵”. 实际上这种现象在进化后期尤为明显,如果f(H)不是全局最优适应度值,则很难产生更优个体,算法很容易陷入局部收敛.
因此,可以得到以下3个结论:
结论1 进化前期,新个体主要由交叉操作产生,可设置较大的交叉概率,较小的变异概率. 进化后期几乎不能通过交叉操作得到新个体,交叉概率可以为较小值.
结论2 进化后期,变异操作对新个体的产生有更大的影响,可以适当增加变异概率并对变异操作加以改进,以防陷入局部最优解.
结论3 由于新个体的产生与个体适应度值的相对大小有关,同时结论1、 2都需要对进化进程有较为准确的评判,因此遗传算子的设定应综合考虑个体适应度值与进化进程的影响.
根据以上结论,本文定义“种群活力”作为评价算法进程的指标,提出一种新的参数自适应调整方法,同时引入并行变异操作,以提高算法性能.
3 种群活力评价指标一般情况下,遗传算法进行到后期往往会出现两种情况,即种群多样性降低及相邻代种群之间相似度变大. 根据这两个特点,本文分别设计了新的种群多样性和相邻代种群相似度的判定方法,并综合二者,提出了一种新的种群质量评价指标.
如文[12]等,许多研究均以种群多样性作为种群质量的评价指标,然而这些方法往往在变量取值范围较大时,有时会出现计算量过大或者衡量效果不明显等问题. 对此,本文综合利用个体适应度平均值、 最小值、 最大值与种群个体分布情况,设计了一种新的种群多样性度量函数α(t):
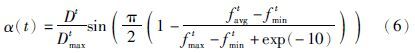
式(6)用种群适应值的分布情况作为多样性的评判依据,并利用正弦函数在[0,π/2]区间的曲线分布进行修正,以避免出现多样性值跳变或变化范围过小的问题. 同时,引入方差修正项来兼顾整个种群的离散程度,从而对种群的描述更加准确.
另外,如果新个体产生不足,则会使新产生的种群与原种群极为相似,即相邻代种群间相似度较高,此时就需要改变交叉变异概率,进而产生差异性更大的种群. 本文利用“余弦相似性”的相关理论,对相邻代种群间相似度进行定义. 定义第t代与第t-1代种群间的相似度β(t)为
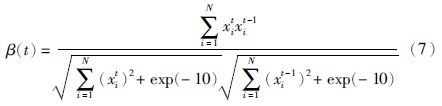
为了验证本文提出的多样性函数与相邻代种群相似度的有效性,取函数:
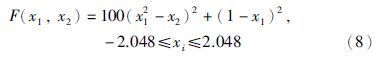
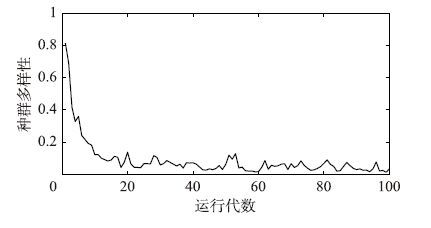
|
| 图 1 种群多样性 Fig. 1 Diversity of population |
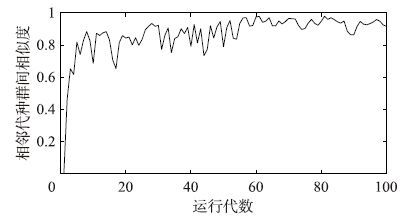
|
| 图 2 相邻代种群间相似度 Fig. 2 Similarity between adjacent populations |
由图 1、 2可见,随着进化代数的增加,种群多样性变化趋势为逐渐降低,α(t)逐渐由1趋于0,而相邻代种群间相似度逐渐升高,β(t)由0逐渐接近1,从而证明了本文针对二者提出的评价指标的有效性.
鉴于α(t)与β(t)分别能独立地从不同角度反映出进化中的种群质量,本文将二者在同一标准下结合起来,提出一种新的种群质量评价指标——种群活力θ:
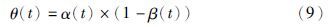
显然,θ(t)越接近1,表示种群活力越高; 反之,越接近0,则表示种群活力越低,而该指标将作为下文中遗传算子自适应调整的重要参考依据.
4 改进的遗传算法 4.1 种群适应度参考量的选取目前有关自适应遗传算法的研究中,大多是以种群平均适应度作为判断个体适应度值相对大小的参考量. 然而此类方法并没有充分考虑遗传算法固有的两个特点: 即选择重复性与交叉变异不定向性. 选择重复性是指遗传算法的选择操作会使某些优良个体在产生的新一代种群中出现的频数较高; 交叉变异不定向性则是指交叉变异操作所随机产生的新个体完全有可能比父代个体更差. 由于这两个特点,种群平均适应度并不适合作为中间参考量.
交叉变异不定向性对种群的影响,可以用一个例子简单说明. 设种群适应度向量y=[11,10,10,10,9,9,5],其各元素平均值yavg=9.14. 现假设元素5进行交叉变异操作后得到新值为3. 则新产生种群y′=[11,10,10,10,9,9,3],其平均值y′avg=8.86,若此时仍以平均值作为参考量,则所有元素的相对大小都发生了变化,交叉变异概率需全部进行重新设定. 显然,这种大范围变动是不必要的,甚至会在进化后期影响种群的稳定性.
鉴于此,结合遗传算法选择重复性的特点,本文提出用种群适应度众数作为中间参考量. 种群适应度众数是指种群适应度值中出现次数最多的数值,由于其“数量众多”且相对稳定,交叉变异不确定性很难使适应度众数值改变. 这样既能较好地利用选择重复性的特点,也能更有效地避免不确定性对遗传算子自适应变化产生不良的影响. 为了验证新的种群适应度参考量的有效性,本文仍用式(8)进行仿真,记录下不同时刻种群的适应度平均值、 众数值、 最大值和最小值,结果如表 1所示.
| 运行代数 | 40 | 60 | 80 | 100 |
| 适应度最大值 | 3 738.6 | 3 740.2 | 3 795.1 | 3 852.8 |
| 适应度最小值 | 331.39 | 164.16 | 414.57 | 398.35 |
| 适应度平均值 | 3 077.5 | 2 941.5 | 3 029.1 | 3 144.4 |
| 适应度众数值 | 3 400.2 | 3 610.3 | 3 795.1 | 3 820.8 |
从表 1中的适应度最小值与平均值的变化可以看出,由于进化中经常随机产生“较劣个体”,种群适应度平均值的变化并不稳定,不能较好地描述种群整体适应度值向最优值靠拢的特点. 相反,种群适应度众数值则变化相对稳定,基本不受“较劣个体”的影响,更能代表种群适应度的整体情况,从而证明了本文提出设想的有效性.
4.2 交叉变异概率的自适应调整在自适应调整交叉变异概率的方法中,较为经典的是文[8]提出的AGA(adaptive genetic algorithm)方法,之后,文[11]提出的PAGA(prominent adaptive genetic algorithm)方法也得到了广泛的应用. 设第t代种群中第i个个体将进行交叉变异操作,文[8]中交叉变异概率分别为
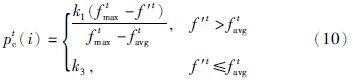
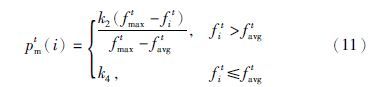
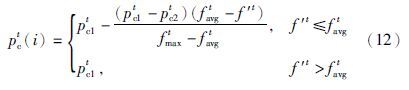
之所以出现上述矛盾,主要是因为这两类方法都没有对整个种群的进化情况进行分析. 在进化初期,种群个体差异较大,交叉概率整体应为较大值,而为了使“优良模式”能够更好地传播,对个体适应度值较大的个体应赋予更大的交叉概率. 在进化后期,交叉操作的效果降低,交叉概率可以适当降低,同时应该更多保留此时的较优个体. 因此,对于适应度值较大的个体,其交叉概率应该更小. 与此同时,变异概率也应该随着种群活力的降低而增大,以避免陷入局部最优解中.
综上所述,本文利用种群活力对算法进程进行判断,设计了一种新的交叉与变异概率的自适应变化规则如下:
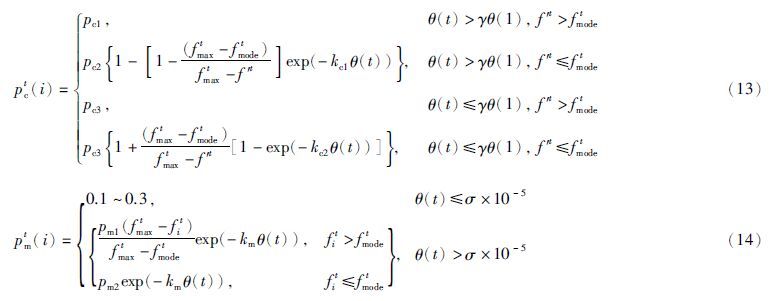
式(13)为交叉概率变化规则,在进化前期,较优个体的“优良模式”能有效传播,而在进化后期,则对较优个体进行保护; 式(14)为变异概率自适应变化规则,其大小随着种群活力降低而升高,同时尽量避免较优个体被破坏. 当种群活力过低时,直接将变异概率设为一较大值,以抑制种群继续变坏,避免陷入局部最优解.
4.3 并行变异操作变异操作通常是在取值范围内产生一个随机数,以此代替原数据,从而使算法能以有一定的概率跳出局部最优解. 但新产生的数据完全是随机的,有时得到的结果对提高收敛精度的影响并不大且不能有效地提高遗传算法的局部寻优能力. 对此,本文提出一种并行变异操作,同时执行两种不同的变异策略,以加快算法收敛速度,提高寻优的精度.
设第t代有某个体x将进行变异操作,则:
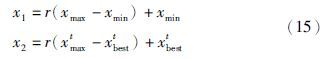
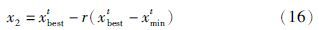
x1是普通变异操作得到的随机值,x2为目前适应度最好的个体附近的一个值. 由于采用实数编码的遗传算法得到的结果可能是靠近最优结果的“较优结果”,因此在算法得到的最优个体xbestt附近,很可能存在更优秀的个体. 很显然,将变异范围缩小在xbestt周围,会增大得到更优解的几率. 需要注意的是,为防止局部收敛,最后比较的是xbestt与x2的适应度值,而不是x1与x2的适应度值. 若xbestt对应的适应度值大,则变异结果取x1,反之以x2为结果. 显然,该方法既保留了普通变异操作避免陷入局部最优解的特点,又通过在已得最优解附近寻找更优解的操作,提高了算法变异性能.
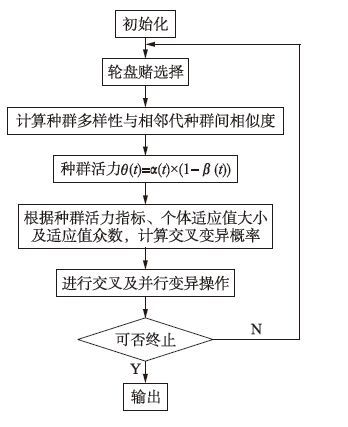
5 算法流程设计的可自适应调节参数的遗传算法实现流程如图 3所示.
步骤1 初始化种群.
步骤2 用轮盘赌方式进行选择操作.
步骤3 计算种群多样性和相邻带种群间相似度.
步骤4 计算种群活力,利用种群活力指标与个体适应度值,确定交叉变异概率.
步骤5 进行交叉操作及并行变异操作.
步骤6 若当前代数小于最大进化代数,则转步骤2: 否则算法终止,返回当前最优解.
|
| 图 3 算法流程图 Fig. 3 Algorithm flow chart |
为了验证本文提出的方法的整体性能,本文选取了3个常用的标称函数,分别用GA算法、 AGA算法、 PAGA算法、 文[13]中提到的HRAGA(adaptive genetic algorithm simulating human reproduction mode)算法、 标准PSO算法及本文的AGAP算法进行仿真对比(各算例种群大小均为100,分别重复测试50次,各函数均设一阈值,达到阈值即可认为收敛).
函数1:
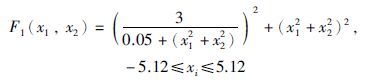
如图 4所示,函数1为Needle-in-a-haystack函数,有4个局部最优解,全局最大值为F1(0,0)=3 600. 该函数在最优解附近分布有许多较差解,具有较大的欺骗性. 本文以3 590作为阈值,不同算法各运行200代,得到结果如表 2、 图 5所示.
|
| 图 4 函数1的三维图像 Fig. 4 Three-dimensional image of function 1 |
| 算法 | 达到阈值平均代数 | 未达到阈值次数 | 平均运行时间 /s | 种群适应度方差 |
| AGA | 98.26 | 18 | 1.081 | 1.093×10-13 |
| PAGA | 104.33 | 13 | 1.084 | 1.788×105 |
| HRAGA | 90.63 | 10 | 1.107 | 3.108×105 |
| PSO | 47.14 | 4 | 2.376 | 2.336×105 |
| AGAP | 64.14 | 8 | 1.544 | 4.079×105 |
表 2为不同算法重复寻优50次的统计结果,图 5为其中一次寻优各算法性能对比曲线. 从二者可以看出,对于二维多极值问题,PSO算法表现最为优异. AGA算法虽然达到阈值需要代数较少,但更容易陷入局部最优解中. PAGA与HRAGA算法寻优能力相似,虽然寻优精度高,但需要更多运行代数. 本文提出的AGAP算法搜索速度更快,跳出局部最优解的能力更强,在寻优性能方面已经接近PSO算法. 需要指出的是,由于对高精度实数取众数,需要消耗较长时间,所以AGAP算法整体用时相对较多. 此外,因为算法会在种群活力较低时提高种群活力,从而使AGAP方差较大,但是其数量级与其它几种算法一致,说明算法提高种群活力的同时,并没有破坏种群的稳定性.
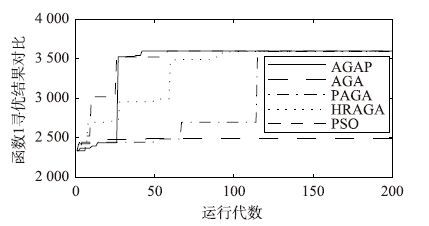
|
| 图 5 函数1不同算法性能对比 Fig. 5 Performance comparison among different algorithms of function 1 |
为进一步证明AGAP相对于其它自适应遗传算法的优越性,本文对各算法进行了基于t检验的假设检验. 以达到阈值的平均代数作为检验对象,不妨将AGAP达到阈值的平均代数作为标准,即μ0=64.14,μ为其它算法达到阈值的平均代数. 若要证明AGAP算法优于其它自适应遗传算法,只需证明在一定的显著性水平下,有μ>μ0即可. 综上所述,置假设H0: μ≤μ0=64.14,H1: μ>μ0=64.14,显著性水平α=0.05. 本文分别用不同的优化算法对函数1再进行25次寻优,所得各算法达到阈值的平均代数μ、 标准差S及结果t如表 3所示.
| μ0=64.14,α=0.05,自由度=24,t0.05/2,24=1.711 | |||
| μ | S | t | |
| AGA | 96.22 | 23.60 | 3.04 |
| PAGA | 100.81 | 16.03 | 5.11 |
| HRAGA | 103.23 | 23.80 | 3.67 |
| PSO | 48.63 | 9.73 | -3.56 |
从表 3可以看出,除PSO算法外,各算法得到的t值均大于t0.05/2,24=1.711,故有理由拒绝H0,而接受H1. 此检验证明了对于函数1,AGAP算法确实优于其它自适应遗传算法,但效果仍不如PSO算法.
函数2:

如图 6所示,函数2为Schaffer函数,有无数个局部极大点,但全局最大值只有一个,即F2(0,0)=1. 此函数在最大值附近有无数局部极值围绕,其值约为0.990 287,一般的寻优算法非常容易陷入局部极值中,因此该函数能较好地检验算法的寻优性能. 本文以0.999作为阈值,不同算法各运行200代,所得结果如表 4、 图 7所示.
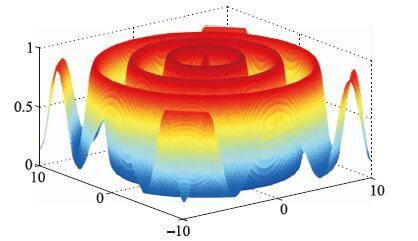
|
| 图 6 函数2的三维图像 Fig. 6 Three-dimensional image of function 2 |
| 算法 | 达到阈值平均代数 | 未达到阈值次数 | 平均算法运行时间 /s | 种群适应度方差 |
| AGA | 102.14 | 17 | 1.058 | 3.994×10-6 |
| PAGA | 109.46 | 12 | 1.084 | 0.018 0 |
| HRAGA | 100.33 | 12 | 1.096 | 0.020 2 |
| PSO | 78.14 | 4 | 0.961 | 0.075 6 |
| AGAP | 77.47 | 7 | 1.308 | 0.034 9 |
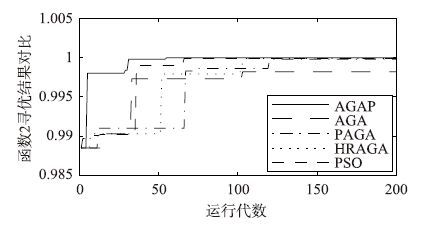
|
| 图 7 函数2不同算法性能对比 Fig. 7 Performance comparison among different algorithms of function 2 |
对比各算法对函数2的优化结果,可以发现与函数1非常相似. 其中,AGA的寻优精度较差,PAGA与HRAGA虽然寻优精度高,但是仍需要更多运行代数; 而AGAP需要的代数较少且寻优精度较高,其效果与PSO算法接近,但明显优于其它自适应遗传算法. 对函数2设计同样的假设检验,置假设H0: μ≤μ0=77.47,H1: μ>μ0=77.47,α=0.05,其结果如下:
从表 5可以看出,除PSO算法外,各算法得到的t值均大于t0.05/2,24=1.711,可以拒绝H0,接受H1. 也即对于函数2,AGAP也优于其它自适应遗传算法,且效果很接近PSO算法.
| μ0=77.47,α=0.05,自由度=24,t0.05/2,24=1.711 | |||
| μ | S | t | |
| AGA | 97.4 | 14.36 | 3.10 |
| PAGA | 98.6 | 15.64 | 3.02 |
| HRAGA | 95.8 | 12.17 | 3.37 |
| PSO | 76.2 | 4.35 | -1.97 |
函数3:
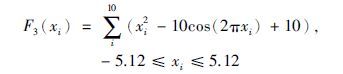
如图 8所示,函数3为Rastrigin函数,是一种多维多峰值函数,在(x1,x2,…,x10)=(0,0,…,0)处可得全局最小值0,而在全局最小值附近,大约有100个局部极小点. 该函数是典型的非线性多模态函数,能较好地检验算法处理高维问题与全局寻优的能力. 本文以0.01作为阈值,对不同算法各运行800代,得到结果如表 6、 图 9所示(为便于观察,图 9只画出前400代比较结果).
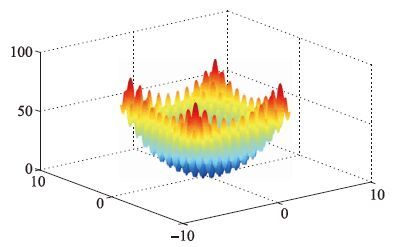
|
| 图 8 函数3的三维图像 Fig. 8 Three-dimensional image of function 3 |
| 算法 | 达到阈值平均代数 | 未达到阈值次数 | 平均算法运行时间 /s | 种群适应度方差 |
| AGA | - | - | 3.177 | 1.20×10-10 |
| PAGA | 618.22 | 15 | 3.275 | 5.31×10-8 |
| HRAGA | 644.63 | 13 | 3.396 | 3.04×10-8 |
| PSO | - | - | 4.747 | 1.68×1048 |
| AGAP | 583.38 | 8 | 4.682 | 6.02×10-8 |
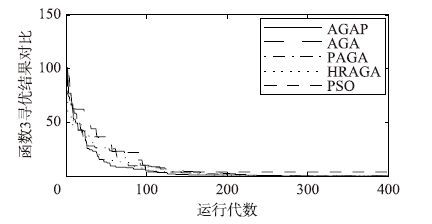
|
| 图 9 函数3不同算法性能对比 Fig. 9 Performance comparison among different algorithms of function 3 |
函数3是高维多极值函数,对优化算法的寻优能力有更高的要求. 由于AGA算法寻优能力不足,导致其在50次测试中,几乎不能达到阈值; 而标准PSO算法本身存在易陷入局部极值的缺点,在解决此类问题时表现较差,也几乎不能达到阈值,且寻优精度较低,以上两点在表 6中均能体现. PAGA、 HRAGA和AGAP算法均能较有效地对函数3寻优,但其中仍以AGAP寻优效果最好,进一步证明了本文算法的有效性. 对函数3再设计相同的假设检验,置假设H0: μ≤μ0=583.38,H1: μ>μ0=583.38,α=0.05,其结果如下:
从表 7可以看出,各算法所得t值均大于t0.05/2,24=1.711,可拒绝H0,接受H1,AGAP确实优于其它算法.
| μ0=583.38,α=0.05,自由度=24,t0.05/2,24=1.711 | |||
| μ | S | t | |
| AGA | - | - | - |
| PAGA | 673.8 | 99.72 | 2.03 |
| HRAGA | 671.6 | 83.00 | 2.37 |
| PSO | - | - | - |
一个有效的优化算法,需要能在不增加任何有针对性改进的情况下,也可以有效解决复杂的实际工业问题. 汽油调和生产近年来越来越受到研究者们的关注[14, 15]. 该问题是一个典型的具有指标约束、 物料平衡约束的多变量非线性规划问题[16, 17, 18],对优化算法的全局寻优能力要求较高,使用一般自适应遗传算法解决此类工业问题往往效果有限. 为了进一步检验AGAP算法相对于其它自适应遗传算法的优越性及其在实际工业问题上的应用效果,本文利用AGAP算法来尝试解决这一问题.
汽油产品质量的指标计算公式分别如下:
研究法辛烷值(RON):
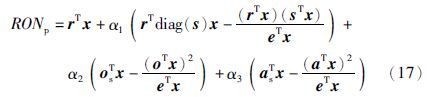
雷德蒸气压(RVP):
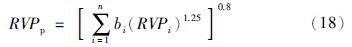
马达法辛烷值(MON):
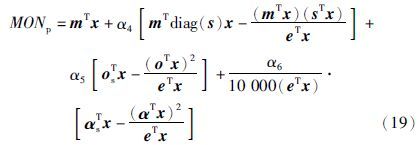
汽油调和最大利润的目标函数如下所示[19]:
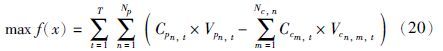
该等式表示汽油调和利润等于调和产品的价值减去各组分油的成本. 其中,T为调和配方的调度时间,Np代表产品的种类,Nc,n代表产品n的组分种类,Cpn,t为产品n的价格,Vpn,t为产品n的调和量,Ccm,t为组分m的成本,Vcn,m,t为产品n中组分m的含量.
调和过程还应遵循以下约束条件:
调和产品的物料平衡约束:
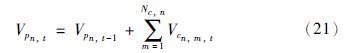
调和产品与调和组分间的物料平衡关系约束:
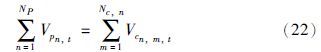
产品各指标(RON、 MON、 RVP)约束:
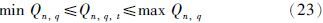
各组分的供应能力约束:
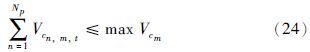
产品需求量约束:
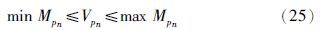
根据表 8可得汽油调和利润函数如下:
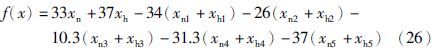
表 9为配方数据相关参数,其中C1、 C2、 C3、 C4、 C5分别代表重整油、 直馏油、 丁烷、 催化油和烷基化油. 利用本文所提出的AGAP算法求解优化后的汽油调和配方及所得利润,并与其它遗传算法结果比较. 其中进化代数为1 000,种群大小为100,pc1、 pc2、 pc3、 pm1、 pm2分别设为0.9、 0.8、 0.7、 0.08、 0.09,γ、 km分别取0.4、 3,kc1、 kc2分别为4、 9,各算法其余条件相同,所得结果如表 10所示.
| 组分油 | C1 | C2 | C3 | C4 | C5 |
| ROM | 94.1 | 70.7 | 93.8 | 92.9 | 95.0 |
| MON | 80.5 | 68.7 | 90.0 | 80.8 | 91.7 |
| 蜡 /% | 1.0 | 1.8 | 0 | 48.8 | 0 |
| 芳烃 /% | 58.0 | 2.7 | 0 | 28.8 | 0 |
| RVP /psi | 3.8 | 12.0 | 138.0 | 5.3 | 6.6 |
| 储量 /(bbl/d) | 12 000 | 6 500 | 3 000 | 4 500 | 7 000 |
| 成本 /($/bbl) | 34.0 | 26.0 | 10.3 | 31.3 | 37.0 |
| 算法 | 产品 | C1 | C2 | C3 | C4 | C5 | RON | MON | RVP | Profit |
| AGA | 普通汽油 | 5 251.22 | 1 830.69 | 84.11 | 773.72 | 60.26 | 90.342 | 79.402 | 8.459 | 66 121.09 |
| 高级汽油 | 4 431.65 | 1 532.36 | 187.98 | 3 594.80 | 253.21 | 91.629 | 80.414 | 10.018 | ||
| PAGA | 普通汽油 | 4 810.66 | 2 502.61 | 95.30 | 548.03 | 43.40 | 88.654 | 78.630 | 9.382 | 67 202.70 |
| 高级汽油 | 3 562.28 | 1 246.81 | 218.44 | 3 743.77 | 1 228.70 | 92.091 | 81.400 | 10.684 | ||
| HRAGA | 普通汽油 | 4 810.66 | 2 502.61 | 95.30 | 548.03 | 43.40 | 88.595 | 78.502 | 9.890 | 69 217.77 |
| 高级汽油 | 3 562.28 | 1 246.81 | 218.44 | 3 743.77 | 1 228.70 | 91.503 | 80.510 | 9.492 | ||
| AGAP | 普通汽油 | 5 094.38 | 2 457.27 | 123.71 | 322.00 | 26.45 | 88.758 | 78.220 | 10.647 | 71 378.21 |
| 高级汽油 | 4 798.98 | 1 568.17 | 201.72 | 3 314.74 | 116.39 | 91.591 | 80.281 | 10.714 |
表 10列举了不同自适应遗传算法对利润目标函数寻优后得到的调和配方,内容包括普通汽油与高级汽油的总量、 每种汽油的各组分含量、 产品的质量指标以及最后所得利润. 从表 10中各方法寻优后的利润与配方对比可以看出,本文提出的AGAP算法表现出更好的寻优能力,得到的优化效益更高,各组分分配方案更加合理,在质量卡边上表现也更优秀,表明AGAP算法相比于其它自适应遗传算法,在不增加任何有针对性的改进的前提下,对解决复杂的多维多约束工业问题有更好的效果,该算法具有较大的工程实践意义.
7 结论本文采用一种新的自适应调节参数的并行变异遗传算法,所提出的算法改变了目前研究中普遍以平均适应度为参考量的做法,结合种群活力评价指标,提出了新的自适应确定交叉变异概率的规则,并引入并行变异思想,从而提高了收敛精度与收敛速度. 3个仿真实例以及汽油调和优化的应用表明,本文算法在实际应用中也能体现出良好性能.
| [1] | Holland J H. Adaptation in natural and artificial system[M]. Ann Arbor, USA: University of Michigan Press, 1975. |
| [2] | 潘立登. 先进控制与在线优化技术及其应用[M]. 北京: 机械工业出版社, 2009. Pan L D. Technology and application of advanced control and online optimization[M]. Beijing, China: Machine Press, 2009. |
| [3] | Yildirim M B, Mouzon G. Single-machine sustainable production planning to minimize total energy consumption and total completion time using a multiple objective genetic algorithm[J]. IEEE Transactions on Engineering Management, 2012, 59(4): 585-597. |
| [4] | Arabali A, Ghofrani M, Etezadi-Amoli M, et al. Genetic-algorithm-based optimization approach for energy management[J]. IEEE Transactions on Power Delivery, 2013, 28(1): 162-170. |
| [5] | Wang L, Tang D. An improved adaptive genetic algorithm based on hormone modulation mechanism for job-shop scheduling problem[J]. Expert Systems with Applications, 2010, 38(6): 7243-7250. |
| [6] | Liu W Z, Ye J H. Collapse optimization for domes under earthquake using a genetic simulated annealing algorithm[J]. Journal of Constructional Steel Research, 2014, 97: 59-68. |
| [7] | Mohammadi-Ivatloo B, Rabiee A, Soroudi A. Nonconvex dynamic economic power dispatch problems solution using hybrid immune-genetic algorithm[J] IEEE Systems Journal, 2013, 7(4): 777-785. |
| [8] | Srinivas M, Patnaik L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on System, Men and Cybernetics, 1994, 24(4): 656-667. |
| [9] | 赵越, 徐鑫, 赵焱, 等. 自适应记忆遗传算法研究[J]. 计算机技术与发展, 2014, 24(2): 63-66. Zhao Y, Xu X, Zhao Y, et al. Research on adaptive memory genetic algorithm[J]. Computer Technology and Development, 2014, 24(2): 63-66. |
| [10] | 王娜, 向凤红, 毛剑琳. 改进的自适应遗传算法求解0/1背包问题[J]. 计算机应用, 2012, 32(6): 1682-1684. Wang N, Xiang F H, Mao J L. Modified adaptive genetic algorithms for solving 0/1 knapsack problems[J]. Journal of Computer Applications, 2012, 32(6): 1682-1684. |
| [11] | 陈世哲, 刘国栋, 浦欣, 等. 基于优势遗传的自适应遗传算法[J]. 哈尔滨工业大学学报, 2007, 39(17): 1021-1024. Chen S Z, Liu G D, Pu X, et al. Adaptive genetic algorithm based on superiority inheritance[J]. Journal of Harbin Institute of Technology, 2007, 39(17): 1021-1024. |
| [12] | Dai X M. Allele gene based adaptive genetic algorithm to the code design[J]. IEEE Transactions on Communications, 2011, 59(5): 1253-1258. |
| [13] | Yan T S. An improved genetic algorithm and its blending application with neural network[C]//2nd International Workshop on Intelligent Systems and Applications. Piscataway, NJ, USA: IEEE, 2010: 1-4. |
| [14] | Zhao J H, Wang N. A bio-inspired algorithm based on membrane computing and its application to gasoline blending scheduling[J]. Computers and Chemical Engineering, 2011, 35(2): 272-283. |
| [15] | Singh A, Forbes J F, Vermeer P J, et al. Model-based real-time optimization of automotive gasoline blending operations[J]. Journal of Process Control, 2000, 10(1): 43-58. |
| [16] | 陈霄, 王宁. 一种新的DNA遗传算法及其在参数估计中的应用[J]. 化工学报, 2010, 61(8): 1912-1918. Chen X, Wang N. A new DNA genetic algorithm and its application in parameter estimation[J]. CIESC Journal, 2010, 61(8): 1912-1918. |
| [17] | 王继东, 王万良. 基于遗传算法的汽油调和生产优化研究[J]. 化工自动化及仪表, 2005, 32(1): 6-9. Wang J D, Wang W L. Research of gasoline blending optimization based on genetic algorithm[J]. Control and Instruments in Chemical Industry, 2005, 32(1): 6-9. |
| [18] | Litvinenko V I, Burgher J A, Vyshemirskij V S, et al. Application of genetic algorithm for optimization gasoline fractions blending compounding[C]//Proceedings of the 2002 IEEE International Conference on Artificial Intelligence Systems. Piscataway, NJ, USA: IEEE 2002: 391-394. |
| [19] | 张建明, 冯建华. 两群微粒群算法及其在油品调和优化中的应用[J]. 化工学报, 2008, 59(7): 1721-1726. Zhang J M, Feng J H. Gasoline blending recipe optimization based on two particle swarms optimization[J]. CIESC Journal, 2008, 59(7): 1721-1726. |
| [20] | 赵进慧, 柴天佑, 周平. 改进的膜计算仿生优化算法及在汽油调和中的应用[J]. 化工学报, 2012, 63(9): 2965-2971. Zhao J H, Chai T Y, Zhou P. Modified bio-inspired algorithm based on membrance computing and application in gasoline blending[J]. CIESC Journal, 2012, 63(9): 2965-2971. |



