2. 江南大学“轻工过程先进控制”教育部重点实验室,江苏 无锡 214122
2. Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), Jiangnan University, Wuxi 214122, China
时滞在实际系统(如热工系统,化工过程等)中普遍存在,且在很多情况下未知,而时滞对系统的控制有较大影响; 另外,在系统模型已知的情况下,参数辨识是对系统进行控制的前提; 因此参数和时滞的辨识具有十分重要的实际意义[1, 2]. 通常,辨识系统参数前,要预先估计出系统时滞. 但是,对于具有大时滞的多输入单输出(multiple-input single-output,MISO)系统,常用的时滞估计方法可能会有较大的近似误差[3, 4]. 此外,采用常规算法辨识参数[5, 6, 7]和时滞时需要大量的采样数据,增加了采样成本. 因此,对于含有较大时滞的多变量系统,为了提高辨识效率,找到一种能够在有限的采样数据下有效辨识系统参数和时滞的方法是非常必要的.
实际系统中模型的阶次通常较低,也就是说,对于含有较大时滞的多变量系统,参数化得到的高维参数向量中仅含有少量非零参数且非零参数的位置未知,这样的参数向量称为稀疏向量; 由稀疏向量表示的系统称为稀疏系统[8, 9, 10]. 压缩感知(compressed sensing,CS)理论[11, 12, 13, 14, 15]是研究稀疏系统的一种重要理论,CS重构理论能够根据低维的观测数据和测量矩阵重构未知的高维稀疏信号[16, 17]; 在许多领域基于该理论对稀疏系统已经进行了深入的研究[18, 19],然而在控制理论的研究还不多,文[8]针对含有时滞的确定性ARX(Auto Regressive with eXternal input)模型,在有限采样数据量下采用分块正交匹配追踪算法辨识系统参数和时滞; 文[20]针对含有时滞的单输入单输出ARX模型,在有限的采样数据量下提出了一种l1正则化算法辨识系统参数和时滞; 文[21]针对噪声干扰中存在离群点的情况,采用基于压缩感知的方法对系统进行辨识.
本文针对含有未知时滞的多输入单输出有限脉冲响应系统,研究在有限的采样数据量下参数和时滞的辨识问题,提出一种梯度追踪算法,同时估计系统的参数和时滞. 文[8]中采用分块正交匹配追踪算法估计系统的非零参数,但该算法需要计算协方差矩阵,特别是当协方差矩阵维数较大时,计算量较大[22]. 针对这一问题,本文考虑将匹配追踪思想和梯度搜索方法相结合以避免求解协方差矩阵,从而减小计算量,提高辨识效率.
2 系统描述考虑如下MISO-FIR系统:
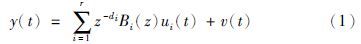
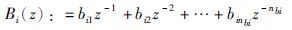
若不直接考虑时滞di,定义:
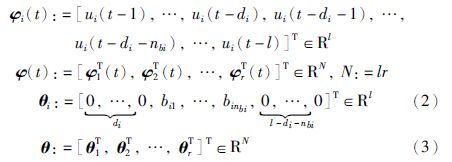
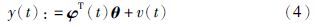
当有m组采样数据,即t=1,2,…,m时,定义:
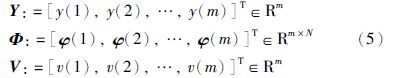

如果m$ \gg $N,可采用最小二乘方法直接得到参数向量的估计:
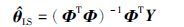
然而,式(6)中参数向量θ的维数N较高,若采用最小二乘算法将耗费大量的采样时间,增加辨识成本. 本文将压缩感知重构理论应用于该系统的辨识,仅需要有限的采样数据量(甚至m<N),即可有效地估计系统的参数和时滞.
3 梯度追踪算法根据压缩感知重构,稀疏系统(6)的辨识问题可描述为
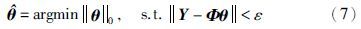
令φi表示信息矩阵Φ的第i列; θi表示参数向量θ的第i个参数; 式(6)中输出向量Y可改写为信息矩阵各列的线性组合加噪声向量的形式,即:
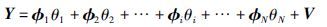
令k=1,2,…为迭代变量,λk为第k次迭代选出φi的索引,索引集Λk={λ1,…,λk}; ΦΛk为Λk指示的φi所构成的信息矩阵; ${\hat \theta }$k表示第k次迭代得到的参数估计; ${\hat \vartheta }$k∈RN是根据Λk的指示由${\hat \theta }$k恢复的参数估计,${\hat \vartheta }$0=0; 每次迭代的残差用rk表示,初始残差r0=Y,残差rk由下式计算:

定义准则函数:
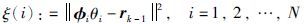
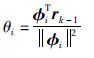
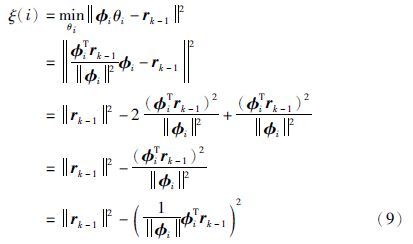
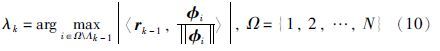

定义准则函数:
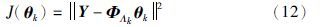
应用最小二乘原理,将J(θk)对θk求导并令其为0,则有:
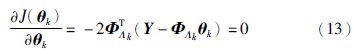
由式(13)可得第k次迭代的参数估计:
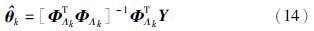
根据得到的${\hat \theta }$k,由式(8)更新残差rk. 然后按照Λk的指示将${\hat \theta }$k恢复为N维的参数向量${\hat \vartheta }$k,并同${\hat \vartheta }$k-1比较,若║${\hat \vartheta }$k-${\hat \vartheta }$k-1║>ε0(式中ε0>0为设定的允许误差),则令k=k+1继续迭代; 否则停止迭代,得到参数估计k.
值得注意的是,用${\hat \theta }$k代替式(13)中的θk,并将式(8)代入式(13),则有:
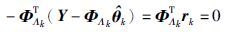
采用负梯度搜索原理极小化J(θk)得
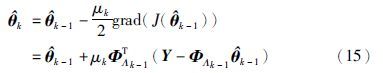
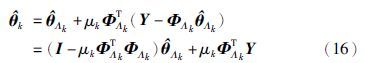
为使${\hat \theta }$k收敛,式(14)中[I-μkΦTΛkΦΛk]的所有特征值都应在单位圆内,文[23]给出了迭代步长μk的范围,一种可行的保守方法是迭代步长μk满足:
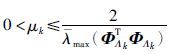
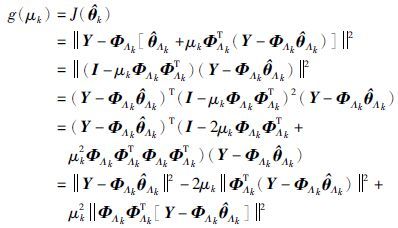
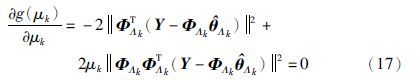
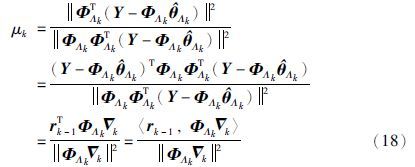
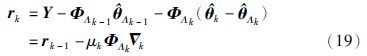
(1) 收集有限的输入输出数据{ui(t),y(t): i=1,2,…,r; t=1,2,…,m},设定参数估计精度ε0.
(2) 由式(5)构造堆积输出向量Y,信息矩阵Φ.
(3) 令k=k+1,设置初值,令r0=Y,Λ0=∅,${\hat \vartheta }$0=0.
(4) 根据式(10)确定索引λk,并根据式(11)更新集合Λk,由Λk获取子信息矩阵ΦΛk.
(5) 根据Λk由${\hat \vartheta }$k构造${\hat \theta }$Λk.
(6) 由式(18)计算第k次的迭代步长μk,由式(16)计算第k次迭代的参数估计${\hat \theta }$k; 根据Λk将${\hat \theta }$k恢复为N维的${\hat \vartheta }$k.
(7) 比较${\hat \vartheta }$k和${\hat \vartheta }$k-1,如果║${\hat \vartheta }$k-${\hat \vartheta }$k-1║>ε0由式(16)更新残差rk,令k=k+1回到步骤(4)继续迭代; 否则迭代停止,获得参数估计向量${\hat \vartheta }$k.
根据得到的参数估计值${\hat \vartheta }$∈RN,结合输入通道的数据回归长度l以及阶次nbi,则可估计出系统每个输入通道的时滞. 由式(2)、 式(3)可知,中共有r+1个零元素块,用ni(i=1,2,…,r+1)表示零元素块中零元的个数,则输入通道的时滞估计为
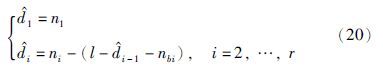
收敛性分析是辨识算法研究的一项重要内容. 本小节给出GP算法的收敛性能及其计算量分析.
定理1 对于GP算法(10),式(16)~式(19),在每次迭代中总存在依赖于子信息矩阵ΦΛk的常数0<ck<1,使得下式成立:
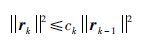
证明 式(19)等号两边取范数的平方可得[24]
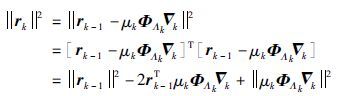
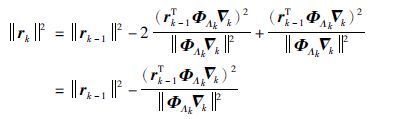
由于$\nabla $k=ΦTΛkrk-1,根据矩阵范数的相容性,上式可写为
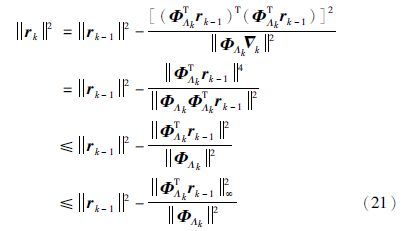
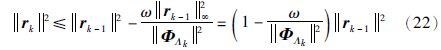
与OMP算法相比,GP算法每次迭代不需要计算协方差矩阵Sk=(ΦTΛkΦΛk)-1,因而有较小的计算量. OMP算法和GP算法的计算量如表 1所示.
| 算法 | 计算步骤 | 乘法计算量 | 加法计算量 |
| OMP | Sk:=ΦTΛkΦΛk | mk2 | k2(m-1) |
| Sk′:=S-1k | k3 | k3-k2 | |
| βk:=ΦTΛkY | mk | k(m-1) | |
| ${\hat \theta }$k=Sk′βk | k2 | k(k-1) | |
| rk=Y${\bar \varphi }$Λk${\hat \theta }$k | mk | mk | |
| 加法或乘法的总计算量 | k3+k2+(k2+2k)m | k3+(k2+2k)(m-1) | |
| 全部计算量: N1 | 2k3+2mk2+4mk-2k | ||
| GP | $\nabla $k=ΦTΛk(Y${\bar \varphi }$ΛkΛk) | 2mk | (2m-1)k |
| Gk=ΦΛk$\nabla $k | mk | (k-1)m | |
| μk=〈rk-1,Gk〉/║Gk║2 | 2m+1 | 2(m-1) | |
| ${\hat \theta }$k=${\hat \theta }$Λk+μk$\nabla $k | k | k | |
| rk=rk-1-μkGk | m | m | |
| 加法或乘法的总计算量 | (3m+1)(k+1) | 3mk+2m-2 | |
| 全部计算量: N2 | 6mk+5m+k-1 | ||
| 计算量差值: V:=N1-N2 | k(2k2-3)+m(2k2-2k-5)+1 | ||
考虑如下MISO-FIR系统:
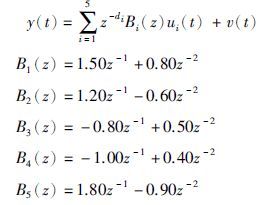
系统各输入通道的时滞分别为d1=20,d2=3,d3=32,d4=47,d5=10. l=50,系统的参数向量为
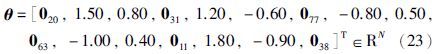
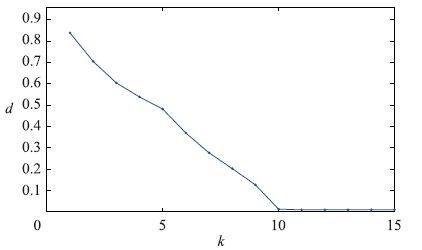
仿真时,输入ui(t)采用随机不相关的零均值单位方差信号,噪声v(t)采用均值为零方差为σ2的白噪声序列. 定义参数估计误差δ:=║θ-${\hat \vartheta }$k║/║θ║. 取采样数据长度m=200,噪声方差为σ2=0.102,分别采用OMP算法和GP算法辨识系统,参数估计误差δ随迭代次数k的变化如表 2所示; GP算法的参数估计误差δ随迭代次数k的变化如图 1所示.
| 算法 | k | b11 | b12 | b21 | b22 | b31 | b32 | b41 | b42 | b51 | b52 | δ /% |
| 1 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 1.609 5 | 0.000 0 | 83.850 2 | |
| 2 | 1.339 9 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 1.569 9 | 0.000 0 | 70.602 9 | |
| OMP | 5 | 1.375 9 | 0.881 3 | 1.248 4 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 1.653 6 | -0.968 8 | 47.753 1 |
| 10 | 1.504 8 | 0.801 8 | 1.209 9 | -0.606 0 | -0.786 9 | 0.495 1 | -1.009 3 | 0.407 8 | 1.804 7 | -0.902 7 | 0.702 5 | |
| 15 | 1.506 9 | 0.803 9 | 1.209 5 | -0.610 0 | -0.785 4 | 0.494 6 | -1.009 9 | 0.411 8 | 1.804 6 | -0.901 2 | 0.836 7 | |
| 1 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 1.609 5 | 0.000 0 | 83.850 2 | |
| 2 | 1.338 7 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 1.609 5 | 0.000 0 | 70.496 2 | |
| GP | 5 | 1.366 2 | 0.863 6 | 1.265 3 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 1.548 5 | -0.942 0 | 48.146 9 |
| 10 | 1.509 1 | 0.820 0 | 1.190 8 | -0.587 0 | -0.824 9 | 0.487 5 | -0.993 9 | 0.396 1 | 1.795 3 | -0.907 0 | 1.232 2 | |
| 15 | 1.510 5 | 0.818 2 | 1.190 6 | -0.587 0 | -0.804 1 | 0.490 2 | -0.993 5 | 0.394 5 | 1.798 5 | -0.904 8 | 0.917 2 | |
| 真值 | 1.500 0 | 0.800 0 | 1.200 0 | -0.600 0 | -0.800 0 | 0.500 0 | -1.000 0 | 0.400 0 | 1.800 0 | -0.900 0 |
|
| 图 1 GP算法的参数估计误差δ随迭代次数k的变化(m=200,σ2=0.102) Fig. 1 The parameter estimation errors δ of the GP algorithm vs. k(m=200,σ2=0.102) |
梯度追踪算法得到的稀疏参数向量如表 3所示,最终辨识得到的参数估计为
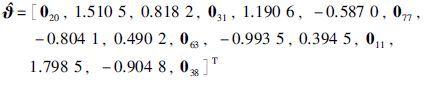
表 3中第一行是辨识得到的稀疏参数向量中非零参数的位置,中零元素块的数目分别为n1=20,n2=31,n3=77,n4=63,n5=11,n6=38. 结合式(20)可得系统的时滞估计为
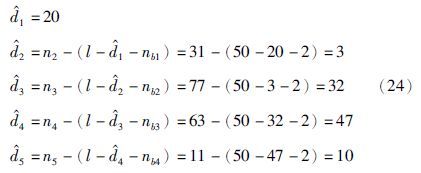
| 参数位置 | 21 | 22 | 54 | 55 | 133 | 134 | 198 | 199 | 211 | 212 |
| 参数值 | 1.510 5 | 0.818 2 | 1.190 6 | -0.587 0 | -0.804 1 | 0.490 2 | -0.993 5 | 0.394 5 | 1.798 5 | -0.904 8 |
定义节约的计算量为η:=$\frac{{{N_1} - {N_2}}}{{{N_1}}}$×100%. 当k=15时,OMP算法和GP算法的计算量以及η分别为
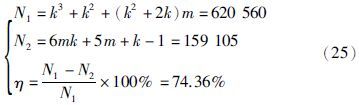
综合表 1、 表 2、 图 1,式(24)和式(25)可知:
(1) GP算法和OMP算法的参数估计误差随迭代次数k的增加都逐渐减少,最终趋于稳定;
(2) 该稀疏系统在有限采样数据量下,GP算法的辨识精度接近OMP算法,见表 2;
(3) GP算法能够在有效估计系统参数的同时还能有效地估计系统的未知时滞$\hat{d}$i;
(4) GP算法能够有效地减少计算量,见式(25).
6 结论针对含有未知时滞的MISO-FIR系统的参数与时滞辨识问题,本文提出了一种梯度追踪算法辨识系统参数和时滞,对于大时滞的系统,该算法可以在有限的采样数据下同时估计出系统的参数与时滞. 性能分析表明该算法收敛且具有较小的计算量. 数值仿真验证了算法的有效性.
| [1] | Ljung L. System identification: Theory for the user[M]. 2nd ed. Englewood Cliffs, NJ, USA: Prentice-Hall, 1999. |
| [2] | 丁锋. 系统辨识新论[M]. 北京: 科学出版社, 2013: 1-33. Ding F. System identification - New theory and methods[M]. Beijing: Science Press, 2013: 1-33. |
| [3] | Unbehauen H, Rao G P. Continuous-time approaches to system identification - A survey[J]. Automatica, 1990, 26(2): 23-25. |
| [4] | 王建宏, 王道波, 王志胜. 多个未知时延的MISO系统的递推辨识[J]. 控制与决策, 2010, 25(1): 93-98. Wang J H, Wang D B, Wang Z S. Recursive identification of MISO systems with multiple unknown time delays[J]. Control and Decision, 2010, 25(1): 93-98. |
| [5] | Ding F. Hierarchical multi-innovation stochastic gradient algorithm for Hammerstein nonlinear system modeling[J]. Applied Mathematical Modelling, 2013, 37(4): 1694-1704. |
| [6] | Liu Y J, Ding F, Shi Y. An efficient hierarchical identification method for general dual-rate sampled-data systems[J]. Automatica, 2014, 50(3): 962-970. |
| [7] | Ding J, Ding F, Liu X P, et al. Hierarchical least squares identification for linear SISO systems with dual-rate sampled-data[J]. IEEE Transactions on Automatic Control, 2011, 56(11): 2677-2683. |
| [8] | Sanandaji B M, Vincent T L, Wakin M B, et al. Compressive system identification of LTI and LTV ARX models[C]//50th IEEE Conference on Decision and Control and European Control Conference. Piscataway, NJ, USA: IEEE, 2011: 791-798. |
| [9] | Tropp J A. Just relax: Convex programming methods for identifying sparse signals in noise[J]. IEEE Transactions on Information Theory, 2006, 52(3): 1030-1051. |
| [10] | Elad M. Sparse and redundant representations: From theory to applications in signal and image processing[M]. Berlin, Germany: Springer-Verlag, 2010. |
| [11] | Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. |
| [12] | Candès E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. |
| [13] | Baraniuk R. A lecture on compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. |
| [14] | 李树涛, 魏丹. 压缩传感综述[J]. 自动化学报, 2009, 35(11): 1369-1377. Li S T, Wei D. A survey on compressive sensin[J]. Acta Automatica Sinica, 2009, 35(11): 1369-1377. |
| [15] | 石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081. Shi G M, Liu D H, Gao D H, et al. Advances in theory and application of compressed sensing[J]. Acta Electronica Sinica, 2009, 37(5): 1070-1081. |
| [16] | Candès E J. Robust uncertainty principles: Extra signal reconstruction from highly frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. |
| [17] | Candès E J, Romberg J R, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223. |
| [18] | Haupt J, Bajwa W, Raz G, et al. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J]. IEEE Transactions on Information Theory, 2010, 56(11): 5862-5875. |
| [19] | Tropp J A. Greed is good: Algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. |
| [20] | Tóth R, Sanandaji B M, Poolla K, et al. Compressive system identification in the linear time-invariant framework[C]//50th IEEE Conference on Decision and Control and European Control Conference. Piscataway, NJ, USA: IEEE, 2011: 783-790. |
| [21] | Xua W Y, Bai E W, Choa M. System identification in the presence of outliers and random noises: A compressed sensing approach[J]. Automatica, 50(11): 2905-2911. |
| [22] | Cai T T, Wang L. Orthogonal matching pursuit for sparse signal recovery with noise[J]. IEEE Transactions on Information Theory, 2011, 57(7): 4680-4688. |
| [23] | Ding F, Liu X P, Liu G. Gradient based and least-squares based iterative identification methods for OE and OEMA systems[J]. Digital Signal Processing, 2010, 20(3): 664-677. |
| [24] | Blumensath T, Davies M E. Gradient pursuits[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2370-2382. |
| [25] | Mallat S. A wavelet tour of signal processing[M]. London, UK: Academic Press, 1999. |



