优化技术是一种以数学为基础,用于求解各种工程问题最优解或满意解的应用技术. 智能优化算法是一种新兴的优化算法,是最受关注的优化研究领域之一,已成为优化计算的重要研究方向. 量子智能优化算法可分为量子衍生优化和量子行为优化算法. 就量子行为优化算法而言,目前国际上最为流行的是我国学者孙俊提出的量子行为粒子群优化(quantum-behaved particle swarm optimization,QPSO)算法[1]. 该算法的基本原理是通过模拟量子力学中粒子在势场中向势能最低点的移动建立搜索机制,即将粒子寻优空间看作量子力学中的势阱,将全局最优解看作势场中势能最低点(势阱中心),将粒子的寻优过程看作势场中粒子向势能最低点的移动过程.
目前国内外学者对QPSO开展的改进研究主要集中于控制参数设计、 算法自身改进与其它算法融合3个方面. 在控制参数设计方面,文[2]通过严格的理论证明得出该收缩因子必须小于1.781才能保证算法收敛. 文[3]提出了基于种群多样性的收缩因子自适应设计方法. 在算法自身改进方面,文[4]运用概率度量空间理论,首次对QPSO的收敛行为给出了深入系统的分析. 文[5, 6, 7]采用高斯分布产生的随机数代替原算法中均匀分布产生的随机数. 文[8]提出了在QPSO中增加局部搜索的新方法. 在与其它算法融合方面,文[9]结合遗传算法的精英保留策略和模拟退火算法容易跳出局部最优的能力,提出了一种改进算法. 文[10, 11]提出了基于差分变异的QPSO算法. 文[12, 13]提出了在QPSO算法中利用混沌序列来产生变异的进化策略.
尽管QPSO目前已有很多改进,然而根据没有最好只有更好的原则,该算法仍有改进的余地和必要. 在QPSO中,势阱中心代表着寻优方向,起着优化路标的作用,本文提出了新的势阱中心设计方法; 同时,本文也提出了一个新的粒子位置更新式. 实验结果验证了新算法的优势.
2 量子行为粒子群算法根据量子力学原理,粒子动态行为可用如下薛定谔方程描述[14]:

下面以Delta势阱为例说明QPSO的构造过程. Delta势阱的势能分布为V(r)=-γδ(r),代入式(1),可解出粒子的波函数为


势阱中粒子的行为服从薛定谔方程,在任意时刻的位置是不确定的,而普通粒子服从牛顿力学,在任意时刻必须具有确定的位置. 这一矛盾可采用蒙特卡洛方法解决. 首先在(0,1)内取随机数u,然后令u=e-2|r|/L,最后解出|r|=ln(u-1)L/2. 由此可得

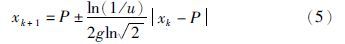
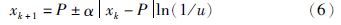
本文提出的改进的量子行为粒子群优化(improved QPSO,IQPSO),其改进措施主要是针对势阱中心的设计进行的. 现有的QPSO采用如下迭代式[15]:

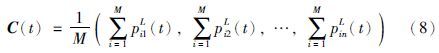
这种迭代的不足在于: 在优化的后期阶段作为优化路标的势阱中心的引领作用不够明显.
本文提出的改进措施,其基本思想可描述为: 在每步迭代中,作为势阱中心的粒子,都来源于一个当代构造的最优解候选集,在该集合中采用轮盘赌随机选取.
最优解候选集根据当代种群适应度择优选取前Kbest个粒子构成. 众所周知,在算法初期,重点在于全局探索,而在算法后期,重点在于局部开发. 因此,为平衡算法的探索和开发能力,候选集中粒子的数目Kbest随迭代步数单调减小. 具体如式(9)所示:
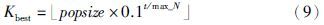
另外,为增强种群多样性,使算法避免早熟收敛,本文基于当代种群所有粒子的平均值(中心粒子)设计了一个新的位置更新式. 该式的作用为: 使粒子等概率地向着中心粒子或偏离中心粒子移动.
记第t代用轮盘赌选择的粒子为Xbest(t),种群平均粒子为Xmean(t)=$\frac{1}{{popsize}}\sum\limits_{i = 1}^{popsize} {} $Xi(t),本文采用随机选择如下两式之一更新粒子位置:
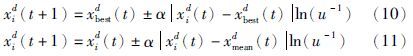
关于以上两式的合理性,给出如下解释: (1)在根据势阱理论得到的迭代式(6)中,只需将势阱中心P替换为最优粒子xbestd即可得到式(10),在势阱中,粒子向着势阱中心移动,而模拟此现象的式(10),使粒子向着最优粒子移动,因此式(10)是合理的. (2)在式(11)中,α前面的正负号等概率地随机选取,该式的作用效果可表述为式(12):

在迭代过程中,若单纯使用式(10),则很容易导致早熟收敛. 由于式(10)和式(11)等概率随机选取,两式中的正负号也等概率随机选取,因此式(11)的独特之处在于允许粒子以1/4的概率偏离平均粒子,从而能够在一定程度上抑制早熟收敛. 因此式(11)是合理的.
由式(9)~(11)可知,在本文提出的IQPSO中,除了种群规模、 变量维数、 迭代步数等所有智能优化算法都需要事先设定的共性参数外,体现算法自身特性的控制参数,并没有增加,仍然只有一个α.
值得指出IQPSO与现有QPSO[8]有两点不同:
(1) 在IQPSO中,每步迭代用作势阱中心的粒子来自于由前Kbest个适应度最大粒子组成的候选集,具体采用哪个粒子由轮盘赌策略决定; 而QPSO自始至终分别采用自身最优粒子和自身最优粒子的算术平均作为势阱中心.
(2) 关于粒子位置的更新,IQPSO除采用由量子势阱建模得到的更新式外,还采用了另一个类似的更新式,每步迭代,两个公式等概率随机选择使用.
本文提出的IQPSO的算法流程可简述如下:
(1) 种群及参数初始化.
(2) 计算个体适应度.
(3) 按式(9)更新Kbest,建立最优解候选集.
(4) 采用轮盘赌策略在候选集中选择一个粒子作为势阱中心.
(5) 在式(10)和式(11)中,等概率选择其一,产生下一代个体.
(6) 重复步骤(2)~(5)直到满足终止条件.
4 在函数极值优化中的应用 4.1 测试函数采用CEC2013定义的28个标准函数作为优化对象[16],如表 1所示. 其中,函数名称后面的“(S)”表示该函数的变量是可分离的,“(N)”表示变量是不可分离的. 函数21~28名称后面的n表示该函数由其它n个基本函数复合而成. D为优化空间维数. 所有函数均为极小值优化.
| 序号 | 名称 | 最小值 | |
| 单峰函数 | 1 | Sphere (S) | -1 400 |
| 2 | Rotated High Conditioned Elliptic (N) | -1 300 | |
| 3 | Rotated Bent Cigar (N) | -1 200 | |
| 4 | Rotated Discus (N) | -1 100 | |
| 5 | Different Powers (S) | -1 000 | |
| 基本多峰函数 | 6 | Rotated Rosenbrock′s (N) | -900 |
| 7 | Rotated Schaffers F7 (N) | -800 | |
| 8 | Rotated Ackley′s (N) | -700 | |
| 9 | Rotated Weierstrass (N) | -600 | |
| 10 | Rotated Griewank′s (N) | -500 | |
| 11 | Rastrigin′s (S) | -400 | |
| 12 | Rotated Rastrigin′s (N) | -300 | |
| 13 | Non-Continuous Rotated Rastrigin′s (N) | -200 | |
| 14 | Schwefel′s (N) | -100 | |
| 15 | Rastrigin′s Schwefel′s (N) | 100 | |
| 16 | Rotated Katsuura (N) | 200 | |
| 17 | Lunacek Bi_Rastrigin (S) | 300 | |
| 18 | Rotated Lunacek Bi_Rastrigin (N) | 400 | |
| 19 | Expanded Griewank′s plus Rosenbrock′s (N) | 500 | |
| 20 | Expanded Scaffer′s F6 (N) | 600 | |
| 复合函数 | 21 | Composition Function 1 (n=5,Rotated) (N) | 700 |
| 22 | Composition Function 2 (n=3,Unrotated)(S) | 800 | |
| 23 | Composition Function 3 (n=3,Rotated) (N) | 900 | |
| 24 | Composition Function 4 (n=3,Rotated) (N) | 1 000 | |
| 25 | Composition Function 5 (n=3,Rotated) (N) | 1 100 | |
| 26 | Composition Function 6 (n=5,Rotated) (N) | 1 200 | |
| 27 | Composition Function 7 (n=5,Rotated) (N) | 1 300 | |
| 28 | Composition Function 8 (n=5,Rotated) (N) | 1 400 | |
| 搜索范围: [-100,100]D | |||
为体现提出算法的优良性能,所有函数的优化结果将与文[15]中的量子行为粒子群算法(QPSO)对比,同时也与引力搜索算法(gravitational search algorithm,GSA)和差分进化算法(differential evolution,DE)对比. 引力搜索算法是2009年提出的一种源于对物理学中的万有引力进行模拟的新的优化搜索技术[17],它优于许多现有的智能优化算法,因此可作为测试本文算法性能的参照物.
为保证对比客观公正,IQPSO、 QPSO、 GSA、 DE采用相同的种群规模和迭代步数(即函数评估次数). 为尽量消除对比结果的随机性并增强对比结果的可信度,所有函数均取D=10维和D=30维两种情况,且每个函数均用4种算法各自独立优化30次,取30次优化的平均结果作为对比指标.
4种算法的共性参数设置如下: 当D=10时,种群规模取30; 当D=30时,种群规模取50,终止条件为限定迭代步数,两种维数下的迭代步数均取1 000.
对于IQPSO的个性参数经过多次实验,当D=10时,取α=0.4; 当D=30时,取α=0.3. GSA的个性参数有两个,经过多次实验,万有引力常数G的初值取G0=100,G单调下降的指数因子取α=10; QPSO的控制参数取α=0.5. DE的缩放因子F=0.5,交叉概率CR=0.8.
4.3 优化结果对比所有实验均在配置Intel(R) Core(TM) i5-3470 CPU 3.20 GHz处理器、 4.00 GB内存、 Window 7操作系统的计算机上,采用Matlab 7.0编程实现. 当D=10和D=30时,IQPSO与QPSO的优化结果对比如表 2所示,IQPSO和GSA的优化结果对比如表 3所示. IQPSO和DE的优化结果对比如表 4所示. 表中粗体表示对比结果获胜.
| 序号 | D=10 | D=30 | ||
| IQPSO | QPSO | IQPSO | QPSO | |
| 1 | -1 400 | -1 400 | -1 400 | -1 399.99 |
| 2 | 1.289E+6 | 2.336E+6 | 1.286E+7 | 3.471E+7 |
| 3 | 2.272E+6 | 9.853E+7 | 5.019E+7 | 8.699E+9 |
| 4 | 3.445E+4 | 1.008E+4 | 1.192E+5 | 5.671E+4 |
| 5 | -1 000 | -1 000 | -1 000 | -999.910 |
| 6 | -887.677 | -881.479 | -850.223 | -804.190 |
| 7 | -798.826 | -764.098 | -791.202 | -699.493 |
| 8 | -678.875 | -679.572 | -678.608 | -678.968 |
| 9 | -596.532 | -593.335 | -585.435 | -563.867 |
| 10 | -499.148 | -498.655 | -495.840 | -484.218 |
| 11 | -393.234 | -387.112 | -379.736 | -240.425 |
| 12 | -290.995 | -271.720 | -233.630 | -64.566 9 |
| 13 | -175.726 | -168.709 | -112.452 | 46.018 91 |
| 14 | 15.040 35 | 971.510 6 | 469.649 7 | 6 635.491 |
| 15 | 757.249 5 | 1 418.186 | 6 206.506 | 7 537.068 |
| 16 | 204.992 1 | 201.379 0 | 206.935 2 | 202.988 8 |
| 17 | 317.964 5 | 331.484 7 | 357.369 6 | 520.570 2 |
| 18 | 482.609 7 | 440.269 5 | 688.390 2 | 658.776 6 |
| 19 | 501.064 1 | 501.831 9 | 503.668 2 | 516.610 4 |
| 20 | 604.265 3 | 603.436 9 | 614.972 1 | 614.779 8 |
| 21 | 1 073.501 | 1 100.199 | 1 031.182 | 1 062.422 |
| 22 | 959.052 6 | 2 161.369 | 1 328.177 | 7 825.982 |
| 23 | 1 604.993 | 2 582.605 | 5 872.228 | 9 139.212 |
| 24 | 1 207.599 | 1 186.178 | 1 224.665 4 | 1 251.876 |
| 25 | 1 305.289 | 1 308.323 | 1 364.422 2 | 1 401.211 |
| 26 | 1 392.971 | 1 361.473 | 1 526.175 3 | 1 409.171 |
| 27 | 1 658.575 | 1 700.131 | 1 866.358 1 | 2 310.194 |
| 28 | 1 700 | 1 945.288 | 1 700.001 3 | 1 877.659 |
| 序号 | D=10 | D=30 | ||
| IQPSO | GSA | IQPSO | GSA | |
| 1 | -1 400 | -1 400 | -1 400 | -1 400 |
| 2 | 1.289E+6 | 1.084E+6 | 1.286E+7 | 7.501E+6 |
| 3 | 2.272E+6 | 5.278E+7 | 5.019E+7 | 5.886E+9 |
| 4 | 3.445E+4 | 1.931E+4 | 1.192E+5 | 7.034E+4 |
| 5 | -1 000 | -1 000 | -1 000 | -999.997 |
| 6 | -887.677 | -886.419 | -850.223 | -838.203 |
| 7 | -798.826 | -777.634 | -791.202 | -727.061 |
| 8 | -678.875 | -678.857 | -678.608 | -678.636 |
| 9 | -596.532 | -596.242 | -585.435 | -565.943 |
| 10 | -499.148 | -499.993 | -495.840 | -499.857 |
| 11 | -393.234 | -377.381 | -379.736 | -67.189 3 |
| 12 | -290.995 | -279.470 | -233.630 | 94.859 60 |
| 13 | -175.726 | -161.715 | -112.452 | 346.629 9 |
| 14 | 15.040 35 | 765.634 | 469.649 7 | 3 983.880 |
| 15 | 757.249 5 | 592.721 3 | 6 206.506 | 3 855.685 |
| 16 | 204.992 1 | 200.013 3 | 206.935 2 | 200.011 7 |
| 17 | 317.964 5 | 314.885 | 357.369 6 | 411.101 2 |
| 18 | 482.609 7 | 415.709 5 | 688.390 2 | 502.584 4 |
| 19 | 501.064 1 | 501.161 2 | 503.668 2 | 513.043 8 |
| 20 | 604.265 3 | 604.769 4 | 614.972 1 | 615.000 0 |
| 21 | 1 073.501 | 1 100.193 | 1 031.182 | 1 057.418 |
| 22 | 959.052 6 | 2 565.500 | 1 328.177 | 7 144.644 |
| 23 | 1 604.993 | 2 218.428 | 5 872.228 | 6 819.483 |
| 24 | 1 207.599 | 1 217.586 | 1 224.665 4 | 1 378.301 |
| 25 | 1 305.289 | 1 313.340 | 1 364.422 2 | 1 498.952 |
| 26 | 1 392.971 | 1 567.526 | 1 526.175 3 | 1 564.604 |
| 27 | 1 658.575 | 1 700.000 | 1 866.358 1 | 2 298.096 |
| 28 | 1 700 | 2 026.563 | 1 700.001 3 | 5 304.414 |
| 序号 | D=10 | D=30 | ||
| IQPSO | DE | IQPSO | DE | |
| 1 | -1 400 | -1 400 | -1 400 | -1 360.54 |
| 2 | 1.289E+6 | 1 281.226 | 1.286E+7 | 1.981E+6 |
| 3 | 2.272E+6 | 1 199.582 | 5.019E+7 | 1.591E+9 |
| 4 | 3.445E+4 | -859.192 | 1.192E+5 | 12 544.49 |
| 5 | -1 000 | -999.999 | -1 000 | -875.731 |
| 6 | -887.677 | -883.220 | -850.223 | -766.068 |
| 7 | -798.826 | -798.671 | -791.202 | -751.271 |
| 8 | -678.875 | -679.607 | -678.608 | -678.993 |
| 9 | -596.532 | -596.370 | -585.435 | -571.621 |
| 10 | -499.148 | -126.906 | -495.840 | 2 070.522 |
| 11 | -393.234 | -335.991 | -379.736 | -32.718 8 |
| 12 | -290.995 | -262.673 | -233.630 | 10.221 97 |
| 13 | -175.726 | -145.015 | -112.452 | 178.707 3 |
| 14 | 15.040 35 | 384.613 0 | 469.649 7 | 2 912.755 |
| 15 | 757.249 5 | 594.665 1 | 6 206.506 | 3 442.421 |
| 16 | 204.992 1 | 200.939 1 | 206.935 2 | 202.664 9 |
| 17 | 317.964 5 | 328.180 7 | 357.369 6 | 582.008 0 |
| 18 | 482.609 7 | 435.885 1 | 688.390 2 | 690.200 7 |
| 19 | 501.064 1 | 920.074 6 | 503.668 2 | 53 154.54 |
| 20 | 604.265 3 | 602.459 4 | 614.972 1 | 614.990 1 |
| 21 | 1 073.501 | 1 136.876 | 1 031.182 | 2 291.273 |
| 22 | 959.052 6 | 1 675.514 | 1 328.177 | 4 876.853 |
| 23 | 1 604.993 | 1 593.678 | 5 872.228 | 6 351.067 |
| 24 | 1 207.599 | 1 238.140 | 1 224.665 4 | 1 380.327 |
| 25 | 1 305.289 | 1 333.463 | 1 364.422 2 | 1 469.512 |
| 26 | 1 392.971 | 1 734.188 | 1 526.175 3 | 1 569.196 |
| 27 | 1 658.575 | 1 773.331 | 1 866.358 1 | 2 520.549 |
| 28 | 1 700 | 2 097.838 | 1 700.001 3 | 4 568.310 |
由表 2可知,就平均优化结果而言,28个测试函数中,当D=10时,IQPSO优于QPSO的有19个,劣于QPSO的有7个,等于普通QPSO的有2个; 当D=30时,IQPSO优于QPSO的增到22个,劣于QPSO的仅有6个. 这表明,IQPSO不仅明显优于QPSO,而且随着维数增加,其优势趋于增大.
由表 3可知,当D=10时,IQPSO优于GSA的有19个,劣于GSA的有7个,等于GSA的有2个; 当D=30时,IQPSO优于GSA的增到20个,劣于GSA的仍为7个,等于GSA的减为1个. 这同样表明,IQPSO不仅明显优于GSA,而且随着维数增加,IQPSO的优势也趋于增大.
由表 4可知,当D=10时,IQPSO优于DE的有18个,劣于DE的有9个,等于DE的有1个; 当D=30时,IQPSO优于DE的增到20个,劣于GSA的减为7个,等于GSA的仍为1个. 这同样表明,IQPSO不仅明显优于DE,而且随着维数增加,IQPSO的优势同样趋于增大.
为进一步考察提出策略的性能,表 5给出了IQPSO和DE在维数D=30时的优化误差对比. 其中,“误差”是指优化结束之后得到的目标值与精确目标值的绝对偏差,而“误差中位值、 误差平均值、 误差标准差”均指30次独立优化得到的30个误差的中位值、 平均值、 标准差.
| 序号 | 误差中位值 | 误差平均值 | 误差方差 | |||
| IQPSO | DE | IQPSO | DE | IQPSO | DE | |
| 1 | 0.000 0 | 19.462 | 0.000 0 | 39.451 | 0.000 0 | 40.969 |
| 2 | 9.1E+6 | 1.8E+6 | 1.0E+7 | 1.9E+6 | 5.6E+6 | 9.5E+5 |
| 3 | 2.3E+7 | 1.5E+9 | 3.9E+7 | 1.5E+9 | 5.1E+7 | 1.1E+9 |
| 4 | 1.2E+5 | 1.1E+4 | 1.2E+5 | 1.3E+4 | 3.6E+4 | 7 383.6 |
| 5 | 1.4E-6 | 101.37 | 2.9E-6 | 124.26 | 3.6E-6 | 89.528 |
| 6 | 39.492 | 129.30 | 44.180 | 133.93 | 26.065 | 35.413 |
| 7 | 7.285 8 | 46.826 | 7.964 7 | 48.728 | 4.626 8 | 21.236 |
| 8 | 21.377 | 21.012 | 21.380 | 21.006 | 0.067 2 | 0.057 8 |
| 9 | 13.698 | 28.102 | 13.984 | 28.378 | 2.927 4 | 2.191 9 |
| 10 | 3.526 7 | 2 567.6 | 3.583 2 | 2 570.5 | 1.718 2 | 7.348 2 |
| 11 | 20.894 | 360.72 | 19.600 | 367.28 | 4.616 3 | 49.177 |
| 12 | 63.180 | 301.93 | 68.322 | 310.22 | 15.760 | 33.041 |
| 13 | 83.956 | 370.00 | 85.145 | 378.70 | 35.151 | 40.107 |
| 14 | 498.76 | 2 906.8 | 581.68 | 3 012.7 | 320.81 | 660.12 |
| 15 | 5 455.1 | 2 983.4 | 5 546.5 | 3 342.4 | 2 480.1 | 1 069.3 |
| 16 | 6.606 9 | 2.696 7 | 6.492 1 | 2.664 9 | 1.082 6 | 0.337 3 |
| 17 | 57.202 | 281.76 | 57.743 | 282.00 | 9.618 9 | 28.305 |
| 18 | 287.80 | 293.66 | 287.04 | 290.20 | 21.128 | 24.847 |
| 19 | 3.756 8 | 5.2E+4 | 3.878 0 | 5.2E+4 | 0.792 3 | 382.10 |
| 20 | 15.000 | 15.000 | 15.000 | 14.990 | 0.000 0 | 0.054 2 |
| 21 | 200.00 | 1 619.1 | 257.68 | 1 591.2 | 78.368 | 95.920 |
| 22 | 487.94 | 4 118.5 | 524.37 | 4 076.8 | 243.27 | 660.41 |
| 23 | 5 328.0 | 5 380.3 | 5 714.9 | 5 451.0 | 2 461.0 | 875.98 |
| 24 | 226.60 | 382.82 | 225.82 | 380.32 | 14.629 | 24.360 |
| 25 | 265.07 | 365.73 | 264.54 | 369.51 | 5.843 3 | 9.709 1 |
| 26 | 321.26 | 371.13 | 322.91 | 369.19 | 10.170 | 16.707 |
| 27 | 597.99 | 1 205.5 | 591.03 | 1 220.5 | 116.85 | 108.72 |
| 28 | 300.00 | 3 138.4 | 339.19 | 3 168.3 | 214.68 | 228.32 |
由表 5可知,就28个测试函数优化误差的中位值、 平均值、 均方差而言,IQPSO的优化结果小于DE结果的函数个数分别为22个、 21个、 20个. 统计结果表明,IQPSO不仅优化能力优于DE,而且具有更好的稳定性.
虽然表 2~5的统计结果对算法性能提供了较为充分的对比,但对于一个好的算法,通常还需要进行算法优越性的显著性检验. 为了确定IQPSO是否获得了在统计意义上比其它算法更优的解,对于28个30维函数,根据IQPSO和QPSO、 GSA、 DE分别优化30次的结果,利用统计阈值α=0.05,进行了秩和检验. 该检验的原假设是: “对于同一函数,IQPSO的优化结果和其它算法的优化结果没有差异”. 检验结果如表 6所示.
| 序号 | IQPSO/QPSO | IQPSO/GSA | IQPSO/DE | |||||||||
| P | R1 | R2 | W | P | R1 | R3 | W | P | R1 | R4 | W | |
| 1 | 2.97E-11 | 465 | 1 365 | + | 2.97E-11 | 465 | 1 365 | + | 2.97E-11 | 465 | 1 365 | + |
| 2 | 3.01E-11 | 465 | 1 365 | + | 4.685E-8 | 545 | 1 285 | + | 3.68E-11 | 1 363 | 467 | - |
| 3 | 3.01E-11 | 465 | 1 365 | + | 8.99E-11 | 476 | 1 354 | + | 6.69E-11 | 473 | 1 357 | + |
| 4 | 3.01E-11 | 1 365 | 465 | - | 3.01E-11 | 1 365 | 465 | - | 3.01E-11 | 1 365 | 465 | - |
| 5 | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + |
| 6 | 6.51E-9 | 522 | 1 308 | + | 8.351E-8 | 552 | 1 278 | + | 1.558E-8 | 532 | 1 298 | + |
| 7 | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + |
| 8 | 3.00E-11 | 1 365 | 465 | - | 3.00E-11 | 1 365 | 465 | - | 3.00E-11 | 1 365 | 465 | - |
| 9 | 3.01E-11 | 465 | 1 365 | + | 4.97E-11 | 470 | 1 360 | + | 3.01E-11 | 465 | 1 365 | + |
| 10 | 1.20E-10 | 479 | 1 351 | + | 3.368E-5 | 634 | 1 196 | + | 3.01E-11 | 465 | 1 365 | + |
| 11 | 3.01E-11 | 465 | 1 365 | + | 5.07E-10 | 494 | 1 336 | + | 3.01E-11 | 465 | 1 365 | + |
| 12 | 3.01E-11 | 465 | 1 365 | + | 2.601E-8 | 538 | 1 292 | + | 3.01E-11 | 465 | 1 365 | + |
| 13 | 5.49E-11 | 471 | 1 359 | + | 9.75E-10 | 501 | 1 329 | + | 3.01E-11 | 465 | 1 365 | + |
| 14 | 3.01E-11 | 465 | 1 365 | + | 2.438E-9 | 511 | 1 319 | + | 3.01E-11 | 465 | 1 365 | + |
| 15 | 0.180 899 | 824 | 1 006 | = | 0.371 077 | 854 | 976 | = | 1.606E-6 | 1 240 | 590 | - |
| 16 | 3.01E-11 | 1 365 | 465 | - | 3.01E-11 | 1 365 | 465 | - | 3.01E-11 | 1 365 | 465 | - |
| 17 | 3.01E-11 | 465 | 1 365 | + | 1.102E-8 | 528 | 1 302 | + | 3.01E-11 | 465 | 1 365 | + |
| 18 | 2.194E-8 | 1 294 | 536 | - | 1.635E-5 | 1 207 | 623 | - | 0.579 294 | 877 | 953 | = |
| 19 | 3.01E-11 | 465 | 1 365 | + | 1.410E-9 | 505 | 1 325 | + | 3.01E-11 | 465 | 1 365 | + |
| 20 | 3.436E-7 | 1 246 | 584 | - | 0.344 558 | 645 | 1 185 | = | 0.151 528 | 491 | 1 339 | = |
| 21 | 6.282E-6 | 609 | 1 221 | + | 0.026 077 | 764 | 1 066 | + | 3.01E-11 | 465 | 1 365 | + |
| 22 | 3.01E-11 | 465 | 1 365 | + | 4.19E-10 | 492 | 1 338 | + | 3.01E-11 | 465 | 1 365 | + |
| 23 | 0.024 154 | 762 | 1 068 | + | 0.033 874 | 771 | 1 059 | + | 0.290 472 | 843 | 987 | = |
| 24 | 1.32E-10 | 480 | 1 350 | + | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + |
| 25 | 1.77E-10 | 483 | 1 347 | + | 5.49E-11 | 471 | 1 359 | + | 3.01E-11 | 465 | 1 365 | + |
| 26 | 8.484E-9 | 1 305 | 525 | - | 5.858E-6 | 608 | 1 222 | + | 4.61E-10 | 493 | 1 337 | + |
| 27 | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + |
| 28 | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + | 3.01E-11 | 465 | 1 365 | + |
| +/=/- | 21/1/7 | 22/2/4 | 20/3/5 | |||||||||
表 6中, P表示原假设为真的概率,R1、 R2、 R3、 R4分别表示IQPSO、 QPSO、 GSA、 DE的秩和,W表示显著性结果: “+”表示原假设被拒绝,IQPSO以95%的显著性水平优于另一算法; “-”表示原假设被拒绝,IQPSO以95%的显著性水平劣于另一算法; “=”表示原假设被接受,两种算法没有统计差别. 表 6最后一行给出了每组算法中IQPSO优于、 等于、 劣于对比算法的函数个数. 显著性测试结果进一步验证了提出算法的优势.
对于上述实验结果,给出如下理论分析: IQPSO的优化能力明显高于QPSO、 GSA、 DE,这是因为在IQPSO中,采用了与QPSO不同的势阱中心设置方法,同时增加了一个新的位置更新式的缘故. 在IQPSO中,每次迭代均从最优解候选集中用轮盘赌策略选择势阱中心,同时提出了一个基于粒子当前位置和平均位置的新的位置更新式,以等概率从两个位置更新式中随机选择其一,这些措施有效增强了种群多样性. 另外,最优解候选集中粒子的个数随迭代步数单调下降,也较好地保持了寻优过程中探索与开发之间的平衡.
5 在量子衍生神经网络中的应用量子衍生神经网络是受量子计算原理的启发,采用量子旋转门和受控非门构造神经元,按量子计算原理构造输入输出关系的新型网络模型. 由于其参数较多,误差曲面极为复杂,普通梯度下降法很容易陷入局部极小. 本文以文[18]中使用的基于序列输入的量子衍生神经网络为例,采用本文提出的IQPSO算法和文[15]中的QPSO算法分别训练,并通过对比训练结果和测试结果验证IQPSO的优势. 选择基于序列输入的量子衍生神经网络,是因为该网络体现了样本的过程式输入,其参数个数远多于其它网络模型,训练难度也大于其它网络模型. 网络模型如图 1所示.

|
| 图 1 基于序列输入的量子衍生神经网络模型 Fig. 1 Sequence input-based quantum-inspired neural networks model |
网络模型中需要优化的参数有: 隐层量子旋转门的旋转角度θij(tr),输出层权值wjk,i=1,2,…,n,j=1,2,…,p,k=1,2,…,m,r=1,2,…,q. 其中n为输入层节点数,p为隐层节点数,m为输出层节点数,q为输入样本的序列长度. 参数总数为D=n×p×q+p×m=(nq+m)p个.
5.2 样本数据本实验使用的样本数据(训练和测试)来源于http://archive.ics.uci.edu/ml/datasets.html中的100种植物叶片数据集. 该数据集包括100种叶片数据,每种16个样本,共1 600个样本. 其中前20类(每类只选1个)如图 2所示. 每个样本包括64个属性值,可用64维向量描述. 为简便,只取前20类样本共320个,其中每类的前12个(共240个)作为训练集,后4个(共80个)作为测试集.

|
| 图 2 部分植物叶片样本图片 Fig. 2 Part of the plant species leaf pictures |
根据样本数据,输入样本为64维行向量; 根据量子衍生神经网络样本的构造方法,将这个64维的行向量变换为8阶方阵. 因此,网络的输入节点n=8,每个样本的序列长度q=8; 为使网络不过于复杂而又有较强逼近能力,隐层节点取p=20; 网络输出为每个样本所属的类别,用1~20的自然数表示,输出层节点数m=1. 因此网络参数共有D=(nq+m)p=(8×8+1)×20=1 300个. 分别采用IQPSO和QPSO优化这些参数. 对于粒子初始化,隐层旋转角度在(-π/2,π/2)内随机取值,输出层权值在(-1,1)内随机取值. 种群规模取100,IQPSO和QPSO的控制参数均取0.5. 算法的终止条件为到达限定迭代步数,且限定迭代步数取500. 目标函数为训练误差.
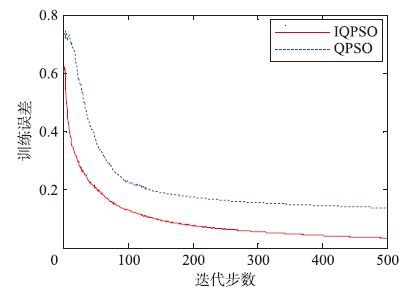
5.4 优化结果对比为体现IQPSO的优势及优化过程的细节,在网络训练过程的每一代,都对测试集进行测试,同时记录当前代训练集样本归一化误差的最大值(E)、 训练集正确分类数(TR)、 测试集正确分类数(TE). 为减小优化结果的随机性,每种算法分别优化50次. 50次优化结束之后,IQPSO与QPSO的优化结果对比如表 7所示. 3个指标50次优化的平均值变化曲线分别如图 3~图 5所示.
|
| 图 3 训练误差对比 Fig. 3 The comparison of the training error |

|
| 图 4 训练正确数对比 Fig. 4 The comparison of the correct number of training results |

|
| 图 5 测试正确数对比 Fig. 5 The comparison of the correct number of testing results |
从表 7可知,IQPSO 50次优化的平均结果,训练误差比QPSO小0.1,训练集正确数比QPSO多24个,测试集正确数比QPSO多10个. 对于优化过程的细节,从图 3~5可知,IQPSO的3项指标自始至终一直优于QPSO. 实验结果表明,对于含大量参数的神经网络训练这类高维优化问题,IQPSO同样优于QPSO.
| 序号 | IQPSO | QPSO | ||||
| E | TR | TE | E | TR | TE | |
| 1 | 0.026 8 | 237 | 60 | 0.105 2 | 231 | 54 |
| 2 | 0.029 4 | 239 | 61 | 0.039 8 | 229 | 56 |
| 3 | 0.023 9 | 240 | 62 | 0.054 1 | 230 | 54 |
| 4 | 0.027 2 | 239 | 64 | 0.099 8 | 231 | 58 |
| 5 | 0.026 3 | 240 | 64 | 0.054 1 | 221 | 58 |
| 6 | 0.025 5 | 240 | 64 | 0.087 1 | 221 | 56 |
| 7 | 0.037 4 | 238 | 62 | 0.154 7 | 222 | 53 |
| 8 | 0.042 7 | 238 | 61 | 0.045 7 | 234 | 55 |
| 9 | 0.031 0 | 238 | 66 | 0.042 3 | 229 | 56 |
| 10 | 0.027 3 | 239 | 62 | 0.105 2 | 203 | 52 |
| 11 | 0.037 8 | 239 | 64 | 0.104 8 | 225 | 56 |
| 12 | 0.035 7 | 238 | 59 | 0.155 1 | 233 | 52 |
| 13 | 0.029 9 | 239 | 66 | 0.103 6 | 231 | 54 |
| 14 | 0.031 7 | 238 | 65 | 0.046 1 | 233 | 54 |
| 15 | 0.028 8 | 239 | 63 | 0.045 7 | 233 | 54 |
| 16 | 0.038 6 | 238 | 60 | 0.043 4 | 227 | 57 |
| 17 | 0.031 4 | 238 | 60 | 0.052 2 | 228 | 47 |
| 18 | 0.044 0 | 238 | 65 | 0.153 0 | 223 | 57 |
| 19 | 0.036 4 | 238 | 67 | 0.156 4 | 228 | 56 |
| 20 | 0.057 0 | 237 | 58 | 0.047 5 | 231 | 55 |
| 21 | 0.036 6 | 239 | 64 | 0.046 9 | 232 | 57 |
| 22 | 0.035 2 | 237 | 61 | 0.198 6 | 223 | 55 |
| 23 | 0.030 0 | 239 | 67 | 0.105 2 | 230 | 51 |
| 24 | 0.022 1 | 240 | 65 | 1.000 0 | 12 | 4 |
| 25 | 0.040 9 | 239 | 63 | 0.051 6 | 226 | 55 |
| 26 | 0.058 7 | 235 | 60 | 0.156 7 | 224 | 52 |
| 27 | 0.026 0 | 240 | 62 | 0.055 9 | 234 | 54 |
| 28 | 0.029 9 | 239 | 62 | 0.051 4 | 229 | 58 |
| 29 | 0.038 4 | 239 | 67 | 0.052 1 | 226 | 56 |
| 30 | 0.042 2 | 238 | 58 | 0.102 9 | 225 | 58 |
| 31 | 0.035 1 | 238 | 60 | 0.041 3 | 231 | 52 |
| 32 | 0.034 1 | 239 | 60 | 0.068 4 | 224 | 50 |
| 33 | 0.035 5 | 238 | 61 | 0.104 5 | 230 | 56 |
| 34 | 0.031 9 | 239 | 61 | 0.104 5 | 226 | 56 |
| 35 | 0.033 4 | 238 | 63 | 0.078 3 | 221 | 49 |
| 36 | 0.019 6 | 240 | 62 | 0.068 7 | 223 | 48 |
| 37 | 0.027 9 | 238 | 62 | 0.056 6 | 236 | 61 |
| 38 | 0.037 7 | 238 | 60 | 0.059 5 | 227 | 57 |
| 39 | 0.037 7 | 238 | 60 | 0.060 2 | 230 | 52 |
| 40 | 0.034 4 | 238 | 61 | 0.078 0 | 214 | 57 |
| 41 | 0.027 2 | 239 | 62 | 0.096 5 | 230 | 58 |
| 42 | 0.019 2 | 240 | 60 | 0.050 9 | 231 | 54 |
| 43 | 0.032 0 | 237 | 61 | 1.000 0 | 12 | 16 |
| 44 | 0.034 8 | 238 | 62 | 0.105 0 | 230 | 56 |
| 45 | 0.029 3 | 239 | 64 | 0.105 2 | 194 | 49 |
| 46 | 0.031 9 | 238 | 58 | 0.066 3 | 230 | 60 |
| 47 | 0.030 5 | 238 | 62 | 0.048 5 | 233 | 54 |
| 48 | 0.030 7 | 238 | 62 | 0.105 1 | 233 | 54 |
| 49 | 0.026 2 | 240 | 60 | 1.000 0 | 12 | 4 |
| 50 | 0.026 3 | 240 | 63 | 0.040 8 | 236 | 63 |
| 平均 | 0.032 9 | 238 | 62 | 0.137 1 | 214 | 52 |
提出了一种改进的量子行为粒子群优化算法. 改进算法基于最优解候选集和轮盘赌策略,重新构造了势阱中心的设计方法. 采用不同维数的标准函数极值优化和更为复杂的神经网络权值优化进行仿真验证,实验结果均表明改进算法优于原算法,从而验证了改进措施的有效性. 探索该算法在多目标约束优化问题中的应用将是下一步研究的方向.
| [1] | Sun J, Xu W B, Feng B. A global search strategy of quantum-behaved particle swarm optimization[C]//Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems. Piscataway, NJ, USA: IEEE, 2004: 111-116. |
| [2] | Sun J, Wu X J, Fang W. Multiple sequence alignment using the hidden Markov model trained by an improved quantum-behaved particle swarm optimization[J]. Information Sciences, 2012, 182(1): 93-114. |
| [3] | Sun J, Xu W B, Feng B. Adaptive parameter control for quantum-behaved particle swarm optimization on individual level[C]//2005 IEEE International Conference on System, Man, and Cybernetics. Piscataway, NJ, USA: IEEE, 2005: 3049-3054. |
| [4] | Sun J, Wua X J, Vasile P. Convergence analysis and improvements of quantum-behaved particle swarm optimization[J]. Information Sciences, 2012, 193(3): 81-103. |
| [5] | Coelho L S. Novel Gaussian quantum-behaved particle swarm optimizer applied to electromagnetic design[J]. IET Science, Measurement & Technology, 2007, 1(5): 290-294. |
| [6] | Coelho L S, Nedjah N, Mourelle L M. Gaussian quantum-behaved particle swarm optimization applied to fuzzy PID controller design[J]. Studies in Computational Intelligence, 2008, 121(6): 1-15. |
| [7] | Coelho L S. Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems[J]. Expert Systems with Applications, 2010, 37(2): 1676-1683. |
| [8] | Jun S, Wei F, Vasile P. Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point[J]. Applied Mathematics and Computation, 2011, 218(9): 3763-3775. |
| [9] | Jau Y M, Su K L, Wub C J. Modified quantum-behaved particle swarm optimization for parameters estimation of generalized nonlinear multi-regressions model based on Choquet integral with outliers[J]. Applied Mathematics and Computation, 2013, 221(11): 282-295. |
| [10] | Mostafa J, Reza S, Morteza G. Quantum behaved particle swarm optimization with differential mutation operator applied to WWER-1000 in-core fuel management optimization[J]. Annals of Nuclear Energy, 2013, 54(1): 134-140. |
| [11] | Sun J, Fang W, Wang D J. Solving the economic dispatch problem with a modified quantum-behaved particle swarm optimization method[J]. Energy Conversion and Management, 2009, 50(8): 2967-2975. |
| [12] | Viviana C M, Anderson R K, Fabio A G. A chaotic quantum-behaved particle swarm approach applied to optimization of heat exchangers[J]. Applied Thermal Engineering, 2012, 42(5): 119-128. |
| [13] | Liu F, Duan H b, Deng Y M. A chaotic quantum-behaved particle swarm optimization based on lateral inhibition for image matching[J]. Optik, 2012, 123(2): 1955-1960. |
| [14] | Giuliano B, Giulio C, Giuliano S. Principles of quantum computation and information, Volume I: Basic concepts[M]. Singapore: World Scientific, 2004: 100-112. |
| [15] | 方伟, 孙俊, 谢振平, 等. 量子粒子群优化算法的收敛性分析及控制参数研究[J]. 物理学报, 2010, 59(6): 3686-3694. Fang W, Sun J, Xie Z P, et al. Convergence analysis of quantum-behaved particle swarm optimization algorithm and study on its control parameter[J]. Acta Physica Sinica, 2010, 59(6): 3686-3694. |
| [16] | Liang J J, Qu B Y, Sugamthan P N, et al. Problems definition and evaluation criteria for the CEC 2013 special session on real-parameter optimization[R]. Singapore: Nanyang Technological University, 2013. |
| [17] | Esmat R, Hossein N, Saeid S. GSA: A gravitational search algorithm[J]. Information Sciences, 2009, 179(6): 2232-2248. |
| [18] | 肖红, 李盼池. 量子衍生神经网络及其在图像恢复中的应用[J]. 智能系统学报, 2013, 8(6): 537-542. Xiao H, Li P C. Quantum-derived neural network model and its application to image restoration[J]. CAAI Transactions on Intelligent Systems, 2013, 8(6): 537-542. |



