2. 吉林大学控制科学与工程系,吉林 长春 130022
2. Department of Control Science and Engineering, Jinlin University, Changchun 130022, China
随着汽车保有量的逐年增加,汽车的操纵稳定性及主动安全性问题受到了广泛的关注. 汽车的主动安全性控制系统可以有效地提高汽车操纵稳定性,从而可以减少交通事故的发生. 而汽车主动安全性系统的各种控制逻辑得以有效实施的前提是准确获得车辆的行驶状态[1, 2]. 其中轮胎作为车辆与路面连接的唯一部件,其受力情况对车辆的动态性能有很大影响. 然而在量产车中,汽车轮胎力是无法由车载传感器直接测量得到的,因此如何准确地获得汽车轮胎力成为车辆稳定性控制的关键.
在早期的研究中,轮胎力通常是由实验性的模型推导出来的[3, 4]. 近些年来,随着传感器技术的迅速发展,一些研究人员尝试通过直接或间接测量的办法来获得轮胎力的值[5],然而这种通过测量来获得汽车轮胎力的方法虽然比较精确,但是实现复杂、 成本高,无法普及. 由于基于测量的方法存在严重的缺点,在实际中难以推广,因此人们逐渐倾向于利用车辆已经装备的传感器所测量得到的车辆状态信息,通过估计方法来获得纵向及侧向轮胎力的值.
目前,对于轮胎力估计的研究已经取得了一些成果. 在文[6, 7]中,采用了神经网络的方法对轮胎力的不确定性进行补偿,从而得到了较好的轮胎力估计结果. 但是,采用神经网络的方法很难对映射关系进行机理性解释,另外又由于该方法有收敛性差和数值稳定性差的特点,因此很难将其应用到实车上. 文[8, 9, 10]通过测量车辆状态信息,分别使用了扩展卡尔曼滤波、 无迹卡尔曼滤波和随机卡尔曼滤波的方法来估计汽车轮胎力. 这种方法的好处是它将所有的轮胎力动态特性假设为由白噪声驱动的随机过程,而不需要轮胎/路面摩擦系数的先验知识和轮胎力模型. 但此方法只适用于非线性不是很强的系统,当车辆在极限工况行驶时,卡尔曼滤波器可能极不稳定,甚至发散,并且估计求解过程中较大的计算量也增加了估计算法的实现难度. 文[11]应用自适应观测器进行轮胎力的估计,该观测器考虑了道路摩擦力的变化. 文[12]提出了鲁棒性轮胎力估计算法,该算法能够辨识各个车轮的纵向和侧向轮胎力. 文[13, 14]基于扰动输入观测器理论及单轮滚动动力学模型设计了非线性观测器来得到每个车轮的纵向轮胎力的估计值.
近年来,基于滑模观测器的估计算法得到迅速发展,并广泛应用于非线性车辆系统中. 文[15]基于7自由度车辆模型设计了滑模观测器,并获得了较为准确的轮胎力估计值. 文[16]基于2自由度车辆动力学模型,并利用车辆已配备的传感器测量信息,设计了一种基于滑模技术的轮胎力观测器. 文[17]设计了一种高阶滑模观测器对重型车辆进行鲁棒性轮胎力估计. 上述研究表明,滑模观测器方法在轮胎力估计方面具有较高的准确度,具有对参数变化及外部扰动不敏感、 鲁棒性强、 动态响应快等特点. 特别在车辆的实际运行中,它具有计算量小和实时性好的特点.
由于滑模观测器具有上述优点,本文提出了一种基于滑模观测器理论的车辆轮胎力估计方法,分别采用了车辆单轮滚动动力学模型及2自由度模型对纵向和侧向轮胎力进行了估计,并在选取了直线加速工况、 常规双移线工况和低附着双移线工况对观测器的估计效果进行了验证.
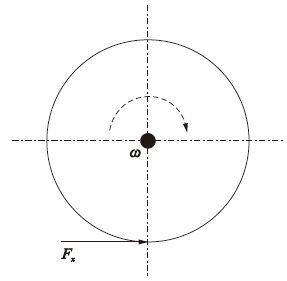
2 车辆动力学建模 2.1 纵向轮胎力对纵向轮胎力进行估计时,本文采用了车辆单轮滚动动力学模型,如图 1所示.
|
| 图 1 单轮滚动动力学模型 Fig. 1 Single wheel dynamic model |
由图 1可以得到,每个车轮的动力学方程如式(1)所示:
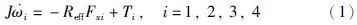
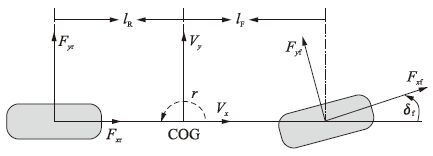
对侧向轮胎力进行估计时,为了方便研究,本文将整车模型简化为只包含侧向运动和横摆运动的2自由度模型. 在车辆上建立坐标系,原点位于汽车的质心,车辆前进的方向为x轴正方向,水平向左为y轴正方向,z轴正方向由右手螺旋定则确定,如图 2所示.
|
| 图 2 2自由度车辆模型 Fig. 2 2-DOF vehicle dynamic model |
由牛顿第二定律及转矩平衡方程可知,在车辆坐标系下,车辆沿y轴的侧向运动方程和绕z轴的转矩平衡方程可以用式(2)表示:
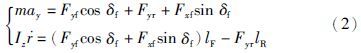
为了方便对本文的估计问题进行介绍,根据文[18],首先将能够通过车辆传感器直接测量的参数作如下说明:
(1) 4个车轮的驱动力矩Ti(i=1,2,3,4)虽然不可直接测量,但可以通过车辆其它可测量信息(发动机力矩Te、 发动机转速ωe、 制动轮缸压力pt)通过计算得到,因此可以将其视作可直接测量信息;
(2) 车辆方向盘的转角信号可通过光电编码器测量得到,进而能够计算得到车辆的前轮转角δf;
(3) 4个车轮的转动角速度ωi(i=1,2,3,4)可通过轮速传感器测量得到;
(4) 车辆侧向加速度ay可通过加速度传感器测量得到;
(5) 车辆横摆角速度r可通过陀螺仪测量得到.
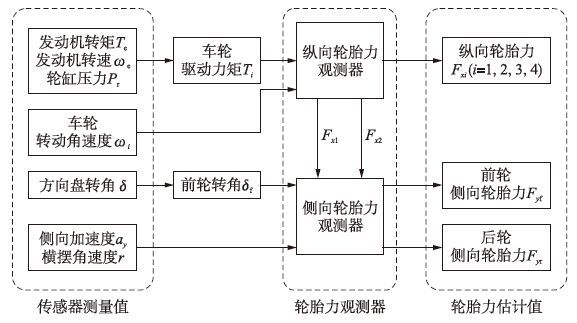
为方便研究,本文假设车辆在平直的道路上行驶,即忽略车辆的侧倾和俯仰运动,图 3为车辆轮胎力估计的整体方案.
|
| 图 3 轮胎力观测器结构 Fig. 3 Structure of the tire force observer |
在图 3中,车轮驱动力矩Ti及车轮转动角速度ωi作为纵向轮胎力观测器的测量输入值,其中车轮驱动力矩Ti由发动机力矩Te、 发动机转速ωe、 制动轮缸压力pt计算得到,该观测器的输出值为4个轮的纵向轮胎力Fxi(i=1,2,3,4).
在侧向轮胎力估计中,以前轮转角δf、 侧向加速度ai及横摆角速度r为测量输入值,其中前轮转角δf可以由方向盘转角δ通过关系式δ=δf/Isw计算得到,Isw为转向传动比. 并将已估计出的纵向轮胎力Fx1、 Fx2作为侧向轮胎力观测器输入信号,形成级联估计器,因此纵向轮胎力的估计准确性在一定程度上也影响了侧向轮胎力的估计准确性. 该观测器的输出值分别为车辆前、 后轴侧向轮胎力Fyf和Fyr.
3.2 滑模观测器设计滑模控制是自动控制系统的一种设计方法,对于系统参数不确定性和外部扰动具有强鲁棒性[19],因此在许多领域得到了推广和应用. 滑模控制系统的所有分析、 设计及实现都以状态量的可测性为基础,但在实际中,很多控制系统的状态量并非全部可直接测量. 而基于滑模控制理论设计的状态观测器不但可以用于估计控制系统的状态,而且滑模观测器同样具有滑模控制鲁棒性,是一种性能优良的观测器,具有广阔的应用前景. 下面给出滑模观测器的具体设计内容.
考虑到特殊的1阶系统:

根据滑模观测器理论,在这里定义系统误差为$\tilde x$=x-$\hat x$,本文选取滑模面为系统误差,即S=$\tilde x$,并选取李亚普诺夫函数:

对式(4)求导,可得

根据状态观测器理论,将式(3)构造成如下形式,其中L是观测器增益:
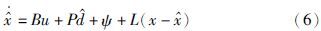
将式(3a)和式(6)代入式(5),可以得到:
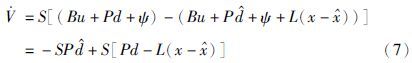
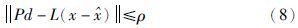
在上述假设中,如果d满足有界条件,则只要ρ取足够大的值,假设是可以成立的. 将式(8)代入到式(7),可以得到:
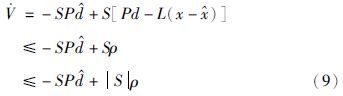
此时若取$\hat d$=P-1ρsgn S,其中sgn S是符号函数,可表示为
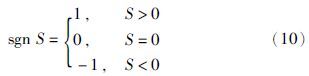
进而可以将式(9)表示为
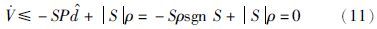
由上述推导过程,本文设计的滑膜观测器形式如下:
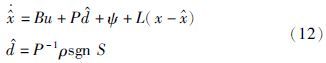
结合式(3)和式(12)进一步将系统误差导数表示为
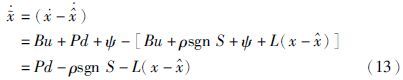
当时间为t1、 系统达到稳定时,可得$\dot{\tilde{x}}$=0,因此:
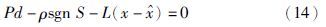
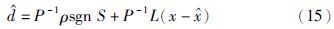
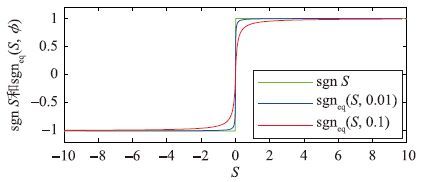
由于时间滞后、 空间滞后及系统惯性等影响,滑模系统容易出现抖振现象[20]. 这将增大估计误差,从而影响估计结果. 为了消除抖振的影响,本文采用饱和函数(16)代替符号函数sgn S[21]:
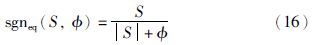
|
| 图 4 符号函数 Fig. 4 Sign function |
由图 4可以看出,当使用符号函数sgn S时,一但出现估计误差并且估计误差符号改变,就会导致函数在±1之间来回切换,从而容易引入较快的抖振频率. 而采用饱和函数sgneq(S,φ),可以使切换面变为一个连续的函数,从而起到抑制抖振的效果.
3.2.1 纵向轮胎力估计将车轮动力学平衡方程(1)化为形如式(3)的形式:
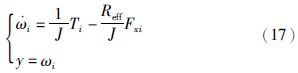
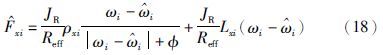
考虑到式(2)中所示的车辆2自由度平衡方程,将其中的前轮侧向轮胎力Fyf和后轮侧向轮胎力Fyr去耦合:
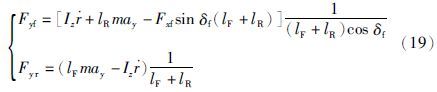
对于前轮侧向轮胎力Fyf,将式(19)化为形如式(3)的形式:
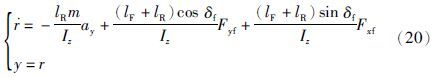
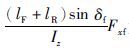 为干扰项,由上述推导过程可知,干扰项不影响最终所设计的观测器形式.
为干扰项,由上述推导过程可知,干扰项不影响最终所设计的观测器形式.
根据式(15)中所设计的滑模观测器形式,本文设计的前轮侧向轮胎力滑模观测器形式如下:
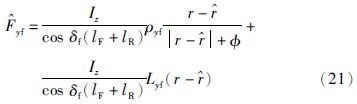
同理可以设计后轮侧向轮胎力滑膜观测器形式:
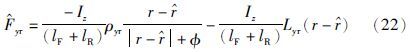
为验证本文设计的轮胎力滑模观测器的估计效果,本节将分别给出车辆在3种典型工况下运行的仿真结果. 其中直线加速工况用来验证纵向轮胎力的估计效果,双移线工况则分别验证了纵向轮胎力和侧向轮胎力的估计效果. 实验时,使用了高保真车辆动力学软件veDYNA的整车模型作为仿真车辆,具体参数如表 1所示. 在不同运行工况下,通过调节纵向及侧向轮胎力观测器中的滑模增益ρ=18及反馈增益L=200,并且令φ=0.01时轮胎力估计值达到最佳. 此外为了对比本文所设计的轮胎力滑模观测器与常用的扩展卡尔曼滤波器方法的估计性能,同时将EKF方法应用于本文的车辆模型[22],选取最佳的初值状态,并给出在相同运行工况下,二者估计效果的对比分析.
| 符号 | 单位 | 值 |
| m | kg | 1 296 |
| lF | m | 1.25 |
| lR | m | 1.32 |
| J | kg·m2 | 0.8 |
| Iz | kg·m2 | 1 750 |
| Reff | m | 0.288 |
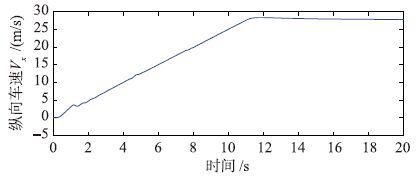
为验证纵向轮胎力的估计效果,首先让车辆在纯纵向工况下运行. 在路面摩擦系数μ=0.8的道路上,车辆由静止开始加速到100 km/h,之后保持匀速直线运动,图 5为车辆纵向速度变化过程.
|
| 图 5 纵向车速 Fig. 5 Longitudinal vehicle velocity |
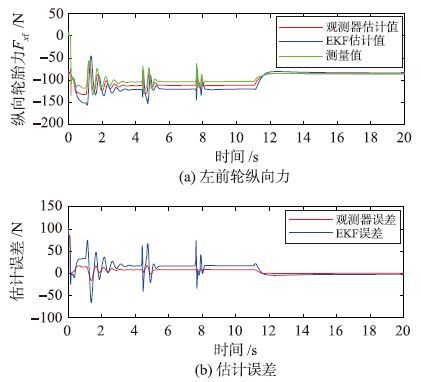
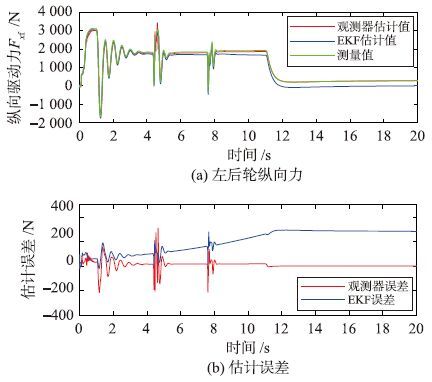
考虑到车辆系统的对称性,只给出左侧纵向轮胎力的估计结果. 图 6和图 7分别为该工况下,左前轮及左后轮纵向轮胎力估计对比曲线及其估计误差. 在估计对比曲线图中,3条曲线分别代表纵向轮胎力的滑模观测器估计值、 EKF滤波器估计值及实际测量值.
|
| 图 6 直线加速实验左前轮纵向轮胎力仿真结果 Fig. 6 Simulation results of the left-front longitudinal tire force from the linear acceleration operation |
|
| 图 7 直线加速实验左后轮纵向轮胎力仿真结果 Fig. 7 Simulation results of the left-rear longitudinal tire force from the linear acceleration operation |
从仿真结果可以看出,通过两种方法得到的纵向轮胎力估计值都有一定的误差,特别是当时间在4 s和8 s附近时,仿真曲线产生了明显的振动,这是由于行驶换挡过程引起的. 而从二者的估计误差中可以看出,滑模观测器估计器的估计误差要小于EKF滤波器的估计误差,即基于滑模观测器的方法要比基于EKF方法的估计精度高. 而在设计和实现的难易程度上,滑模观测器的设计和应用比较简单,并且可以直接通过调节滑模增益和反馈增益来调整动态性能,并且不需要相关模型的测量噪声的统计特性.
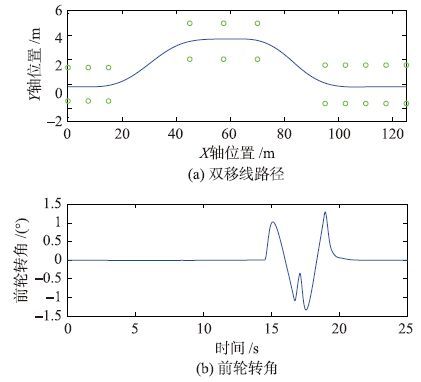
4.2 常规双移线实验考虑到车辆行驶的一种典型工况,激发轮胎的侧向特性: 在路面摩擦系数μ=0.8的道路上,车辆由静止开始加速,当车辆速度加速到80 km/h时,进行双移线操作,之后保持匀速直线运动. 图 8为仿真行驶路径及方向盘转角的大小.
|
| 图 8 双移线运行工况 Fig. 8 Double lane operation |
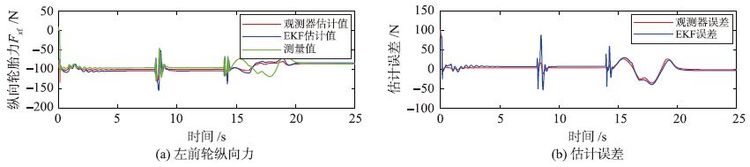
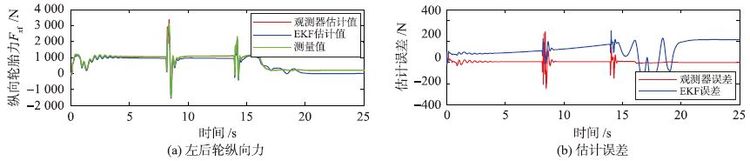
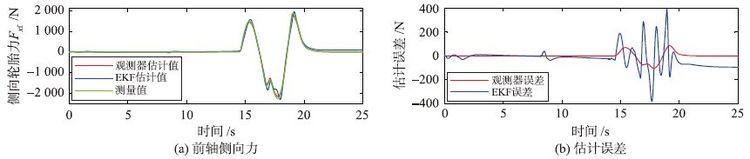
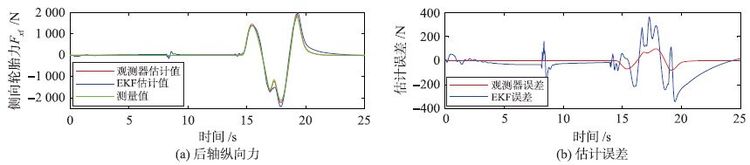
在此工况下分别对纵向及侧向轮胎力的估计效果进行验证,实验得到的结果如图 9~12所示. 其中图 9和图 10分别为左前轮及左后轮纵向轮胎力估计对比曲线及其估计误差,图 11和图 12分别为前、 后轴侧向轮胎力估计对比曲线及其估计误差.
|
| 图 9 常规双移线工况左前轮纵向轮胎力仿真结果 Fig. 9 Simulation results of the left-front longitudinal tire force from the conventional double lane operation |
|
| 图 10 常规双移线工况左后轮纵向轮胎力仿真结果 Fig. 10 Simulation results of the left-rear longitudinal tire force from the conventional double lane operation |
|
| 图 11 常规双移线工况前轮侧向轮胎力仿真结果 Fig. 11 Simulation results of the front lateral tire force from the conventional double lane operation |
|
| 图 12 常规双移线工况后轮侧向轮胎力仿真结果 Fig. 12 Simulation results of the rear lateral tire force from the conventional double lane operation |
从仿真结果可以看出,对于纵向轮胎力的估计效果与直线加速工况类似,较大的误差仍出现在车辆行驶的换挡时刻,并且基于滑模观测器的估计方法误差仍要小于基于EKF滤波器方法的误差. 对于侧向轮胎的估计效果,可以看出较大的误差出现在双移线操作阶段,这是由于车辆进行大幅度操纵时侧向轮胎力接近饱和,此时轮胎已经进入强非线性工作区. 而对比两种方法的估计效果,基于滑模观测器的方法同样要比基于EKF方法的估计误差小得多.
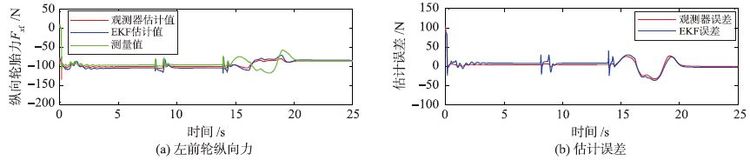
4.3 低附着双移线实验为进一步验证本文所设计的轮胎力滑模观测器在极限工况下的有效性,下面选取了低附着双移线工况进行了进一步实验. 具体工况设置为: 在路面摩擦系数μ=0.4的道路上,车辆由静止开始加速,当车辆速度加速到80 km/h时,进行双移线操作,之后保持匀速直线运动. 在此工况下的估计结果如图 13~16所示.
|
| 图 13 低附着双移线工况左前轮纵向轮胎力仿真结果 Fig. 13 Simulation results of the left-front longitudinal tire forcefrom the low adhesion double lane operation |
|
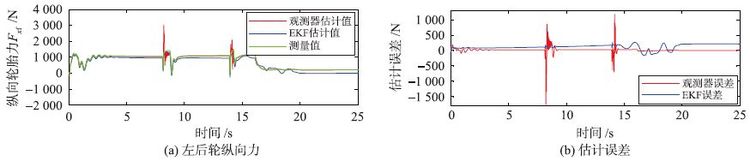
| 图 14 低附着双移线工况左后轮纵向轮胎力仿真结果 Fig. 14 Simulation results of the left-rear longitudinal tire force from the low adhesion double lane operation |
|
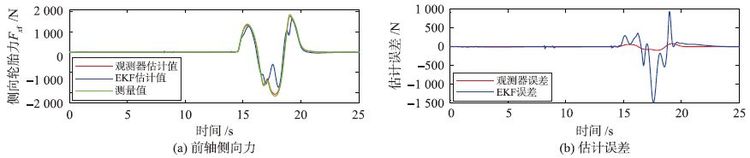
| 图 15 低附着双移线工况前轮侧向轮胎力仿真结果 Fig. 15 Simulation results of the frontlateral tire force from thelow adhesion double lane operation |
|
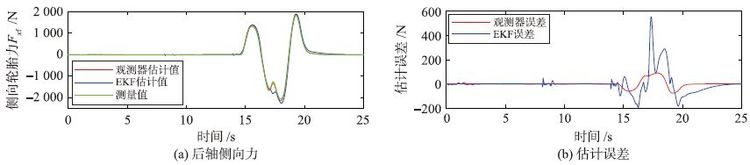
| 图 16 低附着双移线工况后轮侧向轮胎力仿真结果 Fig. 16 Simulation results of the rearlateral tire force from thelow adhesion double lane operation |
从仿真结果可以看出,在此工况下,滑模观测器对于后轮纵向力的估计结果在换挡时刻产生了明显的误差,这也是滑模观测器在汽车换挡时刻容易产生较大抖振的一个缺点,但是对于前轮纵向力及前、 后轴侧向力的估计结果仍然可以保持较好的估计精度. 而此时,基于EKF滤波器方法的估计结果则产生了较大的误差,这是由于此时汽车已经进入了强非线性工作区域,EKF滤波器开始不稳定.
5 结论本文采用滑模观测器的方法分别对每个车轮的纵向轮胎力及前、 后轴侧向轮胎力进行了估计. 其中,采用了在实际中相对容易测量得到的车辆状态信息,包括车轮转动角速度、 驱动力矩、 前轮转角、 侧向加速度及横摆角速度作为观测器的输入. 仿真时,通过3种不同工况下的实验与EKF滤波器方法的估计效果进行了对比分析,得出了基于滑模观测器的轮胎力估计方法更加灵活、 计算量小,更能满足实时性要求,适合实车使用的结论. 但同时,本文所设计的滑模观测器也存在一定的问题,如后轮纵向轮胎力的估计结果在换挡时刻容易产生较大的误差,这也需要在今后的研究中进行进一步改进. 而本文所涉及的滑模增益ρ及反馈增益L是基于大量实验所获得的经验值,虽然具有一定的鲁棒性,但还不能应用于全部的工况,因此在实际应用中还需要对其进行实时调节. 在今后的研究中,可以考虑采用参数自适应的方法来对滑模观测器参数进行实时调整.
| [1] | Kang M, Li L, Li H, et al. Coordinated vehicle traction control based on engine torque and brake pressure under complicated road conditions[J]. Vehicle System Dynamic, 2012, 50(9): 1473-1494. |
| [2] | Cho W, Choi J, Kim C, et al. Unified chassis control for the improvement of agility, maneuverability, and lateral stability[J]. IEEE Transactions on Vehiclar Technology, 2012, 61(3): 1008-1020. |
| [3] | Gipser M, Hofer R, Lugner P. Dynamic tyre forces response to road unevenness[J]. Vehicle System Dynamics, 2007, 27(1): 94-108. |
| [4] | Delanne Y, Beurier G, M'Sirdi N K. Evaluation of tire/road friction performance models from on-site measurements[C]//Proceedings of the Fourth International Symposium on pavement Surface Characteristics on Roads and Airfields. 2000: 423-431. |
| [5] | Madhusudhanan A K, Corno M, Holweg E. Lateral vehicle dynamics control based on tyre utilization coefficients and tyre force measurements[C]//2013 IEEE 52nd Annual Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2013: 2816-2821. |
| [6] | Matuško J, Petrović I and Perić N. Neural network based tire/road friction force estimation[J]. Engineering Applications of Artificial Intelligence, 2008, 21(3): 442-456. |
| [7] | Boada M J L, Boada B L, Garcia-Pozuelo D, et al. Application of neural networks for estimation of tyre/road Forces[C]//ASME 2009 International Mechanical Engineering Congress and Exposition. New York, USA: American Society of Mechanical Engineers. 2009: 427-433. |
| [8] | Louis L, Schramm D. Nonlinear state estimation of tire-road contact forces using a 14 DoF vehicle model[J]. Applied Mechanicsand Materials, 2012, 165: 155-159. |
| [9] | Nada E S, Ahmed A, Abd-Alla M. Modified dual unscented Kalman filter approach for measuring vehicle states and vehicle parameters[J]. International Journal of Engineering Research Technology (IJERT), 2014, 3(8): 1423-1430. |
| [10] | Cho W, Yoon J, Yim S, et al. Estimation of tire forces for application to vehicle stability control[J]. IEEE Transactions on Vehiclar Technology, 2010, 59(2): 638-649. |
| [11] | Baffet G, Charara A, Member, et al. An observer of tire-road forces and friction for active security vehicle systems[J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(6): 651-661. |
| [12] | Hsiao T, Liu N C, Chen S Y. Robust estimation of the friction forces generated by each tire of a vehicle[C]//2011American Control Conference (ACC). Piscataway, NJ, USA: IEEE, 2011: 5261-5266. |
| [13] | Wang R R, Wang J M. Tire-road friction coefficient and tire cornering stiffness estimation based on longitudinal tire force difference generation[J]. Control Engineering Practice, 2013, 21(1): 65-75. |
| [14] | 杨斯琦, 解小华, 陈虹. 一种新型的轮胎力级联估计方法[J]. 信息与控制, 2015, 44(2): 203-214. Yang S Q, Xie X H, Chen H. Vehicle tire forces estimation using a novel cascade method[J]. Information and Control, 2015, 44(2): 203-214. |
| [15] | Haiyan Z, Hong C, Haitao S, et al. Estimation for tyre force based on sliding mode observer[C]//27th Chinese Control Conference. Piscataway, NJ, USA: IEEE, 2008: 691-695. |
| [16] | Slimi H, Arioui H, Mammar S. Motorcycle lateral dynamic estimation and lateral tire-road forces reconstruction using sliding mode observer[C]//16th International IEEE Conference on Intelligent Transportation Systems. Piscataway, NJ, USA: IEEE, 2013: 584-589. |
| [17] | Khemoudj O, Imine H, Djemai M. Variable gain sliding mode observer for heavy duty vehicle tyre forces estimation[C]//Proceedings of the 11th International Workshop on Variable Structure Systems. 2010: 522-527. |
| [18] | 张立达. 用于ESP系统的汽车状态软测量算法开发[D]. 长春: 吉林大学, 2009. Zhang L D. Research on Soft-Sensing Algorithm of Vehicle State for ESP[D]. Changchun: Jilin University, 2009. |
| [19] | Ma L, Wang Z, Niu Y, et al. Sliding mode control for a class of nonlinear discrete-time networked systems with multiple stochastic communication delays[J]. International Journal of Systems Science, 2011, 42(4): 661-672. |
| [20] | 李琳. 滑模变结构控制系统抖振抑制方法的研究[D]. 大连: 大连理工大学, 2007. Li L. A study of chattering elimination in sliding mode control system[D]. Dalian: Dalian University of Technology, 2007. |
| [21] | 赵林辉, 刘志远, 陈虹. 一种车辆状态滑模观测器的设计方法[J]. 电机与控制学报, 2009, 13(4): 565-570. Zhao L H, Liu Z Y, Chen H. Design method of sliding model observer for vehicle state[J]. Electric Machines and Control, 2009, 13(4): 565-570. |
| [22] | 苏海涛. 汽车非线性轮胎力的估计方法研究[D]. 长春: 吉林大学, 2007. Su H T. Research on the methods of vehicle nonlinear tyre forces estimation[D]. Changchun: Jilin University, 2007. |



