2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
遥操作已经成为机器人系统中广泛采用的控制策略. 遥操作系统的原理图如图 1所示. 遥操作的独特性在于主端操控器和遥机器人之间存在通讯环节,其常常具有窄带宽和低通讯频率的特性. 有时,通讯频率可以低至4 Hz. 另外,在很多新兴的机器人应用领域,如空间机器人、 服务机器人和医疗机器人等,轻型机器人正在被越来越广泛地使用. 由于其轻型的结构,轻型机器人比传统的刚性机器人具有小得多的惯性,这使得它们的灵活性更强. 但这也使得机器人结构的柔性显著增加. 轻型机器人的振动是一个突出的问题,其中振动辨识是一个非常重要的方面.

|
| 图 1 遥操作系统的原理图 Fig. 1 The schematic diagram of the telemanipulation system |
当考虑遥操作系统中轻型机器人结构振动的辨识问题时,传统的振动辨识方法将会遭遇瓶颈. 传统方法基于奈奎斯特采样定理,要求采样频率必须高于被辨识振动信号最高频率的2倍. 根据奈奎斯特采样定理对振动信号采样将会产生大量的采样数据. 如果尝试将采样数据从远端发送到本地,就不得不使用很低的系统通讯频率进行发送,致使每次发送都要包含很大的数据量. 遥操作系统通讯环节的窄带宽通常无法胜任这样的发送任务. 所以,减小要发送的数据量是非常必要的. 在这种情况下,需要研究如何从不满足奈奎斯特采样定理的数据中恢复振动信号,即机械结构振动的欠采样辨识问题.
在通信工程领域,对于信号的欠采样辨识方法已经有了很多研究工作. Shi等[1]针对超宽带模数转换提出一种平行采样策略,应用这种策略可以使采样率降至奈奎斯特采样率的1/m,其中m是平行通道数. Maroosi等[2]针对欠采样实正弦波形的频率测定问题提出了一种新方法,这种方法相比于欠采样正弦复波形的频率测定需要更低的硬件开销. 王玉兰等[3]提出一种采用互相关算法的欠采样频率测量方法,能够实现对高频信号的频率的精密测量. 黄佑勇等[4]、 王洪洋等[5]基于ESPRIT方法,对宽频段信号进行欠采样频率估计,采用了增加信号延时通道的方法解决欠采样导致的频率混叠问题. 还有很多与欠采样信号辨识相关的工作,这里不再列举. 但是,欠采样辨识方法被用于辨识机械结构的振动仍然很少见到. 李孟麟等[6]、 欧阳涛等[7]基于叶尖定时测振原理,研究了旋转机械叶片振动的欠采样观测,他们分别利用插值法和倍频遍历法对叶片振动进行了参数辨识和信号重建. 然而,他们所建立的振动信号模型为单一频率、 无衰减的简谐振动,并不适用于一般的机械振动.
机械振动信号和电磁通讯信号之间的本质区别在于机械振动信号的幅值会随时间而变化. 这会导致它们的模型不同,辨识方法也会不同. 需要指出的是,所谓的“随时间而变化”可能是衰减、 增强,甚至是保持恒定. 如果一个机械振动的振动状态在一段时间内保持稳定,就可以对其建立模型,并且经常用衰减系数来描述振动幅值随时间的变化趋势. 那么可以看出,根据振动幅值的不同趋势,衰减系数可以为正、 负或零. 所以,对于具有稳定振动状态的机械振动,可以期望提出一种通用的欠采样辨识方法,这也正是本文的目标.
最早由Roy等[8]提出的ESPRIT算法是一种高效的信号处理方法. 在通信工程领域它常用来估计信号的波达方向或者复合频率信号的频率. 很多学者[9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]都对ESPRIT算法的应用、 改进进行了研究. 并且,ESPRIT算法具有处理欠采样信号的潜能[4, 5]. 所以,本文将会借鉴ESPRIT算法的思想,来推导机械结构振动的欠采样辨识方法.
2 建模及欠采样 2.1 机械振动信号建模对于一般的机械振动信号,可以将其视为多个窄带振动信号的复合信号. 高频振动对系统动态特性影响很小,而且难于准确辨识和主动控制,因为其幅值很小,衰减很快. 所以当建模时,本文只对前M阶频率的振动信号建模,将高频阶次忽略. 被忽略的阶次将会投影到已建模的阶次上. 所以,如果某些具有较高能量的阶次被忽略,就会产生较大的辨识误差; 但如果所有主要的阶次都被包含在模型中,被忽略的阶次所产生的影响就是微小的. 参数M可以根据经验选取,其应该足够大,保证所有可能被激发的主要阶次都包含在模型中. 但过大的M将会增加不必要的计算负担. 对于一般的机械结构振动,多数时候将M取为3就足够了,那么待辨识的机械振动时域信号可用如下模型表示:
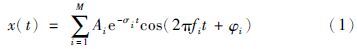
需要特别说明的是辨识过程中的噪声问题. 对于本文所讨论的问题,噪声主要来源于被忽略的高频振动信号分量. 对于机械结构振动,高频阶次通常无法保有较高的能量,所以不会发生大噪声的情况,无法回避的噪声只会对辨识结果造成微小的影响.
2.2 对振动信号欠采样如果以采样频率Fs对x(t)进行欠采样,得到的离散信号可表示为

如果定义A-i=Ai,σ-i=σi,f-i=-fi,φ-i=-φi,i=1,…,M,则:
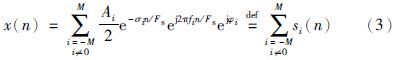
设总共采集了N个欠采样点,N≥4M. 令:


 ,i=-M,…,-1,1,…,M.
,i=-M,…,-1,1,…,M.

欠采样频率Fs的选取应该满足: A为满秩矩阵. 此时表明所建模的M阶振动信号在欠采样频率Fs下是可区分的,即在所建模的M阶振动中,只要某一阶振动处于被激发状态,在欠采样频率Fs下,就可以将这一阶振动信号从整体振动信号中分离出来.
事实上,对Fs的限定条件可以具体化为


限定条件(8)可以等价地表示为


根据奈奎斯特采样定理,对振动信号进行欠采样就会产生频率混叠现象. 这意味着欠采样之后,信号的频率信息已经丢失了. 要在欠采样的前提下对振动信号进行观测,就需要在欠采样点之外,另外附加一些信息. 本文提出ASP (adding sampling points)方法,ASP可以分为辨识振动频率、 辨识衰减系数、 匹配和频率修正及重建振动信号4个步骤. 频率解混叠与衰减系数的准确辨识之间经常是存在矛盾的[20]. 本文中,对振动频率和衰减系数分别辨识,然后再将它们匹配成对,以此解决这种矛盾.
3.1 辨识振动频率ASP即附加采样点法. 附加采样点,是指当对x(t)进行欠采样时,在每个采样点之后都需要额外增加的一个采样点. 即若t=t0为采样点,则t=t0+τ也将被采样. 其中τ应该满足τ<1/2fM.
在ASP中,数据采集单元实际上是以符合奈奎斯特采样定理的频率对振动信号进行采样的. 然后,从原始采样数据中抽取欠采样数据,以达到减少数据传输量的目的. 那么,附加采样点的产生就是自然而然的. 只需在抽取欠采样数据时,将附加采样点一同抽取出即可.
附加采样点序列可表示为

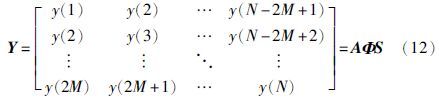

在传统的ESPRIT算法中,辨识过程中使用的是相关矩阵. 虽然相关矩阵具有充分利用采样数据的优势,但是它容易陷入病态状态,并且计算量较大[20]. 在本文中,用平均值矩阵取代了相关矩阵,克服了病态问题,减小了计算量,同时仍然充分地利用了采样数据.
令Xi=X[∶,i∶ i+2M-1],Yi=Y[∶,i∶i+2M-1],即Xi为X的第i列至第i+2M-1列构成的方阵,Yi意义与此类同. 可得

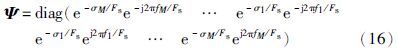

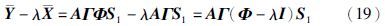
矩阵X,Y的秩与振动的激发状态直接相关. 可以看到,对于λ=e-σiτe±j2πfiτ(i=1,…,M),当第i阶振动被激发时,它可以减小矩阵Y-λX的秩; 反之当第i阶振动未被激发时,它对矩阵Y-λX的秩是没有影响的. 受此启发,本文将广义特征值重新定义如下:
定义1 对于矩阵束{Y,X},其中Y、 X都是实对称矩阵,它的广义特征值λ定义为所有使得矩阵Y-λX的秩减小的取值.
fi(i=1,…,M)中所有被激发的振动频率都可以通过求解矩阵束{Y,X}的广义特征值的辐角来进行辨识. 矩阵束的广义特征值的求法参见附录.
理论上,通过求矩阵束{Y,X}的广义特征值的模值也可以实现对于σi(i=1,…,M)的观测. 但实际上,这样算出的衰减系数的误差往往非常大. 这是由于在典型的机械振动中,衰减系数相对于振动频率来说是一个小量. 当要求τ<1/2fM时,会造成σiτ(i=1,…,M)是很小的量. 在这种情况下,利用e-σiτ来观测σi(i=1,…,M)是不抗扰动的. e-σiτ的微小变化就能引起σi的较大误差.
3.2 辨识衰减系数设:


从式(22)中可知,矩阵束{X″,X′}的广义特征值为λ=e-σim/Fse±j2πfim/Fs,其中i=1,…,M,并且第i阶振动是被激发的. 所以,可以通过求矩阵束{X″,X′}的广义特征值的模值,实现对振动信号衰减系数的观测. 一般情况下有m/Fs$ \gg $τ,所以这种观测衰减系数的方法可以得到较为准确的结果.
3.3 匹配以及频率校正本文利用差异度法匹配振动频率和衰减系数. 差异度法的计算量很小,并且在匹配过程中已辨识出的振动频率还可以得到校正.
因为发生了频率混叠,所以通过矩阵束{X″,X′}的广义特征值无法直接辨识振动频率. 但有:

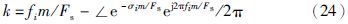
定义2 对于一个振动频率fj和一个衰减系数σi,差异度Δ(fj,σi)定义为

理论上,Δ(fi,σi)=0. 而实际上,由于采样误差、 建模误差的存在,Δ(fi,σi)一般不会等于0. 此时,Δ(fi,σi)就成为了修正振动频率fi的依据. 当Δ(fi,σi)≠0时,应该修正在3.1节中得到的fi的值,使得Δ(fi,σi)=0.
由于在3.1节和3.2节中分别辨识了振动频率和衰减系数,此处可以得到差异度矩阵:

(1) 在Δ中找到具有最小绝对值的元素或元素之一;
(2) 对应于此元素的振动频率和衰减系数相匹配;
(3) 从Δ中划去这个元素所在的行和列;
(4) 重复以上过程直到Δ变为空矩阵.
下面考查保证匹配正确性的条件. 要保证第i阶振动匹配的正确性,需要满足如下3个条件:


在配对过程中,会得到Δ(fi,σi). 对振动频率校正的方法为,将fi更新为fi-Δ(fi,σi)Fs/m. 其中i=1,…,M,并且第i阶振动是被激发的.
3.4 重建振动信号在完成机械振动的各阶振动频率和衰减系数的辨识之后,有时还需要进一步对各阶振动的幅值和相位进行解算,以完成振动信号的重建. 对机械振动信号欠采样得到的离散信号可表示为




在得到机械振动的所有参数之后,就可以实现对于振动信号的重建了.
4 仿真设待辨识机械振动信号为

以4 Hz的频率对其进行欠采样,采样长度为100,得到欠采样序列. 并且在延迟0.01 s之后进行附加欠采样,得到附加欠采样序列,即Fs=4,N=100,τ=0.01. 图 2所示为待辨识机械振动信号和欠采样序列.
|
| 图 2 待辨识机械振动信号及其欠采样序列 Fig. 2 The displacement signal of the mechanical vibration to be identified and its sub-Nyquist sampling sequence |
对该机械振动信号建模,取M=5. 分别辨识振动信号的频率和衰减系数,并对其配对. 前5阶振动频率和相应衰减系数的理论值,观测结果以及误差列于表 1. 从表中可以看到,观测结果是非常准确的.
| 第1阶 | 第2阶 | 第3阶 | 第4阶 | 第5阶 | |
| 频率理论值 /Hz | 7.1 | 14.2 | 21.3 | 28.4 | 35.5 |
| 频率辨识值 /Hz | 7.100 0 | 14.200 | 21.300 | 28.399 | 35.520 |
| 频率误差 /% | 0 | 0 | 0.000 5 | 0.002 8 | 0.055 2 |
| 衰减系数理论值 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 衰减系数辨识值 | 0.100 0 | 0.200 0 | 0.300 2 | 0.406 7 | 0.584 8 |
| 衰减系数误差 /% | 0 | 0 | 0.066 7 | 1.675 0 | 16.960 |
利用最小二乘法对相应的振幅和相位进行估计. 各阶频率对应的振幅值如图 3所示. 从图 3中可以看出,各阶振幅的估计结果也是非常准确的.

|
| 图 3 各阶频率对应的振幅值 Fig. 3 The vibration amplitudes corresponding to the frequencies of each order |
然后可以重建出完整的机械振动信号,如图 4所示为重建误差. 从图中可以看出,重建误差比原始振动信号小4个数量级. 这证明了本文所提出的方法的有效性.

|
| 图 4 重建误差 Fig. 4 The reconstruction errors |
在如图 5所示的实验平台上开展实验研究. 一根柔性金属杆被用来作为产生振动的金属结构,通过敲击法使其产生振动,对其产生的振动进行辨识. 在柔性金属杆的中点处安装一个加速度传感器,可以同时测量金属杆的第1阶和第2阶振动. 信号通过一台Lance放大器进行放大. 用NI CompactRIO作为数据采集和处理单元. 柔性金属杆的振动通过敲击来产生. 在数据采集和数据处理之间加入3 s的时延,来模拟遥操作系统的单边信息迟滞.

|
| 图 5 实验平台 Fig. 5 The experimental platform |
以2 048 Hz的采样频率采集振动信号,这是符合奈奎斯特采样定理的采样. 然后,从原始采样数据中抽取出欠采样数据,用以辨识振动信号参数以及重建振动信号. 将从欠采样数据中得到的结果与原始采样数据中包含的信息进行比较,以此对实验结果进行评价.
值得注意的是,在实验中分别辨识出的振动频率和衰减系数的个数可能是不相等的. 这主要是因为真实的振动信号的误差相对较大,可能导致在求解广义特征值时出现一些非法解. 非法解主要指的是不共轭的实数广义特征值,非法解应该舍去.
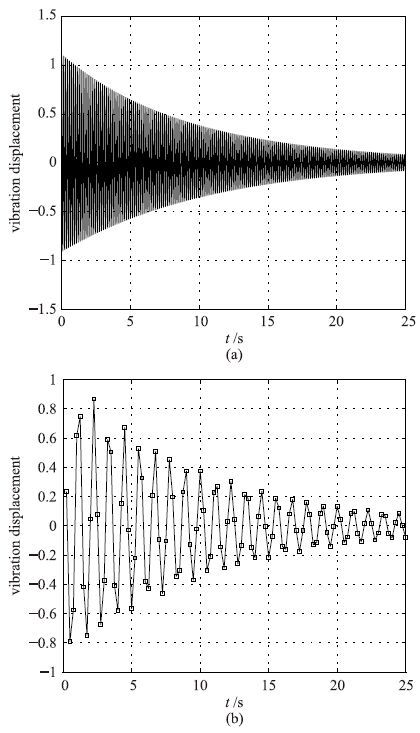
实验中得到的原始采样数据如图 6(a)所示. 以2 048/170 Hz的采样频率对实验中的机械振动进行欠采样,并且在延迟10/2 048 s后进行附加欠采样,即Fs=2 048/170,τ=10/2 048. 振动信号的欠采样序列如图 6(b)所示.

|
| 图 6 实验中得到的原始采样数据以及振动信号的欠采样序列 Fig. 6 The original sample obtained in the experiment and the sub-Nyquist sampling sequence of the vibration signal |
取M=3,对机械振动信号建模. 利用ASP法对欠采样数据进行辨识,最终得到了二阶振动. 实验中辨识出的振动频率分别为4.786 2 Hz、 26.510 8 Hz. 也可以对原始采样数据做FFT(fast Fourier transform),可以得到信号的前两阶振动频率分别约为4.75 Hz、 26.26 Hz. 可以看到,分别由ASP和FFT得到的频率辨识结果彼此是非常接近的. 如果将由ASP得到的对应于各阶频率的振动幅值与原始采样数据的FFT进行比较,也可以立即发现两幅图是非常相似的如图 7所示.

|
| 图 7 利用本文方法辨识出的对应于各阶频率的振动幅值及原始采样数据的FFT Fig. 7 The vibration amplitudes identified with the proposed method corresponding to the frequencies of each order,and the FFT of the original sample |
最后,通过辨识出的参数,机械振动信号可以被重建出来. 在图 8中同时画出了重建出的信号和重建误差,从中可以看出ASP法的有效性. 由于实验仪器精度的限制,实验中的重建误差自然地要比仿真中的大一些.

|
| 图 8 重建信号以及重建误差 Fig. 8 The reconstructed signal and the reconstruction error |
本文参考ESPRIT算法,提出了一种应用于遥操作系统的机械结构振动辨识方法. 用平均值矩阵取代了传统ESPRIT算法中的相关矩阵,在保证充分利用采样数据的同时,克服了相关矩阵易产生病态的问题,并减小了计算量; 对振动频率和衰减系数分别进行辨识,然后再将它们匹配成对,解决了频率解混叠和衰减系数准确辨识之间的矛盾; 利用差异度法匹配振动频率和衰减系数,计算量很小,并且在匹配过程中可以对辨识出的振动频率进行修正.
利用本文提出的方法进行了仿真研究和实验研究. 仿真结果显示了所提出的方法的正确性和高精度. 实验结果表明所提出的方法是可应用于实际的,并且尽管只利用了欠采样数据,却可以得到与FFT相似的结果. 总之,文中提出的方法不仅是可行的,而且是有效的. 附录 本文中求解矩阵束广义特征值的方法
本文中将矩阵束{Y,X}的广义特征值重新定义为: 对于矩阵束{Y,X},其中Y、 X都是实对称矩阵,它的广义特征值λ定义为所有使得矩阵Y-λX的秩减小的取值. 另外,根据本文的具体应用,X、 Y可以分解为如下形式:

对于实对称矩阵X,存在可逆矩阵P,使得


由式(1)和式(3)可得

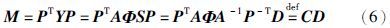




于是可以得到结论: 矩阵束{Y,X}的广义特征值就是矩阵Dr-1Mr的特征值,并且Dr和Mr都是容易获得的.
| [1] | Shi G M, Liu Z, Chen X Y, et al. A parallel sampling scheme for ultra-wideband signal based on the random projection[C]//IEEE International Symposium on Circuits and Systems. Piscataway, NJ, USA: IEEE, 2008: 2246-2249. |
| [2] | Maroosi A, Bizaki H K. Digital frequency determination of real waveforms based on multiple sensors with low sampling rates[J]. IEEE Sensors Journal, 2012, 12(5): 1483-1495. |
| [3] | 王玉兰, 刘娅, 李孝辉. 基于欠采样的频率测量方法[J]. 电子测量与仪器学报, 2010, 24(1): 45-49. Wang Y L, Liu Y, Li X H. A method of frequency measurement based on sub-nyquist sampling[J]. Journal of Electronic Measurement and Instrument, 2010, 24(1): 45-49. |
| [4] | 黄佑勇, 王激扬, 陈天麒. 基于欠采样的宽频段信号频率估计技术[J]. 电波科学学报, 2001, 16(2): 275-279. Huang Y Y, Wang J Y, Chen T Q. Wide-band frequency estimation with sub-Nyquist sampling[J]. Chinese Journal of Radio Science, 2001, 16(2): 275-279. |
| [5] | 王洪洋, 廖桂生, 吴云韬. 欠采样频率估计方法[J]. 电子学报, 2004, 32(12): 1978-1981. Wang H Y, Liao G S, Wu Y T, Frequency estimation with sub-Nyquist sampling[J]. Acta Electronica Sinica, 2004, 32(12): 1978-1981. |
| [6] | 李孟麟, 段发阶, 欧阳涛, 等. 基于叶尖定时的旋转机械叶片振动信号重建[J]. 机械工程学报, 2011, 47(13): 98-103. Li M L, Duan F J, Ouyang T, et al. Reconstruction of the blade vibration signal from rotating machinery based on blade tip-timing measurement[J]. Journal of Mechanical Engineering, 2011, 47(13): 98-103. |
| [7] | 欧阳涛, 段发阶, 李孟麟, 等. 恒速下旋转叶片同步振动辨识方法[J]. 天津大学学报, 2011, 44(8): 742-746. Ouyang T, Duan F J, Li M L, et al. Method for identifying rotating blade synchronous vibration at constant speed[J]. Journal of Tianjin University, 2011, 44(8): 742-746. |
| [8] | Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1989, 37(7): 984-995. |
| [9] | Liu F L, Wang J K, Yu G. An OTST-ESPRIT algorithm for joint DOA-delay estimation[C]//IEEE International Symposium on Communications and Information Technology. Piscataway, NJ, USA: IEEE, 2004: 734-738. |
| [10] | Liu C F, Liao G H. Real-value space ESPRIT algorithm and its implement[C]//International Conference on Wireless Communications, Networking and Mobile Computing. Piscataway, NJ, USA: IEEE, 2006: 1-5. |
| [11] | Inagaki Y, Kikuma N, Hirayama H, et al. DOA estimation of desired signals by cyclic ESPRIT based on noise subspace and its performance improvement[J]. Electronics and Communications in Japan Part I-Communications, 2007, 90(11): 95-104. |
| [12] | Gabai R, Bucher I. Excitation and sensing of multiple vibrating traveling waves in one-dimensional structures[J]. Journal of Sound and Vibration, 2009, 319(1/2): 406-425. |
| [13] | Tripathy P, Srivastava S C, Singh S N. A modified TLS-ESPRIT-based method for low-frequency mode identification in power systems utilizing synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2011, 26(2): 719-727. |
| [14] | El Kassis C, Picheral J, Fleury G, et al. Direction of arrival estimation using EM-ESPRIT with nonuniform arrays[J]. Circuits Systems and Signal Processing, 2012, 31(5): 1787-1807. |
| [15] | Ge S B, Sun C Y. The DOA of wideband signals estimation by using ESPRIT based on K-means[C]//International Symposium on Instrumentation and Measurement, Sensor Network and Automation. Piscataway, NJ, USA: IEEE, 2013: 856-859. |
| [16] | Steinwandt J, Roemer F, Haardt M. Performance analysis of ESPRIT-type algorithms for non-circular sources[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ, USA: IEEE, 2013: 3986-3990. |
| [17] | Chen C, Zhang X F. A RD-ESPRIT algorithm for coherent DOA estimation in monostatic MIMO radar using a single pulse[J]. International Journal of Electronics, 2014, 101(8): 1074-1085. |
| [18] | 李毅, 杨菊平. 一种基于ESPRIT的改进算法[J]. 信号处理, 2009, 25(3): 508-511. Li Y, Yang J P. An ESPRIT-based improved algorithm[J]. Signal Processing, 2009, 25(3): 508-511. |
| [19] | 周庆辉, 许宗泽, 靳学明. 一种改进的ESPRIT测向算法[J]. 雷达科学与技术, 2005, 3(3): 148-151. Zhou Q H, Xu Z Z, Jin X M. A modified ESPRIT algorithm for direction finding[J]. Radar Science and Technology, 2005, 3(3): 148-151. |
| [20] | Chen P, Liu S J, Cui L, et al. A mechanical vibration identification method for sub-Nyquist sampling based on esprit-like algorithm[C]//11th IEEE International Conference on Control & Automation. Piscataway, NJ, USA: IEEE, 2014: 1292-1297. |
| [21] | 计文军, 杨海彬, 王艳华, 等. 基于Matlab的实对称矩阵对角化[J]. 内江科技, 2007, 28(4): 36. Ji W J, Yang H B, Wang Y H, et al. Diagonalization of real symmetric matrices based on Matlab[J]. Nei Jiang Ke Ji, 2007, 28(4): 36. |



