2. 东北大学信息科学与工程学院,辽宁 沈阳 110819
2. College of Information Science and Engineering, Northeastern University, Shenyang 110819, China
手背静脉识别是在特定波长的近红外光源的照射下,通过获取的手背静脉图像来进行身份识别的. 与其它生物识别技术相比,静脉识别具有以下优势: 活体识别、 特定光源、 内部特征、 非接触式图像采集. 相对于其它生物特征识别技术,静脉识别具有更好的接受程度与更高的安全等级[1].
近年来,研究人员主要针对静脉图像的特征提取进行了研究: 2004年,Lin首先将多尺度理论引入到静脉识别算法[2]. 随后,Liu等人将多级小波理论应用在了静脉特征过程中[3]. 文[4, 5, 6, 7]利用了Gabor滤波器提取了静脉图像的特征,解决了小波描述高频信息方向性缺陷的难题. 除采用灰度特征以外,研究人员同样对二值静脉特征也展开了分析与研究. 2005年,Ding等采用了一种自适应阈值对图像进行二值化处理,进而采用脉络交叉点与端点作为特征[8]. 同样利用特征点,Kumar等将特征点间围成的三角形形状作为静脉图像的特征[9]. Lee等对其进行了进一步的改进,将滤波结果进行了位串编码[10]与二值编码[11, 12],增加静脉特征的有效性. 而后,Wu等对编码方法进一步改进,提出了采用最小化方向性编码的思想提取静脉特征[13]. 获取静脉特征后,学者针对特征的降维问题展开了分析: Wang等提出了“Laplacianpalm”方法,有效的获取了静脉特征基[14]; 而Khan等则利用改进主成分分析法实现了静脉特征的降维[15]; 随后,Liu等陆续采用了独立主成分分析[16]与局部保持投影[17]的策略实现了特征的降维与分类.
以上研究取得了一定的成果,但关于特征有效性与特征意义的讨论仍较为罕见. 以上方法获取的特征向量中元素可以是正数,也可以是负数. 从数学的观点来说负数是有意义的; 但从实际应用出发,负数特征向量元素很难被解释,如基向量系数、 概率统计值等信息. 为解决这一问题,这里将提出一种基于非负矩阵分解(nonnegative matrix factorization,NMF)思想的静脉识别算法.
2 静脉图像初始特征提取采集静脉图像后,需对静脉图像进行预处理,如图 1与图 2所示.

|
| 图 1 静脉图像预处理框图 Fig. 1 Block diagram of vein image preprocessing |
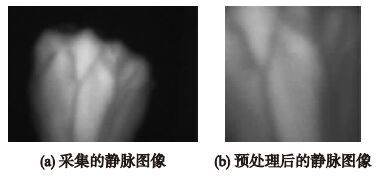
|
| 图 2 静脉图像预处理结果 Fig. 2 Vein image preprocessing result |
为获得较为完整图像全局与局部特征,这里首先将预处理后的静脉图像F进行分块处理. 假设归一化后的静脉图像大小为T×T像素,子图像大小为L×L像素,为了避免边界效应,相邻子图像间的重叠像素数目为K,则分块后子图像数目如式(1),分块方法如图 3所示.
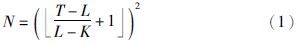

|
| 图 3 图像分块示意图 Fig. 3 Sketch map of dividing image into blocks |
由于算法将采用非负矩阵分解思想进行特征提取,因此提取的初始静脉特征应具有非负性的性质. 这里将每一子图像中像素的均值与平均梯度幅值作为该子图像的初始特征,其中,均值Mi,j可以描述子图像的低频信息,而平均梯度幅值Ai,j可描述子图像的较高频信息,获取以上两个特征值如式(2)和式(3)所示:
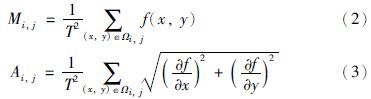
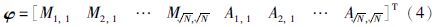
假设训练样本中包含m个静脉对象,每个静脉对象包含n个样本,经过初始特征提取后,形成初始特征矩阵φ:
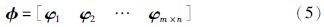
由NMF定义可知,对于给定的非负矩阵φ∈Ru×v,需将其近似分解为两个非负矩阵W∈Ru×r与H∈Rr×v的乘积[18]:

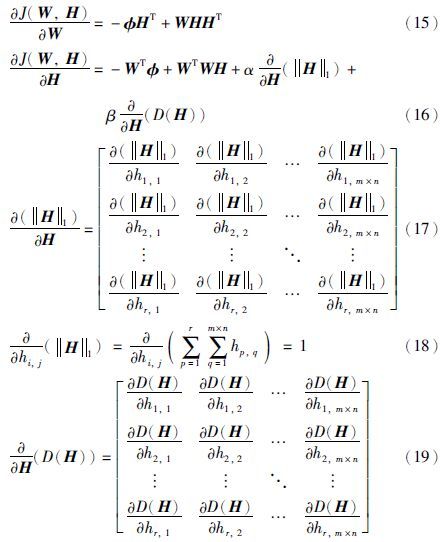
除非负性约束以外,在初始特征矩阵φ分解过程中还应满足以下2种约束条件:
(1) 系数向量稀疏性. 初始特征矩阵φ经非负分解后,将形成新的特征基,而每一静脉图像特征将被少数特征基所影响,即分解后的系数向量h将具有较强的稀疏性,因此需要将稀疏性作为NMF模型的约束条件之一,即‖H‖0值应尽可能小.
(2) 系数向量可区分性. φ经非负分解后,得到的系数向量h将作为静脉图像新的特征,对于有监督的特征训练,不同静脉对象的特征间将具有较大的区分性,因此需要将特征可区分性作为NMF的另一约束条件,即描述不同静脉对象特征向量的余弦距离函数D(H)值也将尽可能小.
根据以上分析,可获得增加以上两种约束条件后的NMF模型:
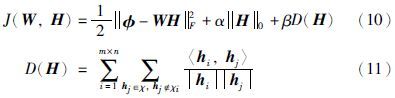
根据压缩感知及稀疏表达理论,如果系数向量足够稀疏,求解0范数问题可以转化为求解1范数问题[19],求‖H‖0的最小值将等价于求‖H‖1的最小值,从而获得改进后的NMF模型:
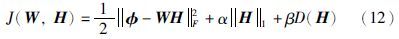
对于提出的改进NMF模型,将采用梯度投影法对其进行求解,该方法核心思想是当迭代点在可行域内部时,取该点处的负梯度方向为可行下降方向; 当迭代点在可行域边界上时,取该点处负梯度方向在可行域边界上的投影产生的一个可行下降方向.
改进的NMF模型(12)可以转化为式(13):
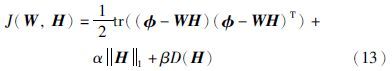
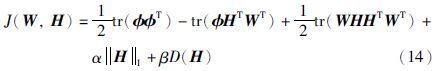
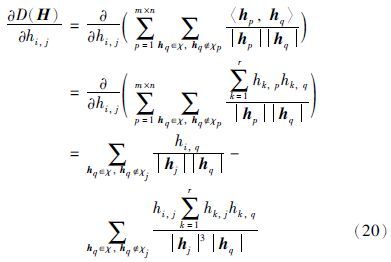
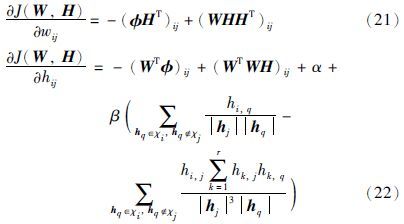
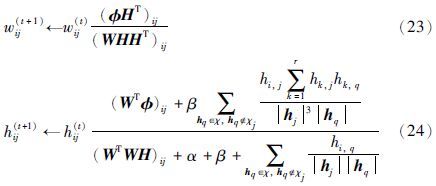
根据文[20, 21],具有稀疏约束的非负矩阵分解模型是收敛的,即存在最小值; 本文提出的分解模型增加了另外一项约束D(H)=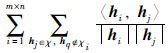 ,其中0<
,其中0<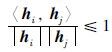 ,因此D(H)一定存在最小值,即改进后的模型也一定拥有最小值.
,因此D(H)一定存在最小值,即改进后的模型也一定拥有最小值.
以上为静脉识别过程中特征基的训练过程,而完整的识别系统流程如下:
| Input: 训练样本集合,假定m个静脉对象,每个静脉对象包含n个样本,平衡因子α与β; |
| Step 1 初始化分解矩阵W(0)与H(0),矩阵元素为[0,1]区间随机值; |
| Step 2 设置迭代最大次数η,误差阈值e,迭代次数计数值t=0,J(W(0),H(0)); |
| Step 3 t←t+1; |
Step 4 求解建立的非负矩阵分解模型;
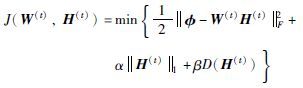
|
|
Step 5 if |J(W(t),H(t))-J(W(t-1),H(t-1))<ε or t>η. goto Step 6. else 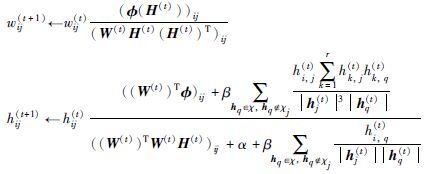
end if |
| Step 6 获取最终的分解矩阵W(f)(基矩阵)与H(f)(训练样本特征矩阵); |
Step 7 给定待匹配的静脉图像,对其初始特征fx基于特征基分解,获得新的特征向量:
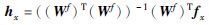
|
Step 8 计算特征向量与训练样本特征向量的余弦距离,并与阈值比较,获得识别结果:
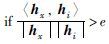
else hx∉χi end if |
本系统的图像采集装置采用环形阵列近红外光源,CCD图像传感器,如图 4所示.

|
| 图 4 静脉图像采集设备 Fig. 4 Vein image acquisition equipment |
对273个人的手背静脉进行了图像采集,其中每个静脉对象在多种自然光强、 多种手背伸入角度条件下采集的,共采集10次,其中8幅图像作为训练样本,另外两幅作为测试样本,并进行交叉检验,即所有样本均有机会作为训练样本与测试样本,部分静脉图像样本如图 5所示.
|
| 图 5 部分静脉样本 Fig. 5 Part vein samples |
感兴趣区域提取后的静脉图像为256×256像素,分块后子图像为7×7像素,相邻子图像重叠3个像素. 在提出的NMF模型中,参数α与β分别选取{1,0.1,0.01},最大迭代次数为η=1 000,根据经验误差阈值ε设为0.5,分解后基向量数目r分别选取{100,150,200,250}.
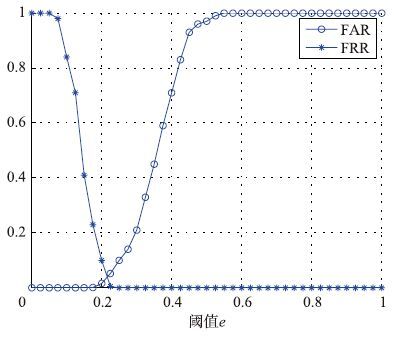
本系统将采用错误接受率(false acceptance rate,FAR)与错误拒绝率(false rejection rate,FRR)作为评价识别算法性能的测度. 例如,当α=0.1,β=0.1,r=200时,该系统识别性能如图 6所示.
|
| 图 6 识别算法性能曲线 Fig. 6 Performance curves of the recognition algorithm |
由图 6可以看出,当α=0.1,β=0.1,r=200,阈值e=0.232时,识别算法具有最好的性能,这里将FAR+FRR作为衡量识别算法性能的测度.
当选取不同的模型参数α、 β、 r时,识别系统性能如表 1所示.
| FAR+FRR | r=100 | r=150 | r=200 | r=250 | |
| α=0.01 | 0.075 7 | 0.068 5 | 0.083 2 | 0.063 4 | |
| β=0.01 | α=0.1 | 0.063 3 | 0.063 0 | 0.062 2 | 0.061 2 |
| α=1 | 0.067 2 | 0.074 5 | 0.070 4 | 0.063 5 | |
| α=0.01 | 0.045 8 | 0.050 5 | 0.061 1 | 0.046 4 | |
| β=0.1 | α=0.1 | 0.047 0 | 0.044 7 | 0.042 4 | 0.048 2 |
| α=1 | 0.051 2 | 0.060 1 | 0.064 6 | 0.061 7 | |
| α=0.01 | 0.056 3 | 0.060 2 | 0.061 2 | 0.063 5 | |
| β=1 | α=0.1 | 0.061 6 | 0.061 9 | 0.058 6 | 0.067 8 |
| α=1 | 0.074 9 | 0.064 9 | 0.065 3 | 0.068 1 | |
可以看出,当α=0.1,β=0.1,r=200时,识别算法具有最好的性能.
5.2 不同识别算法的实验结果比较及分析由于提出的静脉识别算法为基于子空间分解的降维与识别算法,因此这里选取了3种已有的基于子空间分解思想的算法进行了比较. 对于建立的静脉样本数据库,选取同样的初始特征,分别选取了文[14]的拉普拉斯特征基、 文[15]的主成分分析特征基、 文[17]的局部保持投影特征基、 原始NMF特征基分解方法本文识别算法比较,比较结果如表 2所示.
可以看出,将FAR与FRR作为评价识别算法性能的测度时,提出算法的性能要优于其它算法,较好地解决了其它分解算法中因数据过拟合、 优化模型时陷于局部最优等缺陷.
本实验环境采用Matlab 2010b,PC机处理器为i5-4460 CPU 3.2 GHz,8 G内存. 由表 2可以看出,提出算法的识别时间略高于文[15]与原始NMF算法; 而2.18 s的运行速度基本可以满足识别系统的实时性要求.
6 结论图像经过特征基分解后,负数分解系数往往缺少实际意义,而为使手背静脉图像特征描述更具实际意义,本文提出了一种改进的非负矩阵分解特征提取算法. 该方法除考虑分解系数特征向量的非负性以外,同时对特征向量的稀疏性与可区分性加以约束,使提取的静脉特征在识别过程中更具有效性. 实验表明,对于建立的静脉样本数据库,提出的算法具有较高的性能,FAR与FRR测度值可分别降低至0.020 2和0.022 2. 同样,算法在一些方面仍需要进行改进,如识别系统的实时性需进一步提高,样本库中样本数量在以后的研究过程中也需进一步增加.
| [1] | 贾旭, 曹玉东, 孙福明, 等. 基于无参考质量评价模型的静脉图像采集方法. 电子学报, 2015, 43(2): 236-241. Jia X, Cao Y D, Sun F M, et al. Vein image acquisition method based on quality assessment model without reference[J]. Acta Electronica Sinica, 2015, 43(2): 236-241. |
| [2] | Lin C L, Fan K C. Biometric verificatio using thermal images of palm-dorsa vein patterns[J]. Transactions on Circuits and Systems for Video Technology, 2004, 14(2): 199-213. |
| [3] | 刘铁根, 王云新, 李秀艳, 等. 基于手背静脉的生物特征识别系统[J]. 光学学报, 2009, 29(12): 3339-3343. Liu T G, Wang Y X, Li X Y, et al. Biometric recognition system based on hand vein pattern[J]. Acta Optica Sinica, 2009, 29(12): 3339-3343. |
| [4] | Han W Y, Lee J C. Palm vein recognition using adaptive Gabor filter[J]. Expert Systems with Applications, 2012, 39(18): 13225-13234. |
| [5] | Wang J X, He Y Q, Zhu J D, et al. Palm vein for efficient person recognition based on 2D Gabor filter[M]//SPIE Proceedings: Vol. 8712. Bellingham, WA, USA: SPIE, 2013: 87120K. |
| [6] | Hsu C B, Lee J C, Hao S S, et al. Dorsal hand vein recognition using Gabor feature-based 2-directional 2-dimensional principal component analysis[J]. Advanced Science Letters, 2012, 8(1): 813-817. |
| [7] | Wang R, Wang G Y, Chen Z, et al. A palm vein identification system based on Gabor wavelet features[J]. Neural Computing and Applications, 2014, 24(1): 161-168. |
| [8] | Ding Y H, Zhuang D Y, Wang K J. Hand vein recognition based on multi supplemental features of multi-classifier fusion decision[C]//Proceedings of the IEEE International Conference on Mechatronics & Automation Niagara Falls. Piscataway, NJ, USA: IEEE, 2006: 1970-1975. |
| [9] | Kumar A, Prathyusha K V. Personal authentication using hand vein triangulation and knuckle shape[J]. Transactions on Image Processing, 2009, 9(18): 2127-2136. |
| [10] | Lee J C, Lee C H, Hsu C B, et al. Dorsal hand vein recognition based on 2D Gabor filters[J]. The Imaging Science Journal, 2014, 62(3): 127-138. |
| [11] | Hsu C B, Lee J C, Chuang S J, et al. Gaussian directional pattern for dorsal hand vein recognition[J]. The Imaging Science Journal, 2014, 63(1): 54-62. |
| [12] | Lee J C, Lo T M, Chang C P. Dorsal hand vein recognition based on directional filter bank[M]//Signal, Image and Video Processing. Berlin, Germany: Springer-Verlag, 2014: 1-8. |
| [13] | Wu K S, Lee J C, Lo T M, et al. A secure palm vein recognition system[J]. Journal of Systems and Software, 2013, 86(11): 2870-2876. |
| [14] | Wang J G, Yau W Y, Suwandy A, et al. Person recognition by fusing palmprint and palm vein images based on “Laplacianpalm” representation[J]. Pattern Recognition, 2008, 41(5): 1514-1527. |
| [15] | Khan M H, Subramanian R K, Khan N A M. Low dimensional representation of dorsal hand vein features using principle component analysis[J]. Engineering and Technology, 2009, 37, 1091-1097. |
| [16] | Liu J, Cui J J, Xue D Y, et al. Palm-dorsa vein recognition based on independent principle component analysis[C]//2011 International Conference on Image Analysis and Signal Processing (IASP). Piscataway, NJ, USA: IEEE, 2011: 660-664. |
| [17] | Liu J, Xue D Y, Cui J J, et al. Palm-dorsa vein recognition based on locality preserving projection[J]. Journal of Information and Computational Science, 2011, 8(16): 3911-3919. |
| [18] | Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-791. |
| [19] | 杨旗, 薛定宇. 基于稀疏表示及分段帧差能量图的步态识别[J]. 信息与控制, 2013, 42(1): 27-32. Yang Q, Xue D Y. Gait recognition based on sparse representation and segmented frame difference energy image[J]. Information and Control, 2013, 42(1): 27-32. |
| [20] | Wang Y X, Zhang Y J. Nonnegative Matrix Factorization: A comprehensive review[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(6): 1336-1353. |
| [21] | Han H, Liu S J, Gan L. Non-negativity and dependence constrained sparse coding for image classification[J]. Journal of Visual Communication and Image Representation, 2015, 26: 247-254. |



