面对弹道导弹及高超声速目标等对国家安全日益严重的威胁，预警卫星作为远程预警系统的重要组成部分受到各国的高度重视[1, 2, 3]，如美国近期部署的天基红外卫星系统及在研的天基跟踪与监视系统. 这类系统使用可见光和短波红外获取传感器对目标进行全程探测、 跟踪和识别. 由于红外探测器探测范围有限，当系统面对较多预警任务时，需要考虑如何对天基预警系统资源进行合理调度，使系统能有效的对多个来袭目标进行探测和跟踪[4].
针对预警卫星资源调度问题，近年国内外学者都进行了较为广泛的研究[5, 6, 7, 8, 9]. Sarkheyli[5]、 Wang[6]等对地球观测卫星进行了研究，分别采用区间图着色问题和混合蚁群算法进行求解. 阎志伟[7]通过建立传感器调度模型及相应评价指标体系，设计了并行禁忌遗传算法，该算法采用并行禁忌思想改善遗传算法(genetic algorithm，GA)的搜索性能，提高了算法的收敛速度和精度. 郭浩波等[8]结合GA和模拟退火算法(simulated annealing，SA)的特点，提出GASA算法，提高了算法的寻优能力，但不适用于规模较大的系统. 上述研究主要集中于算法的设计，忽略了预警任务本身的特性. 冯明月等[9]从预警任务特点出发建立了较好的调度模型，然后采用改进的粒子群算法(particle swarm optimization，PSO)对该问题求解，但与传统PSO相比，改进效果不是很明显.
本文针对文[8]和文[9]存在的问题，借鉴文[9]对弹道导弹目标探测任务进行分解，给出了资源调度模型. 然后结合粒子群算法和遗传算法的优点，采用一种混合优化算法对该问题进行求解. 最后通过仿真实例验证了模型和算法的有效性.
2 分解与调度模型 2.1 预警任务分析由于导弹在大部分时间内处于其飞行中(对于总飞行时间为30 min的导弹，中段飞行时间约为25 min)，因此对导弹目标飞行中段的监视与跟踪十分重要，是弹道导弹防御的关键环节[1]. 本文研究的是当低轨道卫星在对飞行中段进行目标探测、 跟踪与识别等时需考虑的卫星资源调度和分配问题. 由于弹道导弹的弹道具有可计算性，因此可通过主动段探测得到目标弹道，并依据此假设进行目标任务的分解.
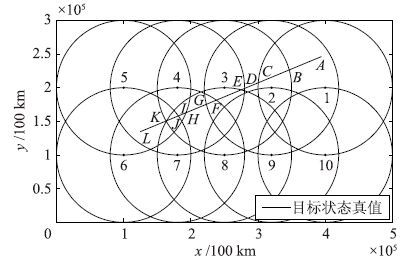
星载探测器执行探测任务时具有一个可探测时间窗口，在该时间窗口内可对目标进行探测和跟踪. 卫星分布与目标位置关系如图 1所示，线段AL是目标弹道，对于卫星1而言，AC段是其可探测窗口，在该时间段内目标才能够被探测到.
|
| 图 1 目标可探测时间窗 Fig. 1 Time window for detecting target |
由于预警卫星系统由多颗卫星构成，执行多目标探测任务时，存在多颗卫星接力跟踪的可能. 整个预警过程作为单个任务很难完成有效调度，因此需对预警任务进行分解，得到子任务序列，下面介绍具体任务分解方法.
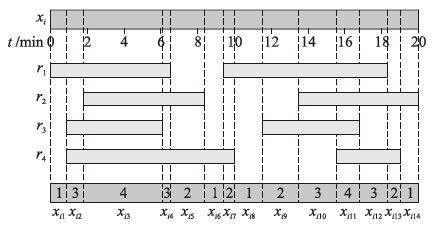
2.2 任务分解方法本文参考文[9]的任务划分方法，将预警任务分解为子任务序列. 如图 2所示，基于传感器r1～r4对该任务可探测时间窗的起止节点，将整个预警任务分解为14个子任务xij. xij含有两类重要信息：
(1) 该子任务的起始和终止时间点；
(2) 在子任务时间窗内，所有可对目标进行探测的卫星集合.
为满足在预警系统连续跟踪要求，任务分解时需考虑以下约束条件[9]：
|
| 图 2 预警任务分解与探测资源对应关系 Fig. 2 The relationship between warning task decomposition and detecting resource |
约束1 子任务可探测资源集合在其对应的时间区间内不发生变化.
约束2 子任务执行时间不能过短. 对于每次探测对象的转变，预警卫星的星载探测器都需要进行一系列操作来调整，同时需要足够时间来得到具有一定使用价值的探测数据，因此子任务的最短执行时间为Lmin.
约束3 子任务执行时间不宜过长. 若子任务执行时间过长会造成子任务数量过少、 调度性能降低. 子任务最长执行时间为Lmax，并规定Lmax≥2Lmin以保证调度灵敏度.
根据上述约束条件将预警任务分解为由多个执行时间较短的子任务组成的序列，具体步骤如下：
(1) 统计目标进出所有卫星探测范围的时间点，得到整个预警任务中每个卫星的可探测时间窗口.
(2) 为保证整个子任务可探测资源集不发生改变，本文对上述时间点进行排序，并删除相同时间点，得到连续的探测时间片. 同时，记录在每个时间片内能够探测到目标的所有资源编号，作为该时间片内的可探测资源集合.
(3) 将长度大于Lmax的时间片继续划分，根据以下方法进行：
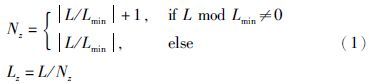
(4) 若相邻时间片长度均小于Lmin，时间片累加长度不大于Lmax且各时间片可探测资源集合的交集不为空，则合并这些时间片.
(5) 经过步骤(4)后，若仍有时间片长度小于Lmin，则与相邻时间片进行合并，但需保证合并后，时间片不大于Lmax，可探测资源集合的交集不为空.
(6) 在经过了步骤(4)和步骤(5)合并之后，丢弃不满足约束2的时间片，保留下来的时间片则为该任务的子任务序列.
将某预警任务Xi分解并得到子任务序列后，可把目标探测任务的资源调度问题转换为约束满足问题，即如何合理地选择卫星对子任务进行探测. 建立起数学模型后可采用优化算法对子任务序列中采用何种资源调度策略进行寻优，得到最优或满意的总体资源调度策略.
2.3 调度模型各预警任务经过任务分解后，得到一系列连续的子任务. 假设轨道上有NR个卫星｛1，2，…，NR｝，存在N个预警任务｛T1，T2，…，TN｝，任务Ti的优先级为Pi，包含了Ni个子任务｛Ti1，Ti2，…，TiNi｝. 子任务Tij是由时间片的端点sij、 fij及该时间片中所有可探测资源集合Rij组成的结构体. 该问题的数学描述如下：
适应度函数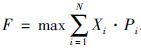
. 函数表示经过调度后完成的预警任务的加权和. 其中，Xi表示某个任务是否能够被完成，Pi为该任务对应的优先级.
约束条件有： 任务约束CT，子任务约束CCT和资源约束CS三类. CT： 调度任务Xi是否成功取决于被探测时间占任务总时间的比例，若超过阀值λ，认为该任务完成. CCT： 若子任务由资源Rk执行且Rk∈Rij，则子任务可完成. 同时，为提高资源利用率，一个子任务只需一个资源执行. CS： 由于探测器在两个任务间的转化无法瞬时完成，某一时刻同一探测器只能探测一个子任务； 执行一个子任务所需资源量为C且一个卫星资源总量Sk.
决策变量： Xi为第i个预警任务是否完成； xijk表示第i个任务的第j个子任务是否由资源Rk探测.
调度模型如下：
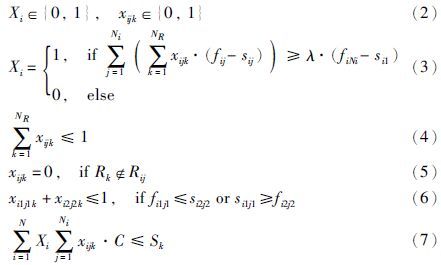
GA和PSO都起源于生物学，使用适应度函数来评价系统，而且能进行一定的随机搜索. GA的交叉、 变异过程使其具有广泛的空间搜索能力，不易陷入局部最优，适应于规模较大系统. 但在进化时没有考虑到个体自身的发展，算法收敛速度相对较慢[10, 11]. 而PSO考虑自身发展，收敛速度快，只是容易陷入局部最优[12, 13].
针对GA和PSO算法的不足之处，学者们进行了各种改进[14, 15, 16, 17]. 本文在上述研究的基础上，结合两类算法的优点，在求解资源调度问题时采用GA-PSO混合优化算法，重点解决了粒子的编解码问题及粒子的进化方式，现具体介绍如下.
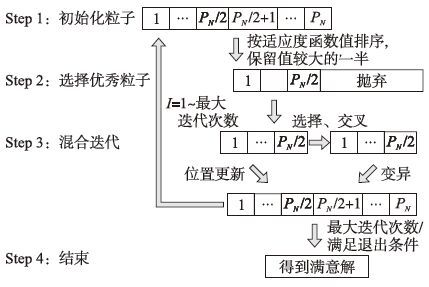
3.1 GA-PSO算法流程GA-PSO算法流程图如图 3所示，算法具体步骤如下：
|
| 图 3 GA-PSO算法流程图 Fig. 3 The block diagram of GA-PSO algorithm |
(1) 初始化. 生成符合本问题要求的初始种群，同时初始化初始粒子的更新速度vij.
(2) 选择优秀粒子. 首先计算p个粒子的适应度函数值并排序，将适应度函数值高的p/2个粒子作为优秀粒子保留.
(3) 迭代更新. 迭代过程采用混合迭代方法. 首先，采用传统PSO算法的粒子更新方式对保留的粒子进行更新，得到p/2个新粒子. 然后，对新粒子采用GA算法进行复制、 交叉、 变异等操作直到得到p/2个粒子. 最后，将两次得到的粒子组合成下一代p个粒子. 保证每次迭代之后种群总的数量不变.
(4) 结束： 判断是否达到最大迭代次数或者检验当前种群是否满足预设条件，若满足则停止迭代，得到最优或满意调度策略，否则继续进行步骤(3).
3.2 关键问题分析
(1) 粒子进化方式. 本文使用｛yij，i=1，2，…，N，j=1，2，…，Ni｝表示粒子个体. 一个粒子表示如式(8)所示，其中xij表示执行预警任务Ti的子任务Tij的资源序号，编码范围为｛0，1，2，…，NR｝，当yij=0时，表示子任务Tij不被执行，每个粒子的长度为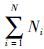
.
为了使粒子位置更新时可访问调度模型，在粒子与决策变量间建立联系，方法如式(9)所示：
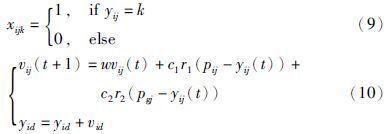
(2) 粒子编解码策略. 由上述可知，在粒子初始化和PSO更新策略时，采用的是整数编码方式，而GA算法采用的是二进制编码方式. 由于GA-PSO算法采用混合迭代方式，因此需要两套编解码方式[19, 20]. 这两种方式之间涉及到编码转换问题，即对PSO整数粒子进行二进制化，转化为GA算法的二进制编码方式.
当粒子经过PSO算法更新后进行GA算法操作时，粒子被称作“染色体”，每条“染色体”由多个“基因”组成，需要采用GA二进制编码方式对染色体进行编码. “基因”由长度为Lg的二进制数组成.
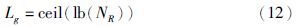
考虑到基因编码可能超过最大卫星编号，造成基因编码无效的情况，本文采用等值压缩的方式解决该问题：
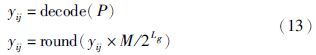
(3) 算法约束处理. 本文主要采用拒绝策略和修复策略. 当单个粒子元素不满足CCT约束时，用0替换该元素值，对粒子进行修复； 当粒子不满足CT、 CS约束时，采用拒绝策略，舍弃该粒子.
4 仿真结果分析本文仿真场景中，天基预警系统采用3×6的星座，包括3个轨道，每个轨道上均匀布防6颗卫星，卫星间隔60°，卫星高度1 600 km，轨道倾角85°. 卫星间通过60 GHz的星间链路进行数据传输，共享目标位置信息，完成对目标的接力跟踪.
根据式(9)和式(10)可知，当进行PSO更新策略时，采用整数编码，范围为0～18； 当进行GA相关操作时，采用二进制编码，范围是20160211～11111. 算法参数选取如下： 粒子个数为20，迭代次数为10； PSO中的c1=c2=1.494 45，最大速度的模为18，迭代次数为20； GA中的交叉概率为0.6，变异概率为0.01，迭代次数为20. 仿真的其它参数设置如表 1所示.
本文利用4.0 GB RAM的Inter(R)/3.20 GHz进行和仿真，以MATLAB R2013b为仿真环境. 为验证算法在各种负载情况下的性能，本文在10组场景下对文[8]的GASA、 文[9]的PSO、 GA及本文GA-PSO的算法进行20次蒙特卡洛测试，求取平均值. 目标数量从1个增加到70个，各个目标探测任务的优先级在(0，1)之间随机选取. 本文采用适应度函数值和任务完成率两类指标对仿真结果进行比较，任务完成率定义如下：
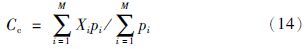
该指标能够综合反应出完成的任务数量及完成任务综合优先级.
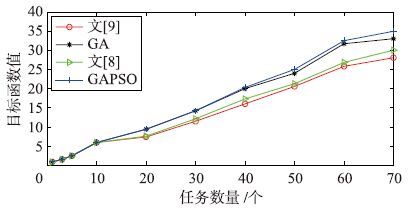
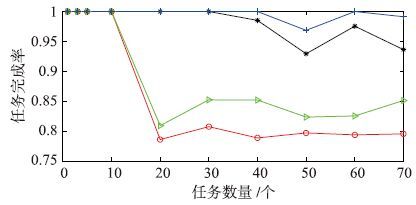
仿真结果如图 4和图 5所示. 从图 4中可看出，当目标数量较少时，文[8, 9]与本文的算法效果差距并不明显，此时系统探测资源充足，能够完成对所有目标的预警探测任务. 当目标超过20时，可较明显看出，文[8, 9]算法相较于另两类算法适应度函数值较小. 这主要是由于文[8]所运用的SA部分在规模较大时，一般只能得到近似解； 文[9]所用的PSO算法本身容易陷入局部最优值的缺陷造成的. 从任务完成率指标可以看出，GA-PSO算法由于结合了GA和PSO两种优化算法的优点，当目标数量增大时能够更多地完成目标探测任务.
|
| 图 4 适应度函数对比 Fig. 4 Comparison among fitness functions |
|
| 图 5 任务完成率对比 Fig. 5 Comparison of task completeness |
各算法在相同仿真场景中的运行时间如表 2所示，GA-PSO算法运行效率明显高于文[8]，这是由于文[8]在面对复杂调度系统时退火速度较慢； 但低于文[9]，对此可采用编译性语言和并行处理技术来进一步提高算法的实时性. 综合任务完成率分析，虽然文[9]运行效率较高，但当目标数超过20时，其任务完成率由1下降到0.8左右. 可根据实际情况，综合权衡效率和任务完成率选择具体的算法.
本文通过对天基预警卫星任务调度问题进行分析，采用一种融合GA和PSO的混合优化算法用于对卫星资源调度问题进行求解. 仿真结果表明本算法能够有效地提高搜索的效率，在相同情况下能够提高探测任务的完成率.
本文算法是建立在目标弹道可预知的前提下，并没有考虑目标运动的随机性. 后续研究拟结合滤波算法对目标轨迹进行实时修正，并将调度后结果反馈至信息融合模块，构成反馈融合系统.
| [1] | 刘波. 美国天基预警系统现状与发展[J]. 战术导弹术, 2011, 8(3): 118-123. Liu B. Status and development of American space-based early warning system[J]. Tactical Missile Technology, 2011, 8(3): 118-123. |
| [2] | 赵阳, 易先清, 罗雪山. 面向任务的天基预警系统应用体系结构研究[J]. 中国电子科学研究院学报, 2008(3): 247-251. Zhao Y, Yi X Q, Luo X S. Research on the application architecture of the space-based early warning system task-oriented[J]. Journal of China Academy of Electronics and Information Technology, 2008(3): 247-251. |
| [3] | 姜维, 李一军. 天基预警调度方法研究[J]. 系统工程理论与实践, 2012, 32(9): 2065-2077. Jiang W, Li Y J. The scheduling model and algorithm of space based early warning[J]. Systems Engineering - Theory & Practice, 2012, 32(9): 2065-2077. |
| [4] | 罗开平, 李一军. 导弹预警卫星调度问题分析[J]. 现代防御技术, 2009, 37(6): 5-10. Luo K P, Li Y J. Analysis of the early warning satellite scheduling problem[J]. Modern Defence Technology, 2009, 37(6): 5-10. |
| [5] | Sarkheyli A, Vaghei B G, Moghadam R A, et al. Scheduling earth observation activities in LEO satellites using graph coloring problem[C]//IEEE International Symposium on Telecommunications (IST). Piscataway, NJ, USA: IEEE, 2010: 928-931. |
| [6] | Wang H, Xu M, Wang R, et al. Scheduling earth observing satellites with hybrid ant colony optimization algorithm[C]//IEEE International Conference on Artificial Intelligence and Computational Intelligence. Piscataway, NJ, USA: IEEE, 2009: 245-249. |
| [7] | 阎志伟, 牛轶峰, 李汉铃. 基于并行禁忌遗传算法 (PTGA)的预警卫星传感器调度研究[J]. 宇航学报, 2003, 24(6): 598-603. Yan Z W, Niu Y F, Liu H L. Study of sensor scheduling for early warning satellite based on parallel tabu genetic algorithm (PTGA). Journal of Astronautics, 2003, 24(6): 598-603. |
| [8] | 郭浩波, 王颖龙, 曾辉. 采用遗传模拟退火算法研究弹预警卫星传感器调度[J]. 电光与控制, 2006, 13(4): 71-74. Guo H B, Wang Y L, Zeng H. Sensor scheduling for missile early-warning satellite based on genetic and simulated annealing algorithm[J]. Electronics Optics & Control, 2006, 13(4): 71-74. |
| [9] | 冯明月, 汤绍勋, 何俊, 等. 基于改进粒子群算法的天基预警系统资源调度方法[J]. 中国电子科学研究院学报, 2010, 5(1): 97-101. Feng M Y, Tang S X, He J, et al. Resource scheduling for space-based early warning system based on improved particle swarm optimization[J]. Journal of China Academy of Electronics and Information Technology, 2010, 5(1): 97-101. |
| [10] | 葛继科, 邱玉辉, 吴春明, 等. 遗传算法研究综述[J]. 计算机应用研究, 2008, 25(10): 2911-2916. Ge J K, Qiu Y H, Wu C M, et al. Summary of genetic algorithms research[J]. Application Research of Computers, 2008, 25(10): 2911-2916. |
| [11] | 马永杰, 云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012, 29(4): 1201-1206, 1210. Ma Y Z, Yun W X. Research progress of genetic algorithm[J]. Application Research of Computers, 2012, 29(4): 1201-1206, 1210. |
| [12] | 杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87-94. Yang W, Li Q Q. Particle swarm optimization algorithm[J]. Engineering Science, 2004, 6(5): 87-94. |
| [13] | 高卫峰, 刘三阳. 一种高效粒子群优化算法[J]. 控制与决策, 2011, 26(8): 1158-1162. Gao W F, Liu S Y. An efficient particle swarm optimization[J]. Control and Decision, 2011, 26(8): 1158-1162. |
| [14] | 贾树晋, 杜斌, 岳恒. 基于局部搜索与混合多样性策略的多目标粒子群算法[J]. 控制与决策, 2012, 27(6): 813-818. Jia S J, Du B, Yue H. Local search and hybrid diversity strategy based multi-objective particle swarm optimization algorithm[J]. Control and Decision, 2012, 27(6): 813-818. |
| [15] | 彭晓波, 桂卫华, 黄志武, 等. GAPSO: 一种高效的遗传粒子混合算法及其应用[J]. 系统仿真学报, 2008, 20(18): 5025-5027. Peng X B, Gui W H, Huang Z W, et al. GAPSO: Effective genetic particle swarm algorithm and its application[J]. Journal of System Simulation, 2008, 20(18): 5025-5027. |
| [16] | 栾丽君, 谭立静, 牛奔. 一种基于粒子群优化算法和差分进化算法的新型混合全局优化算法[J]. 信息与控制, 2007, 36(6): 708-714. Luan L J, Tan L J, Niu B. A novel hybrid global optimization algorithm based on particle swarm optimization and differential evolution[J]. Information and Control, 2007, 36(6): 708-714. |
| [17] | 宋晓宇, 王建国, 常春光. 基于需求紧迫度的非线性连续消耗应急调度模型与算法[J]. 信息与控制, 2014, 43(6): 735-743. Song X Y, Wang J G, Chang C G. Nonlinear continuous consumption emergency material dispatching model based on demand urgency degrees and its algorithm[J]. Information and Control, 2014, 43(6): 735-743. |
| [18] | 简平. 邹鹏. 熊伟. 基于DPSO-SA的低轨预警系统初始任务规划方法[J]. 北京航空航天大学学报, 2013, 39(10): 1381-1386. Jian P, Zou P, Xiong W. Original task planning method of early warning system of LEO based on DPSO-SA[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(10): 1381-1386. |
| [19] | 汤绍勋, 易先清, 罗雪山. 面向预警卫星调度问题的改进粒子群算法[J]. 系统工程, 2012, 30(1): 116-121. Tang S X, Yi X Q, Luo X S. An improved particle swarm optimization algorithm for early warning satellites scheduling problems[J]. Systems Engineering, 2012, 30(1): 116-121. |
| [20] | 张晓缋, 方浩, 戴冠中. 遗传算法的编码机制研究[J]. 信息与控制, 1997, 26(2): 55-60. Zhang X H, Fang H, Dai G Z. Studies on encoding mechanism of genetic algorithms[J]. Information and Control, 1997, 26(2): 55-60. |