2. 福建师范大学经济学院,福建 福州 350106;
3. 福建江夏学院电子信息科学学院,福建 福州 350008
2. School of Economics, Fujian Normal University, Fuzhou 350106, China;
3. School of Electronic Information Science, Fujianjiangxia University, Fuzhou 350008, China
匹配决策是指存在双方有限集合的主体,在已知信息下择优互选. 它最早源于Gale和Shapley提出的延迟接受算法[1]. 随后,许多学者从理论上完善、 扩展了该算法[2, 3, 4, 5],或从不同视角结合优化理论、 博弈论、 启发式算法等相关理论方法获取匹配结果. 作为机制设计理论[6]的重要内容,匹配决策存在大量实际应用背景,航天侦察任务与卫星资源匹配[7]、 如电子中介的交易匹配[8]、 风险投资商与投资企业互选[9, 10]、 虚拟企业伙伴选择问题[11]等.
主体双方在匹配过程中一般对潜在对象多个属性具有期望要求,多属性匹配决策(MAMDM)的研究已引起国内外学者们的关注[7, 8, 9, 10, 11, 12, 13, 14, 15]. 文[8]针对电子中介多属性商品交易问题,采用改进的模糊信息公理计算买卖双方的匹配度,提出基于Prüfer编码的多目标离散差分进化算法确定匹配结果. 文[9]提出了具有不同类型信息的风险投资商与投资企业的MAMDM问题,针对主体参照依赖和损失规避的特征,基于前景理论和TODIM法计算双方的总体感知价值,并以此最大化匹配互选. 文[12]针对信息系统外包中的MAMDM,通过构建评价指标体系,使用了层次分析法和PROMETHEE法的多准则决策方法进行匹配. 文[13]对带有主体期望值的无差异区间值MAMDM,提出一种基于前景理论的方法,以各指标期望值作为参照点,计算主体指标值相对于参照点的益损值构建前景矩阵,在此基础上进行双向择优互选. 文[14]等研究了不确定权重条件下的MAMDM,建立一种非线性优化模型确定主体的属性权重,然后根据得到双方主体满意度匹配信息,建立整数规划模型求解. 文[15]以主体对于各属性期望作为基准点,建立双方的损益矩阵和前景决策矩阵,并最大化双方的综合前景值获得匹配结果. 已有研究不仅丰富了MAMDM的相关理论方法,也扩大了其实际应用背景.
由于决策环境的复杂性、 信息不对称性及主体判断的模糊性,匹配中不免产生模糊不确定的匹配信息; 不仅包含对属性信息的不确定,也包含对属性权重信息的不确定. 自Atanassov[16, 17]在直觉模糊集(intuitionistic fuzzy set,IFS)基础上提出区间直觉模糊集(interval-valued intuitionistic fuzzy set,IVIFS)以来,众多学者在关于IVIFS的数学性质[18, 19]、 集成算子[19, 20, 21]、 一致性判断[22]、 相似性测度[22, 23]等方面取得了丰硕成果,并将其应用于模糊控制、 模式识别、 逻辑规划、 多属性决策等领域[19, 20, 21, 22, 23, 24]. MAMDM目前主要局限于匹配信息为偏序值、 精确数、 区间数或语言值,缺少对信息为IVIFS下的研究. IVIFS使用[0,1]区间数表示隶属度、 非隶属度和未知度,可细致地表达非此非彼的模糊概念,在描述、 处理不确定信息上具有很好的灵活性[25]. 因此,研究基于IVIFS的MAMDM问题,具有重要的学术价值和实际意义.
2 预备知识 2.1 区间直觉模糊集定义1[16, 17] 令X为非空论域,X上的区间直觉模糊集定义为:$\tilde F$ ={〈x,${\tilde u_{\tilde F}}$(x),${\tilde v_{\tilde F}}$(x)〉,x∈X},其中,${\tilde u_{\tilde F}}$(x)=[$u_{\tilde F}^L$(x),$u_{\tilde F}^U$(x)]⊂[0,1],${\tilde v_F}$(x)=[$v_{\tilde F}^L$(x),$v_{\tilde F}^U$(x)]⊂[0,1],分别表示x关于$\tilde F$的隶属度和非隶属度; 满足∃x∈X,0≤${\tilde u_{\tilde F}}$(x)+${\tilde v_{\tilde F}}$(x)≤1; 记${\tilde \pi _{\tilde F}}$(x)=[$\tilde \pi _{_{\tilde F}}^L$(x),$\tilde \pi _{_{\tilde F}}^U$(x)]=[1-$u_{\tilde F}^U$(x)-$v_{\tilde F}^U$(x),1-$u_{\tilde F}^L$(x)-u$u_{\tilde F}^L$(x)]⊂[0,1],表示x关于的未知度. 若$u_{\tilde F}^L$(x)=$u_{\tilde F}^U$(x),$v_{\tilde F}^L$(x)=$v_{\tilde F}^U$(x),则$\tilde F$退化为直觉模糊集F,即IFS是IVIFS的特殊情况.
一般将区间直觉模糊数(IVIFN)$\tilde f$简记为$\tilde f$=([uL,uU],[vL,vU]),其中[uL,uU],[vL,vU]⊂[0,1]; 规定$\tilde f$=([1,1],[1,0])为最大IVIFN,$\tilde f$=([0,0],[1,1])为最小区间直觉模糊数. 两个IVIFS之间存在多种形式的距离,如Hamming距离、 Euclidean距离等. 此外,文[25]定义了关于IFS的加权绝对值距离(weighted absolute distance,WAD),并可扩展到IVIFS的情形.
定义2[25] 非空论域X={x1,x2,…,xn},a={(xi,ua(xi),va(xi))|xi∈X},b={(xi,ub(xi),vb(xi))|xi∈X}为IFS,则a与b之间的WAD为

MAMDM涉及两方离散不相交的主体集合,设一方为A={A1,A2,…,Am},另一方为B={B1,B2,…,Bn}; 不失一般性,令m≤n. 其中,Ai(Bj)表示A(B)中第i(j)个主体,i=1,2,…,m,j=1,2,…,n; 约定各主体至多与一位潜在对象相匹配. A方主体属性集为D={d1,d2,…,dh},B方主体属性集为O={o1,o2,…,og},且D、 B均为加性独立.
定义3[2, 26] 匹配决策是集合A与B之间的一一映射μ: A∪B→A∪B,且满足:
(1) μ(Ai)∈B;
(2) μ(Bj)∈A∪{Bj};
(3) μ(Ai)=Bj当且仅当μ(Bj)=Ai.
定义4[2, 26] 若μ(Ai)=Bj,称(Ai,Bj)是μ确定的一个匹配对; 若μ(Ai)=Ai,则Ai在μ下未匹配; 由μ确定的匹配对集合称为一种匹配方案.
本文要解决的问题是: 根据给定的双方主体IVIFS的属性及属性权重信息及主体的匹配期望区间,确定一种尽可能使各双方满意的匹配方案.
3 多属性匹配决策方法 3.1 计算两个主体之间的匹配度双方主体匹配前,需要先计算各主体与潜在匹配对象之间的匹配度. 下文以主体Ai、 Bj为例进行讨论. 设专家给出Ai各属性d1,d2,…,dh评价值为([uipL,uipU],[vipL,vipU]),i=1,2,…,m,p=1,2,…,g,对应权重为Wi=([φA,iL,φA,iU],[φA,iL,φA,iU])1×h,i=1,2,…,m; 给出Bj各属性o1,o2,…,og评价值为([ujqL,ujqU],[vjqL,vjqU]),j=1,2,…,n,q=1,2,…,g,对应权重为Wj=([φB,jL,φB,jU],[φB,jL,φB,jU])1×g,j=1,2,…,n,则A方众主体评价信息可用矩阵表示为


一般而言,不同主体对于匹配对象有着不同的期望值,并用IFS表示; 令Ai对B方主体某属性oq的期望上、 下限值记为(ueiqU,veiqU)和(ueiqL,veiqL); 在主体理性情况下,可将最大直觉模糊数f=(1,0)作为主体的期望上限值,而期望下限值因主体而异.
考虑Ai与Bj的匹配度. 根据定义4,设d(Ai+,Bj)是Bj的各属性评价值与Ai的期望上限值的距离,则:

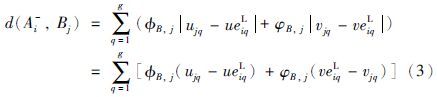
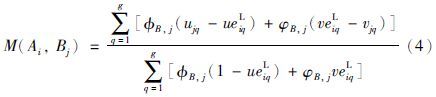

 >0,又φB,j,φB,j∈[0,1],即φB,j≥0,-φB,j≤0,则:
>0,又φB,j,φB,j∈[0,1],即φB,j≥0,-φB,j≤0,则:



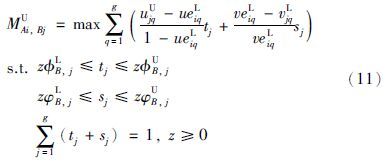

得到双方主体的匹配度矩阵后,引入0-1变量xij,i=1,2,…,m,j=1,2,…,n; xij=1表示Ai与Bj匹配,xij=0表示Ai与Bj未匹配. 以最大化各方匹配度之和为目标,建立如下的匹配决策模型(13):

不难看出,模型(13)为区间多目标指派问题模型,可将其改写为如下形式:


采用线性加权法[30]求解该模型. 令Zkmax(k=1,2,3,4)为模型(15)仅考虑各单目标函数时的最大值,相应地最优解为Xk*. 令Zkmin为仅考虑各单目标函数的最小值,Zkmin为



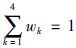 ; 权重wk可由专家给定或通过比较Zk的相对重要性来确定.
; 权重wk可由专家给定或通过比较Zk的相对重要性来确定.
定理1 模型(18)存在最优解.
证明 模型(18)为含有mn个变量的0-1线性规划模型,至多产生2mn个可行解; 即模型的可行域非空,因此其目标函数一定可以在可行域某个顶点达到最优,即模型(15)存在最优解,证毕.
定理2 模型(18)的最优解也是模型(15)的最优解.
证明 令模型(18)的最优解为x*,模型(15)的最优解为x′*且x′*≠x*,则对于模型(15)有Zk(x′*)≥Zk(x*),k=1,2,3,4. 又因为隶属度函数μzk(k=1,2,3,4)均为递增函数,即μzk(x*)≤μzk(x′*),这与题设x*为模型(18)最优解矛盾,故模型(15)和(18)最优解同解,证毕.
4 实例海西高新区有2家公司(A1,A2),各需选择1家匹配伙伴共同组建虚拟企业. 经信息发布,初步筛选,有5家潜在伙伴企业(B1,B2,…,B5)有合作意向; 由于双方缺乏前期基础,为达成匹配,管委会聘期专家、 企业顾问等人士对双方进行评价; 专家从企业规模(d1)、 管理能力(d2)、 项目回报率(d3)三方面评价A方; 专家从资源互补(o1)、 科技创新(o2)、 企业信誉(o3)三方面对B方进行评价. 具体的属性评价值见表 1、 2; 属性d1,d2,d3的权重依次为([0.41,0.68],[0.26,0.33]),([0.35,0.60],[0.32,0.40]),([0.39,0.70],[0.33,0.45]); 属性o1,o2,o3的权重为([0.28,0.56],[0.20,0.31]),([0.31,0.49],[0.21,0.34]),([0.35,0.45],[0.19,0.27]); 另外,各公司对潜在伙伴有一定期望要求,要求综合值不低于e-(表 3). 管委会以双方匹配度最大为准则拟定匹配方案.
| d1 | d2 | d3 | |
| A1 | ([0.45,0.68],[0.26,0.33]) | ([0.52,0.78],[0.22,0.40]) | ([0.71,0.89],[0.20,0.43]) |
| A2 | ([0.42,0.50],[0.30,0.45]) | ([0.66,0.84],[0.19,0.23]) | ([0.75,0.88],[0.18,0.38]) |
| o1 | o2 | o3 | |
| B1 | ([0.41,0.55],[0.39,0.54]) | ([0.75,0.90],[0.22,0.40]) | ([0.84,0.91],[0.27,0.40]) |
| B2 | ([0.53,0.77],[0.25,0.45]) | ([0.66,0.85],[0.29,0.44]) | ([0.78,0.85],[0.18,0.35]) |
| B3 | ([0.48,0.78],[0.25,0.50]) | ([0.65,0.81],[0.34,0.58]) | ([0.82,0.89],[0.10,0.33]) |
| B4 | ([0.50,0.84],[0.30,0.35]) | ([0.53,0.71],[0.32,0.51]) | ([0.75,0.90],[0.25,0.29]) |
| B5 | ([0.39,0.56],[0.20,0.33]) | ([0.77,0.91],[0.28,0.43]) | ([0.68,0.77],[0.30,0.49]) |
| o1 | o2 | o3 | d1 | d2 | d3 | ||
| B1 | (0.30,0.65) | (0.38,0.67) | (0.28,0.77) | ||||
| A1 | (0.30,0.70) | (0.31,0.68) | (0.35,0.65) | B2 | (0.35,0.71) | (0.28,0.65) | (0.32,0.64) |
| B3 | (0.24,0.69) | (0.30,0.73) | (0.20,0.73) | ||||
| A2 | (0.27,0.63) | (0.35,0.60) | (0.32,0.71) | B4 | (0.31,0.60) | (0.35,0.65) | (0.29,0.62) |
| B5 | (0.38,0.61) | (0.33,0.60) | (0.30,0.69) |
首先,由式(2)、 (3)计算各主体到潜在匹配对象的期望距离,再根据式(11)及式(12)得到双方两两主体之间的匹配度矩阵,计算结果如表 4、 5所示.
| 主体 | 匹配对象 | ||||
| B1 | B2 | B3 | B4 | B5 | |
| A1 | [0.620,1.540] | [0.659,1.510] | [0.717,1.639] | [0.652,1.447] | [0.685,1.567] |
| A2 | [0.714,1.479] | [0.649,1.467] | [0.490,1.593] | [0.775,1.397] | [0.881,1.508] |
| 潜在对象 | 主体 | ||||
| B1 | B2 | B3 | B4 | B5 | |
| A1 | [1.057,1.840] | [1.144,1.963] | [1.040,1.998] | [1.011,1.914] | [0.983,1.769] |
| A2 | [1.137,1.966] | [1.210,2.090] | [1.108,2.219] | [1.079,2.043] | [1.066,1.876] |
再根据式(15)~(16),依次求解各单目标函数Zkmin、 Zkmax及最优解Xk*(表 6),进而,依据式(17)计算各单目标函数的隶属度; 令双方在匹配过程中的地位相等且双方的区间匹配度左右端点权重也相等,即w1=w2=w3=w4=0.25. 最后得到的最优解为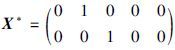 即最优匹配方案为A1↔B2,A2↔B3.
即最优匹配方案为A1↔B2,A2↔B3.
| k=1 | k=2 | k=3 | k=4 | |
| Zkmin | 1.149 | 2.989 | 2.091 | 4.182 |
| Zkmax | 1.598 | 3.160 | 2.281 | 3.874 |
| Xk* | (1,3),(2,5) | (1,5),(2,3) | (1,2),(2,1) | (1,2),(2,3) |
本文给出了基于区间直觉模糊集的多属性匹配决策方法,在属性及属性权重均为不确定信息下的匹配决策提供一种解决途径. 该方法以一方主体的匹配期望值作为参考点,依据TOPSIS的思想计算它与另一方潜在对象的加权距离,并依此作为两者之间的匹配度; 在此基础上以双方匹配度最大为目标,构建区间双目标优化模型并转化、 求解模型得到最优匹配结果. 最后通过区间直觉模糊信息下,组建虚拟企业的盟员双向选择问题验证所提方法的有效性.
与已有文献相比,本文方法的创新点主要体现在:
(1) 文[9, 11, 12, 13, 14, 15]研究了属性为精确数、 区间数、 语言值或三角模糊数的决策情形,且属性权重为精确值的MAMDM问题,本文主要研究属性和权重均为IVIFN的匹配决策问题,研究对象所有不同.
(2) 在文[26]所建模型基础上,拓展到匹配决策中含有区间数的情形; 同时,采用隶属函数加权法将原模型转为单目标线性模型求解,得到最优匹配方案.
(3) 文[7, 8]所建立的匹配模型为非线性的,采用启发式和离散差分算法求解,过程复杂运算量大; 本文建立的所有模型,通过变换均可转化为线性优化模型,并采用基于隶属度函数的线性加权法求解,较为简便.
综上,本文方法具有较好的理论支撑且计算量小,可为实际多属性匹配决策问题提供理论参考.
| [1] | Gale D, Shapley L S. College admissions and the stability of marriage[J]. American Mathematical Monthly, 1962, 69(1): 9-15. |
| [2] | Roth A E. Common and conflicting interests in two-sided matching markets[J]. European Economic Review, 1985, 27(1): 75-96. |
| [3] | Roth A E, Rothblum U G, Vate J H. Stable matchings, optimal assignments, and linear programming[J]. Mathematics of Operations Research, 1993, 18(4): 803-828. |
| [4] | Erdil A, Ergin H. What's the matter with tie-breaking? Improving efficiency in school choice[J]. American Economics Review, 2007, 98(3): 669-689. |
| [5] | Teo C P, Sethuraman J, Tan W P. Gale-shapley stable marriage problem revisited: Strategic issues and applications[J]. Management Science, 2001, 47(9): 1252-1267. |
| [6] | Hurwicz L, Reiter S. Designing economic mechanisms[M]. Cambridge, UK: Cambridge University Press, 2006. |
| [7] | 谈群, 彭黎, 李志猛等. 一种航天侦察任务——资源匹配的负载均衡方法[J]. 国防科技大学学报, 2011, 33(2): 95-99. Tan Q, Peng L, Li Z, et. al. A load balancing method for matching reconnaissance tasks and satellite resources[J]. Journal of National University of Defense Technology, 2011, 33(2): 95-99. |
| [8] | 蒋忠中, 樊治平. 具模糊信息的多数量多属性电子交易匹配问题[J]. 管理科学学报, 2014, 17(5): 52-65. Jiang Z Z, Fan Z P. Matching model and algorithm for multi-unit mufti-attribute exchanges with fuzzy information in E-brokerage[J]. Journal of management science in China, 2014, 17(5): 52-65. |
| [9] | 万树平, 李登峰. 具有不同类型信息的风险投资商与投资企业多指标双边匹配决策方法[J]. 中国管理科学, 2014, 22(2): 40-47.Wan S H, Li D F. Decision making method for multi-attribute two-sided matching problem between venture capitalists and investment enterprises with different kinds of information[J]. Chinese Journal of Management Science, 2014, 22(2): 40-47. |
| [10] | Elitzur R, Gavious A. A multi-period game theoretic model of venture capitalists and entrepreneurs[J]. European Journal of Operational Research, 2003, 144(2): 440-453. |
| [11] | Huang B, Gao C, Chen L. Partner selection in a virtual enterprise under uncertain information about candidates[J]. Expert Systems with Applications, 2011, 38(9): 11305-11310. |
| [12] | Wang J J, Yang D L. Using a hybrid multi-criteria decision aid method for information systems outsourcing[J]. Computers & Operations Research, 2007, 34(12): 3691-3700. |
| [13] | 乐琦. 基于前景理论的相同无差异区间型多指标匹配决策方法[J]. 系统科学与数学, 2013, 33(12): 1447-1455. Yue Q. The same indifference interval multiple criteria matching decision method based on prospect theory[J]. Journal of Systems Science andMathematical Sciences, 2013, 33(12): 1447-1455. |
| [14] | Zhang Z, Guo C H. A hybrid multiple attributes two-sided matching decision making method with incomplete weight information[M]. Berlin: Springer Berlin Heidelberg, 2011: 272-283. |
| [15] | 陈希, 韩菁, 张晓. 考虑心理期望与感知的多属性匹配决策方法[J]. 控制与决策, 2014, 29(11): 2027-2033ChenX, HanJ, ZhangX. Method for multiple attribute matching decision making considering matching body's psychological aspirationandperception[J]. Control and Decision, 2014, 29(11): 2027-2033. |
| [16] | Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy sets and Systems, 1986, 20(1): 87-96. |
| [17] | Atanassov K, Gargov G. Interval valued intuitionistic fuzzy sets[J]. Fuzzy sets and systems, 1989, 31(3): 343-349. |
| [18] | Deschrijver G, Kerre E E. On the composition of intuitionistic fuzzy relations [J]. Fuzzy Sets and Systems, 2003, 136(3): 333-361. |
| [19] | Xu Z, Yager R R. Some geometric aggregation operators based on intuitionistic fuzzy sets[J]. International journal of general systems, 2006, 35(4): 417-433. |
| [20] | Xu Z. Intuitionistic fuzzy aggregation operators[J]. IEEE Transactions on Fuzzy Systems, 2007, 15(6): 1179-1187. |
| [21] | Liu P. Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(1): 83-97. |
| [22] | Wang Z J. Derivation of intuitionistic fuzzy weights based on intuitionistic fuzzy preference relations[J]. Applied Mathematical Modeling, 2013, 37(9): 6377-6388. |
| [23] | Xu Z, Xia M. Distance and similarity measures for hesitant fuzzy sets[J]. Information Sciences, 2011, 181(11): 2128-2138. |
| [24] | 赖于树, 熊燕, 刘毓. 规则优先权排序的直觉模糊群决策算法[J]. 信息与控制, 2013, 42(3): 314-319. Lai Y S, Xiong Y, Liu Y. Intuitionistic fuzzy group decision making algorithm for rule priority ranking[J]. Information and Control, 2013, 42(3): 314-319. |
| [25] | Li D F. Linear programming method for MADM with interval-valued intuitionistic fuzzy sets[J]. Expert Systems with Applications, 2010, 37(8): 5939-5945. |
| [26] | 樊治平, 李铭洋. 考虑稳定匹配条件的双边满意匹配决策方法[J]. 中国管理科学, 2009.22(4), 113-118. Fan Z P, Li M Y. Decision analysis method for two-sided satisfied matching considering stable matching condition[J]. Chinese Journal of Management Science, 2009, 22(4): 113-118. |
| [27] | Chen C T. Extensions of the TOPSIS for group decision-making under fuzzy environment[J]. Fuzzy sets and systems, 2000, 114(1): 1-9. |
| [28] | Wang Y M, Chin K S, Luo Y. Cross-efficiency evaluation based on ideal and anti-ideal decision making units[J]. Expert Systems with Applications, 2011, 38(8): 10312-10319. |
| [29] | 刘洋, 樊治平. 一种具有区间数信息的多目标指派方法[J]. 运筹与管理, 2007, 16(5): 17-22. |
| [30] | Oliveira C, Antunes C H. Multiple objective linear programming models with interval coefficientsan illustrated overview[J]. European Journal of Operational Research, 2007, 181(3): 1434-1463. |



