传统PID控制器由于其结构简单、 物理意义明确、 控制效果及稳定性好等优点被广泛的应用于工业控制的各个领域,如冶金、 机械、 电力、 化工等[1, 2, 3]. 但随着控制水平的不断提高,人们对控制精度、 抗干扰能力及系统鲁棒性提出了更高的要求,常规PID控制难以获得满意的效果. Podlubny在总结前人经验的基础上提出了分数阶PID控制器[4],其一般格式记为PIαDβ. 分数阶PIαDβ控制器与传统PID控制器相比,多了两个可调参数(α,β). 当α=β=1时,控制器属于常规PID控制器,正是由于α、 β连续可调,因此分数阶PIαDβ控制器具有更大的调节范围、 更强的鲁棒性,为得到更优的系统动态性能创造了条件[5, 6]. 虽然分数阶PIαDβ控制器具有良好的控制效果,但是目前主流的分数阶控制器参数整定方法都有计算量大且复杂、 待求解参数多等缺点,往往需要与模糊控制、 神经网络、 遗传算法等[7, 8, 9]智能算法相结合来克服分数阶控制器参数整定的复杂性. 内模控制[10]是基于数学过程模型进行控制器设计的新型控制方法,具有结构简单、 在线调节参数少、 鲁棒性强等优点,从而使其在工业控制中得到广泛应用. 将内模控制与分数阶控制理论相结合,可以有效克服分数阶控制器参数整定复杂、 计算量大等缺点,并能改善系统控制性能[11, 12]. 文[11]提出的基于控制系统期望带宽的内模分数阶PID控制器,需要分析系统的频率响应特性,而文[12]是利用滤波器参数与最大灵敏度之间的关系来设计分数阶内模控制器的,但未给出二者通用的关系表达式.
对于分数阶控制系统,传统的方法是将其近似为整数阶系统,然后对近似系统进行控制器设计[13, 14, 15],这样就存在设计偏差甚至不能满足系统稳定性要求. 本文将内模控制思想引入到分数阶控制器参数整定中,提出一种分数阶内模TIλDμ控制器设计方法,所提新型TIλDμ控制器的实现克服了以往分数阶PID控制器参数整定的复杂性,改善了系统的控制性能,仿真结果表明了所提方法的有效性.
2 内模控制内模控制的基本思路[10]是将实际对象与对象模型相并联,控制器取模型的动态逆,从而满足闭环系统性能,并通过添加低通滤波器来增强系统的鲁棒性.
2.1 内模控制结构内模控制的基本结构如图 1所示,R(S)为参考轨迹即设定值,Y(S)为系统的输出,D(S)是外来扰动,G(S)与M(S)分别对应实际被控对象模型和内模被控对象模型.

|
| 图 1 内模控制框图 Fig. 1 The block diagram of IMC |
在传统反馈控制中,反馈控制器GIMC(s)可通过内模结构中C(s)与M(s)结合而成:
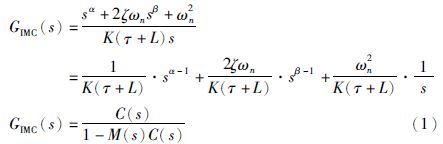
模型分解:
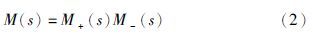
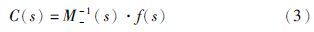
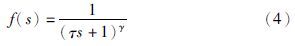
Lune于1994年申请了“three-parameter tunable tilt-integral derivative (TID) controller”发明专利[16]. 在该专利中,Lune对PID控制器进行了结构上的改进,改进后的PID控制器用分数阶环节s-1n取代了比例环节,从而得到了TID控制器. 实际上这也是分数阶PIαDβ控制器的一种特殊形式. TID控制器具有抗干扰、 其闭环对参数变化不敏感等特点,但其参数整定方法仍需讨论和检验[17]. 本文在TID控制器的结构上作了改进,不仅用分数阶环节取代比例环节,同时也用分数阶环节取代微分、 积分环节,得到分数阶TIλDμ. 该控制器的传递函数可表示为
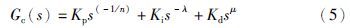
本文根据文[18]的模型降阶方法,采用2阶非整数阶延时系统做为优化参数模型结构,即:
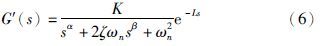

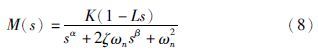
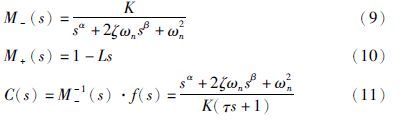
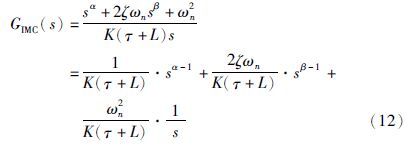
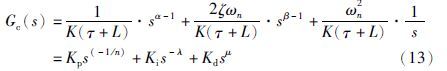
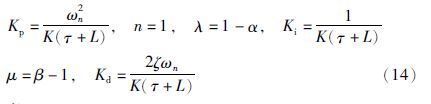
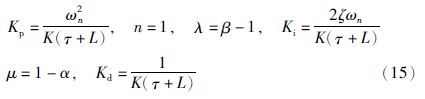
例1 文[15]给出一个加热炉的整数阶模型:
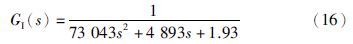
针对式(16),文[18]给出的2阶分数阶延时系统降阶模型:
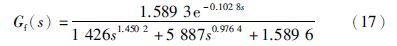
由式(17)可得: 2ζω=5 887/1 426,ω2n=1.589 3/1 426,L=0.102 8,α=1.450 2,β=0.976 4.
将上述参数代入到式(14)或式(15)可得
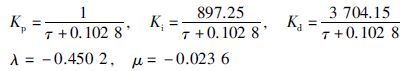
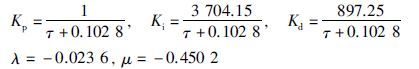
因此得到分数阶内模TIλDμ:
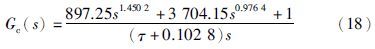
下面通过调节滤波器参数τ(τ=0.001,0.01,0.5,1,5,10),获得一组如下控制器形式:

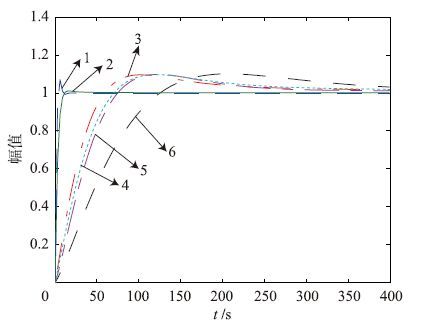
采用式(19)~(24)控制器分别对加热炉模型(16)进行闭环单位阶跃测试,得到系统仿真对比图,如图 2所示.
|
| 图 2 系统单位阶跃响应对比 Fig. 2 Comparisonof the unit step responseof the system |
图中曲线1~6分别表示滤波器参数τ由0.001增至10时对应的闭环系统单位阶跃曲线. 由图 2可以看出,当滤波器参数由小变大时,系统上升时间逐渐增大,当τ=0.01时对应的是曲线2,相比较而言τ=0.01可以获得比较满意的控制效果,此时对应的分数阶内模TIλDμ控制器为
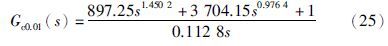
文[15]针对式(16)给出了整数阶PID控制器为
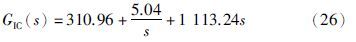
文[18]针对式(17)给出了最优分数阶PID控制器为
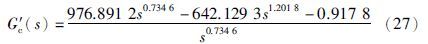
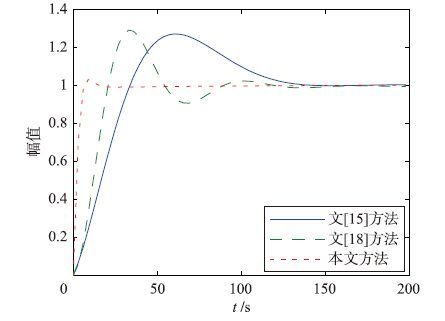
分别采用本文方法与文[15]、 文[18]方法得到系统的单位阶跃响应如图 3所示. 从图 3的阶跃响应对比可得,本文设计的分数阶内模TIλDμ控制器无论是在上升时间、 调节时间、 超调量均具有优越性.
|
| 图 3 不同控制作用下系统单位阶跃响应对比 Fig. 3 Comparison of the unit step response of the system with different controllers |
当被控系统参数发生变化时,即加热炉整数阶模型(16)变形,如式(28)所示:
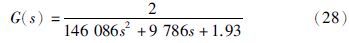
针对式(28),分别采用式(25)~(27)控制器进行闭环控制,得到的系统单位阶跃响应如图 4所示.

|
| 图 4 模型失配时的系统单位阶跃响应对比 Fig. 4 Comparison of the unite step response of the system within a mismatch model |
为了有效地说明分数阶内模TIλDμ控制器具有更好的控制品质和鲁棒性,本文选取闭环系统的超调量δ%、 绝对时间误差积分ITAE作为验证系统控制品质的指标,如表 1所示. 由图 3、 图 4和表 1可得,本文所提分数阶内模TIλDμ控制器控制品质和鲁棒性更好.
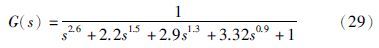
针对式(29),文[18]给出的二阶分数阶延时系统模型:
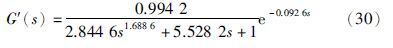
由式(30)可得K=0.994 2/2.844 6,2ζωn=5.528 2/2.844 6,ω2n=1/2.844 6,L=0.092 6,α=1.688 6,β=1. 同样按照上述滤波器参数选取方法,最终取τ=0.01系统能够获得比较满意的控制效果. 将参数代入到式(14)、 (15)得
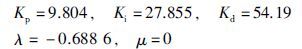
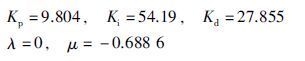
因此得到分数阶TIλDμ控制器:
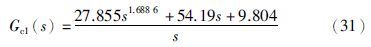
文[18]针对式(30)给出了最优分数阶PID控制器:
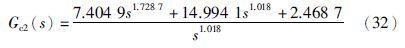
文[19]针对式(30)给出的一种分数阶内模PID控制器:
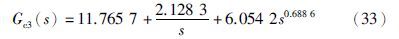
文[20]针对式(29)给出的一种分数阶内模PID控制器:
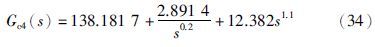
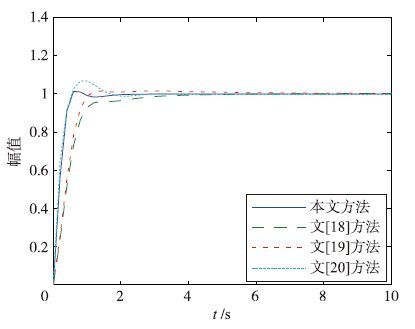
分别采用本文方法、 文[18, 19, 20]方法得到系统的单位阶跃响应如图 5所示.
|
| 图 5 分数阶被控系统单位阶跃响应对比 Fig. 5 Comparison of the unit step responseof a fractional-order system |
从图 5可得,与文[18, 19, 20]所提控制器相比,本文设计的分数阶内模TIλDμ控制器上升时间短、 稳态误差小、 存在微小超调,控制器具有良好的控制品质.
当系统参数发生变化时,即:
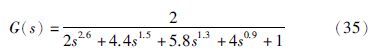
其系统单位阶跃响应如图 6所示. 从图 5、 6和表 2可得,本文方法与文[18, 19, 20]方法相比,都存在微小超调. 综合考虑,本文所提控制器在动态响应和鲁棒性方面均具有一定优势.

|
| 图 6 模型失配时分数阶被控系统的单位阶跃响应对比 Fig. 6 Comparison of the unit step responseof fractional-order system within a mismatch model |
本文分别针对整数阶与分数阶被控对象,提出一种分数阶内模TIλDμ控制器,阐述了所提新型控制器的设计思想. 所提新型控制器在被控对象模型降阶的基础上实现参数的快速整定,因此在一定程度上克服了以往分数阶控制器参数整定复杂的问题. 最后通过实例仿真与数据对比,得出所提新型控制器在系统动态响应和鲁棒性方面较文献中所提方法均具有一定优势. 但是,本文所提新型控制器仅处于仿真基础上,对于如何将该控制器运用于实际系统并满足系统实时性要求还有待于进一步研究.
| [1] | 黄茹楠, 观晴晴, 高英杰, 等. 电机振动台的模糊PID控制的研究[J]. 液压与气动, 2009(4): 36-38. Huang R L, Guan Q Q, Gao Y J, et al. The study of fuzzy PID control for motor vibration table[J]. Hydraulic and Pneumatic, 2009(4): 36-38. |
| [2] | 李亮, 康铭鑫, 宋健, 等. 汽车牵引力控制系统的变参数自适应PID控制[J]. 机械工程学报, 2011, 47(12): 92-98. Li L, Kang M X, Song J, et al. Parameters adaptive variable of PID control for traction control system[J]. Mechanical Engineering, 2011, 47(12): 92-98. |
| [3] | 彭勇刚, 韦巍. 注塑机机械手位置伺服系统灰色预测及迭代学习混合控制[J]. 仪器仪表学报, 2008, 29(10): 2062-2066. Peng Y G, Wei W. Gray prediction and iterative learning control for the position servo system of the injection molding machine manipulator[J]. Chinese Journal of Scientific Instrument, 2008, 29(10): 2062-2066. |
| [4] | Podlubny I. Fractional-order systems and PI D-controllers[J]. IEEE Transactions on Automatic Control, 1999, 64(8): 1287-1300. |
| [5] | Sadati N, Ghaffarkhah A, Ostadabbas S. A new neural network based FOPID controller[C]//IEEE International Conference on Networking, Sensing and Control. Piscataway, NJ, USA: IEEE, 2008: 762-767. |
| [6] | Caponetto R, Fortuna L, Porto D. A new tuning strategy for a non integer order PID controller[C]//First IFAC workshop on fractional differentiation and its application. 2004: 168-173. |
| [7] | 曹军义, 梁晋, 曹秉刚. 基于分数阶微积分的模糊分数阶控制器研究[J]. 西安交通大学学报, 2005, 39(11): 1246-1253. Cao J Y, Liang J, Cao B G. Study on fuzzy fractional-order controller based on fractional calculus[J]. Academic Journal of Xi'an Jiaotong University, 2005, 39(11): 1246-1253. |
| [8] | 赵慧敏, 李文, 邓武. 基于神经网络的分数阶PIα控制器的设计与实现[J]. 大连交通大学学报, 2008, 28(1): 63-67. Zhao H M, Li W, Deng W. Design and Implementation of fractional-order PIα controller based on neural network[J]. Journal of Dalian Jiaotong University, 2008, 28(1): 63-67. |
| [9] | 李大宇, 刘展, 靳其兵, 等. 基于遗传算法的分数阶控制器参数整定研究[J]. 控制工程, 2006, 13(4): 384-387. Li D Z, Liu Z, Z Q B, et al. Research on the parameters set of fractional-order controller based on genetic algorithm[J]. Control Engineering of China, 2006, 13(4): 384-387. |
| [10] | 文新宇, 张井岗, 王建国. 多模型内模PID控制[J]. 太原科技大学学报, 2007, 28(4): 270-273. Wen X Y, Zhang J G, Wang J G. Multi-model internal model PID control[J]. Academic Journal of Taiyuan University of Science and Technology, 2007, 28(4): 270-273. |
| [11] | Vinopraba T, Sivakumaran N, Narayanan S, et al. Designof internal model control basedfractional order PIDcontroller[J]. Control Theory andApplications, 2012, 10(3): 297-302. |
| [12] | Tavakoli-Kakhki M, Haeri M. Fractional order model reduction approach based on retention of the dominant dynamics: Application in IMC based tuning of FOPI and FOPID controllers[J]. ISA transactions, 2011, 50(3): 432-442. |
| [13] | Bhaskaran T, Chen Y Q, Xue D. Practical tuning of fractional order proportional and integral controller (i): Tuning rule development[C]//ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York, NY, USA: American Society of Mechanical Engineers, 2007: 1245-1258. |
| [14] | Wang J F, Li Y K. Frequency domain stability criteria for fractional-order control systems[J]. Journal of Chongqing University, 2006, 1(1): 30-35. |
| [15] | 薛定宇, 赵春娜. 分数阶系统的分数阶PID控制器设计[J]. 控制理论与应用, 2007, 24(5): 771-776. Xue D Y, Zhao C N. Fractional-order PID controller design for the fractional-order system[J] Control Theory & Applications, 2007, 24(5): 771-776. |
| [16] | Lurie B J. Three-parameter tunable tilt-integral-derivative (TID) controller: U. S. Patent 5, 371, 670[P]. 1994-12-6. |
| [17] | Xue D Y, Chen Y Q. A comparative introduction of four fractional order controllers[C]//Proceedings of the 4th World Congress on Intelligent Control and Automation. Piscataway, NJ, USA: IEEE, 2002: 3228-3235. |
| [18] | 肖培智, 林青松, 徐兴元, 等. 基于模型降阶的分数阶系统动态性能研究[J]. 计算机仿真, 2014, 31(8): 273-277. Xiao P Z, Lin Q S, Xu X Y. Study on dynamic performance of model reduction based on the fractional-order system[J]. Computer Simulation, 2014, 31(8): 273-277. |
| [19] | 赵志诚, 张博, 刘志远, 等. 一种分数阶系统内模PID控制器设计方法[J]. 信息与控制, 2014, 43(2): 129-133. Zhao Z C, Zhang B, Liu Z Y, et al. A design method of IMC-PID controller for the fractional-order system[J]. Information and Control, 2014, 43(2): 129-133. |
| [20] | 李大字, 刘展, 曹娇. 基于IMC方法的分数阶系统控制器设计[C]//2007仪表自动化及先进集成技术大会论文集. 北京: 仪器仪表学报, 2007: 362-365. Li D Z, Liu Z, Cao J. Fractional-order system controller design based on IMC method[C]//2007 Instrument Automation and Integration of Advanced Technology Conference Proceedings. Beijing: Chinese Journal of Scientific Instrument, 2007: 362-365. |



