2. 武汉理工大学自动化学院,湖北 武汉 430070
2. School of Automation, Wuhan University of Technology, Wuhan 430070, China
时滞系统的控制问题[1]一直是工程实践中的难点,其广泛存在于苛化工段生产过程[2]、 生物发酵、 炉温控制系统[3]、 中央空调控制系统[4]等方面. 相对于稳定的时滞系统,不稳定的时滞系统由于存在不稳定环节,故实现其优化控制存在着更大的困难.
近年来,学者们针对二阶不稳定时滞过程(unstable second order process with time delay,USOPTD)作了大量研究. PID控制作为一种最基本的控制策略,可靠性强且具有较好的鲁棒性,因而在工程实践中得到了广泛应用,开发出了各种改进型PID控制器[5, 6, 7, 8, 9, 10, 11, 12, 13, 14]. 其中文[14]采用基于IMC(internal model control)的PID控制器,并串入前置滤波器的方法,对负荷扰动的控制效果较好,但在参数扰动下,系统抗扰动鲁棒性并不十分理想. 由于PID和各种改进型PID控制器都只有2维3参数,构不成无穷维的观察器和控制器,因此它们不能实现时滞系统的最优控制; 为了消除时滞,人们开发出了Smith预估器及各种改进型Smith预估器[15, 16]. 当全补偿时,其控制效果明显; 当出现欠补偿或者过补偿时,控制系统中就会出现超前项和滞后项,性能指标必然急剧恶化. 项国波等[18, 19, 20, 21, 22, 23]提出二次优化控制(twice optimal control,TOC)的方法,实现了稳定时滞系统的优化控制,并将其应用于皮带秤和稠油热采锅炉蒸汽干度控制系统中,实现了跟踪控制快速平稳、 抗扰控制鲁棒性强的性能指标,但尚未解决不稳定时滞过程的优化控制问题. 文[24]采用内部比例反馈,使不稳定极点对称配置,构成广义的一阶稳定对象,再运用二次优化控制方法,实现了被控对象的鲁棒控制,具有较好的跟踪响应性能,但对二阶甚至高阶不稳定时滞系统未有进一步或更深入的研究.
本文将文[18]中的二次优化控制的方法应用到一类二阶不稳定时滞系统上,针对其过渡过程中出现的微振现象,提出采用增强局部反馈Kf的结构整形方法来获得更好的控制效果. 仿真实验结果表明: 整形后的二次优化控制方法跟踪响应更加快速平稳,抗扰控制鲁棒性几近无穷大. 最后与文[14]和文[16]所提出的方法,分别在参数扰动和负载扰动下做对比研究,通过仿真实例证明了本文在动态性能和抗扰动性能方面的优越性.
2 二次优化控制器设计原理设二阶纯时滞过程数学模型为

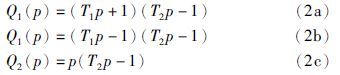
为实现式(1)的优化控制,把无穷维因子表示成:
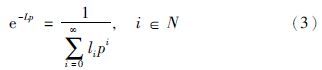

文[18, 19, 20, 21, 22, 23]采用μ阶分时模型逼近式(3)中的无穷维因子e-Lp得到其有穷维数学模型,如式(5)所示:

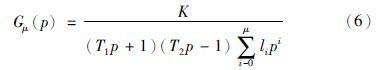
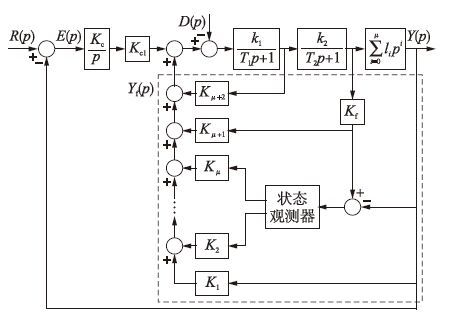
根据文[18]给出的二次优化控制原理,式(6)被控对象的二次优化控制结构图如图 1所示,其中K1、 K2、 …Kμ+2为反馈系数,Kc为被控对象的放大系数.

|
| 图 1 式(2a)所示的μ阶USOPTD二次优化控制结构图 Fig. 1 The TOC structure diagram of μ order USOPTD process such as Eq.(2a) |
图 1中状态观测器部分如图 2所示,对应其状态方程如式(7)所示:

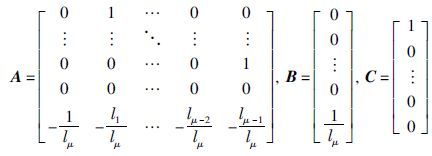
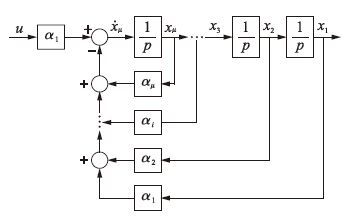
|
| 图 2 μ阶时滞项观测器 Fig. 2 State observer for μ order time-delay term |
根据式(7),构造μ维状态控制器,如式(8)所示:
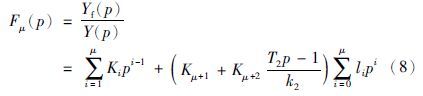
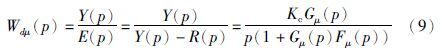
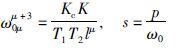
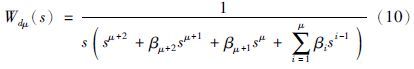
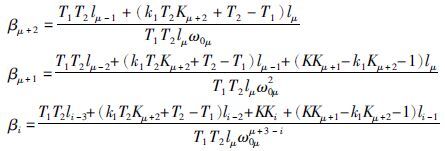
选定超调量σ1%后,从文[18]便可查阅与s同一阶幂的X-Y型位移无静差开环ITAE (integral time absolute error)最优传递函数系数集{βi},便得到式(11)中的优化控制器参数集:
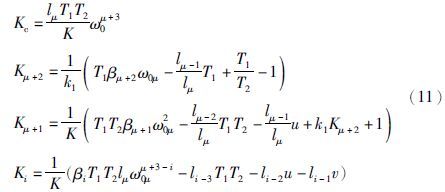
式(11)中Kμ+1和Kμ+2两算式,不同于稳定时滞系统控制器参数,它意味着先用局部负反馈,将不稳定环节镇定,然后才能将其改造为最优控制系统.
应该指出,当i<0时,式(11)中li=0. 由于己选取了标准型系数集{βi},故式(11)中未知量只有ω0μ. 为实现二次优化控制,需要用无穷维因子e-Lp取代图 1中的μ阶分时模型,此时系统的状态反馈方程如式(12)所示:
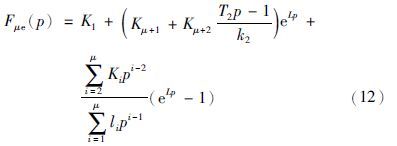
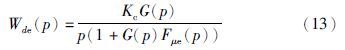
例设被控对象为
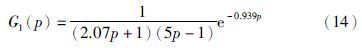
为了确定式(14)被控对象的二次优化控制器参数,分别取μ=1,2,3,选定σ1%=1%,文[18]中X-Y-Ⅲ型标准系数集如表 1所示.
| β1 | β2 | β3 | β4 | β5 | |
| μ=1 | — | — | 2.161 | 3.440 | 2.758 |
| μ=2 | — | 2.625 | 4.818 | 5.270 | 3.399 |
| μ=3 | 3.096 | 6.494 | 8.670 | 7.576 | 4.065 |
通过计算机仿真,寻求最优参数ω0μ,将其代入式(11),便得二次优化控制参数如表 2所示.
| K5 | K4 | K3 | K2 | K1 | Kc | |
| ω01=0.772 | — | — | 0.663 | 16.232 | -2.237 | 3.452 |
| ω02=1.126 | — | 1.186 | 23.058 | 5.896 | 4.059 | 8.259 |
| ω03=1.582 | 2.939 | 45.463 | 3.819 | 11.155 | 16.004 | 22.389 |
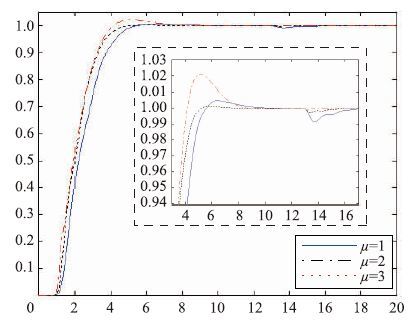
当t=20 s时,突加-0.2的负荷扰动,其系统阶跃响应曲线如图 3所示,幅相频率特性示如图 4所示. 它们的品质指标汇于表 3所示,表中Edm/%为突加负荷后的输出最大跌落,tsd为负荷扰动恢复到误差允许范围内的时间; 调节时间ts以2%的误差为准.
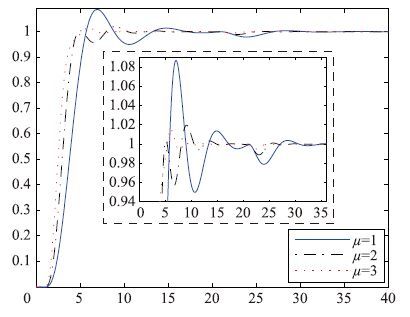
|
| 图 3 负载扰动为-0.2时的阶跃响应曲线 Fig. 3 Step response curve when -20% load disturbance occurs |

|
| 图 4 二次优化控制系统的Nyquist图 Fig. 4 Nyquist diagram of USOPTD system |
| Σ /% | ts | Edm/% | tsd | |
| μ=1 | 9.06 | 5.4 | -2.01 | 5.3 |
| μ=2 | 4.3 | 4.5 | -1.22 | 1.5 |
| μ=3 | 1.2 | 4.7 | -0.5 | 1.1 |
上述结果表明: 二次优化控制系统基本上消除了时滞因子,因此抗负荷能力强; 而且分时模型的阶次愈高,跟踪响应愈快速、 超调愈小、 抗负荷扰动愈强. 图 4指出,3个不同分时模型的二次优化控制系统,它们的相角裕量相差不大且都大于60°,但幅值裕量相差很大. 当μ=1时,系统幅值裕量最小,所以它的超调最大; 当μ=3时,系统幅裕量最大,所以它的超调最小.
3 二次优化控制的结构整形上述被控对象3个不同分时模型的优化控制系统有一个共同点: 上升过程都快速平稳,但在趋于稳态前都呈微幅收敛性振荡,这种特性降低了它的抗扰能力,因此需要对它进行结构整形,进一步提高它的鲁捧性.
经分析: 这种微幅振荡是由于系统开环频率特性的中频段阻尼不足造成的,因此结构整形的有效措施之一,就是引入Kf值来增大系统中频段的阻尼,但这必然导致减速. 相应地,还需要增加开环放大系数Kc1,以保证系统的响应过程更快速更平稳,称这种设计为结构整定. 整形后系统的结构如图 5所示,它的状态反馈方程如式(16)所示:
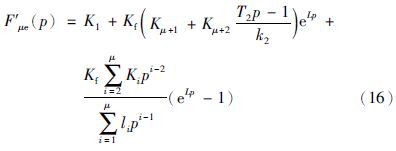
|
| 图 5 二次优化控制控制结构整形 Fig. 5 TOC structure adjustment |
保持式(14)的被控对象的二次优化控制系统控制器参数基本不变,引入Kf和Kc1; 采用人工智能的方法,确定适当的Kf和Kc1值,结果如表 4所示.
| Kf | Kc1 | Kμ+2 | |
| μ=1 | 11 | 20.5 | 3.3 |
| μ=2 | 20 | 32.2 | 9.5 |
| μ=3 | 40 | 49.8 | 16.2 |
当t=13 s时增加-0.2的负荷扰动,系统的阶跃响应曲线如图 6所示,性能指标汇总于表 5.
|
| 图 6 结构整形后系统的响应曲线 Fig. 6 Step response curve after structure adjustment |
| Σ /% | ts | Edm/% | tsd | |
| μ=1 | 0.5 | 4.8 | -0.7 | 0 |
| μ=2 | 0 | 4.2 | -0.3 | 0 |
| μ=3 | 2 | 3.85 | -0.05 | 0 |
比较图 3和图 6、 表 3和表 5可知: 经过结构整形后,控制系统的品质指标得到了全面提高.
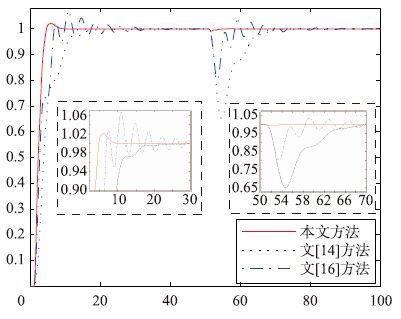
3.2 负载扰动下对比实例仿真以μ=1时结构整形后的系统控制效果为参照,与文[14]和文[16]进行对比: 当t=25 s时突加幅度为-1的负荷扰动,其阶跃响应如图 7所示,相应的性能指标如表 6所示.

|
| 图 6 负载扰动为-100%下的阶跃响应曲线 Fig. 6 Step responses curve when -100% load disturbance occurs |
图 7和表 6指出: 与文[14]、 文[16]相比,μ=1的结构整形后的二次优化控制系统,不仅跟踪响应快速平稳,而且鲁棒性接近无穷大.
3.3 参数扰动下对比实例仿真设K=增加20%,L增加10%,T1和T2减少5%,并当t50 s时,突加幅度为-1的负载扰动,其阶跃响应曲线如图 8所示,相应的性能指标如表 7所示.
|
| 图 8 负载和参数扰动阶跃响应曲线 Fig. 8 Step responses when load and parameter perturbations occur |
图 8和表 7表明: μ=1的二次优化控制系统,其跟踪响应的品质指标σ%×ts虽然与文[14]相近,但抗负荷鲁棒性方面很强; 与文[16]的控制效果相比,则全面皆优. 应该指出: 本文只用了3个分时模型中品质指标最差的μ=1系统与已有方案进行比较,若采用μ=2,3系统进行对比,其控制效果会更好.
4 结束语本文运用二次优化控制原理,设计了一类二阶不稳定时滞系统的优化控制器,基本上消除了被控对象螺旋形的幅相特性,系统跟踪响应快速平稳、 抗扰鲁棒性强; 在此基础上,经结构整形后,系统跟踪响应的快速性、 平稳性和抗扰的鲁棒性又得到大幅度的提高,具有很好的实用价值.
| [1] | 王启志, 王晓霞. 工业过程时滞现象的补偿与控制[J]. 仪器仪表学报, 2011, 31(12): 2836-2841. Wang Q Q, Wang X X. Time-delay compensation and control for industrial process[J]. Chinese Journal of Scientific Instrucment, 2011, 31(12): 2836-2841. |
| [2] | 李明辉, 张洪兴, 刘先保. DMC在苛化工段过灰量控制中的应用与仿真[J]. 计算机仿真, 2014, 31(1): 228-231. Li M H, Zhang H X, Liu X B. Application study and simulation of DMC to line amount control in causticizing department. Computer Simulation[J] , 2014, 31(1): 228-231. |
| [3] | 徐雪松, 欧阳晓. 钢铁炉温不确定时滞系统Smith免疫预测控制[J]. 计算机应用, 2012, 32(10): 2956-2959. Xu X S, Ouyang X. Smith-immune predictive control for steel uncertain time-delay system[J]. Computer Application, 2012, 32(10): 2956-2959. |
| [4] | 唐鑫, 左为恒, 李昌春. 中央空调房间温度智能PID控制的仿真研究[J]. 计算机仿真, 2010, 27(5): 140-144. Tang X, Zuo W H, Li C C. Emulation of intelligent PID control in temperature of central air-conditioning system[J]. Computer Simulation, 2010, 27(5): 140-144. |
| [5] | Seshagiri R A, Chidabaram M. Enhanced two degrees of freedom control strategy for second order unstable processes with time delay[J]. Industrial & Engineering Chemistry Research, 2006, 45(10): 3604-3614. |
| [6] | Matausek M R, Sekara T B. PID controller frequency-domain tuning for stable, integrating and unstable processes, including dead-time[J]. Journal of Process Control, 2011, 21(1): 17-27. |
| [7] | Hu W H, Xiao G X, Li X M. An analytical method for PID controller tuning with specified gain and phase margins for integral plus time delay process[J]. ISA Transcations, 2011, 50(2): 268-276. |
| [8] | Wang Y J. Determination of all feasible robust PID controllers for open-loop unstable plus time delay processes with gain margin and phase margin specifications[J]. ISA Transactions, 2014, 53(2): 628-646. |
| [9] | Pillay N, Govender P. PSO tuned PI/PID controller for open-loop unstable processes with time delay[J]. EPIA'2011, 2011: 223-237. |
| [10] | Pandhan D G, Majhi S. A two degree of freedom control scheme for improved performance of unstable delay process[C]//proceedings of the 2010 International Conferenceon Electricaland Computer Engineering. Piscataway, NJ, USA: IEEE, 2010: 251-254. |
| [11] | Vanavil B, Rao A S. Improved performance with PID filter controllers for unstable processes involving time delays[C]//2011 International Conferenceon Process Automation, Controland Computing. Piscataway, NJ, USA: IEEE, 2011: 1-6. |
| [12] | Vanavil B. Anusha A V N L, Perumalsamy M, et al. Enhanced IMC-PID controller design with lead-lag filter for unstable and integrating processes with time delay[J]. Chemical Engineering Communications, 2014, 201(11): 1468-1496. |
| [13] | Jeng J C, Nasution A, Huang H P. IMC based set-point weighted PID tuning for first order delay unstable process (FODUP)[C]//2011 International Symposiumon Advanced Control of Industrial Processes. Piscataway, NJ, USA: IEEE, 2011: 397-402. |
| [14] | Shamsuzzoha M, Skliar, Lee M. Design of IMC filter for PID control strategy of open-loop unstable processes with time delay[J]. Asia Pacific Journal of Chemical Engineering, 2012, 7(1): 93-110. |
| [15] | Uma S, Rao A S. Enhanced modified Smith predictor for second-order non-minimum phase unstable processes[J]. International Journal of Systems Science, 2014, 47(4): 1-16. |
| [16] | Rao A S, Chidambaram M. Analytical design of modified Smith predictor in a two-degrees-of-freedom control scheme for second order unstable processes with time delay[J]. ISA Transactions, 2008, 47(4): 407-419. |
| [17] | Graham D, Lathrop R C. The synthesis of optimum transient respones: Criteria and standard forms[J]. Transactions of the American Institute of Electrical Engineers, Part Ⅱ: Applications and Industry, 1953, 72(5): 273-288. |
| [18] | 项国波. 时滞系统优化控制[M]. 北京: 中国电力出版社, 2009: 67-111. Xiang G B. Optimal control of time-delay system[M]. Beijing: China Electric Power Press, 2009: 67-111. |
| [19] | 杨益群, 项国波. 单变量时滞系统优化控制[J]. 武汉理工大学学报: 自然科学版, 2007, 29(5): 207-210. Yang Y Q, Xiang G B. Modern optimum control theory for SISO system with delay[J]. Journal of Wuhan University of Technology, 2007, 29(5): 207-210. |
| [20] | Yang Y Q, Xiang G B. Global satisfactory control for nonlinear integrator process with long delay[J]. Journal of Control Theory and Applications, 2007, 5(2): 125-129. |
| [21] | 杨益群, 项国波, 杨启文. 双容纯时滞系统两次优化控制的背驰定律[J]. 信息与控制, 2004, 33(5): 550-553. Yang Y Q, Xiang G B, Yang Q W. A law of run in the opposite direction for the twice optimum control in the system with dead time[J]. Information and Control, 2004, 33(5): 550-553. |
| [22] | 钱业青, 项国波. 纯时滞两次ITAE优化控制系统的背弛定律[J]. 信息与控制, 2000, 29(3): 211-218. Qian Y Q, Xiang G B. A law of run in the opposite direction for the twice ITAE optimum control in the system with dead time[J]. Information and Control, 2000, 29(3): 211-218. |
| [23] | 项国波, 杨益群, 杨启文. 一类单容纯时滞系统二次优化控制[J]. 信息与控制, 1995, 24(4): 209-214. Xiang G B, Yang Y Q, Yang Q W. Twice optimum control for a kind of first order system with dead time[J]. Information and control, 1995, 24(4): 209-214. |
| [24] | 王钦若, 邓九英. 对称极点配置的不稳定时滞系统优化控制[J]. 控制工程, 2012, 19(增刊): 1-4. Wang Q R, Deng J Y. Twice optimal control to unstable system with time-delay using symmetric pole assignment[J]. Control Engineering of China, 2012, 19(sup.): 1-4 |



