2. 长沙高新区创业服务中心,湖南 长沙 410205;
3. 中南大学图书馆,湖南 长沙 410083
2. Changsha High-tech Innovation Service Center, Changsha 410205, China;
3. Central South University Library, Changsha 410083, China
随着人类社会迈入知识经济时代,知识产权产品(专利、 软件、 著作等)在社会中发挥的作用越来越大,成为推动社会经济发展的重要力量. 对国家来说,只有拥有核心知识产权产品才能占领产业链的高端; 对企业来说,知识产权产品已然成为企业尤其是高新技术企业的核心竞争力,是企业发展壮大、 创造利润的重要前提. 在当今科学技术日新月异的时代,企业之间的竞争越来越体现为企业知识产权产品的竞争. 目前,针对知识产权的研究主要是针对其价值评估[1, 2]及战略管理[3, 4],并没有将其与企业决策联系起来.
知识产权产品必须经过大量的实验,耗费巨额研究经费,尤其是在工程机械行业,其开发知识产权产品的花费更大、 耗时更长,而通过购买知识产权产品既可以减少研究经费又可以使生产的产品符合社会需要. 因此,对于一些刚起步的工程机械企业,其资金、 人力有限,通过购买高新知识产权产品来生产其需要的产品更为可取. 然而,在这个知识经济时代,充斥着许多知识产权产品,其性能、 价格、 侧重点都各不相同,而企业由于刚进入这个行业,对行业了解不深,从而不能很准确地选择符合其需求的知识产权产品. 因此,本文针对工程机械企业对知识产权产品选择困难的问题,利用群决策方法根据工程机械企业自身的情况与需求为其推荐合适的知识产权产品.
群决策就是依据一定的规则把不同领域专家的偏好集结为决策群体偏好,并对其进行分析[5]. 首先将专家构成一个决策群体,并通过其对工程机械企业需求的了解,对可选的知识产权产品进行判断、 评价. 由于知识产权产品的复杂性与决策专家个人因素等原因,决策专家往往无法对知识产权产品直接给出效用值,而根据自己对工程机械企业需求的了解,对两两知识产权产品进行比较给出偏好关系更为容易. 偏好关系可分为3类: 模糊偏好关系、 乘性偏好关系与语言偏好关系,其中模糊偏好关系由于其应用的简便性而受到广泛应用. 因此本文采用模糊偏好关系来表示决策专家对知识产权产品的决策偏好信息,在此基础上利用群决策方法进行知识产权产品推荐.
由于工程机械企业购买一项知识产权产品对企业的经营与发展有着重大影响,企业必须谨慎地选择知识产权产品. 因此,所推荐的产品必须尽可能得到决策专家的认同,而群决策涉及多个决策专家,其对工程机械企业需求与知识产权产品的了解程度、 所考虑的侧重点各不相同,对知识产权产品的偏好也不同,从而使得专家对知识产权产品的最终推荐结果不能达成共识,从而降低推荐结果的可信度. 因此,必须对专家之间的共识进行测度与控制,通过一定的方法增加决策专家之间的共识程度[6, 7, 8]. 同时决策专家所给出的模糊偏好关系的一致性影响到专家对产品的客观评价,从而影响企业对专家推荐结果的信任. 因此,在对共识进行测度的同时必须对专家偏好的一致性进行测度与控制[9, 10]. 目前,同时对一致性与共识进行测度与控制的研究较少且都是在对共识控制之前首先对一致性进行控制,而没有对其同时进行控制[11, 12]. 因此,本文在知识产权产品推荐群决策过程中同时考虑专家的一致性与共识程度,并对其同时进行控制.
当专家偏好一致性与共识程度达到一定程度时,便可对产品进行排序选优,目前群决策排序方法主要是针对效用值,少有针对偏好关系: Perez[13]与Wu[14]分别利用量词引导优势度与非优势度方法对方案进行排序. 因此,本文同时结合量词引导优势度与非优势度方法对知识产权产品进行排序选优. 综上所述,本文为工程机械企业提出一种知识产权产品推荐群决策方法,在决策过程中对专家的一致性与共识同时进行控制,并结合量词引导优势度与非优势度方法对其进行选优.
2 工程机械知识产权产品推荐群决策框架工程机械知识产权产品推荐群决策主要包括两个过程: 一致性/共识控制过程与产品推荐过程. 本文方法有以下两个特点: 一是该方法在产品推荐之前对决策专家偏好的一致性与共识进行控制,通过反馈机制对一致性/共识水平过低的决策专家偏好进行修正,增加推荐结果的可信度; 二是在产品推荐过程中,同时采用量词引导优势度与非优势度方法对产品进行排序选优. 工程机械知识产权产品推荐群决策框架如图 1所示.

|
| 图 1 工程机械知识产权产品推荐群决策框架 Fig. 1 The group decision making framework of construction machinery intellectual property product recommendation |
首先决策专家E={e1,e2,…,em}(m≥2)针对可供选择的知识产权产品集X={x1,x2,…,xn}(n≥2)给出其相应的模糊偏好关系Pk=(pijk)(k=1,2,…,m). 其中pijk表示决策专家ek对产品xi与产品xj的偏好程度: pijk=0.5表示决策专家ek认为产品xi与产品xj同等重要(xi~xj),pijk>0.5说明决策专家ek认为产品xi优于产品xj(xi$\prec $xj); pijk<0.5则说明决策专家ek认为产品xj优于产品xi(xi$\prec $xj),同时模糊偏好关系满足pijk+pjik=1,∀i,j∈{1,2,…,n}. 然后对每位决策专家偏好关系的一致性与共识指数进行测度,结合这两个指标得到每位决策专家的一致性/共识指数(L),并将其与决策之前所确定的阈值λ进行比较. 当所有决策专家的一致性/共识指数大于等于阈值λ时,可以直接进入产品推荐过程对产品进行排序选优,将最适合的知识产权产品推荐给工程机械企业; 否则需进入反馈机制对偏好进行识别与修正,提高其一致性/共识指数.
阈值λ的大小与所处理的决策问题有关[15, 16]: 当最终的选择结果对问题的影响非常大时,阈值需尽量大; 而当决策结果对问题影响不是很大,同时决策时间紧迫的情况下,阈值可设得小一些.
3 决策偏好一致性/共识控制过程一致性/共识控制过程是一个循环迭代的过程,目标是得到高一致性与高共识的产品推荐结果,主要包括4个部分: 决策偏好一致性测度、 决策偏好共识测度、 一致性/共识水平判断、 反馈机制.
3.1 决策偏好一致性测度偏好一致性可分为3个层次: 两两产品层、 产品层与偏好关系层,可通过加性传递性[17]来测度,如式(1)所示:

通过式(1)能够利用偏好关系中其余偏好值来计算得到某一个偏好值的估计值qil:
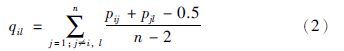
Level 1: 两两产品层的偏好一致性指数Cil:

Level 2: 产品层的偏好一致性指数Ci:

Level 3: 偏好关系层的偏好一致性指数C:

偏好共识也可分为两两产品层、 产品层与偏好关系层三个层次,首先计算任意两两决策专家之间的相似度,然后再分别对3个不同层次的共识进行计算得到某个决策专家的偏好共识程度. 其具体步骤如下:
Step 1: 对任意两个决策专家(ek,eh),得到一个相似矩阵Skh=(sijkh),其中:

Step 2: 计算决策专家ek的偏好共识指数,分别从3个不同层次来计算:
Level 1: 两两产品层的偏好共识指数:

Level 2: 产品层的偏好共识指数:

Level 3: 偏好关系层的偏好共识指数:

一致性/共识水平判断过程是用来判断是否可以结束一致性/共识控制过程进入产品推荐过程. 由于同时考虑了偏好一致性与共识指数,需定义一个一致性/共识水平(L):

当所有决策专家的一致性/共识水平大于或等于阈值λ时,就结束一致性/共识控制过程. 由于决策具有时间限制,需设定一个最大循环次数T来限制一致性/共识控制过程的次数. 如果有决策专家的一致性/共识指数小于阈值,将一致性/共识控制次数t与最大循环次数T进行比较: 当t<T时,可进入反馈机制对偏好进行修正; 否则,结束一致性/共识控制过程,进入产品推荐过程.
3.4 反馈机制当存在决策专家的一致性/共识指数小于阈值且一致性/共识控制次数t没有达到最大循环次数T时,需进入反馈机制对偏好进行识别与修正. 反馈机制分为2个阶段: 识别阶段与建议阶段[6].
(1) 识别阶段. 识别阶段可根据一致性与共识指数的3个层次分为3个步骤,即识别出需要修正偏好的决策专家、 识别出需修正偏好所对应的产品集及识别出需要修正的偏好值.
Step 1: 识别决策专家. 找出需要接受建议修正其偏好信息的决策专家E,其偏好关系层的一致性/共识指数小于阈值λ:

Step 2: 识别产品. 找出上述决策专家需修正的偏好所对应的产品集,其产品层的一致性/共识指数小于阈值λ,用A表示:

Step 3: 识别偏好. 找出上述决策专家需要修正的偏好值,其两两产品层的一致性/共识指数小于阈值,用H表示:

(2) 建议阶段. 识别出决策专家需要修正的偏好之后,就需要对其提供修正建议. 本文在对专家偏好进行修正时同样考虑了专家的偏好一致性与共识两个指标,同时考虑了决策专家修正偏好的主观意愿,利用式(11)来对偏好进行修正:

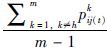 . δ的含义见式(10); μt表示第t次一致性/共识控制过程中决策专家eh的偏好修正系数,表示决策专家eh愿意修正其偏好的程度.
4 知识产权产品推荐过程
. δ的含义见式(10); μt表示第t次一致性/共识控制过程中决策专家eh的偏好修正系数,表示决策专家eh愿意修正其偏好的程度.
4 知识产权产品推荐过程当所有决策专家的一致性/共识水平达到阈值水平或一致性/共识控制次数t达到最大循环次数T时,就可以进入产品推荐过程对知识产权产品进行排序选优. 知识产权产品推荐过程包括2个阶段: 个体偏好集结与群体偏好分析[13, 14].
4.1 个体偏好集结个体偏好集结是指通过一定的方式将所有决策专家的偏好结合得到群体偏好. 首先需要得到每位决策专家的权重,可通过每位决策专家的一致性/共识指数来计算[18, 19],如式(12)所示:


本文结合量词引导优势度(quantifier guided dominance degree,QGDD)与量词引导非优势度(quantifier guided non-dominance degree,QGNDD)方法对群体偏好进行分析从而得到知识产权产品的推荐结果. 这个方法的基础是有序加权平均算子(ordered weighted averaging,OWA). OWA算子的特点是对选择对象(a1,a2,…,an)按从大到小的顺序重新进行排序并通过加权将其集结[20],如式(14)所示:


量词引导优势度(QGDD)方法是指测量某个产品xi优于其它产品的程度:

量词引导非优势度(QGNDD)方法是指测量某个产品xi没有被其它产品超越的程度:
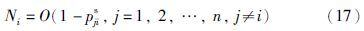

最后可通过式(18)来得到最终推荐产品,是最大程度优于其余产品同时最大程度没有被其余产品超越的产品:
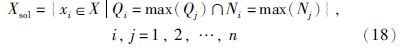
现以向某工程机械企业推荐一种起重机专利为例来验证该群决策方法的实现过程及其有效性. 首先,从众多专利中筛选出4种适合其企业情况与生产需求的专利,分别是: (1)轮胎式集装箱门式起重机; (2)双向行走索道起重机; (3)单臂架钢丝绳变幅固定式起重机; (4)洁净无尘起重机. 然后聘请5位工程机械起重机机方面的专家E={e1,e2,e3,e4,e5},针对该工程机械企业的情况与将要生产的起重机的需求,对上述4种专利X={x1,x2,x3,x4}进行分析评价,给出其相应的模糊偏好关系,然后利用本文方法对专利进行排序选优,得到最满足企业需求与专家认可度高的推荐结果. 在决策之前,首先由所有决策专家根据企业的具体情况与时间限制确定阈值λ=0.80,最大循环次数T=8,共识所占的重要性程度σ=0.8,群决策步骤如5.1节和5.2节所示.
5.1 偏好一致性/共识控制过程(1) 第1阶段
Step 1: 5位决策专家通过对企业需求与各专利的了解分别给出其模糊偏好关系:

Step 2: 利用式(1)~(5)计算得到每位决策专家的偏好一致性指数:
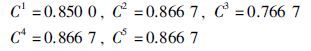
Step 3: 利用式(6)~(9)计算每位决策专家的偏好共识指数:

Step 4: 利用式(10)计算每位决策专家的一致性/共识指数:
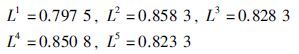
(2) 第2阶段
Step 1: 通过反馈机制识别出需要修正偏好的决策专家E={h1}及需要修正的偏好值为H={(1,4,1),(1,4,2),(1,4,3)},此时决策专家e1给出其偏好修正系数μ=0.8,利用式(11)对偏好进行修正,得到新的偏好关系:

Step 2: 重新计算决策专家e1的偏好一致性指数C1=0.885 0.
Step 3: 计算每位决策专家的偏好共识指数:

Step 4: 计算每位决策专家的一致性/共识指数:
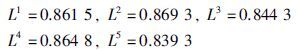
此时所有决策专家的一致性/共识指数都大于阈值λ,可以结束一致性/共识控制过程,进入产品推荐过程.
5.2 产品推荐过程Step 1: 利用式(12)计算每位决策专家的权重为ωk=[0.201 3,0.203 2,0.197 3,0.202 1,0.196 1],并利用式(13)得到群体偏好:
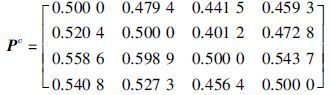
Step 2: 通过式(15)计算得到位置权重: Wj=[0.577 4,0.239 1,0.183 5],并利用式(16)、 (17)计算各方案的量词引导优势度指数: Q=[0.467 6,0.487 3,0.579 1,0.522 1]与量词引导非优势度指数: N=[0.935 3,0.930 7,1.00 0,0.984 0],然后利用式(18)得到最优专利产品为x3,决策过程结束.
5.3 结果分析以上结果是利用本文方法所得到的,为了说明该方法的有效性,下面采用没有对决策专家的偏好一致性与共识进行控制的传统群决策方法对算例进行分析,即在第1阶段后直接进入产品推荐过程.
首先利用决策专家的偏好一致性/共识指数得到其权重ωk=[0.191 8,0.206 4,0.199 2,0.204 6,0.198 0],并得到群体偏好:

然后对群体偏好进行分析可得到各方案的量词引导优势度指数: Q=[0.482 3,0.494 6,0.593 0,0.483 3]与量词引导非优势度指数: N=[0.964 6,0.962 2,1.000 0,0.963 8]. 最后对两种方法的最终推荐结果进行比较,如表 1所示.
| 方法 | QGDD | QGNDD |
| 基于一致性与共识的群决策方法 | x3$\succ $x4$\succ $x2$\succ $x1 | x3$\succ $x4$\succ $x1$\succ $x2 |
| 传统群决策方法 | x3$\succ $x2$\succ $x4$\succ $x1 | x3$\succ $x1$\succ $x4$\succ $x2 |
从表 1可观察到,两种不同的方法得到的产品排序结果是不同的,但是最优的产品是一致的,都是产品x3,因此本文所采用的方法是有效的. 同时,在推荐结果一致的情况下,基于一致性与共识的群决策方法使决策专家的偏好一致性与共识都达到了较高的水平,增加了工程机械知识产权产品推荐结果的可信度,使工程机械企业更容易接受推荐结果.
6 结论本文针对工程机械企业对知识产权产品选择困难的问题,提出一个为企业推荐知识产权产品的群决策方法. 该方法在决策过程中对专家的一致性与共识同时进行控制,通过考虑决策专家的偏好一致性来保证决策专家所给出的评价信息的合理性; 考虑决策专家的偏好共识来保证决策群体对最终产品的认同. 这样得到的推荐结果不仅满足最优条件,而且在很大程度上得到所有决策专家的认同,从而使企业更容易接受推荐结果. 当所有决策专家的一致性/共识指数都达到阈值水平时,结合量词引导优势度与非优势度方法对产品进行排序选优,得到最优推荐结果. 由于工程机械行业专家专业知识有限,在对产品进行评价时偏好的不确定性大,使得模糊偏好关系不能满足其表述,因此后续研究需要考虑采用区间模糊偏好关系或语言偏好关系来表示决策专家的偏好.
| [1] | 姜秋, 王宁. 基于模糊综合评价的知识产权价值评估[J]. 技术与创新管理, 2005(6): 73-76. Jiang Q, Wang N. Intellectual property appraisal by fuzzy multiple goals decision-making method[J]. Technology and Innovation Management, 2005(6): 73-76. |
| [2] | 王竞达. 跨国并购知识产权价值评估相关问题研究[J]. 经济与管理研究, 2010(5): 69-77. Wang J D. Research on value assessment issues of intellectual property in international merger[J]. Research on Economics and Management, 2010(5): 69-77. |
| [3] | 姜甫, 胡允银. 企业知识产权战略成本管理研究[J]. 科技管理研究, 2012(3): 139-143. Jiang F, Hu Y Y. Study on the strategic cost management of intellectual property in enterprise[J]. Science and Technology Management Research, 2012(3): 139-143. |
| [4] | 孙伟, 姜彦福. 企业知识产权战略架构及其选择模型: 基于战略管理的视角[J]. 科学学与科学技术管理, 2009, (02): 23-28. Sun W, Jiang Y F. Enterprise intellectual property rights structure and its strategic choice model: Based on the perspective of strategic management[J]. Science of Science and Management of S. & T., 2009(2): 23-28. |
| [5] | Hwang C, Lin M. Group decision making under multiple criteria[M]. Berlin, Germany: Springer, 1987. |
| [6] | Perez I J, Cabrerizo F J, Alonso S, et al. A new consensus model for group decision making problems with non-homogeneous experts[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2014, 44(4): 494-498. |
| [7] | Zhang L, Li T, Xu X. Consensus model for multiple criteria group decision making under intuitionistic fuzzy environment[J]. Knowledge-Based Systems, 2014, 57: 127-135. |
| [8] | Parreiras R O, Ekel P Y, Martini J S C, et al. A flexible consensus scheme for multicriteria group decision making under linguistic assessments[J]. Information Sciences, 2010, 180(7): 1075-1089. |
| [9] | Chiclana F, Herrera-Viedma E, Alonso S, et al. Cardinal consistency of reciprocal preference relations: A characterization of multiplicative transitivity[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(1): 14-23. |
| [10] | Liu X, Pan Y, Xu Y, et al. Least square completion and inconsistency repair methods for additively consistent fuzzy preference relations[J]. Fuzzy Sets and Systems, 2012, 198: 1-19. |
| [11] | Chiclana F, Mata F, Martinez L, et al. Integration of a consistency control module within a consensus model[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2008, 16(sup.1): 35-53. |
| [12] | Wu Z, Xu J. A consistency and consensus based decision support model for group decision making with multiplicative preference relations[J]. Decision Support Systems, 2012, 52(3): 757-767. |
| [13] | Perez I J, Cabrerizo F J, Herrera-Viedma E. A mobile decision support system for dynamic group decision-making problems[J]. IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 2010, 40(6): 1244-1256. |
| [14] | Wu J, Chiclana F. A social network analysis trust-consensus based approach to group decision-making problems with interval-valued fuzzy reciprocal preference relations[J]. Knowledge-Based Systems, 2014, 59: 97-107. |
| [15] | Mata F, Martinez L, Herrera-Viedma E. An adaptive consensus support model for group decision-making problems in a multigranular fuzzy linguistic context[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(2): 279-290. |
| [16] | Xu J, Wu Z, Zhang Y. A consensus based method for multi-criteria group decision making under uncertain linguistic setting[J]. Group Decision and Negotiation, 2014, 23(1): 127-148. |
| [17] | Tanino T. Fuzzy preference orderings in group decision making[J]. Fuzzy sets and systems, 1984, 12(2): 117-131. |
| [18] | Chiclana F, Herrera-Viedma E, Herrera F, et al. Some induced ordered weighted averaging operators and their use for solving group decision-making problems based on fuzzy preference relations[J]. European Journal of Operational Research, 2007, 182(1): 383-399. |
| [19] | Wu J, Cao Q, Zhang J. Some properties of the induced continuous ordered weighted geometric operators in group decision making[J]. Computers & Industrial Engineering, 2010, 59(1): 100-106. |
| [20] | Fodor J, Marichal J L, Roubens M. Characterization of the ordered weighted averaging operators[J]. IEEE Transactions on Fuzzy Systems, 1995, 3(2): 236-240. |
| [21] | Yager R R. Quantifier guided aggregation using owa operators[J]. International Journal of Intelligent Systems, 1996, 11(1): 49-73. |



