2. 辽河油田分公司锦州采油厂采油作业五区,辽宁 锦州 121209
2. The Fifth District of Jinzhou Oil Production Plant, Liaohe Oilfield Company, Jinzhou 121209, China
混沌系统在社会生活中普遍存在,混沌时间序列的预测越来越受到人们的重视,已在很多领域得到应用,例如天气情况[1]、 交通运输[2]、 金融市场[3]、 网络流量预测[4]等方面. 混沌时间序列预测中所涉及的非线性问题在很大程度上决定了预测的精度,而传统的自回归(auto regression,AR)[5]、 自回归综合移动平均(auto regressive integrated moving average,ARIMA)[6]等线性模型已经不能很好地处理这个问题. 目前,很多基于非线性模型的方法已经应用于混沌时间序列的预测中,如人工神经网络[7]、 支持向量机(support vector machine,SVM)[8]、 灰色模型[9]、 模糊模型[10]等.
最小二乘支持向量机(least square support vector machine,LSSVM)是SVM的改进,由Suykens等人提出[11],将SVM中所存在的训练需要求解二次规划的问题转化为求解线性方程组的问题,以提高学习速度. 将LSSVM应用于混沌时间序列的预测是目前该领域研究的一个热点,其中涉及两个较为重要的问题,一个是LSSVM建模中参数的优化问题,另一个是算法在实现过程中存在的过拟合问题. 为了确定最优的参数,文[12]采用改进的遗传算法进行LSSVM模型的参数的优化选择,交叉和变异以自适应的方式进行操作,较之传统的遗传算法有更好的收敛效果; 文[13]采用粒子群算法进行LSSVM模型的参数的优化选择; 文[14]提出了蚁群非均匀嵌入维数算法,采用蚁群算法对时间序列的嵌入维数和延迟时间参数进行优化选择,将选择过程划分为两个阶段,具有较好的优化性能和预测精度; 文[15]给出精细指数加权模糊时间序列,采用改进的和声搜索算法对区间长度等参数进行优化选择,从而减小预测误差,所提出的改进和声搜索算法采用新的和声向量表示方法,具有较好的搜索效果. 但是,这些优化方法存在相关参数的准确设定问题,一般依赖于人工经验给定,因此LSSVM模型的预测精度受其影响较大. 例如: 遗传算法中的编码串长、 交叉概率和变异概率等,粒子群算法中的惯性权重和学习因子等,模拟退火算法中的退火温度、 退火方式和退火系数等,蚁群算法中的信息素重要程度因子、 启发式因子重要程度系数、 转移概率判断因子、 信息素蒸发系数和信息素增加强度系数等,和声搜索算法中的和声记忆库的和声数、 和声记忆库保留概率、 记忆扰动概率和带宽范围等.
过拟合可以理解为模型在训练中过分追求对训练样本的拟合精度,而导致对其它预测样本效果变差的现象. 特别是在一些实际工业过程应用中,由于训练样本中可能会存在噪声或者工况变化的情况,过拟合的问题需要重视. 为了有效地解决这个问题,文[16]采用快速留一交叉验证法(fast leave-one-out cross-validation,FLOO-CV)进行模型参数的自适应选取,取得了较好的预测效果.
本文采用LSSVM进行混沌时间序列的预测,核函数采用径向基核函数. 针对参数优化选取中所存在的主要问题,采用一种改进的黑洞(improved black hole,IBH)算法选择最优参数,整个算法过程不需要额外设定任何主观参数,避免了过多参数设定对预测精度的影响,算法实现过程中当一个候选解被“吸收”后,会在解空间中随机生成一个新的候选解,保证了可行解数量的稳定,算法结构简单、 易于实现; 对于算法可能存在的过拟合情况,采用基于FLOO的方法估计泛化误差,进行在线校验,判断得到的最优参数是否合理. 将其应用于抽油井动液面的短期预测中,可以提高油田生产的安全性和合理性.
2 基于LSSVM的混沌时间序列预测 2.1 LSSVM给定训练集{(x1,y1),(x2,y2),…,(xi,yi)},i=1,2,…,l. xi∈Rm为m维输入样本矢量,yi∈R为1维输出样本矢量.
采用如下函数进行预测:

根据文[11],建立拉格朗日等式,构造无约束优化问题,采用最小二乘法进行求解,得到的输出可以表示为

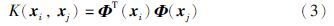
本文采用径向基核函数,定义如下:

设混沌时间序列为{xi,i=1,2,…N},通过相空间重构得到如下序列形式: Xt=[xt,xt+τ,…,xt+(m-1)τ],t=1,2,…,M,其中m为嵌入维数,τ为延迟时间,M=N-(m-1)τ. 有研究认为选择合理的m和τ可以使重构的相空间在一定程度上与原系统有相同的拓扑性质. 时间序列的预测输出可以表示为Yt=xt+1+(m-1)τ,t=1,2,…,M,将Xt和Yt分别作为LSSVM的输入和输出即可完成建模. 本文采用单步预测,即每预测出一个Yt后,将其加入到下一个输入Xt+1的最后一维中.
在基于LSSVM的混沌时间序列预测中,嵌入维数m和延迟时间τ决定了所重构的相空间是否逼近于原空间,正则化参数γ和核函数参数σ2决定了LSSVM的性能. 因此,上述4个参数,m、 τ、 γ和σ2决定了LSSVM预测模型的预测精度. 本文采用IBH算法进行这4个参数的寻优,以提高预测模型的精度.
3 改进的黑洞(IBH)算法 3.1 黑洞(BH)算法黑洞(black hole,BH)算法是Hatamlou[17]于2013年提出的一种新的启发式优化算法,其主要步骤如下:
步骤1 初始化阶段,将解空间中的所有候选解定位为“星星”.
步骤2 计算每个“星星”的适应度函数值,将具有最优适应度函数值的“星星”看作“黑洞”.
步骤3 “星星”向“黑洞”移动,位置的变化可以由如下公式进行描述:

步骤4 如果改变位置后的“星星”的适应度函数值比“黑洞”更优,那么就互换它们的位置.
步骤5 若“星星”移动到“黑洞”的范围内,那么“星星”会被“黑洞”吸收,“黑洞”的半径由如下公式描述:

当某个“星星”和“黑洞”的距离小于RBH时,这个“星星”会被“黑洞”吸收而消失,同时在搜索空间内会随机生成一个新的“星星”.
步骤6 如果满足终止条件,停止迭代; 否则返回步骤3重新迭代.
BH算法具有整个搜索过程不需要额外设定任何主观参数、 易于实现等优点. 但是,也应该看到,由于“星星”被“黑洞”吸收后会随机生成一个新的“星星”的搜索机制,BH算法的运算时间较长. 因此,为了提高搜索的收敛效果,本文提出改进的BH算法(IBH).
3.2 改进的黑洞(IBH)算法相比于BH算法,本文所提出的IBH算法在位置更新机制、 吸收机制、 适应度函数的计算和防止过拟合等几个方面作了相应的改进.
3.2.1 “星星”位置的更新机制“星星”位置的更新机制决定了优化算法能否找到全局最优解,如果条件太严格,很容易使算法陷入局部最优; 如果条件过于宽松,会降低算法的收敛能力. 由式(5)可以看到,每个“星星”的位置移动受到当前一个最优个体——“黑洞”的指引,搜索方向是否正确完全由其信息所决定,极易陷入局部最优. 对此,本文对“星星”位置的更新机制作了如下改进,即:
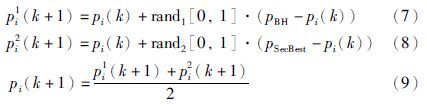
根据BH算法的步骤5,当某个“星星”和“黑洞”的距离小于“黑洞”的半径时,这个“星星”会被“黑洞”吸收,同时随机生成一个新的“星星”. 这种机制使搜索空间中候选解数量恒定,且保证能在整个空间中搜索全局最优解. 但是,这样一种机制决定了会耗费较多的运算时间,因为吸收“星星”并产生新的“星星”使搜索过程在一定程度上会产生坏解,降低了算法的收敛速度. “星星”被“黑洞”吸收的关键在于“黑洞”半径的计算,如果半径过小,“星星”的更新较少,易陷入局部最优; 如果半径过大,被“黑洞”吸收的“星星”过多,会增长搜索的时间,算法收敛较慢.
式(6)定义了BH算法中“黑洞”的半径,即“黑洞”的适应度函数值与所有“星星”适应度函数值之和的比值. 但是,这种半径的定义使算法在搜索时极易陷入早熟收敛的情况,因为过于追求搜索局部最优. 为了增加算法的全局搜索能力,本文所提出的IBH算法对“黑洞”半径进行了重新定义:

当rand[0,1]=0时,有:
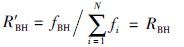
当rand[0,1]=1时,有:

当rand[0,1]在[0,1]内取值时,算法既有局部搜索能力,又有全局搜索能力.
在BH算法中,当一个“星星”被“黑洞”吸收后,会在解空间内随机生成一个新的“星星”,这种生成新解的机制完全是随机的,并没有考虑已有解的信息,虽然在一定意义上具有跳出局部最优的能力,但是完全是以牺牲收敛速度为代价,会造成整个算法运算时间过长、 收敛性差. 对此,本文的IBH算法对新的“星星”的产生机制进行了改进,定义如下:

BH算法中,当“星星”被“黑洞”吸收后同时会产生新的“星星”,进入下一次迭代,然后计算所有“星星”的适应度函数值,将具有最优适应度函数值的“星星”作为“黑洞”. 但是,在每一次迭代中,并不是所有“星星”的位置都一定发生变化,即它们的适应度函数值并没有变化. 这由式(7)~式(9)可以看出,当rand1[0,1]和rand2[0,1]都为0时,有:

如果在下一次的迭代中仍然计算所有“星星”的适应度函数值,就存在重复计算导致浪费运算时间的问题. 因此,在IBH算法中,当进行下一次迭代时,只计算新产生以及位置更新的“星星”的适应度函数值,而对于其它的“星星”则不再计算它们的适应度函数值,这样可以大大提高算法的收敛速度.
3.2.4 基于FLOO方法的在线校验为了便于描述,将数据集中的每一个输入输出数据对称作节点. 借鉴文[16]的方法,将IBH算法第k次迭代得到的参数代入模型,当排除第1个节点时,得到模型对第1个节点的估计值为$\hat{y}_{1}^{\left( -k \right)}$,基于FLOO方法对第1个节点的预报误差为



采用基于FLOO的方法对寻优参数进行在线校验. 算法每一次迭代都会得到当前最优解,采用FLOO方法计算每一次迭代中当前最优解的全样本预报总误差; 当算法结束时,判断全局最优解所对应的预报总误差是否最小,若为最小值,则输出得到的全局最优解,否则重新计算.
3.2.5 IBH算法IBH算法的主要步骤如下:
步骤1 初始化,将解空间中的所有候选解定位为“星星”.
步骤2 计算每个“星星”的适应度函数值,将具有最优适应度函数值的“星星”看作“黑洞”. 将“黑洞”所代表的当前最优参数代入模型,采用基于FLOO方法计算初始状态下全样本的预报总误差.
步骤3 “星星”向“黑洞”移动,位置的变化由式(7)~式(9)描述. 其中,“黑洞”的半径R′BH由式(10)描述.
步骤4 计算新产生以及位置改变的“星星”的适应度函数值,如果比“黑洞”更优,那么就互换它们的位置. 如果“黑洞”发生变化,将其所代表的当前最优参数代入模型,采用基于FLOO的方法计算全样本的预报总误差.
步骤5 如果“黑洞”和“星星”之间的距离d<R′BH,那么这个“星星”会被“黑洞”吸收而消失,同时在搜索空间内会根据式(11)生成一个新的“星星”.
步骤6 如果满足终止条件,停止迭代,将当前最优解记为全局最优解,进行基于FLOO方法的在线校验. 若其全样本预报总误差为最小值,则输出当前参数; 否则返回步骤3重新迭代.
步骤7 更新数据序列. 当产生一个预测值,将其作为新的序列值加入数据序列,同时删除基于FLOO方法所计算的预报误差最小的序列值[18],重复以上步骤.
4 IBH-LSSVMIBH-LSSVM预测模型的计算过程如下:
步骤1 设定待优化参数m、 τ、 γ和σ2的取值范围,其中,m∈[1,60],τ∈[1,10],γ∈[0.01,1 000],σ2∈[0.01,1 000].
步骤2 归一化待处理的混沌时间序列样本数据,归一化区间为[0,1],确定其输入和输出,并按照LSSVM预测算法进行训练和建模. 归一化公式如下:

步骤3 采用IBH算法进行参数的优化选取,将混沌时间序列的实际值和预测值的均方根误差作为适应度函数,定义如下:

终止条件为满足最大迭代次数或得到一个足够好的适应度函数值(5代内不发生变化).
步骤4 如果满足终止条件,将当前解记为最优解,输出记录的最优参数; 如果不满足终止条件,返回步骤3重新迭代.
步骤5 将得到的最优参数进行混沌时间序列的预测,对得到的预测结果进行反归一化处理.
5 仿真实验分析为了说明IBH算法比BH算法在收敛速度和收敛精度上具有更好的效果,下面采用Henon映射混沌序列进行仿真分析.
Henon映射为一个二维映射,是高维映射中最简单的非线性映射,常用于数字图像的加密处理中. 由如下数学公式描述:

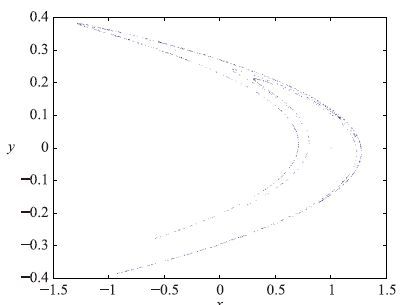
当a=1.4和b=0.3时,系统进入混沌状态. 图 1为Henon映射的混沌吸引子,包含1 000组数据. 图 2为产生的1 000组Henon映射混沌序列中的x(t)和y(t).
|
| 图 1 映射的混沌吸引子 Fig. 1 Chaotic attractors of the Henon mapping |

|
| 图 2 Henon映射混沌序列中的x(t)和y(t) Fig. 2 x(t) and y(t) of the Henon mapping chaotic series |
选取501~700的200组数据作为训练样本用以建立预测模型,701~800的100组数据作为测试样本,设定进化代数为100代. 设定x维预测LSSVM的参数γ=812.9和σ2=2.62,y维预测LSSVM的参数γ=668.4和σ2=0.94,混沌时间序列的参数都为m=4和τ=1,分别采用IBH-LSSVM和BH-LSSVM预测模型进行预测. 图 3为IBH算法和BH算法的适应度变化曲线,可以看到在相同的LSSVM参数下,IBH算法具有更好的收敛效果.

|
| 图 3 适应度曲线 Fig. 3 The fitness curve |
抽油井是国内外油田的主要采油方式,其工作原理是将抽油泵沉没于动液面下,依靠往复举升运动将原油输送到地面. 动液面是抽油井生产的一个重要参数,能够反映抽油井的工作效率. 抽油泵相对于动液面过高会造成空抽甚至烧泵的情况; 相对于动液面过低会造成抽油泵负载增加,产量降低,耗能严重. 在抽油井的连续生产中,动液面会由于生产条件的变化而不断变化,因此,若能准确掌握动液面的变化情况,对于掌握抽油井的供液能力,确定抽油泵的沉没度和冲次,从而制定合理的工作制度以提高生产效率具有十分重要的意义.
根据油田实际生产情况,本文所研究的抽油井动液面短期预测主要预测未来几周的动液面变化情况. 采集国内某油田一口抽油井在一段生产周期内的310组动液面数据,如图 4所示.

|
| 图 4 动液面数据 Fig. 4 The dynamic fluid level data |
要实现抽油井动液面的短期预测,首先需要对数据序列的混沌特性进行分析,如果证明动液面序列具有混沌特性,就可以采用所提出的IBH-LSSVM预测模型进行预测. 具体步骤如下:
步骤1 进行抽油井动液面序列的相空间重构,选取合适的延迟时间τ和嵌入维数m.
步骤2 计算重构后相空间的李亚普诺夫指数,若最大李亚普诺夫指数大于0,则说明该序列一定是混沌的.
步骤3 建立IBH-LSSVM预测模型,进行预测.
下面根据以上步骤进行抽油井动液面的短期预测.
(1) 延迟时间τ和嵌入维数m的计算.
计算延迟时间τ比较复杂,方法也比较多,如自相关法、 平均位移法、 复自相关法、 互信息法等; 计算嵌入维数m的方法有假近邻法、 Cao法等. 本文采用同时求延迟时间与嵌入窗的C-C法[19]计算τ和m,C-C法采用统计结果,计算量小、 容易实现且抗噪能力强. C-C法认为τ和m具有相关性,可以由最佳延迟时间τbest和所对应的最佳嵌入窗τwin,根据式(21)推导出嵌入维数m.

由C-C法可以得到能够反映时延序列自相关特性的曲线:$\bar{S}$ (t)、 Δ$\bar{S}$(t)和Scor(t).
由图 5中的Δ$\bar{S}$(t),第1个局部极小值点为τ=1,即τbest=1; 由Scor(t),全局最小值点为τ=25,即τwin=25. 根据式(21),嵌入维数m=26.

|
| 图 5 $\bar{S}$(t)、 Δ$\bar{S}$(t)和Scor(t) Fig. 5 $\bar{S}$(t),Δ$\bar{S}$(t) and Scor(t) |
(2) 最大李亚普诺夫指数的计算.
由小数据量法[20]求取最大李亚普诺夫指数,代入延迟时间τ=1和嵌入维数m=26,设置最大延迟时间为τmax=100,得到的最大李亚普诺夫指数λ1=0.121 5. 因为λ1>0,因此抽油井动液面序列可看作一个混沌时间序列,在一定范围内具有可预测性,通过预测模型进行动液面的预测是完全可行的.
选取前260组数据作为训练样本用以建立预测模型,后50组数据作为测试样本,设定进化代数为100代. 将本文所提出的预测模型与PSO-LSSVM[13]预测模型、 GA-LSSVM[12]预测模型、 SA-LSSVM[21]预测模型、 AC-LSSVM[14]预测模型和HS-LSSVM[15]预测模型进行比较.
PSO-LSSVM中的相关参数设置如下: 惯性权重ω=1,学习因子c1=1.5和c2=1.7; GA-LSSVM中的相关参数设置如下: 编码串长为10,交叉概率pc=0.6,变异概率pm=0.001; SA-LSSVM中的相关参数设置如下: 退火温度t0=90℃,退火方式为t′=at,退火系数a=0.9; AC-LSSVM的相关参数设置如下: 信息素重要程度因子α=1,启发式因子重要程度系数β=5,转移概率判断因子P0=0.2,信息素蒸发系数P=0.8,信息素增加强度系数Q=0.2; HS-LSSVM中的相关参数设置如下: 和声记忆库的和声数M=30、 和声记忆库保留概率HMCR=0.9,记忆扰动概率PAR=0.1,带宽范围为[0.001,1].
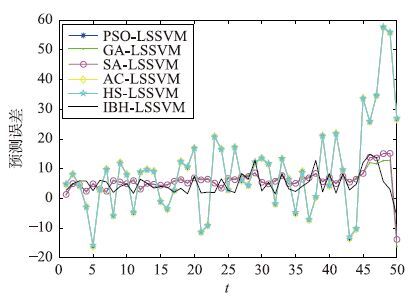
IBH-LSSVM的适应度变化曲线如图 6所示,不同模型的预测结果对比和预测误差曲线分别如图 7和图 8所示,表 1和表 2给出了各预测模型寻优后的参数和性能指标.

|
| 图 6 IBH-LSSVM的适应度变化曲线 Fig. 6 The fitness curve of IBH-LSSVM |

|
| 图 7 动液面混沌序列不同模型预测值的对比 Fig. 7 The comparison of prediction values of different models for the dynamic fluid level series |
|
| 图 8 动液面混沌序列不同模型的预测误差曲线 Fig. 8 Prediction error curves of different models for the dynamic fluid level series |
| 预测模型 | m | τ | γ | σ2 |
| PSO-LSSVM | 2 | 2 | 1 000 | 0.01 |
| GA-LSSVM | 2 | 1 | 196.5 | 9.78 |
| SA-LSSVM | 2 | 1 | 179.3 | 8.30 |
| AC-LSSVM | 3 | 2 | 1 000 | 0.01 |
| HS-LSSVM | 4 | 3 | 809.2 | 0.01 |
| IBH-LSSVM | 1 | 1 | 686.2 | 2.26 |
| 预测模型 | RMSE | MAE |
| PSO-LSSVM | 17.152 7 | 12.488 3 |
| GA-LSSVM | 6.593 0 | 5.932 7 |
| SA-LSSVM | 6.717 3 | 5.976 1 |
| AC-LSSVM | 17.152 7 | 12.488 3 |
| HS-LSSVM | 17.156 4 | 12.462 8 |
| IBH-LSSVM | 5.872 7 | 4.443 7 |
通过以上对比分析,本文所提出的预测模型相比于其它模型具有较好的预测精度,尤为重要的是,IBH-LSSVM预测模型不用设置任何参数,预测结果受外界干扰较小.
7 结论LSSVM在混沌时间序列预测中得到了广泛的应用,所涉及的正则化参数γ、 核函数参数σ2、 嵌入维数m和延迟时间τ4个参数决定了模型的预测精度. 很多优化算法都可以与LSSVM相结合,实现这4个参数的优化选取,但是预测结果一般会受到优化算法参数设置的影响. 对此,本文提出了一种IBH-LSSVM预测模型,该模型中IBH优化算法不需要额外设定任何主观参数,预测结果受主观设定参数影响较小. 为了提高算法搜索的收敛效果,改进算法对可行解的位置更新机制、 “黑洞”的半径、 新“星星”的产生机制以及适应度函数值的计算方式都进行了重新定义. 另外,所采用的基于FLOO的在线校验能够有效杜绝模型训练所存在的过拟合问题. 将其应用于抽油井动液面的短期预测中,对提高石油生产的效率具有十分重要的意义.
| [1] | Dowell J, Weiss S, Hill D, et al. Short-term spatio-temporal prediction of wind speed and direction[J]. Wind Energy, 2014(17): 1945-1955. |
| [2] | Hodge V J, Krishnan R, Austin J, et al. Short-term prediction of traffic flow using a binary neural network[J]. Neural Computing and Applications, 2014, 25(7/8): 1639-1655. |
| [3] | Reid D, Hussain A J, Tawfik H. Financial time series prediction using spiking neural networks[J]. PLoS ONE, 2014, 9(8): e103656. |
| [4] | 唐舟进, 彭涛, 王文博. 一种基于相关分析的局域最小二乘支持向量机小尺度网络流量预测算法[J]. 物理学报, 2014, 63(13): 1-10. Tang Z J, Peng T, Wang W B. A local least square support vector machine prediction algorithm of small scale network traffic based on correlation analysis[J]. Acta Physica Sinica, 2014, 63(13): 1-10. |
| [5] | Chisci L, Mavino A, Perferi G, et al. Real-time epileptic seizure prediction using AR models and support vector machines[J]. IEEE Transactions on Biomedical Engineering, 2010, 57(5): 1124-1132. |
| [6] | Narendra B C, Eswara R B. A moving-average filter based hybrid ARIMA-ANN model for forecasting time series data[J]. Applied Soft Computing, 2014, 23(1): 27-38. |
| [7] | Du W, Leung S Y S, Kwong C K. Time series forecasting by neural networks: A knee point-based multi-objective evolutionary algorithm approach[J]. Expert Systems with Applications, 2014, 41(7): 8049-8061. |
| [8] | 孟庆芳, 陈珊珊, 陈月辉, 等. 基于递归量化分析与支持向量机的癫痫脑电自动检测方法[J]. 物理学报, 2014, 63(5): 1-7. Meng Q F, Chen S S, Chen Y H, et al. Automatic detection of epileptic EEG based on recurrence quantification analysis and SVM[J]. Acta Physica Sinica, 2014, 63(5): 1-7. |
| [9] | Wang Z X, Pei L L. An optimized grey dynamic model for forecasting the output of high-tech industry in china[J]. Mathematical Problems in Engineering, 2014(586284): 1-7. |
| [10] | Askari S, Montazerin N. A high-order multi-variable fuzzy time series forecasting algorithm based on fuzzy clustering[J]. Expert Systems with Applications, 2015, 42(3): 2121-2135. |
| [11] | Suykens J A K, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300. |
| [12] | 田中大, 高宪文, 石彤. 用于混沌时间序列预测的组合核函数最小二乘支持向量机[J]. 物理学报, 2014, 63(16): 1-11. Tian Z D, Gao X W, Shi T. Combination kernel function least squares support vector machine for chaotic time series prediction[J]. Acta Physica Sinica, 2014, 63(16): 1-11. |
| [13] | Zhao L X, Shui P B, Jiang F, et al. Using monitoring data of surface soil to predict whole crop-root zone soil water content with PSO-LSSVM, GRNN and WNN[J]. Earth Science Informatics, 2014, 7(1): 59-68. |
| [14] | Shen M, Chen W N, Zhang J, et al. Optimal selection of parameters for nonuniform embedding of chaotic time series using ant colony optimization[J]. IEEE Transactions on Cybernetics, 2013, 43(2): 790-802. |
| [15] | Sadaei H J, Enayatifar R, Abdullah A H, et al. Short-term load forecasting using a hybrid model with a refined exponentially weighted fuzzy time series and an improved harmony search[J]. International Journal of Electrical Power & Energy Systems, 2014, 62(1): 118-129. |
| [16] | Liu Y, Gao Z L, Li P, et al. Just-in-time kernel learning with adaptive parameter selection for soft sensor modeling of batch processes[J]. Industrial & Engineering Chemistry Research, 2012, 51(11): 4313-4327. |
| [17] | Hatamlou A. Black hole: A new heuristic optimization approach for data clustering[J]. Information Science, 2013, 222(1): 75-184. |
| [18] | 刘毅, 张锡成, 朱可辉, 等. 自适应递推核学习及在橡胶混炼过程在线质量预报的工业应用[J]. 控制理论与应用, 2010, 27(5): 609-614. Liu Y, Zhang X C, Zhu K H, et al. Adaptive recursive kernel learning with application to online quality prediction of industrial rubber mixing process[J]. Control Theory & Applications, 2010, 27(5): 609-614. |
| [19] | Kim H S, Eykholt R, Salas J D. Nonlinear dynamics, delay times, and embedding windows[J]. Physica D: Nonlinear Phenomena, 1999, 127(1): 48-60. |
| [20] | Rosenstein M T, Collins J J, Deluca C J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D, 1993, 65(1): 117-134. |
| [21] | Wang J, Wang W, Wu S. A new support vector machine optimized by simulated annealing for global optimization[J]. International Journal of Precision Engineering and Manufacturing, 2012, 2(1): 8-14. |



