2. 广东工业大学管理学院, 广东 广州 510520
2. School of Management, Guangdong University of Technology, Guangzhou 510520, China
1 引言
随着正倒向随机微分方程理论的不断发展和成熟,带Poisson过程的随机LQ(linear quadratic)问题受到了越来越多专家学者的关注. 带Poisson过程的倒向随机微分方程最先由Tang和Li给出[1]. Wu等[2]给出了一类由Brownian运动和Poisson过程混合驱动的正倒向随机微分方程解存在的唯一性结果,应用这一结果研究了带有Poisson跳跃干扰的线性二次随机最优控制问题,并讨论了一类推广的Riccati方程系统的可解性. Cadenillas[3]研究了带Poisson跳的随机系统的最大值原理,得到了最优控制存在的充要条件,并将结果运用于消费—投资问题. Meng[4]研究了由多维Brownian运动和Poisson随机鞅测度混合驱动的线性二次随机最优控制问题,建立了带跳的倒向随机微分Riccati方程同随机LQ问题与相应Hamilton系统的联系. Haadem等[5]在部分信息结构下研究了无限时域带Poisson跳扩散过程的最大值原理,并给出了其在投资组合选择和消费中的应用.
微分博弈作为对动态系统进行建模和分析的一种非常有用的工具,近年来吸引了很多学者去研究. Starr等[6]最早研究了确定性系统的有限时域线性二次微分博弈问题,得到了Nash均衡点存在的条件. Baser等[7]系统研究了不同信息结构下微分博弈Nash均衡的存在性. 吴臻等[8]研究了一类以Brownian运动和Poisson过程为噪声源的正倒向随机微分方程,得出了开环Nash均衡点的显式形式. An等[9]借助HJBI(Hamilton-Jacobi-Bellman-Isaacs)得出部分信息下随机微分博弈的极大值原理的充要条件. Oksendal等[10]在模型不确定的条件下研究了带跳的正倒向随机微分博弈问题,得到了零和博弈与非零和博弈的最大值原理,并将结果应用于鲁棒最优投资—消费问题中. Shi[11]研究了带跳扩散过程的零和随机微分博弈问题,得到了极大值原理和动态规划二者之间的关系.
另一方面,确定或者随机系统的H∞控制和H2/H∞控制问题引起了学者的关注,并已被广泛应用于各个领域. 在H∞控制和H2/H∞控制问题的众多处理方法中,线性矩阵不等式占据着主流地位,随着博弈理论的深入发展,博弈论方法已成为了一种分析H∞控制和H2/H∞控制的重要方法. 针对H∞控制问题,Limebeer等[12]利用线性二次微分博弈理论研究了确定性时变线性系统的H∞控制问题,给出了该问题存在解的充分必要条件是对应的微分Riccati方程存在解. Zhang等[13]得到了随机H∞控制存在的充分必要条件等价于3个交叉耦合的Hamilton-Jacobi方程有解,并指出有限时域随机H∞控制问题可以转化为求解一个随机微分博弈问题,对应的(uT*,vT*)实际上是博弈问题的鞍点. Zhang等[14]的最新研究将文[13]的结果进行了改进,研究了噪声同时依赖于状态、 控制和干扰的非线性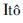 系统的随机H∞控制问题,借助一个Hamilton-Jacobi不等式给出了随机H∞控制策略存在的一个充分条件. 在H2/H∞控制方面,Limebeer等[15]首次利用Nash博弈方法解决了线性确定系统的H2/H∞控制问题,给出了该问题存在解的充分必要条件是一对交叉耦合的Riccati方程存在解. 接着,Chen等[16]提出把随机H2/H∞控制看成一个两人非零和的Nash博弈问题,通过求解Nash均衡点(u*,v*)即可得到随机H2/H∞控制策略. Zhang等[17]利用非合作随机微分博弈得到的极大值原理的必要条件来解决带跳的H2/H∞随机控制问题.
系统的随机H∞控制问题,借助一个Hamilton-Jacobi不等式给出了随机H∞控制策略存在的一个充分条件. 在H2/H∞控制方面,Limebeer等[15]首次利用Nash博弈方法解决了线性确定系统的H2/H∞控制问题,给出了该问题存在解的充分必要条件是一对交叉耦合的Riccati方程存在解. 接着,Chen等[16]提出把随机H2/H∞控制看成一个两人非零和的Nash博弈问题,通过求解Nash均衡点(u*,v*)即可得到随机H2/H∞控制策略. Zhang等[17]利用非合作随机微分博弈得到的极大值原理的必要条件来解决带跳的H2/H∞随机控制问题.
纵观以上文献不难发现,已有的结果多数只考虑了噪声依赖于状态的情形,然而在实际中,存在的噪声不仅依赖于状态,同时也依赖于控制的情形[18, 19]. 本文针对此问题,研究一般意义下由Brownian运动和Poisson过程共同驱动的噪声依赖于状态和控制的线性二次微分博弈. 受文[2]的启发,本文将文[8]的相关结果推广至噪声同时依赖于状态和控制的线性二次微分博弈问题,利用最优控制的最大值原理,研究了非零和博弈的Nash均衡策略和鞍点均衡策略问题,得到了均衡策略的存在条件,并将所得的结果应用于现代鲁棒控制中的随机H2/H∞控制和随机H∞控制问题中,拓展了微分博弈的应用,最后给出一个金融领域投资组合的实际例子.
2 问题描述令(Ω,F,{Ft}t≥0,P)是一个概率空间,F0包含F的所有P-零集,并且Ft+=∩ε>0Ft+ε=Ft,t≥0. 假设信息流Ft由下述2个相互独立的随机过程产生:
(1) 一个标准的布朗运动{W(t)}t≥0;
(2) 一个在R+×ε上的Poisson随机测度N,其中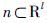 是一个非空的开集,其Borel域为B(ε),它的强度为
是一个非空的开集,其Borel域为B(ε),它的强度为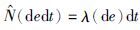 ,且使得
,且使得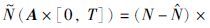 (A×[0,T])t≥0是一个鞅,并使得A∈B(ε)满足λ(A)<∞. λ假定是(ε,B(ε))上的一个σ-有限测度,称之为特征测度.
(A×[0,T])t≥0是一个鞅,并使得A∈B(ε)满足λ(A)<∞. λ假定是(ε,B(ε))上的一个σ-有限测度,称之为特征测度.
给定T>0为一个有限时间区间,我们引入下面记号:
AT: 矩阵或向量A的转置;
Rn: n-维欧氏空间;
Rn×m: 全体n×m阶矩阵构成的集合;
Sn: 全体n×n阶对称矩阵构成的集合;
S+n: 全体n×n阶非负定对称矩阵构成的集合;
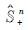 : 全体n×n阶正定对称矩阵构成的集合;
: 全体n×n阶正定对称矩阵构成的集合;
L2n(0,T; Rn): Ft-适应的,[0,T]上Rn-值可测过程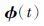 构成的全体,满足
构成的全体,满足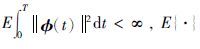 表示数学期望.
表示数学期望.
L∞(0,T; Rn×m): Rn×m-值一致有界函数f: [0,T]→Rn×m构成的全体.
为了简化记号,我们只考虑两个博弈人的情况,N个博弈人的情况类似. 控制系统如下:
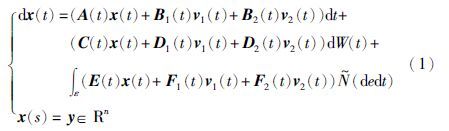
其中,(s,y)∈[0,T)×Rn分别是给定的初始时间和初始状态; v1(t)∈LF2(0,T; Rm1)、 v2(t)∈LF2(0,T; Rm2)是两个容许控制过程,分别表示博弈人1和2的控制策略,且其允许策略空间分别记为U1和U2; A(t)、 C(t)、 E(t)∈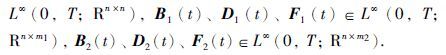 .
.
以J1(v1(·),v2(·))和J2(v1(·),v2(·)),来记博弈人1和2对应的二次性能泛函:
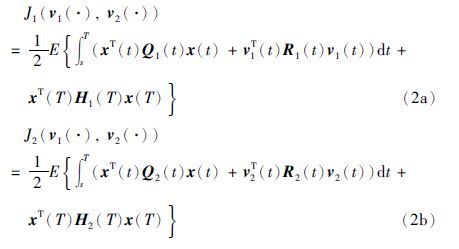
式中,Q1(t)、 Q2(t)∈L∞(0,T; S+n),R1(t)∈L∞(0,T; 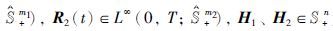 为系数矩阵.
为系数矩阵.
我们的问题是寻找所谓的Nash均衡点(v1*(·),v2*(·))∈U1×U2,使得
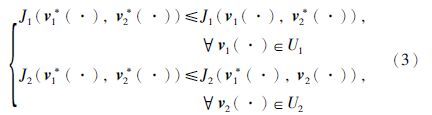
这时两个博弈人的行为是由带有Poisson跳跃的随机过程所描述,我们称此类问题为带Poisson跳的线性二次随机Nash微分博弈,这类博弈问题在经济中有很强的实际应用背景,尤其是在数理金融领域.
3 主要结果下述定理给出了带Poisson跳的两人随机Nash微分博弈问题的主要结果.
定理1 对微分博弈问题(1)~(3),具有下述形式的(v1*(·),v2*(·))是一个Nash均衡点:
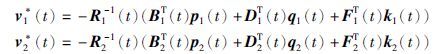
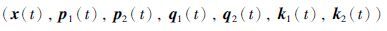 是下述正倒向随机微分方程的解:
是下述正倒向随机微分方程的解:
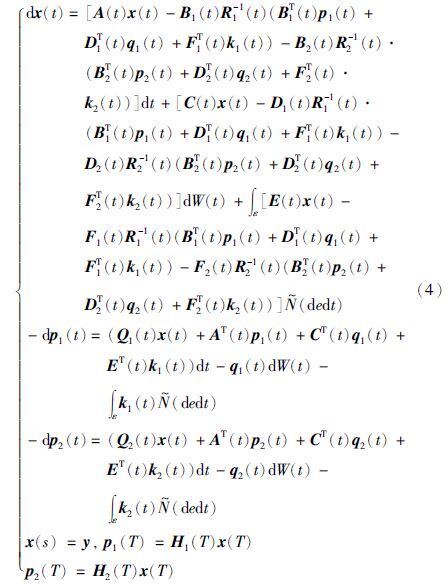
证明 分两步证明,第一步先证明正倒向随机微分方程(4)存在解,第二步再证明(v1*(·),v2*(·))是Nash均衡点.
第一步: 针对上述博弈问题,构造如下的Hamilton函数,分别用H1(t)、 H2(t)表示.
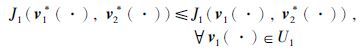
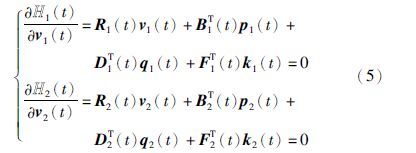
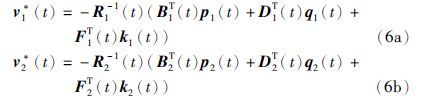
相应的伴随方程为
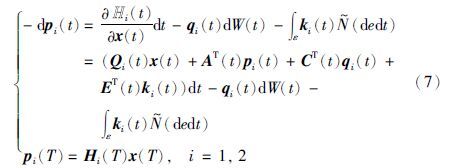
由文[2]知式(7)存在唯一解,从而得到式(4)存在解.
第二步: 我们试图去证明(v1*(·),v2*(·))是带Poisson跳的线性二次随机微分博弈问题的一个Nash均衡点. 我们只需证明
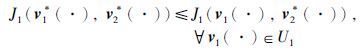
式(3)的另一个不等式可以类似得到. 用x*(t)表示(v1*(·),v2*(·))对应的轨道,则有
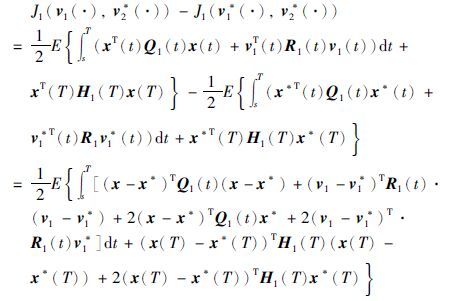
由于H1(T)x(T)=p1(T),对(x(t)-x*(t))Tp(t)应用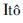 公式,得到
公式,得到
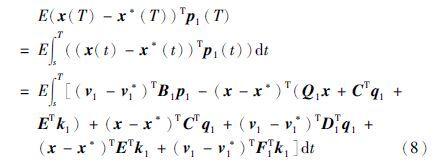
将式(8)的结果代入J1(v1(·),v2*(·))-J1(v1*(·),v2*(·))得:
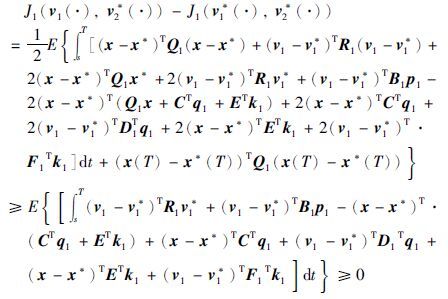
因此(v1(·),v2*(·))是随机Nash微分博弈问题的一个Nash均衡点. 定理1得证.
为了得到状态反馈的Nash均衡解,我们引入下述矩阵Riccati方程:
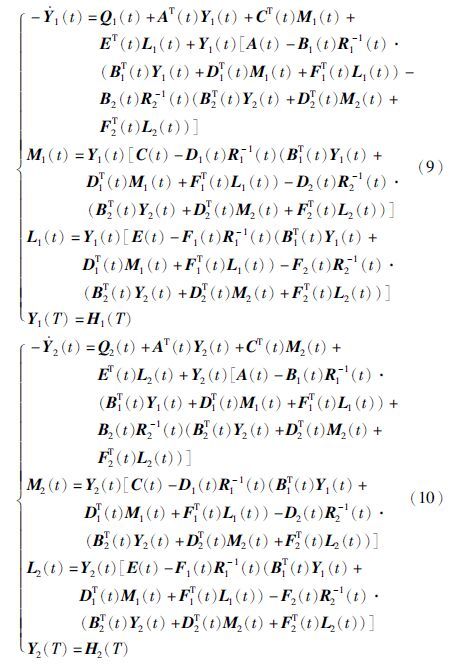
由Tang(2003)的研究可知,以上形式的倒向随机Riccati微分方程的解存在且唯一.
定理2 假设上述矩阵Riccati方程(9)~(10)存在解(Y1(t),M1(t),L1(t))和(Y2(t),M2(t),L2(t)),t∈[0,T],则具有下述形式的状态反馈解(v1(·),v2*(·)):
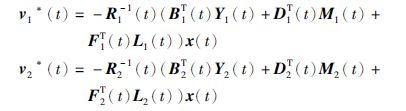
上式是系统(1)~(3)的Nash均衡点,且最优性能泛函分别为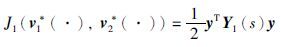 和
和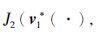
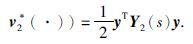
证明 为了得到控制变量vi(·)关于x的反馈表达式,设pi(t)=Yi(t)x(t),qi(t)=Mi(t)x(t),ki(t)=Li(t)x(t)(i=1,2),代入式(4)并经过简单运算即可得到方程(9)~(10). 对Ji(v(·))中的xT(t)pi(t)应用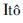 公式即可得到Ji(v*(·)). 定理2证毕.
公式即可得到Ji(v*(·)). 定理2证毕.
在两人Nash博弈中,当一方的收益等于另一方的损失时,我们称该类博弈为零和博弈,此时两博弈人的性能泛函之和为零,用数学表达式描述即为J1(v1(·),v2(·))=-J2(v1(·),v2(·)). 零和博弈在现实中也有着广泛的应用,本部分研究带Poisson跳的线性二次零和随机微分博弈问题.
博弈系统的状态方程约束仍为式(1),为方便表述,将式(1)复制为下式(11)
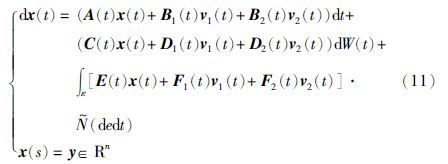
与式(11)对应的性能泛函为
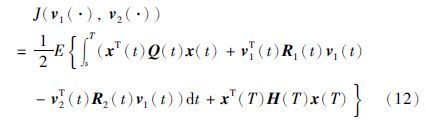
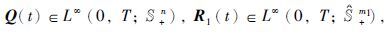
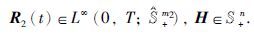
我们的问题是寻找所谓的Nash均衡点(v1(·),v2*(·))∈U1×U2,使得下述不等式成立:
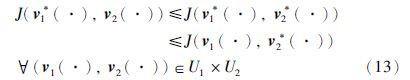
这样的Nash均衡点(v1(·),v2*(·))称为博弈问题的一个鞍点.
定理3 对微分博弈问题(11)~(13),下述形式的(v1(·),v2*(·))是博弈问题的一个鞍点:
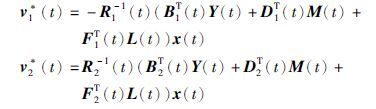
其中,(Y(t),M(t),L(t)),t∈[0,T]是下述Riccati方程的解
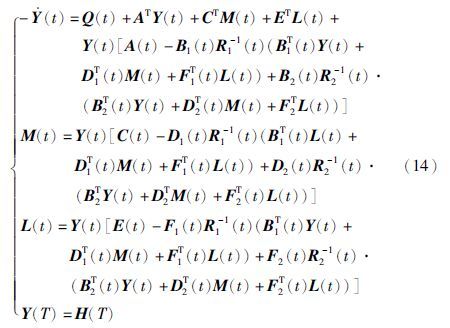
证明 上述博弈问题对应的Hamilton函数为
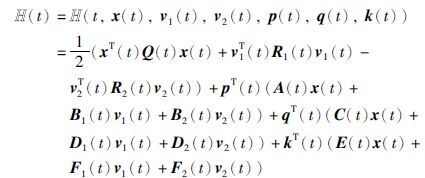
根据最大值原理的必要条件,有
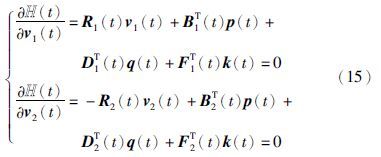
由式(15)得
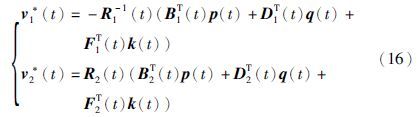
相应的伴随方程为
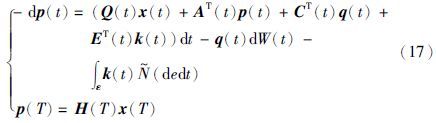
由文[10]知式(17)存在唯一解. 令p(t)=Y(t)x(t),q(t)=M(t)x(t),k(t)=L(t)x(t),对p(t)=Y(t)x(t)
应用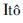 公式,得到
公式,得到
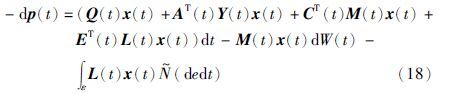
将式(18)代入式(17),整理可得式(14),定理3得证.
5 微分博弈应用于鲁棒控制本部分拟在博弈理论的框架下,利用上述相关结果研究带Poisson跳的噪声同时依赖于状态、 控制和干扰的线性系统的随机H2/H∞控制和随机H∞控制问题.
5.1 随机H2/H∞控制考虑如下的受控系统:
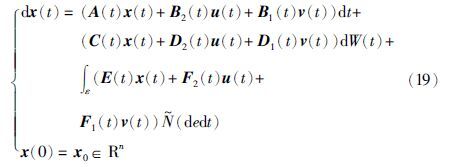
受控输出是一个向量
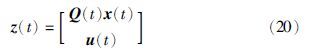
式(19)~式(20)中,x(t)∈Rn为系统状态,u(t)和v(t)分别表示控制输入和外界干扰,系数矩阵A(t)、 C(t)、 E(t)∈L∞(0,T; Rn×n),B1(t)、 D1(t)、 F1(t)∈L∞(0,T; Rn×mv),B2(t)、 D2(t)、 F2(t)∈L∞(0,T; Rn×mu),Q(t)∈L∞(0,T; Sn+). 我们对系数矩阵A(t)等作出这样的假设,目的是保证对任意u(·)∈LF2(0,T; Rmu)和v(·)∈LF2(0,T; Rnv),方程(19)存在唯一的解x(·)∈LF2(0,T; Rn),一般地,称这样满足条件的(x(·),u(·),v(·))是一个容许的组. 下面,我们首先给出有限时间随机H2/H∞控制的定义.
定义1 对任意给定的γ>0,0 <T <∞以及v(·)∈LF2(0,T; Rnv),寻找一个控制u(·)=u*(·)∈LF2(0,T; Rnu),使得
(1) 对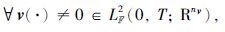 初始状态x0=0的闭环系统(19)的状态过程满足
初始状态x0=0的闭环系统(19)的状态过程满足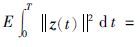
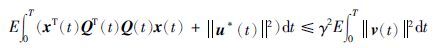
(2) 当最坏外部干扰v*(·)∈LF2(0,T; Rnv)存在时,把v*(·)代入系统(19),u*(·)同时使得性能泛函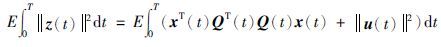 dt达到最小.
dt达到最小.
如果一个容许的控制u(·)∈LF2(0,T; Rmu)只满足(1),那么这个控制u(·)有效地削减了外部干扰的影响,此时我们称它是系统(19)的一个H∞控制,显然,可能有多个H∞控制. 如果(u*(·),v*(·))存在,这意味着u*(·)不仅限制了外部干扰的影响,而且当最坏干扰v*(·)进入系统时,u*(·)使得性能泛函达到最小. 此时,我们就称有限时间随机H2/H∞控制存在一个解.
引入表示干扰抑制水平的标量γ>0,定义如下的两个性能泛函:
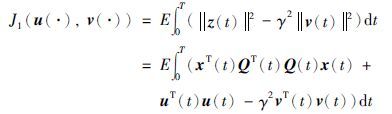
以及
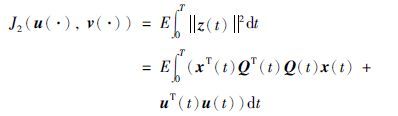
那么随机H2/H∞控制问题等价于寻找如下定义的Nash均衡点(u*(·),v*(·)):
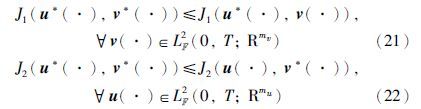
上面的第一个不等式(21)与H∞性能有关,第二个不等式(22)与H2性能有关. 显然,如果Nash均衡点(u*(·),v*(·))存在,那么u*(·)就是我们找的H2/H∞控制器,v*(·)就是最坏干扰. 此时,我们说线性随机H2/H∞控制问题存在解(u*(·),v*(·)).
下面利用第3节中得到的Nash微分博弈的相关结果来求解随机H2/H∞控制问题.
为了方便书写,以下推导省略时间t.
对于上述的随机H2/H∞控制问题,构造相应的Hamilton函数:
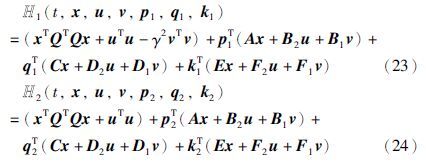
根据最大值原理的必要条件
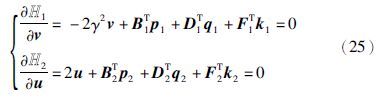
相应的伴随方程为
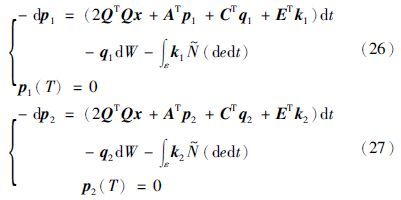
由式(25)得
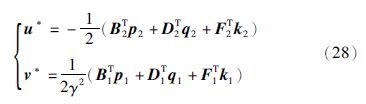
为了得到状态反馈形式的控制策略,在式(26)、 式(27)中令pi=2Yix,qi=2Mix,ki=2Lix(i=1,2). 经过运算得到矩阵(Yi,Mi,Li)(i=1,2)满足下述矩阵Riccati方程
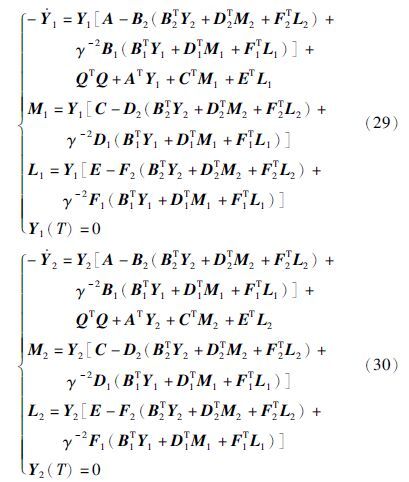
此时的最优控制策略可以表示为
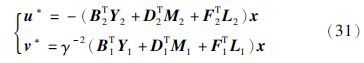
综上所述,我们得到以下定理:
定理4 有限时间随机H2/H∞控制问题存在形如式(31)的解(u*,v*),其中的(Y1,M1,L1)和(Y2,M2,L2)是矩阵Riccati方程(29)~(30)的解.
5.2 随机H∞控制仍考虑式(19)、 式(20)描述的受控系统,给定干扰抑制水平γ>0,定义下述性能泛函
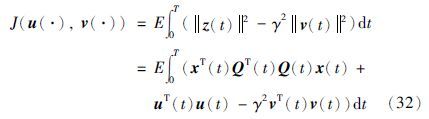
有限时间随机H∞控制的定义如下:
定义2 对受控系统式(19)、 式(20),给定干扰抑制水平γ>0,寻找一个控制u(·)=u*(·)∈LF2(0,T; Rnu),使得在初始条件x0=0下,对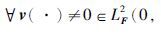 T; Rnv),受控输出z(t)满足
T; Rnv),受控输出z(t)满足
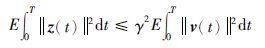
此时的u*(·)即为系统式(19)、 式(20)的随机H∞控制.
针对上述随机H∞控制问题,如果将控制输入u(·)看作博弈人1的控制策略,外界干扰v(·)看作博弈人2的控制策略,则上述随机H∞控制问题即可转换为一个两人零和随机微分博弈问题,博弈人1通过选择u(·)使得性能泛函J(u(·),v(·))最小,而博弈人2通过选择v(·)使得性能指标J(u(·),v(·))最大,而(u*(·),v*(·))即为此博弈问题的鞍点均衡,即(u*(·),v*(·))满足:
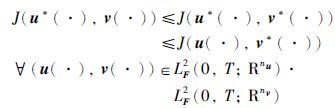
下面利用第4节中得到的两人零和随机微分博弈的相关结果来求解随机H∞控制问题.
Hamilton函数的形式为
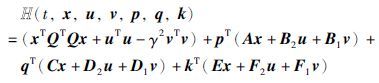
由最大值原理的必要条件得
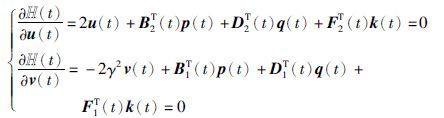
设p(t)=2Y(t)x(t),q(t)=2M(t)x(t),k(t)=2L(t)x(t),利用前文提出的方法,经过简单计算和整理得到随机H∞控制满足:
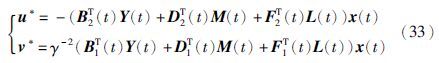
其中,(Y(t),M(t),L(t))满足下述矩阵Riccati方程(省略时间t):
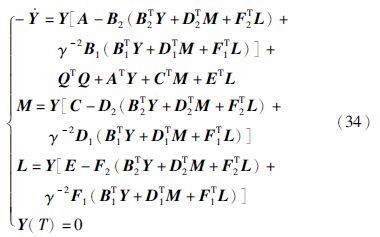
综上所述,我们得到以下定理:
定理5 有限时间随机H∞控制问题存在形如式(33)的解(u*(·),v*(·)),其中的(Y(t),M(t),L(t))是矩阵Riccati方程(34)的解.
6 金融市场中的应用为了说明上述结果的有效性,本小节中,我们给出一个金融市场的投资组合问题,并利用微分博弈的最大值原理求解.
在完备空间(Ω,F,{Ft}t≥0,P),考虑由一种无风险资产和一种风险资产组成的金融市场,对于投资者来说,有两种投资策略可供选择:
(1) 一种是无风险投资(例如把钱存到银行账户),t时刻的价格S0(t)由下式给定: dS0(t)=ρ(t)S0(t)dt,S0(t)>0,ρ(t)是一个确定的函数.
(2) 另一种是风险资产(例如投资股票),t 时刻的价格S1(t)由下式给定:
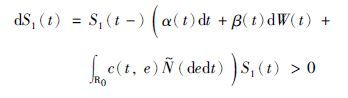
上式中,W(·)表示一维标准布朗运动,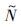 (dedt)=N(dedt)-v(de)是独立于W(·)的Poisson鞅测度. α(t)、 β(t)≠0,c(t,e)≥-1.
(dedt)=N(dedt)-v(de)是独立于W(·)的Poisson鞅测度. α(t)、 β(t)≠0,c(t,e)≥-1.
令π(t)为投资者的投资组合,表示t时刻,投入到风险资产的财富比例,称为投资组合,则投资者的财富过程Yπ(·)满足以下的动态方程:
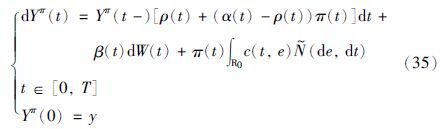
式中,Yπ(0)=y表示投资者的初始财富.
参考Oksendal和Sulem(2007)[20]的研究,我们将上述投资组合选择问题置于微分博弈的框架下进行分析,其中,投资者是博弈的一方,市场是博弈的另一方,投资者通过选择投资组合π来最大化其效用,市场通过选择市场行情,选择概率测度Qθ,最小化投资者的期望效用. 投资者的效用函数为EQθ[U(Yπ(T))]. 其中,U∶[0,∞]→R是递增且二次连续可微的凹函数. 参照Shi[10]的研究,给出由θ决定的概率测度:
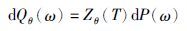
式中的Zθ(t)满足如下的式子:
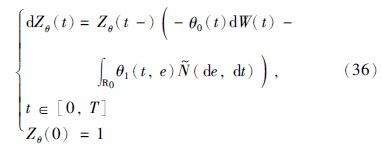
假设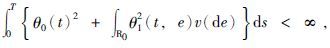 且E[Zθ(T)]=1,则dQθ(ω)=Zθ(T)dP(ω)是等价局部鞅测度.
且E[Zθ(T)]=1,则dQθ(ω)=Zθ(T)dP(ω)是等价局部鞅测度.
我们的目的是寻找这样的(θ,π),使得
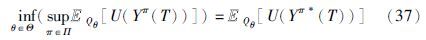
于是,投资者的最优投资策略选择问题即可刻画为市场与投资者之间的一个两人零和随机微分博弈问题: 给定由测度Qθ表示的市场选定的投资“环境”,投资者选择最优投资策略π,最大化其终止时刻财富期望效用. 市场对投资者的选择做出反应,通过选择由测度Qθ表示的“环境”,最小化投资者的最大化期望效用.
我们令x1=X1(t),x2=X2(t),根据上述讨论,构造相应的Hamilton函数,如下:
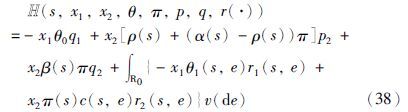
由最大值原理的必要条件,得:
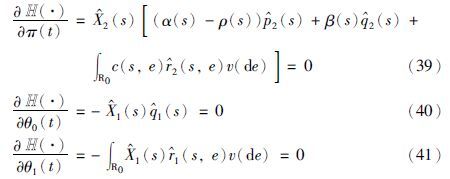
相应的伴随方程为
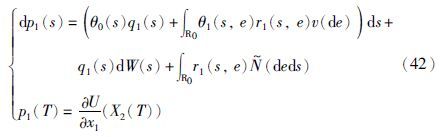
以及
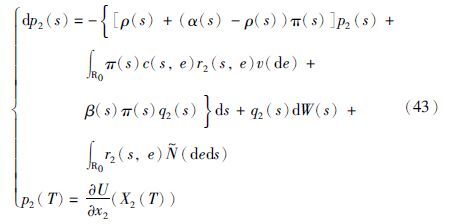
令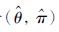 为备选的最优控制(博弈的鞍点),
为备选的最优控制(博弈的鞍点),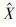 (·)=(
(·)=(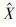 1(·),
1(·),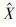 2(·))为相应的状态过程,
2(·))为相应的状态过程,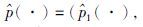
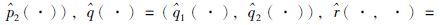
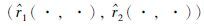 为伴随方程的解.
为伴随方程的解.
假设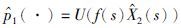 ,其中,函数f(s)满足终端条件f(T)=1. 对
,其中,函数f(s)满足终端条件f(T)=1. 对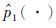 进行
进行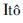 微分,得到
微分,得到
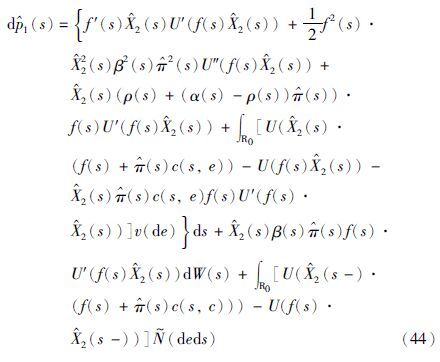
将式(44)的右边代入伴随方程式(42),分别可以得到:
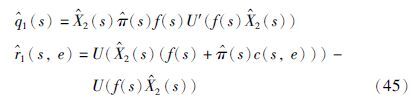
以及
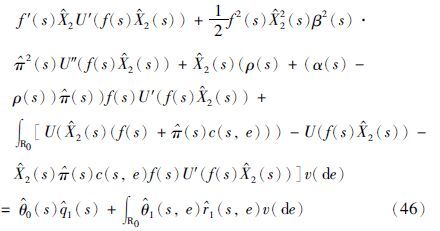
将式(45)代入式(40),有
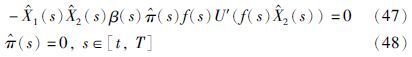
进而得到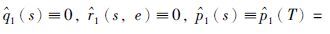
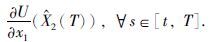
假设
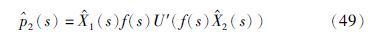
运用与上文相同的处理方法得到
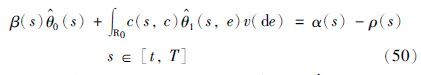
因此,对于投资者来说,最优的投资策略为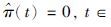 [0,T],此时,市场选择概率测度
[0,T],此时,市场选择概率测度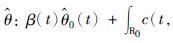
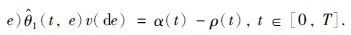
即市场选择满足式(50)的概率测度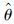 ,以最小化投资者的最大期望收益. 而投资者的最优策略是将所有的资产全部投入到无风险证券中.
,以最小化投资者的最大期望收益. 而投资者的最优策略是将所有的资产全部投入到无风险证券中.
本文针对带Poisson跳扩散过程的随机系统讨论了其线性二次微分博弈问题,包括非零和博弈的Nash均衡策略与零和微分博弈的鞍点均衡策略问题. 利用最优控制的随机最大值原理,得到了Nash均衡策略的存在条件等价于得到的两个交叉耦合的矩阵Riccati方程存在解,鞍点均衡策略的存在条件等价于相应的矩阵Riccati方程存在解. 并将所得的相关结果应用于鲁棒控制中的随机H2/H∞控制与随机H∞控制问题,得到了鲁棒控制策略的存在条件及显式表达. 值得指出的是,本文所考虑的博弈系统,噪声不仅依赖于状态变量,而且依赖于控制变量,因而本文所得的结论在工程实际有着重要的应用价值,尤其在数理金融领域研究不完备市场条件下的投资组合优化问题将发挥更大的作用.
| [1] | Tang S J, Li X J. Necessary conditions for optimal-control of stochastic-systems with random jumps[J]. SIAM Journal on Control and Optimization, 1994, 32(5): 1447-1475. |
| [2] | Wu Z, Wang X R. FBSDE with Poisson process and its application to linear quadratic stochastic optimal control problem with random jumps[J]. Acta Automatica Sinica, 2003, 29(6): 821-826. |
| [3] | Cadenillas A. A stochastic maximum principle for systems with jumps, with applications to finance[J]. Systems & Control Letters, 2002, 47(5): 433-444. |
| [4] | Meng Q X. General linear quadratic optimal stochastic control problem driven by a Brownian motion and a Poisson random martingale measure with random coefficients[J]. Stochastic Analysis and Applications, 2014, 32(1): 88-109. |
| [5] | Haadem S, Oksendal B, Proske F. Maximum principles for jump diffusion processes with infinite horizon[J]. Automatica, 2013, 49(7): 2267-2275. |
| [6] | Starr A W, Ho Y C. Nonzero-sum differential games[J]. Journal of Optimization Theory and Applications, 1969, 3(3): 184-206. |
| [7] | Basar T, Olsder G J. Dynamic noncooperative game theory[M]. 2nd ed.Boston, MA, USA: SIAM, 1999: 266-288. |
| [8] | 吴臻, 于志勇. 带随机跳跃的线性二次非零和微分对策问题[J]. 应用数学和力学, 2005, 26(8): 945-950. Wu Z, Yu Z Y. Linear quadratic nonzero-sum differential games with random jumps[J]. Applied Mathematics and Mechanics, 2005, 26(8): 1034-1039. |
| [9] | An T T K, Oksendal B. Maximum principle for stochastic differential games with partial information[J]. Journal of Optimization Theory and Applications, 2008, 139(3): 463-483. |
| [10] | Oksendal B, Sulem A. Forward-backward stochastic differential games and stochastic control under model uncertainty[J]. Journal of Optimization Theory and Applications, 2014, 161(1): 22-55. |
| [11] | Shi J T. Relationship between maximum principle and dynamic programming for stochastic differential games of jump diffusions[J]. International Journal of Control, 2014, 87(4): 693-703. |
| [12] | Limebeer D J N, Anderson B D O, Khargonekar P P, et al. A game theoretic approach to H∞ control for time-varying systems[J]. SIAM Journal on Control and Optimization, 1992, 30(2): 262-283. |
| [13] | Zhang W H, Chen B S. State feedback H∞ control for a class of nonlinear stochastic systems[J]. SIAM Journal on Control and Optimization, 2006, 44(6): 1973-1991. |
| [14] | Zhang W H, Chen B S, Tang H B, et al. Some remarks on general nonlinear stochastic H∞ control with state, control, and disturbance-dependent noise[J]. IEEE Transactions on Automatic Control, 2014, 59(1): 237-242. |
| [15] | Limebeer D J N, Anderson B D O, Hendel B. A Nash game approach to mixed H2/H∞ control[J]. IEEE Transactions on Automatic Control, 1994, 39(1): 69-82. |
| [16] | Chen B S, Zhang W H. Stochastic H2/H∞ control with state-dependent noise[J]. IEEE Transactions on Automatic Control, 2004, 49(1): 45-57. |
| [17] | Zhang Q X, Sun Q L. A maximum principle approach to stochastic H2/H∞ control with random jumps[J]. Acta Mathematica Scientia, 2015, 35(2): 348-358. |
| [18] | Qian L J, Gajic Z. Variance minimization stochastic power control in CDMA systems[J]. IEEE Transactions on Wireless Communications, 2006, 5(1): 193-202. |
| [19] | Oksendal B. Stochastic differential equations: An introduction with applications[M]. 5th ed. Berlin, Germany: Springer, 1998: 225-241. |
| [20] | Oksendal B, Sulem A. A game theoretic approach to martingale measures in incomplete markets[J]. Pure Mathematics, 2008, 15(24): 1-7. |



