1 引言
电网规划建立在对规划指标(如负荷、 电源、 系统潮流、 市场和技术)进行远景预测的基础上,含有大量不确定因素,由于具有不同的性质和特点,使指标的获取难度加大并对电网规划方案的决策精度有很大影响. 针对这类问题,国内外许多学者对电网规划指标不确定性作了深入研究.
文[1, 2]采用的趋势外推法与时间序列法是通过对历史数据进行归类找出规律,但是要求数据精度要高,并且未考虑随机性和不确定性的影响,对规律性处理也不足; 文[3, 4]采用的人工神经网络法有较好的并行处理能力和较强的非线性映射能力,并且容错性也很好,但是收敛速度太慢并且易陷于局部最小值; 文[5, 6, 7, 8]在层次分析法与盲数处理法中获取信度都采用了构建判断矩阵的方法,其中专家主观性太强,并且针对性强、 自学能力差. 现有的一些方法还有灰色预测法[9, 10]、 小波分析法[11]、 回归分析法[12]、 专家预测法和组合预测法[13]等,由于各种预测方法都存在优劣性,并且每种方法的适用范围也存在局限性,所以只能通过具体问题选择具体方法,而文[14, 15, 16, 17]对不同方法的采用作了分析和总结.
然而,采用概率盒理论对不确定性信息进行预估,不仅适用范围广,而且预估结果精度也较高. 并且在其他领域概率盒对不确定性的处理方面也已有发展,例如文[18]通过建立一个线性质量—弹簧—阻尼系统的概率盒模型,并将不确定数质量、 弹簧和阻尼分别建概率盒,其中有些不确定数的获取是由多种独立信息源分别建概率盒,并通过融合算法的合成获得. 文[19]中,为了建立海堤可靠性模型,分别将影响可靠性的6个不确定性参数建立概率盒,并且与传统概率统计方法比较得出其优越性.
本文利用概率盒能更好解决信息源的未知性、 测量不确定性、 模型不确定性和预估不确定性等一系列问题. 首先,通过分析电网规划不确定性指标的历史数据找出分布规律(均匀分布、 正态分布、 泊松分布、 二项分布等); 然后,针对电网指标不确定性因素提出基于概率盒理论对不确定性建模的研究方法,例如某不确定性指标服从正态分布,通过确定均值与方差这2个参数的范围来限定所有可能的正态分布,并将其限定在一个封闭的图形(盒子)里面,使得不确定信息封闭在一个区间里防止了信息丢失; 最后,通过支持向量机(SVM)[20]分析概率盒建模在处理不确定性方面的优越性,并给出具体的实验结果.
2 电网指标不确定性建模 2.1 概率盒理论及证据理论(D-S)结构体 2.1.1 概率盒
假设有2个非递减函数满足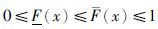 ,其中x∈R. 定义累积分布函数F(x)不能超出范围
,其中x∈R. 定义累积分布函数F(x)不能超出范围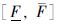 ,而这个范围
,而这个范围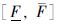 称为概率盒P-box[21],其中
称为概率盒P-box[21],其中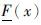 称为F(x)的下边界,
称为F(x)的下边界,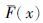 称为F(x)的上边界. 通过对随机变量X的低概率测度
称为F(x)的上边界. 通过对随机变量X的低概率测度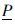 可计算出
可计算出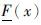 和
和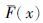 .
.
概率盒下边界: 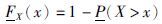
概率盒上边界: 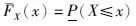
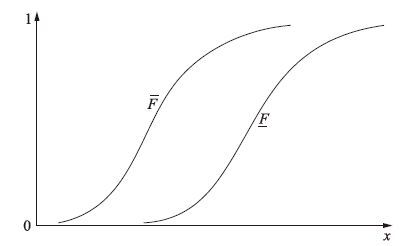
概率盒示意图如图 1所示.
|
| 图 1 概率盒示意图 Fig. 1 Schematic diagram of the P-box |
D-S结构体(DSS)是基于D-S证据理论提出的. 它是由有限个焦元组成,每个焦元是由一个区间和一个信度组成,具体定义如下.
假设一个实数域R,在识别框架上的基本概率m满足如下映射关系:

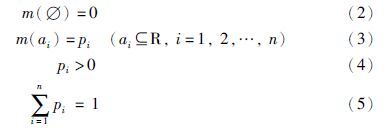
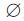 为空集,ai为焦元区间,pi为焦元对应信度值. 对于一个DSS而言,如果命题区间满足b
为空集,ai为焦元区间,pi为焦元对应信度值. 对于一个DSS而言,如果命题区间满足b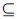 R,并取概率为所有与b有交集的焦元对应的信度之和,称此概率为似然函数(Pls).
R,并取概率为所有与b有交集的焦元对应的信度之和,称此概率为似然函数(Pls).

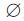 的焦元区间.
的焦元区间.
如果所有命题区间满足b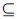 R,并取概率为所有被b所包含的焦元对应的信度之和,称此概率为信任函数(Bel).
R,并取概率为所有被b所包含的焦元对应的信度之和,称此概率为信任函数(Bel).

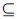 b的焦元区间.
b的焦元区间.
一个DSS基本结构可表示如下:
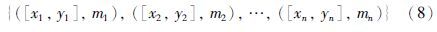
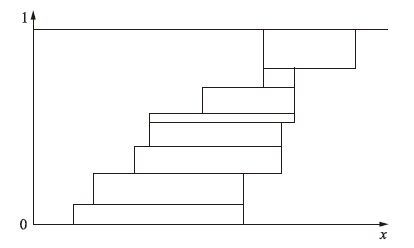
将D-S结构体的各焦元区间的左边界值进行累积叠高可以得到概率盒左边界(即上边界),区间的右边界值进行累积叠高可以得到概率盒右边界(即下边界),如图 2所示. 同样,将概率盒左右边界进行等信度离散化可以近似得到有限个区间和相等的信度值,如图 3所示.
|
| 图 2 概率盒的离散化 Fig. 2 The discretization of the P-box |
|
| 图 3 概率盒的等信度离散化 Fig. 3 Discretization equal reliability of the P-box |
在电网规划方案中对于指标不确定性的类型有很多可能是区间、 分布、 或者不确定数值等,然后通过概率盒建模方法(广义卷积、 转化、 包络、 交集、 加权平均、 合成、 广义去卷积等)可以得到相应的概率盒.
建模方法以包络、 交集、 广义卷积和加权平均为例.
包络: 首先通过概率盒与D-S结构体的关系,将结构体转换成对应的概率盒,如果有n个P-boxes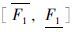 ,
,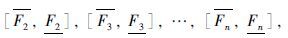 它们通过包络的定义形成的P-box为
它们通过包络的定义形成的P-box为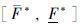 ,其中
,其中

假设有n个区间输入x1,x2,…,xn,对应的包络公式如下:
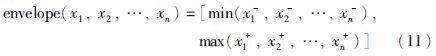
交集: 交集与包络刚好相反,它对应的公式如下:

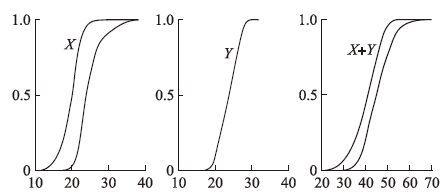
广义卷积: 假设2个独立变量X和Y,其中X服从正态分布μ∈[20, 30],σ∈[3.5,4.5],Y服从对称三角分布min=10,max=30,mod=20; 广义卷积是将变量X和Y分别离散100份之后区间相加,对应概率相乘. 对应的数据如表 1所示,卷积结果如图 4所示.
 | [11.0,15] 0.01 | [11.6,16.7] 0.01 | … | [27.9,35.7] 0.01 | [29.2,37.5] 0.01 |
| [10,11.4] 0.01 | [21,26.4] 0.000 1 | [21.6,28.1] 0.000 1 | … | [37.9,47.1] 0.000 1 | [39.2,48.9] 0.000 1 |
| [11.4,12] 0.01 | [22.4,27] 0.000 1 | [23,28.7] 0.000 1 | … | [39.3,47.7] 0.000 1 | [40.6,49.5] 0.000 1 |
| | | | | | |
| [28.6,30] 0.01 | [39.6,45] 0.000 1 | [40.2,46.7] 0.000 1 | … | [56.5,65.7] 0.000 1 | [57.8,67.5] 0.000 1 |
|
| 图 4 X+Y的广义卷积 Fig. 4 Generalized convolution of X+Y |
加权平均: 如果有n个P-boxes是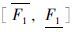 ,
,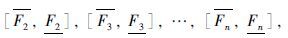 并且对应的权重值分别为w1,w2,…,wn,那么通过加权平均得到的新P-box为
并且对应的权重值分别为w1,w2,…,wn,那么通过加权平均得到的新P-box为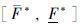 ,其加权公式如下:
,其加权公式如下:
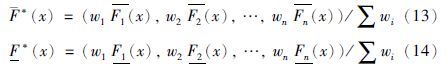
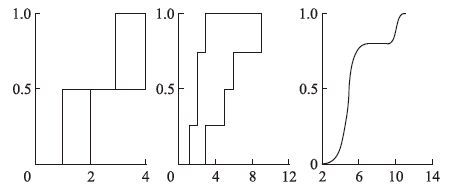
例1 对于2个区间[1, 2]和[3, 4]无加权值,融合所构成的概率盒如图 5(左图)所示.
|
| 图 5 3种不同的融合建盒结果 Fig. 5 Three different results of mixture build P-box |
例2 对于2组D-S结构体D1={([1, 5],0.5),([3, 6],0.5)},D2={([2, 3],0.5),([2, 9],0.5)},采用D-S证据理论融合得到的新的D-S结构体所构成的概率盒如图 5(中图)所示.
例3 对于2个服从μ=5,σ=1与μ=10,σ=0.5的正态分布随机量,对应的权重值分别是5/6和1/6,采用加权平均构成的概率盒如图 5(右图)所示.
同样,电网规划指标多种多样,具体分类如表 2所示. 本文选取的负荷、 电压合格率和线路损耗率3个指标是电网规划方案的底层指标,为了最大限度地保证选用指标的信息不丢失,结合包络建模方法最大边界包裹的特点,建立指标概率盒如下.
| 电网规划指标体系 | ||||||||||||
| 经济性指标 | 技术性指标 | 社会性指标 | 适应性指标 | |||||||||
| 运行经济性 | 建设经济性 | 供电稳定性 | 供电持续性 | 电压合格率 | N-1校验 | 抗大面积停电能力 | 供电负荷量 | 线路损耗率 | 社会环境影响 | 经济适应性 | 政策适应性 | 网架适应性 |
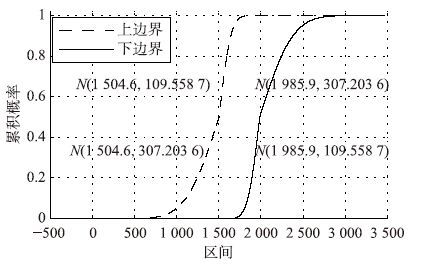
首先,通过收集某地区负荷的历史数据(如表 3),然后进行分析得出其服从正态分布,但是均值和方差是波动变化的,其波动区间为: μ∈[1 504.6,1 985.9],σ∈[109.558 7,307.203 6],于是采用截取累积概率分布曲线N(1 504.6,109.558 7)为概率盒上边界的上半部分,N(1 504.6,307.203 6)为概率盒上边界的下半部分,N(1 985.9,109.558 7)为概率盒下边界的下半部分,N(1 985.9,307.203 6)为概率盒下边界的上半部分形成封闭的包络曲线,即概率盒.
| 时间 | 时刻 | 负荷 | 时刻 | 负荷 | 时刻 | 负荷 |
| 周四 | 0∶00 | 1 463.54 | 8∶00 | 1 951.78 | 16∶00 | 1 955.32 |
| 1∶00 | 1 435.86 | 9∶00 | 2 074.12 | 17∶00 | 2 020.27 | |
| 2∶00 | 1 364.63 | 10∶00 | 1 816.78 | 18∶00 | 2 011.71 | |
| 3∶00 | 1 347.35 | 11∶00 | 1 796.49 | 19∶00 | 2 079.73 | |
| 4∶00 | 1 377.08 | 12∶00 | 1 870.24 | 20∶00 | 2 110.65 | |
| 5∶00 | 1 449.29 | 13∶00 | 1 861.03 | 21∶00 | 2 081.29 | |
| 6∶00 | 1 721.05 | 14∶00 | 1 925.24 | 22∶00 | 1 983.34 | |
| 7∶00 | 1 799.45 | 15∶00 | 1 873.61 | 23∶00 | 1 733.29 | |
| | | | | | | |
| 周日 | 0∶00 | 1 513.09 | 8∶00 | 1 732.57 | 16∶00 | 1 896.13 |
| 1∶00 | 1 456.55 | 9∶00 | 1 702.54 | 17∶00 | 1 826.84 | |
| 2∶00 | 1 430.32 | 10∶00 | 1 867.03 | 18∶00 | 2 113.14 | |
| 3∶00 | 1 389.76 | 11∶00 | 1 857.74 | 19∶00 | 2 078.74 | |
| 4∶00 | 1 476.34 | 12∶00 | 2 010.86 | 20∶00 | 2 004.38 | |
| 5∶00 | 1 573.83 | 13∶00 | 1 678.91 | 21∶00 | 1 949.21 | |
| 6∶00 | 1 688.97 | 14∶00 | 1 902.11 | 22∶00 | 1 735.57 | |
| 7∶00 | 1 789.99 | 15∶00 | 1 845.57 | 23∶00 | 1 712.37 |
将均值与方差两两组合画出累计分布(CDF)得出概率盒如图 6所示.
|
| 图 6 负荷变化不确定性概率盒示意图 Fig. 6 The P-box on the uncertainty of load changes |
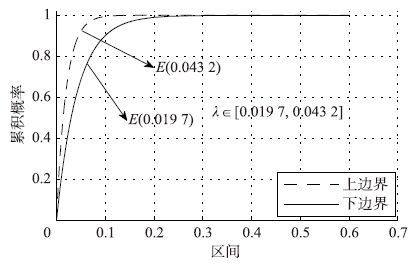
同样,电网线路损耗率通过历史数据进行分析测得其服从指数分布并且分布图形产生波动,得出指数参数波动区间: λ∈[0.019 7,0.043 2],于是采用截取累积概率分布曲线E(0.043 2)为概率盒上边界,E(0.019 7)为概率盒下边界得到相应的概率盒如图 7所示,这样就保证此概率盒包裹该区间的所有可能的累积概率分布曲线.
|
| 图 7 线路损耗率不确定性概率盒示意图 Fig. 7 A probability box on the uncertainty of line loss rate |
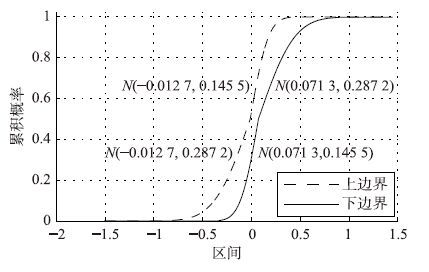
对于某些电网指标,由于采集的频率较快,导致收集的数据量较大,比如说电网技术指标里面电压合格率,此处可以先将收集的数据进行若干次采样,首先将每次采样的点做一个峭度运算(做三次方处理),这样可以将运算后的采样点的特征作为整个数据的特征进行处理,然后分析测试得出几组采样点均服从正态分布,并且收集每组采样点的均值和方差,得出其均值方差所在区: μ∈[-0.012 7,0.071 3],σ∈[0.145 5,0.287 2],采用与符合正态分布的负荷指标一样的方法,得出的概率盒如图 8所示.
|
| 图 8 电压合格率不确定性概率盒示意图 Fig. 8 The P-box on the uncertainty of voltage qualification rate |
最后,由于电网指标种类比较繁多,可能有些指标并不服从某些分布,同样可以通过收集对数据集先进行分组排序(N个分组),求出每个分组的最大值、 最小值和分组概率1/N,然后将每个分组以证据结构体的形式进行累积叠高得出概率盒(原始数据直接建模).
3 实验验证针对电网规划方案对不确定因素影响的适应性,以某区的N种备选方案为例,通过SVM模式识别的方法,先将同一负荷样本数据(分为训练数据与测试数据)分别采用概率盒与传统方法提取特征并为每种方案对负荷变化的适应度进行评测,最后使用Matlab仿真实现.
利用SVM模式识别的过程如下: 首先,将指标历史数据分成初始训练数据和测试数据各50组; 然后,选取核函数与SVM参数,分别用概率盒和传统方法输入训练数据,提取特征进行分类识别训练(方案对负荷变化适应度大于等于80%为合格,用1表示,低于80%为不合格,用0表示),得到训练模型; 最后,输入测试数据得出结果(分类精度和耗时).
其中,概率盒的特征向量提取如下:
(1) 累积宽度;
(2) 对数累积宽度;
(3) 累积区间边界值;
(4) 边界值;
(5) 矛盾区间统计.
而传统方法一般是求均值或者进行简单时域分析(比如去二次方、 三次方)等,本文选取传统方法的特征向量如下:
(1) 取均值;
(2) 求二次方;
(3) 求三次方;
(4) 求中位数.
本文以电网规划指标负荷变化的不确定性为例进行分析(如表 3),通过提取不同的样本容量得出实验结果如表 4、 图 9、 图 10所示.
| 方法 | 样本容量 | 特征向量 | 分类精度/% | 检测速度/(m·s-1) |
| 概率盒 | 1 500 | 累积宽度 | 94.76 | 700 |
| 对数累积宽度 | ||||
| 累积区间边界值 | ||||
| 边界值 | ||||
| 矛盾区间统计 | ||||
| 传统方法 | 1 500 | 取均值 | 89.75 | 917 |
| 二次方 | ||||
| 三次方 | ||||
| 中位数 |
|
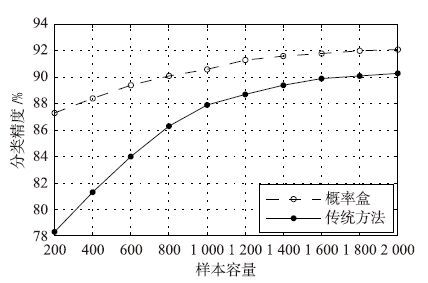
| 图 9 容量—分类精度 Fig. 9 Capacity-classification accuracy |
|
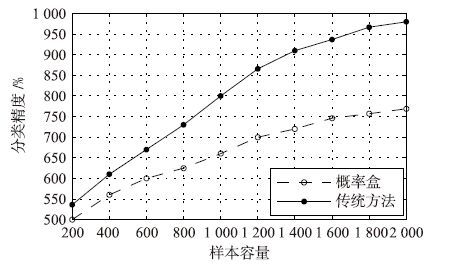
| 图 10 容量—耗时 Fig. 10 Capacity-running time |
由表 4可知,在样本容量一定的情况下,对同样的测试数据和训练数据分别采用概率盒和传统的方法得出的结果不同,实验数据表明在SVM的模式识别下,用概率盒得出的分类精度更高; 同样,不同方法检测速度也不一样,通过实验数据可以看出用概率盒的耗时更短,说明了概率盒比传统方法更快速.
由图 9可知,在样本容量不定的情况下,用概率盒和传统方法得出的分类精度均会上升,但是传统方法对于小样本容量的变化是敏感的(曲线坡度变化较大),而用概率盒得出的曲线较缓,并且得出的精度均高于传统方法,说明概率盒对不确定性不敏感,对实际应用会有更好的实用性.
由图 10可知,在样本容量不定的情况下,样本容量越大耗时越长,而用概率盒所得曲线上升比较平缓,用传统方法所得曲线比较陡峭,说明在数据处理速度方面,用概率盒不仅比传统方法更快,而且对数据容量大的样本有更大的适应性.
综上所述,用支持向量机的模式识别方法测试的结果显示,建概率盒的方法更为优越,不仅封闭了不确定信息,而且能更准确快速的获取指标.
4 结束语在电网规划方面,对电网规划指标不确定性的考虑至关重要. 本文就研究电网指标不确定性给出了具体处理方法,并利用了概率盒的特点及其建模方法封闭不确定性的范围,有效地防止信息丢失,并通过实验验证了此方法的可行性与优越性,表明概率盒建模方法对不确定性的处理更合理,对电网指标不确定的获取更精确.
| [1] | 李栓, 刘莉, 刘阳. 趋势外推法在电力负荷预测中的应用[J]. 沈阳工程学院学报: 自然科学版, 2005, 1(2): 64-65. Li S, Liu L, LiuY. Application of trends extrapolation on the power load forecast[J]. Journal of Shenyang Institute of Engineering: Natural Science Edition, 2005, 1(2): 64-65. |
| [2] | 莫玲. 基于时间序列和人工神经网络的电力系统短期负荷预测[D]. 南昌: 南昌大学, 2006. Mo L. Short term load forecasting in power systems based on time series and artificial neural network[D]. Nanchang: Nanchang University, 2006. |
| [3] | 代林. 基于神经网络的电力负荷预测方法研究及实现[D]. 成都: 电子科技大学, 2012. Dai L. Research and realization based on neural network load forecasting method[D]. Chengdu: University of Electronic Science and Technology of China, 2012. |
| [4] | 李松, 罗勇, 张铭锐. 遗传算法优化BP神经网络的混沌时间序列预测[J]. 计算机工程与应用. 2011, 47(29): 52-55. Li S, Luo Y, Zhang M R. Prediction method for chaotic time series of optimized BP neural network based on genetic algorithm[J]. Computer Engineering and Applications, 2011, 47(29): 52-55. |
| [5] | 徐瑞卿. 基于盲数的市场环境下电网规划[D]. 北京: 北京交通大学, 2007. Xu R Q. Power networks planning under power marketing based on unascertained number[D]. Beijing: Beijing Jiaotong University, 2007. |
| [6] | 蒋国臻. 电网规划综合评价指标体系及方法的研究[D]. 武汉: 华中科技大学, 2009. Jiang G Z. Research on index system and method of network planning comprehensive evaluation[D]. Wuhan: Huazhong University of Science & Technology, 2009. |
| [7] | 翟海保. 多不确定信息的电网灵活规划模型及算法研究[D]. 上海: 上海交通大学, 2007. Qu H B. Models and algorithms of electric power network flexible planning under multi uncertainty[D]. Shanghai: Shanghai Jiaotong University, 2007. |
| [8] | 魏巍, 艾欣. 基于层次分析法的微网客户对电网贡献评价[J]. 华北电力大学学报, 2012, 39(6): 60-64. Wei W, Ai X. The customer credit value evaluation of micro grid based on analytic hierarchy process[J]. Journal of North China Electric Power University, 2012, 39(6): 60-64. |
| [9] | 范鹰, 郭建伟. 灰色模型在电力负荷预测中的应用与改进[J]. 电力需求侧管理, 2006, 8(2): 18-19, 25. Fan Y, Guo J W. The improvement and application of grey model for electric power load forecasting[J]. Power Demand Side Management, 2006, 8(2): 18-19, 25. |
| [10] | 黄清社, 邓文斌, 周保文, 等. 基于灰色模型的等时段序列对电网的负荷预测[J]. 华东电力, 2010, 38(8): 1240-1243. Huang Q S, Deng W B, Zhou B W, et al. Grid load forecasting by grey model-based equal time sequence[J]. East China Electric Power, 2010, 38(8): 1240-1243. |
| [11] | 代怀志. 基于小波变换的电力系统故障信号类型识别研究[D]. 沈阳: 东北大学, 2010. Dai H Z. Research on the fault signals recognition in power systems based on wavelet theory[D]. Shenyang: Northeastern University, 2010. |
| [12] | 刘大利. 迁安市高压配电网规划研究[D]. 北京: 华北电力大学, 2014. Liu D L. Study on the planning of high voltage distribution network in Qian'an city[D]. Beijing: North China Electric Power University, 2014. |
| [13] | 蒋晓艳, 何川. 基于最优组合预测法的电网负荷预测[J]. 水电能源科学, 2010, 28(3): 149-151. Jiang X Y, He C. Application of optimal combined forecasting method to power grid load forecasting[J]. Water Resources and Power, 2010, 28(3): 149-151. |
| [14] | 贺静. 电网规划中不确定性信息处理的研究[D]. 武汉: 武汉大学, 2004. He J. The study of the uncertain factors in the power networks planning[D]. Wuhan: Wuhan University, 2004. |
| [15] | 苏庆新. 区域电力系统超短期负荷预测及网络建模分析[D]. 上海: 东华大学, 2008. Su Q X. Regional electrical power system ultra-short-term load forecasting and network modeling analysis[D]. Shanghai: Donghua University, 2008. |
| [16] | 朱益平. 电网规划不确定性及其处理方法与模型研究综述[J]. 山东电力高等专科学校学报, 2012, 15(2): 1-6. Zhu Y P. A review on study of uncertainty in power grid planning and its processing methods and models[J]. Journal of Shandong Electric Power College, 2012, 15(2): 1-6. |
| [17] | 李勇. 输电网规划中不确定信息处理及动态评判的研究[D]. 保定: 华北电力大学, 2009. Li Y. Research on uncertain information processing and dynamic judgement in transmission network planning[D]. Baoding: North China Electric Power University, 2009. |
| [18] | Tonon F. Using random set theory to propagate epistemic uncertainty through a mechanical system[J]. Reliability Engineering and System Safety, 2004, 85(1/2/3): 169-181. |
| [19] | Ferson S, Tucker W T. Sensitivity in risk analyses with uncertain numbers[R]. Setauket, New York: Applied Biomathematics, 2006. |
| [20] | Ding J M, Du Y, Wang Q X, et al. P-box theory and SVM methods with application in pattern recongition[J]. Applied Mechanics and Materials, 2014, 651/652/653: 472-475. |
| [21] | Ding J M, Du Y, Wang Q X, et al. Fault diagnosis of power transformer based on probability-box theory[J]. Advances in Intelligent Systems Research, 2014, 101: 419-422. |



