1 引言
作业车间调度(job shop scheduling)已被业内证明是NP问题. 随着实际制造环境中紧急件、 工件随即到达等状态频发,使得动态调度问题成为制造系统研究领域的热点之一. 对于动态调度问题,目前有完全反应调度[1, 2](动态在线调度)、 鲁棒性调度[3, 4, 5]和预—反应调度(重调度)[6, 7, 8]三类研究方法. 其中,动态在线调度是指在一定规则下,根据生产系统的局部状态信息,对动态事件实时进行调度的方法,因能对生产过程中的动态事件(如机器故障、 紧急订单到达等)实时反应而受到广泛应用. 熊禾根[9]等针对工序具有相关性、 工件批量到达的动态Job Shop调度问题,设计了有效的组合调度规则进行求解; 文[10]针对动态随机的作业车间,结合调度规则和仿真做了大量实验研究; Sridharan[11]等对动态的作业车间环境,利用规则调度和仿真方法求解,分析了不同规则的调度性能.
总的来说,动态在线调度具有简单明确、 计算复杂度低的优点,是解决作业车间动态调度问题的有效方法之一. 但动态在线调度所依据的调度规则往往只影响调度系统的一个性能指标,没有单一的通用调度规则能同时满足几个调度目标. 为解决这个问题,本文先利用优先级调度规则对作业车间的仿真调度案例进行优化求解,得到满足单个调度目标的最优调度规则,再利用免疫调度算法对选出的最优调度规则建立控制模型,实现调度规则的动态选择,以满足多个调度目标.
2 基于仿真和优先级规则的调度方法 2.1 动态调度问题描述有n个工件(J1,J2,…,Ji,Jn)要在m台机器(M1,M2,…,Mk,Mm)上进行加工,每个工件的加工由一组工序组成,工序必须按照一定的先后顺序在相应的机器上加工; 需要加工的工件随时间推移随机到达车间,且工件的到达时间、 交货期、 各工序的加工时间等并非事先知道,只能随时间的推移逐渐获得. 问题的假设和约束条件如下:
(1) 机器之间没有运输时间,工件在某台机器上完成对应工序的加工后,立刻被运往后续工序的加工机器或离开车间,且工序的安装时间已并入工序加工时间的一部分;
(2) 不同工件的工序之间没有先后约束,同一工件的工序之间有先后顺序约束;
(3) 同一时刻同一台机器只能加工一道工序;
(4) 一旦某道工序在某台机器上开始加工,必须等加工完成后,下一道工序才可以在这台机器上加工;
(5) 同一时刻同一道工序只能被一台机器加工;
(6) 所有工件在0时刻都可以被加工.
2.2 仿真调度案例设计根据作业车间动态调度问题的特点,设计的调度案例如下:
(1) 工件数目(n): 1 000个加工工件随机到达车间,每个工件的属性不同.
(2) 机器数量(m): 作业车间机器数量设置为m=6.
(3) 工件到达时间间隔(Ali-1,i): 任意两个先后到达的工件之间的时间间隔服从指数分布,Ali-1,i= ,λ=
,λ= ; χ为车间利用率,取χ={70%,80%,90%}; ε为机器平均效率,取ε={70%,80%,90%}.
; χ为车间利用率,取χ={70%,80%,90%}; ε为机器平均效率,取ε={70%,80%,90%}.
(4) 工件权重(wi): 服从(0,1)的离散均匀分布,wi~U[0, 1].
(5) 工序数(ni): 每个工件的工序数服从离散均匀分布ni~U[6, 12],故每个工件的平均工序数η=4.
(6) 工序加工时间(pijk): Oij在各机器上的加工时间服从指数分布pijk~e(μ),工序平均加工时间μ=30.
(7) 工件交货期(Di): 采用TWK(total work content)方法[11]设置交货期Di,交货期 ,交货期紧张度因子δ={2,6,8}.
,交货期紧张度因子δ={2,6,8}.
(8) 机器故障: 反映机器故障的主要指标为机器平均修理时间MTTR(mean time to repair)和机器故障平均间隔时间MTBF(mean time between failures)[11, 12].
MTBF: 伽马分布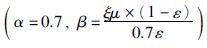
MTTR: 伽马分布 其中,ξ表示机器平均故障水平,取ξ={5,10,15}.
其中,ξ表示机器平均故障水平,取ξ={5,10,15}.
综上,仿真调度案例中涉及的参数如表 1所示,对每个仿真参数设定不同的水平值. m表示机器数量; μ表示工序平均加工时间; δ表示交货期紧张度因子; ε表示机器平均效率; ξ表示机器平均故障水平; χ表示车间利用率.
| 车间结构参数 | 符号 | 取值 |
| 机器数量 | m | 6 |
| 工序平均加工时间 | μ | 30 |
| 交货期紧张度因子 | δ | 2,6,8 |
| 机器平均效率 | ε | 70%,80%,90% |
| 机器平均故障水平 | ξ | 5,10,15 |
| 车间利用率 | χ | 60%,80%,90% |
为对优先级调度规则的调度性能进行评价,选取基于流经时间的指标和基于工件拖期时间的指标[13, 14, 15],如表 2所示.
| 调度目标 | 描述 |
| 最大流经时间最小 | 
|
| 平均流经时间最小 | 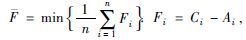 Ci为工件Ji的完工时间,Ai为工件i的到达时间 Ci为工件Ji的完工时间,Ai为工件i的到达时间
|
| 流经时间方差最小 | 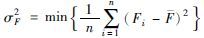
|
| 平均拖期时间最小 | 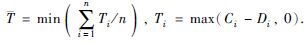 Di为工件Ji的交货期 Di为工件Ji的交货期
|
| 最大拖期时间最小 | 
|
| 拖期时间方差最小 | 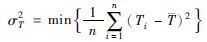
|
| 拖期工件百分比最小 | 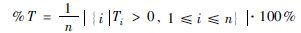 |
采用动态在线调度策略进行求解,根据文[16, 17, 18, 19],选取20种调度规则作为备选集合,如表 3所示. 其中Ai表示工件Ji到达车间的时刻; T为当前时刻; pik表示工件Ji剩余第k道工序的加工时间; wi为工件Ji的权重; Di为工件Ji的交货期; Ci为工件Ji的完工时间; rij表示工件Ji的第j道工序(Oij)到达当前加工机器队列的时刻; pri为工件Ji的优先级.
| 调度规则(20个) | 描述 | 工件i的优先级(pri) |
| FCFS | first come first serve | 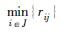
|
| SPT | short processing time | 
|
| EDD | earliest due date | 
|
| EJF | emergent job first | 
|
| RPT_PT_Slack | 
| |
| max((CR-1)×PT,PT) | 
| |
| OSlack | Operation Slack time | 
|
| CR_OSlack | Critical Ratio Operation Slack time | 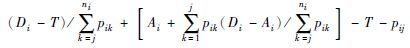
|
| Priority_SPT_Slack | The waiting jobs are divided into 2 classes according to their slack time,the set in which the slack times are all negative has higher priority. In both sets,the jobs are disposed by SPT rule. | |
| PT_StayTime | ratio of processing time to duration in the shop | 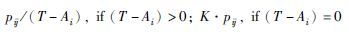
|
| S/RO_PT_α(α=0.1) | 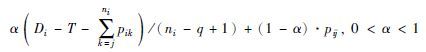
| |
| WINQ | work in the queue of its next operation | 
|
| WINQ+PT | processing time plus work in the queue of its next operation | WINQ+pij |
| AT-RPT | arrival time minus remaining processing time | 
|
| PT+WINQ+AT+Slack | processing time plus WINQ and plus arrival time,then plus Slack | 
|
| PT+WINQ+Slack | processing time plus WINQ and plus Slack | 
|
| PT+WINQ+AT | processing time plus WINQ and plus arrival time | WINQ+pij+Ai |
| 2PT+PW+WTIS/PT | 
| |
| 2PT+LWKR+WTIS/PT | 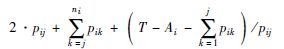 |
利用以上20种调度规则对仿真案例进行调度,采用Matlab进行仿真计算,计算每一种调度规则的性能指标值. 根据车间结构参数情况,可知仿真实验共有81组. 对每一组实验运行20次,取20次的平均值作为结果,记录每个工件的开始加工时间,完工时间,机器累积加工时间等,再计算每一种调度规则对应的性能指标值. 表 4表示仿真参数集为m=6,μ=30,δ=6,ε=80%,ξ=5,χ=80%时,所有调度规则的性能指标值. 数据越小,其对应的调度规则越佳,带“_”的数据为最优值.
| 优先级规则 | 车间结构参数集m=6,μ=30,δ=6,ε=80%,ξ=5,χ=80% | ||||||
| 调度目标 | |||||||
| F | Fmax | σF2 | %T | T | Tmax | σT2 | |
| FCFS | 42.76 | 63.24 | 134.28 | 46 | 69.86 | 48.25 | 488.27 |
| SPT | 2.29 | 150.84 | 220.54 | 2.4 | 42.56 | 66.21 | 5 310.32 |
| EDD | 49.89 | 13.52 | 728.18 | 6.8 | 103.71 | 19.25 | 2 391.82 |
| RPT_PT_Slack | 96.12 | 230.29 | 1 387.19 | 32.2 | 1 028.34 | 1 209.24 | 20 430.34 |
| max((CR-1)×PT,PT) | 39.39 | 33.20 | 291.20 | 3.2 | 1 302.78 | 2 023.2 | 2 833.23 |
| OSlack | 59.37 | 24.29 | 3 385.34 | 33.2 | 5.29 | 12.46 | 9 455.34 |
| CR_OSlack | 52.19 | 47.91 | 1 051.33 | 24.1 | 8.22 | 83.34 | 5 943.35 |
| Priority_SPT_Slack | 39.12 | 60.26 | 782.39 | 33.3 | 48.29 | 413.4 | 37.64 |
| PT_StayTime | 20.22 | 125.32 | 31.35 | 23.2 | 24.43 | 93.92 | 23.47 |
| S/RO_PT_α(α=0.1) | 28.91 | 5.68 | 1 345.92 | 8.3 | 291.12 | 9.27 | 345.42 |
| S/RO_PT_α(α=0.2) | 26.33 | 7.23 | 1 593.48 | 8.1 | 183.42 | 11.38 | 294.46 |
| WINQ | 12.11 | 23.53 | 208.69 | 33.6 | 357.24 | 347.81 | 120.04 |
| WINQ+PT | 1.35 | 12.37 | 86.52 | 25.8 | 182.72 | 178.59 | 1 209.11 |
| AT-RPT | 10.86 | 47.52 | 110.74 | 9 | 18.41 | 98.13 | 99.27 |
| PT+WINQ+AT+Slack | 25.87 | 3.48 | 1.89 | 48.1 | 132.65 | 49.75 | 1 721.27 |
| PT+WINQ+Slack | 5.03 | 35.73 | 83.12 | 40.5 | 74.24 | 28.63 | 88.24 |
| PT+WINQ+AT | 22.34 | 3.16 | 0.79 | 42.5 | 163.77 | 84.56 | 45.76 |
| 2PT+PW+WTIS/PT | 0.00 | 412.12 | 1.06 | 4.2 | 0.10 | 87.29 | 12.73 |
| 2PT+LWKR+WTIS/PT | 3.42 | 372.62 | 28.15 | 1.1 | 7.19 | 81.21 | 84.67 |
由表 4可知: 组合规则的性能指标值优于简单规则. 限于篇幅,将所有仿真结果汇总,列出每个调度目标对应的最优调度规则和相应的仿真参数集,得出表 5~表 11的结果. 注: 表 5~表 11中所有“/”表示“或”,表示参数可选多个水平值. 如表 6中的ε取0.7/0.8,表示它可取0.7或0.8; δ取值为“/”,表示它可取全部水平值.
| parameters of job shop configuration | best dispatching rules | |||
| δ | χ | ε | ξ | |
| 2 | 0.7 | / | / | SPT |
| 2/6 | 0.8 | 0.7 | 5 | |
| 6 | 0.8 | 0.8 | / | 2PT+PW+WTIS/PT |
| 6/8 | 0.8 | 0.9 | 5 | |
| / | 0.9 | / | 10 | 2PT+LWKR+WTIS/PT |
| 2/6 | 0.9 | / | 15 | |
| parameters of job shop configuration | best dispatching rules | |||
| δ | χ | ε | ξ | |
| / | 0.7 | 0.7/0.8 | 15 | S/RO_PT_α(α=0.1) |
| / | 0.8 | 0.7 | 10 | |
| 6 | 0.8 | 0.8 | 5 | PT+WINQ+AT |
| 6 | 0.9 | 0.9 | 10 | |
| 2/6 | 0.7 | 0.8 | 5 | PT+WINQ+AT+Slack |
| 8 | 0.9 | 0.8 | 10 | |
| 2 | 0.7 | 0.7 | 10 | S/RO_PT_α(α=0.2) |
| / | 0.8 | 0.9 | 15 | |
| / | / | 0.8/0.9 | / | |
| parameters of job shop configuration | best dispatching rules | ||
| χ | ε | ξ | |
| 0.8 | 0.7 | 5/10 | PT+WINQ+AT+Slack |
| 0.8 | 0.8/0.9 | 5 | PT+WINQ+AT |
| 0.8 | 0.8 | 10 | 2PT+PW+WTIS/PT |
| 0.9 | 0.9 | 5/10 | |
| 0.7 | / | / | PT_StayTime |
| 0.9 | / | 5 | |
| parameters of job shop configuration | best dispatching rules | |||
| δ | χ | ε | ξ | |
| / | 0.8 | 0.7 | 15 | SPT |
| / | 0.9 | 0.7/0.8 | 15 | |
| 6 | 0.8 | 0.8 | 5 | 2PT+PW+WTIS/PT |
| 6/8 | 0.8 | 0.9 | 5/10 | |
| 8 | 0.7 | 0.9 | 5 | Oslack |
| 6 | 0.7 | 0.8 | 5 | |
| others | max((CR-1)×PT,PT) | |||
| parameters of job shop configuration | best dispatching rules | |||
| δ | χ | ε | ξ | |
| / | 0.7 | 0.7/0.8 | 15 | S/RO_PT_α(α=0.1) |
| 2 | 0.8 | 0.8 | 10 | |
| / | 0.9 | 0.9 | 15 | |
| 2/6 | 0.7 | 0.7 | 10 | S/RO_PT_α(α=0.2) |
| 2 | / | 0.9 | 5/10 | |
| 6 | 0.7 | 0.8/0.9 | 5 | OSlack |
| 8 | 0.7 | 0.8 | 5 | |
| 2/6 | 0.7 | 08. /0.9 | 5 | EDD |
| / | 0.9 | 0.7 | 10 | |
| simulation parameters | best dispatching rules | |||
| δ | χ | ε | ξ | |
| / | 0.7 | 0.9 | 5 | CR_OSlack |
| 8 | 0.8 | / | 5 | |
| 6 | 0.8 | 0.8 | 5 | 2PT+PW+WTIS/PT |
| 2/6 | 0.8 | 0.8/0.9 | 5 | |
| / | 0.7 | 0.7 | 15 | PT_StayTime |
| / | 0.8 | / | 15 | |
| 2/6 | 0.8 | / | 5 | Priority_SPT_Slack |
| / | 0.8 | / | 10 | |
| simulation parameters | best dispatching rules | |||
| δ | χ | ε | ξ | |
| / | 0.7 | 0.7/0.8 | 15 | SPT |
| 2 | 0.7 | 0.7 | 5/10 | |
| 2/6 | 0.8 | 0.7/0.8 | 5/10 | |
| 6/8 | 0.7 | 0.8 | 10 | max((CR-1)×PT,PT) |
| / | 0.7 | 0.9 | 5/10 | |
| 2/6 | 0.7 | 0.9 | 15 | |
| / | 0.7/0.8 | 0.8 | 10 | 2PT+LWKR+WTIS/PT |
| 6/8 | 0.8 | 0.8 | 5 | |
由表 5~表 11可知,对于不同的调度目标,表现最优的调度规则不一样,仿真参数也不一样; 而且,组合规则的性能指标值大多数情况下优于简单规则,说明仿真参数的变化对调度规则的性能表现有明显的影响,且不存在单一的通用调度规则,能满足所有的车间调度环境和调度目标.
3 基于独特型网络的免疫调度算法近年来,针对不同的生产调度问题,已有不同的免疫调度算法能取得较好的效果. 其中,基于免疫网络理论的免疫算法是最常用的免疫优化算法之一[20]. Mori等[21]首次把基于免疫网络理论的免疫算法应用于负载分配和调度问题. Chan等[22]将免疫网络相互作用作为一种选择机制,提出了柔性制造系统分配和调度问题的调度方法. 王也仿[23]、 Qiu[1]把基于免疫网络的免疫算法和调度规则结合来解决调度问题,取得较好效果. 本文提出的免疫调度算法,其实质是利用免疫系统中的独特型网络理论,对前文选出的调度规则建立一种动态控制模型,以满足多目标调度的需求.
3.1 独特型网络模型描述免疫网络理论认为,免疫系统中各细胞不是处于一种独立状态,而是通过自我识别、 相互刺激和抑制构成一个动态平衡的网络[24],其独特型网络模型如图 1所示. 抗体结构中的一个特殊部分为idiotope(独特位),体现了抗体的抗体特征; 抗体的paratope(补位)与抗原的epitope(表位)连接; idiotope(独特位)与其他抗体的paratope(补位)连接,形成一个动态平衡的独特型网络.
3.2 独特型网络模型建立 3.2.1 抗体结构根据独特型网络理论,结合调度规则和调度性能指标,定义的抗体结构如表 12和表 13所示. 抗体由paratope(补位)、 action part(反应部分)和idiotope(独特位)组成. 其中,paratope(补位)代表了与最优调度规则相对应的当前车间状态; action part(反应部分)代表最优调度规则,是抗体结构中的关键部分; idiotope(独特位)代表其他抗体对该抗体的刺激或抑制作用.
| 当前调度目标 | 当前车间结构参数 | 最优调度规则 | (抗体i,亲和力i) | |||||
| χ | m | μ | δ | ε | ξ | |||
| paratope | action part | idiotope | ||||||
| ωi>1 | 调度规则“EJF” | (j,0) |
| paratope | actionpart | idiotope |
为处理加工过程中紧急工件出现的情况,将含有“EJF”(emergent job first)的调度规则作为特殊抗体,特殊抗体独立于模型中的其他抗体. 紧急工件优先级为w>1,只要有紧急工件出现,立刻按“EJF”规则进行调度.
3.2.2 抗原结构独特型网络中的另一个关键成员是抗原,抗原代表系统中新出现的车间状态,抗原结构如表 14所示.
| SPT | OSlack |
| 2PT+PW+WTIS/PT | max((CR-1)×PT,PT) |
| 2PT+LWKR+WTIS/PT | Priority_SPT_Slack |
| S/RO_PT_α(α=0.1) | EDD |
| PT+WINQ+AT | CR_OSlack |
| PT+WINQ+AT+Slack | PT+WINQ |
| S/RO_PT_α(α=0.2) | PT_StayTime |
| WINQ | EJF |
| 调度目标 | 当前仿真参数 | 最优调度规则 | (抗体i,亲和力i) | |||
| χ | δ | ε | ξ | |||
| 流经时间方差最小 | 0.7 | / | / | PT_StayTime |
(抗体1,亲和力1) (抗体i,亲和力i) (抗体n,亲和力n) | |
| 0.9 | / | 5 | ||||
| 拖期时间方差最小 | 0.7 | / | 0.7 | 15 | ||
| 0.8 | / | / | 15 | |||
| paratope | action part | idiotope | ||||
以action part(反应部分)对应的最优调度规则为抗体命名. 由表 5至表 11可知,最优调度规则有15条,故抗体有15个,再加上特殊抗体“EJF”,共有16个抗体.
以抗体“PT_StayTime”为例,说明各抗体的结构. 抗体中的paratope(补位)与抗原中的epitope(表位)匹配,idiotope(独特位)反映了其他抗体对该抗体的刺激或抑制作用,其作用大小以(抗体i,亲和力i)表示.
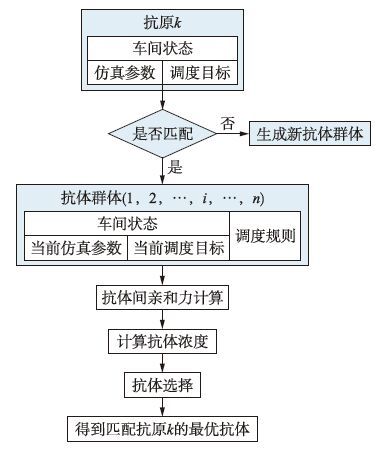
3.3 基于独特型网络的免疫调度算法整个算法的流程如图 2所示.
|
| 图 2 基于独特型网络的免疫调度算法流程图 Fig. 2 Flow chat of immune scheduling algorithm based on idiotypic network |
(1) 抗原与抗体是否匹配. 当系统中出现新抗原时,系统中的抗体迅速搜索,检查抗体的paratope(补位)与抗原的epitope(表位)是否一致,若一致,则初步选择相应的抗体作为备选. 若不一致,则说明系统中的抗体群体不适合该抗原,需重新生成新的抗体群体.
(2) 亲和力计算. 亲和力有两种,一种是抗体与抗原之间的亲和力,一种是抗体间的亲和力. 只有当抗原与抗体匹配时,抗体与抗原之间亲和力值为1; 抗体间亲和力表示系统为某一状态时,抗体间的刺激或抑制作用.
抗体间亲和力值为mijk,表示系统状态为k时,抗体j对抗体i的刺激度或抑制度. 以抗体“PT_StayTime”为例说明,假设车间状态k为: χ=0.8,M=6,δ=6,ε=0.7,ξ=15; 调度目标是拖期时间方差(σT2)最小. 该状态k只与抗体“PT_StayTime”的paratope(补位)相匹配,故抗体“PT_StayTime”为状态k的调度方案. 计算调度规则“PT_StayTime”对应的拖期时间方差(σT2)i和另一个调度规则(抗体j)对应的拖期时间方差(σT2)j,此时,抗体i与抗体j亲和力为mijk=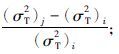 若车间状态k不能与抗体i的paratope(补位)匹配,则mijk=0.
若车间状态k不能与抗体i的paratope(补位)匹配,则mijk=0.
对于所有抗体,有miik=0(抗体对自身没有刺激和抑制作用). 依次计算剩余14个抗体与抗体“PT_StayTime”的亲和力值,形成15×2的亲和力矩阵. 矩阵中的亲和力值越接近1,说明其对应的抗体对抗体“PT_StayTime”的抑制作用就越大. 同理,可得出其他14个抗体中idiotope(独特位)的亲和力矩阵.
(3) 计算抗体浓度. 与抗原匹配的抗体迅速大量增殖,浓度急剧增加,抗体i浓度Ci按下式计算:
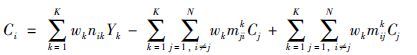
第一项反映了抗原对抗体i的刺激作用. nik是抗体i与抗原k之间的亲和力值,抗原对抗体i的影响与权重wk成比例.
第二项反映了其他抗体对抗体i的抑制作用. Cj为抗体j的浓度,抗体i的表现性能很差(表现最好的是抗体j). mjik为一个很大的正数,抗体i的浓度因此急剧减小,说明抗体i不适合抗原k.
第三项反映了其他抗体对抗体i的刺激作用. 若抗原k对应的最佳抗体是抗体i,抗体j的表现性能远差于抗体i,此时mijk很大,故抗体i会迅速增殖,其浓度会急剧增加.
在不考虑紧急工件的情况下,初始时刻系统中抗体和抗原数量均为0,则Cj=0,Yk=0; 系统中出现抗原k时,Yk=1. 若抗体i能与抗原k相匹配,则Ci=1,nik=1,否则为0. 只有与抗原匹配的抗体,其浓度才会大于0. 抗体的浓度值按浓度计算式不断更新.
(4) 选择抗体. 选择最优抗体进行调度. 若车间状态不变,则抗原和抗体处于一种稳定状态,按照轮盘赌算法选择抗体,浓度越大的抗体,被选中的概率越大. 抗体群体为N={1,2,…,i,…,15},抗体i被选择的概率为

若系统中出现了紧急工件到达的情况,此时抗体“EJF”会迅速大量增殖,达到很高的浓度,故EJF规则能及时对紧急工件进行处理,其他工件仍由对应的抗体进行调度. 车间状态一旦发生变化,立刻清零所有抗体和抗原,回到调度初始状态. 更新后的调度系统根据新的调度问题产生新的抗体、 抗原.
4 仿真实验设计
由于动态调度问题没有标准算例,设计1 000个工件、 6台机器的测试数据集,测试数据集中包括1 000个随机产生的测试样本; 每个样本的仿真参数集和调度目标同1.2节和1.3节. 为测试算法解决多目标调度问题的有效性,将算法与其他20条优先级调度规则分别比较,故有21种调度方法. 调度方法s的整体性能: 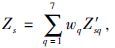 其中,wq为目标q的权重,随机生成; Z′sq为方法s对应的目标值,按标准化处理式
其中,wq为目标q的权重,随机生成; Z′sq为方法s对应的目标值,按标准化处理式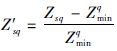 计算; Zsq表示方法s处理目标q的性能指标; Zmins表示单目标q在21种调度方法对应的最优值; Zs值越小,则调度方法s的整体性能越好. 若Zs=0,表示对任意一个目标q,均有Zq=Zminq,说明方法s对所有目标表现均为最佳.
计算; Zsq表示方法s处理目标q的性能指标; Zmins表示单目标q在21种调度方法对应的最优值; Zs值越小,则调度方法s的整体性能越好. 若Zs=0,表示对任意一个目标q,均有Zq=Zminq,说明方法s对所有目标表现均为最佳.
利用Matlab对测试数据集进行仿真运算. 将21种调度方法在测试样本上运行,每个样本运行20次,仿真到达稳态后搜集仿真数据,取平均值为结果,每个测试样本中,对21种调度方法进行比较. 限于篇幅,举一个例子说明. 若车间状态为随机生成χ=0.8,M=6,δ=6,ε=0.7,ξ=15,调度要满足流经时间方差最小、 拖期时间方差最小2个目标,随机生成两个目标的权重分别为0.7和0.3,经过仿真计算,得到如图 3所示的结果. 图 3(a)表示调度目标为流经时间方差最小,所有调度方法的性能指标值; 图 3(b)表示调度目标为拖期时间方差最小,所有调度方法的性能指标值.

|
| 图 3 某种车间状态下21种调度方法的性能指标值 Fig. 3 The performance of 21 scheduling methods under one job shop situation |
由图 3(a),目标“流经时间方差最小”在21种调度方法下的最优值为免疫调度算法对应的Zmins=39,除此之外,调度方法PT-StayTime的性能指标值最优,其对应的目标值为Z′sq=45-3939=639,IM调度算法对应的目标值为Z′sq=0,其他调度方法的目标值均大于0.
由图 3(b),目标“拖期时间方差最小”在21种调度方法下的最优值为IM调度算法对应的Zmins=12,除此之外,调度方法PT-StayTime的性能指标值最优,其对应的目标值为 IM调度算法对应的目标值为Z′sq=0,其他调度方法的目标值均大于0.
IM调度算法对应的目标值为Z′sq=0,其他调度方法的目标值均大于0.
综上,由图 3,调度方法PT-StayTime对于两个目标的总体性能为:  IM方法对于两个调度目标的总体性能为: Zs=0,说明IM调度算法对“流经时间方差最小”和“拖期时间方差最小”两个调度目标均为最优,因此在解决这两个调度目标时,应选择IM调度算法.
IM方法对于两个调度目标的总体性能为: Zs=0,说明IM调度算法对“流经时间方差最小”和“拖期时间方差最小”两个调度目标均为最优,因此在解决这两个调度目标时,应选择IM调度算法.
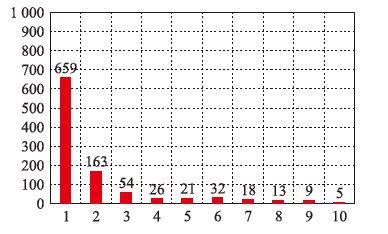
同理,在1 000个测试样本中,将基于独特型网络的免疫调度算法在21种调度方法中的累计频数情况列出,表示为图 4. 显然,在动态的车间环境中,与其他20种规则调度方法相比,免疫调度算法被选中了659次,说明设计的免疫调度算法远远优于其他单个优先级规则调度方法,展现了算法处理多目标动态调度问题的效率和有效性.
|
| 图 4 免疫调度算法的频数累积 Fig. 4 The cumulative frequency of immune algorithm |
利用动态在线调度和基于独特型网络的免疫算法,对动态环境下的作业车间多目标调度问题进行了研究. 针对工件动态随机到达作业车间的情形,设计大量仿真调度案例,并利用优先级调度规则对案例进行调度安排. 经过大量仿真实验,选出了满足单个调度目标的最优调度规则; 为解决调度规则不能适应动态变化的车间环境的问题,设计了基于独特型网络理论的免疫调度算法,仿真测试数据表明,该免疫调度算法能够有效地控制调度规则,使其满足多个调度目标,有效地解决了动态环境下作业车间的多目标调度问题.
| [1] | Qiu X N, Lau H Y K. An AIS-based hybrid algorithm with PDRs for multi-objective dynamic online job shop scheduling problem[J]. Applied Soft Computing, 2013, 13(8): 1340-1351. |
| [2] | 林屾. 动态不确定条件下橡胶硫化车间生产调度问题研究[D]. 青岛: 青岛科技大学, 2010. Lin C. Study on production scheduling of rubber vulcanization workshop in dynamic and uncertain environments[D]. Qingdao: Qingdao University of Science &Technology, 2010. |
| [3] | 丁然. 不确定条件下鲁棒性生产调度的研究[D]. 济南: 山东大学, 2006. Ding R. Study of robust production scheduling under uncertainty[D]. Ji'nan: Shandong University, 2006. |
| [4] | 张先超, 周泓. 单机鲁棒调度多目标优化方法[J]. 计算机集成制造系统, 2013, 19(5): 2459-2466. Zhang X C, Zhou H. Multi-objective optimization for robust single-machine scheduling[J]. Computer Integrated Manufacturing System, 2013, 19(5): 2459-2466. |
| [5] | 刘琳, 谷寒雨, 席裕庚. 加工时间不确定的Just-in-time单机鲁棒调度[J]. 控制与决策, 2007, 22(10): 1151-1154, 1159. Liu L, Gu H Y, Xi Y G. Robust scheduling in a Just-in-time single machine system with processing time uncertainty[J]. Control and Decision, 2007, 22(10): 1151-1154, 1159. |
| [6] | 庞新富, 俞胜平, 张志宇, 等. 炼钢—连铸生产优化重调度方法[J]. 系统工程学报, 2010, 25(1): 98-103, 144. Pang X F, Yu S P, Zhang Z Y, et al. Optimal rescheduling method for steel making-continuous casting[J]. Journal of Systems Engineering, 2010, 25(1): 98-103, 144. |
| [7] | 上官春霞, 周泓, 师瑞峰, 等. 作业车间排序重调度问题及其改进修复约束满足算法[J]. 计算机集成制造系统, 2008, 14(4): 1742-1751, 1773. Shangguan C X, Zhou H, Shi R F, et al. Flow shop rescheduling problem and its improved repair-based constraint satisfaction algorithm[J]. Computer Integrated Manufacturing System, 2008, 14(4) 1742-1751, 1773. |
| [8] | 单晖. 基于实时工况的Job Shop动态随机重调度方法研究[D]. 合肥: 合肥工业大学, 2008. Shan H. Research on method of Job Shop dynamic stochastic rescheduling based on real-time status[D]. Hefei: Hefei University of technology, 2008. |
| [9] | 熊禾根, 李建军, 孔建益, 等. 考虑工序相关性的动态Job shop调度问题启发式算法[J]. 机械工程学报, 2006, 42(1): 50-55. Xiong H G, Li J J, Kong J Y, et al. Heuristic method for dynamic Job Shop scheduling problem with operation relativity[J]. Chinese Journal of Mechanical Engineering, 2006, 42(1): 50-55. |
| [10] | Kutanoglu E, Sabuncuoglu I. Experimental investigation of iterative simulation-based scheduling in a dynamic and stochastic job shop[J]. Journal of Manufacturing Systems, 2001, 20(4): 264-279. |
| [11] | Sridharan R, Vinod V. Dynamic job-shop scheduling with sequence-dependent setup times simulation modeling and analysis[J]. International Journal of Advanced Manufacturing Technology, 2008, 36(3): 355-372. |
| [12] | Rangsaritratsamee R, Ferrell W G, Kurz M B. Dynamic rescheduling that simultaneously considers efficiency and stability[J]. Computers & Industrial Engineering, 2004, 46(3): 1-15. |
| [13] | 高亮, 张国辉, 王晓娟. 柔性作业车间调度智能算法及其应用[M]. 武汉: 华中科技大学出版社, 2012. Gao L, Zhang G H, Wang X J. The flexible job-shop scheduling intelligent algorithm and its application[M]. Wuhan: Huazhong University of Science and Technology Press, 2012. |
| [14] | Dominic P D D, Kaliyamoorthy S, Kumar M S. Efficient dispatching rules for dynamic job shop scheduling[J]. International Journal of Advanced Manufacturing Technology, 2004, 24(1): 70-75. |
| [15] | Sels V, Gheysen N, Vanhoucke M. A comparison of priority rules for the job shop scheduling problem under different flow time and tardiness related objections[J]. International Journal of Production Research, 2012, 50(8): 4255-4270. |
| [16] | Lawrence S R, Sewell E C. Heuristic, optimal, static, and dynamic schedules when processing times are uncertain[J]. Journal of Operations Management, 1997, 15(5): 71-82. |
| [17] | Subramaniam V, Ramesh T, Lee G K, et al. Job shop scheduling with dynamic fuzzy selection of dispatching rules[J]. International Journal of Advanced Manufacturing Technology, 2000, 16(2): 759-764. |
| [18] | 李宁. 基于仿真的生产调度问题研究[D]. 兰州: 兰州理工大学, 2014. Li N. Research on production scheduling based on simulation[D]. Lanzhou: Lanzhou University of Technology, 2014. |
| [19] | 莫宏伟, 左兴权. 人工免疫系统[M]. 北京: 科学出版社, 2009. Mo H W, Zuo X Q. Artificial immune system[M]. Beijing: Science Press, 2009. |
| [20] | Fukuda T, Mori K, Tsukiyama M. Immune networks using genetic algorithm for adaptive production scheduling[C]//The 12th IFAC Triennial World Congress. Kington, UK: IFAC, 1993. |
| [21] | Chan F T S, Swarnkar R, Tiwari M K. Fuzzy goal-programming model with an artificial immune system approach for a machine tool selection and operation allocation problem in a flexible manufacturing system[J]. International Journal of Production Research, 2005, 43(19): 4147-4163. |
| [22] | 王也仿, 杨建国. 基于规则与生物免疫机理的多目标作业调度方法应用研究[J]. 东华大学学报: 自然科学版, 2005(04): 52-56. Wang Y F, Yang J G. Study on scheduling method and application with multi-objective based on rule and immune mechanism[J]. Journal of Donghua University: Natural Science Edition, 2005(04): 52-56. |
| [23] | Jerne N. Towards the network theory of the immune system[J]. Annals of Immunology, 1974, 125(C): 373-389. |




