1 引言
近年来，分数阶建模在科学工程的很多领域都得到了应用. 分数阶模型能够更加精确地描述现实中的一些系统，如岩石蠕变特性[1, 2]、 系统阻抗[3, 4]、 热传导系统[5, 6]等. 如何建立系统的分数阶模型受到了越来越多的学者的关注. 分数阶系统的建模可以分为时域和频域两个方面，文[7, 8, 9]对时域中分数阶模型的建立进行了研究. 由于分数阶微积分算子的长记忆特性，时域方法通常需要大量的历史数据和复杂的计算，而频域方法则可以较好地避开这一问题. 文[10, 11, 12, 13, 14, 15]对分数阶系统的频域辨识进行了研究. 文[10, 11, 12]应用最小二乘法对分数阶系统进行了频域辨识，但均需要已知分数阶系统的阶次且都未考虑噪声的影响. 文[13]和文[14]应用智能优化算法辨识系统的阶次参数，同时应用最小二乘拟合方法辨识分子分母多项式系数. 虽然文[13, 14]提出的辨识方法可以对分数阶系统进行整体辨识，但是在有色噪声的环境下，往往不能得到满意的结果. 文[15]采用极大似然法对噪声环境下的分数阶系统进行了辨识，取得了良好的辨识效果，但极大似然法对噪声的分布是有一定的要求的.
本文基于已有的参考文献的成果，研究了频域中噪声环境下的分数阶系统的整体辨识. 频域辨识具有容易去除高频噪声、 数据量较少等优点，文[16]详细介绍了最小二乘法、 极大似然法、 辅助变量法等辨识方法在频域辨识中的应用. 其中，辅助变量法对噪声的模型结构没有要求，能够较好地抑制各频段的噪声，已在整数阶系统的频域辨
识中得到了成功的应用[17, 18, 19]. 本文的方法是将辅助变量法和粒子群算法相结合. 文[20]同样采用了辅助变量法对分数阶系统进行辨识，本文的方法与其最主要的不同体现为： 文[20]假定同元次分数阶系统的公因子阶次已知，本文的方法则可以同时辨识出系统的阶次参数. 另外，在辅助变量方法的应用上，文[20]利用欧拉公式对系统频率响应的虚部和实部进行分离，需要大量的三角函数计算，本文直接对其进行分离，减少了计算过程中的误差； 文[20]应用的是一次完成算法，当观测数据较多或观测阵的行列式较小时，往往会给计算带来较大的误差，本文推导了频域中分数阶系统辅助变量法的递推形式，在求解过程中避免了矩阵的求逆运算，可以避免这一缺陷.
2 分数阶系统的递推辅助变量辨识 2.1 分数阶系统分数阶系统是建立在分数阶微积分方程基础上的数学模型，是对整数阶模型的推广. 其一般形式为
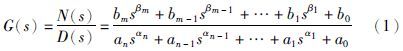
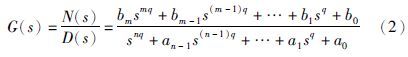
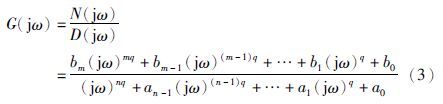
本文对同元次分数阶的辨识方法进行了详细的阐述，之后通过一个辨识实例将辨识方法扩展到一般分数阶系统的辨识上.
2.2 递推辅助变量法辅助变量法可以视为基本最小二乘法的延伸，用来克服基本最小二乘法在有色噪声环境下不能够得到参数的无偏估计的缺点. 现考虑如式(4)所示带有噪声的同元次分数阶系统：
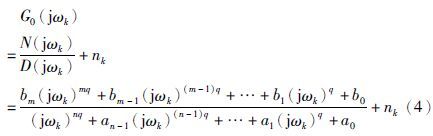
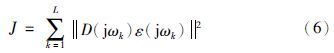
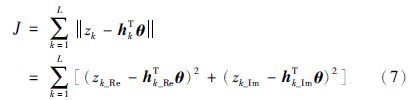
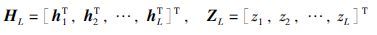
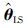，如式(8)所示：
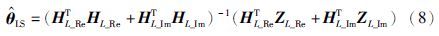
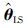的无偏性，引入以下变量：
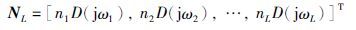
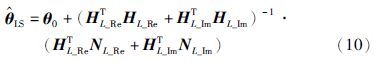
由式(9)和式(10)可以看到，一般情况下，即使nk为白噪声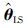，也并不是θ0的无偏估计. 现引入辅助变量hk*，并令HL*=[h1*T，h2*T，…，hL*T]T，当式(11)成立，得到的辅助变量参数估计
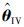即为θ0的无偏估计，如式(12)所示.
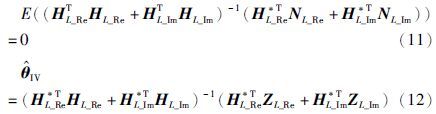
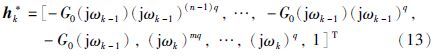
式(12)为辅助变量法的一次完成算法，为了避免在矩阵求逆过程中带来的计算误差，应用式(14)和式(15)所示运算的关系式(式(14)和式(15)为数据实部的运算关系，数据虚部的运算与实部相同)，同时应用式(16)所示的矩阵反演公式，可以推导得到式(17)～(19)所示的辅助变量法的递推格式：
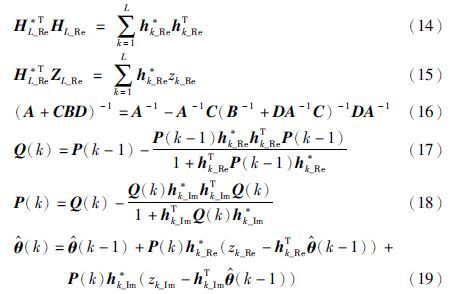
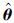的初始值分别设置为1 000I和0.001.
2.3 仿真实例为了验证本节辨识算法的有效性，对以下系统进行辨识：
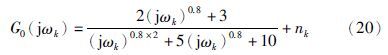
为了能够更好地表现系统的频率特性，所选取的实验频段应该能够包括系统频率特性的主要拐点. 这里实验频率点ωk在[0.1，100]之间按对数均匀取值，观测点数L取为1 000. 噪声nk是均值为零的复随机噪声，信噪比SNR(signal to noise ratio)为20. 由于噪声是随机变量，因此由不同批次的测量数据得到的参数估计值同样为随机变量. 为了对本文的辨识方法的统计性质有更好地了解，本文通过仿真，得到了10 000组观测数据. 图 1为递推辅助变量法10 000次辨识结果的频率直方图，图 2为递推最小二乘法在同样的10 000组数据下得到的辨识结果的频率直方图. 由图中可以看到，递推辅助变量法在所有参数上得到的结果基本都是无偏的，递推最小二乘法在参数a1、 a0和b0上的偏差较大. 但同时，也可以看到，由于辅助变量的引入，辅助变量法在a1、 a0和b0上辨识结果的分散度要大于最小二乘法. 由于hk*和hk之间的相关度必然要小于hk和hk之间的相关度，因此这是不可避免的现象.
|
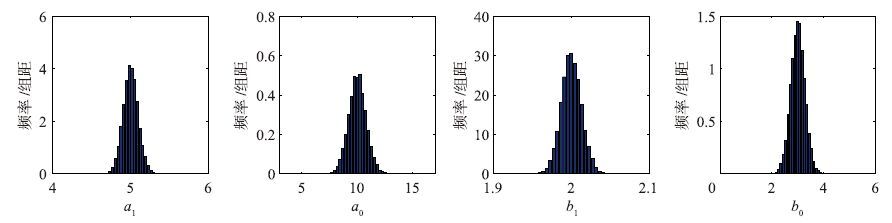
| 图 1 递推辅助变量法辨识结果 Fig. 1 Results of recursive instrumental variables method |
|
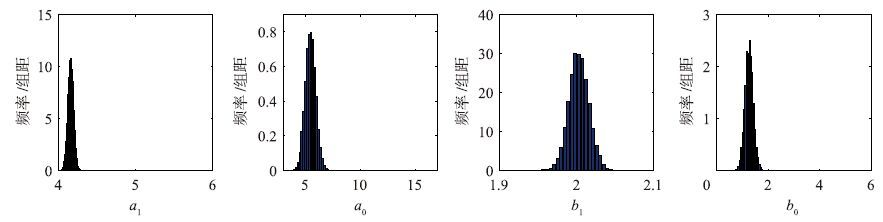
| 图 2 递推最小二乘法辨识结果 Fig. 2 Results of recursive least squares method |
第2节讨论了当式(4)所示系统的公因子阶次q已知时的参数辨识方法. 本节将对q未知时的系统进行整体的辨识. 对于式(5)和式(6)，q均为非线性的，本文采用粒子群优化算法对其进行寻优，同时结合递推辅助变量法得到θ的估计值，进而完成对系统的整体辨识.
3.1 粒子群优化算法粒子群优化算法是一种高效的群智能优化算法，由于其原理简单、 易于实现、 不要求待优化问题的可微性等，已被广泛应用于各种领域. 设群体的规模为M，群体中的每个粒子代表着D维寻优空间中的一个潜在解，具有由待优化函数决定的适应值. xi=[xi1，xi2，…，xiD]和vi=[vi1，vi2，…，viD]分别是粒子i的位置矢量和速度矢量，f(xi)是粒子i的目标函数值. pi=[pi1，pi2，…，piD]为第i个粒子迄今为止搜索到的最优位置，pg=[pg1，pg2，…，pgD]为整个群体迄今为止搜索到的最优位置. 在进化过程中的任意t+1代，粒子i的第d维速度和位置根据式(21)、(22)更新：
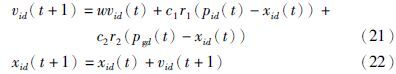
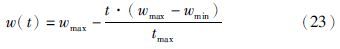
在任意t+1代，当群体中的所有粒子完成速度和位置的更新后，计算每个粒子的适应值，并按照式(24)和式(25)更新每个粒子的个体极值和群体的全局极值，为群体在下一代的更新存储新的信息，从真正意义上完成群体的进化. 式(24)和式(25)是极小值优化问题的情形，而极大值优化问题可以很容易地转换为极小值优化问题：
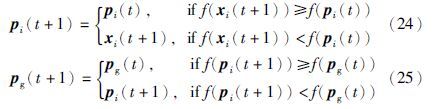
将粒子群算法的全局寻优能力和辅助变量法的抗噪声特性相结合，便可以对噪声环境下的分数阶系统进行很好的辨识. 两种算法的结合点在于，粒子群算法的每个粒子的适应值信息由辅助变量法计算得到，而辅助变量法进行参数估计需要的阶次信息，则由粒子的位置提供，即所有阶次的可能取值构成了粒子群算法的寻优空间. 整个辨识算法的详细步骤如下：
(1) 初始化粒子种群的参数： 种群大小M、 维数D、 粒子搜索空间的范围[xmin，xmax]、 粒子速度限值[vmin，vmax]； 同时初始化以下参数： 群体最大迭代次数tmax、 学习因子c1和c2、 惯性权重的范围[wmin，wmax].
(2) 初始化种群并计算每个粒子xi(i=1，2，…，M)的目标函数值f(xi)：
xi做为分数阶系统的阶次参数，即令q=xi，此时系统的待辨识参数为分子分母的系数θ，利用递推辅助变量法得到，由此可以得到辨识出的系统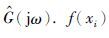
可由式(26)计算得到：
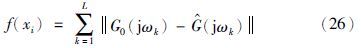
(3) 分别按照式(21)和式(22)更新每个粒子的速度和位置，并对速度和位置进行越界限制.
(4) 计算每个粒子的适应值； 分别按照式(24)和式(25)更新每个粒子的个体极值和全局极值.
(5) 若达到最大迭代次数，结束； 否则，返回步骤(3).
3.3 仿真实例本节同样基于式(20)所示的系统进行仿真实验，系统的同元次分数阶阶次q设定为未知的. 加入到系统原始数据上的随机噪声是均值为零的复随机噪声. 在不同的噪声下，辨识得到的结果也为随机变量，为了使结果具有统计意义，本文基于100组不同的观测数据进行辨识，记录100次辨识结果的均值. 同时，将粒子群算法和递推最小二乘算法相结合，基于同样的数据进行辨识. 另外，单独使用粒子群算法也可以对分数阶系统参数进行辨识[21]，为了便于比较，本文也采用了单独使用粒子群算法的方法辨识系统. 3种辨识方法的辨识结果列于表 1. 表 1中的“PSO_RIV”表示粒子群优化算法(particle swarm optimization，PSO)与递推辅助变量法(recursive instrumental variables，RIV)结合的辨识方法，“PSO_RLS”表示粒子群优化算法(PSO)与递推最小二乘法(recursive least squares，RLS)相结合的辨识方法，“PSO”则表示单独使用粒子群算法进行辨识的方法. 为了比较噪声对不同方法辨识精度的影响，分别对SNR为40和20的情况进行仿真实验.
| 待辨识参数 | q | a1 | a0 | b1 | b0 | |
| 真实值 | 0.8 | 5 | 10 | 2 | 3 | |
| SNR 40 | PSO_RIV | 0.800 | 5.000 | 10.000 | 2.000 | 3.000 |
| PSO_RLS | 0.800 | 4.979 | 10.006 | 1.996 | 3.000 | |
| PSO | 0.814 | 5.403 | 10.146 | 2.121 | 3.050 | |
| SNR 20 | PSO_RIV | 0.800 | 5.002 | 10.049 | 2.001 | 3.016 |
| PSO_RLS | 0.431 | -1.301 | 4.882 | 0.150 | 1.292 | |
| PSO | 0.822 | 5.581 | 10.183 | 2.174 | 3.061 | |
值得注意的是，以上3种方法的实验编程中，粒子群算法均为主程序，不同的是粒子的目标函数值的计算方法. 这就造成了不同的方法具有不同的时间复杂度. 在本文的实验中，算法运行的环境如下： 操作系统为Windows XP，CPU为Pentium Dual-Core E5200，2.50 GHz，内存为3.00 GB，仿真平台为Matlab 7.1版本. PSO_RIV和PSO_RLS中粒子种群大小为50，种群进化最大迭代次数为100，数据长度L为1 000，两种算法运行一次辨识程序所用的时间分别为325 s和301 s. 而PSO方法在相同的设置下运行一次辨识程序所用的时间为24 s. 因此，当设置PSO方法的参数时，将种群最大迭代次数增加为1 400，此时，运行一次辨识程序的时间为327 s.
由运算结果可知，PSO_RLS方法在噪声较小时是可行的，但在噪声较大时有很大的误差. 而PSO_RIV在噪声较大的环境下仍能取得很好的辨识结果. 在单独使用PSO方法时，尽管迭代次数增加为前面两种方法的14倍，而当运算时间基本相同时，但在噪声较小和较大的两种情况下，PSO方法的辨识精度都要低于PSO_RIV. 另外，本文在实验中同样应用了改进的粒子群算法单独对系统进行辨识，如CLPSO[22](comprehensive learning PSO)，ALC-PSO[23](PSO with an aging leader and challengers)，其辨识精度虽然在PSO方法的基础上有所提高，但都要低于PSO_RIV方法.
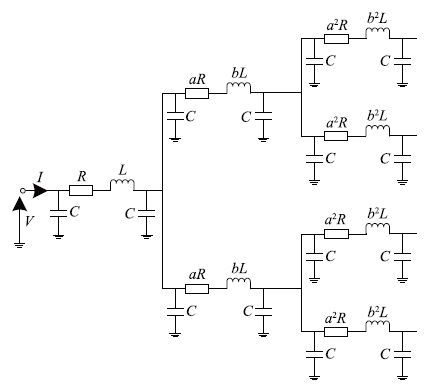
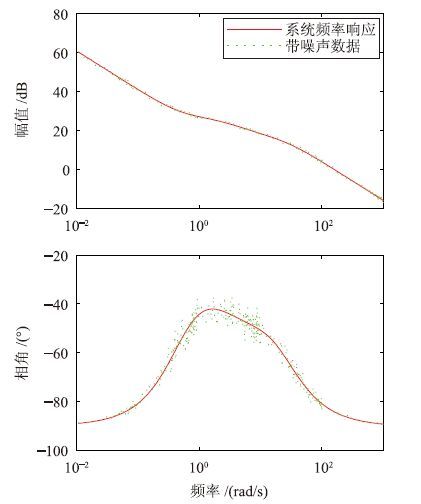
4 电网络系统的分数阶辨识以上讨论的为同元次分数阶系统的辨识方法，下面通过一个电网络系统的辨识实例将其扩展到更一般的分数阶系统的辨识上. 待辨识电网络系统如图 3所示，其中，R=100 Ω，L=0.001 H，C=0.001 F，系数a=3，b=a2. 在[0.01，1 000]的频率范围内按对数均匀取500个频率点，每个频率点下电网络阻抗的频率特性可以通过实验的方法获得. 在原始频率响应的实部数据和虚部数据分别加入了均值为零的噪声，信噪比SNR均为20，由加入噪声的实部数据和虚部数据可得到混有噪音的幅频特性和相频特性. 原系数的实际频域响应数据和混有噪声的数据如图 4所示. 本文的目的是通过混有噪声的数据辨识出电网络阻抗的模型.
|
| 图 3 电网络结构示意图 Fig. 3 Structural diagram of electric network |
|
| 图 4 电网络频率响应数据 Fig. 4 Frequency response data of electric network |
为了尽可能获得更加精确的模型，这里采用的模型类不局限于同元次分数阶系统，而是扩展到一般分数阶系统. 首先根据电网络阻抗的频率响应确定分数阶模型的结构[24]如式(27)所示：
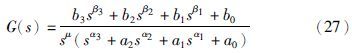
所示的系统为带有积分环节的一般分数阶系统，当利用递推辅助变量法得到多项式系数的参数估计值时，观测向量zk、 hk和辅助向量hk*中都需要用到阶次的信息，将其中的nq，(n-1)q，…，q替换成相应的阶次αn，αn-1，…，α1，将mq，(m-1)q，…，q替换为相应的阶次βm，βm-1，…，β1，同时加入积分环节的影响，可得zk、 hk和hk*分别如式(28)、 (29)和式(30)所示：
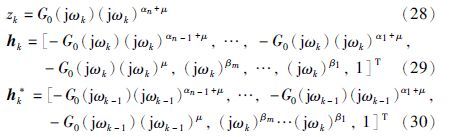
在得到观测向量和辅助变量的新表达式后，按照3.2节的辨识方法，可以得到待辨识电网络的分数阶模型表达式，如式(31)所示：
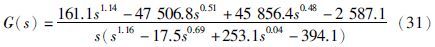
图 5中绘制了式(31)所示系统的频率响应，同时给出了整数阶系统的递推辅助变量法的辨识结果，整数阶模型如式(32)所示：
|
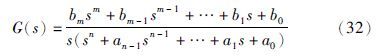
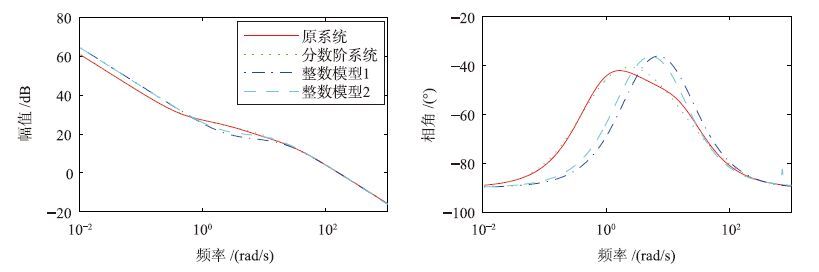
| 图 5 辨识结果 Fig. 5 Identification results |
由系统的频率特性可得m=n. 图 5中同时给出了n=2和n=3的辨识结果，分别为整数模型1和整数模型2. 从图 5可以看到，在有噪声的环境下，本文的方法仍然可以很好地辨识出系统. 由于实际的电感和电容在本质上是分数阶的，因此用分数阶模型来描述电网络阻抗比用整数阶模型要更加精确.
5 结论采用分数阶模型描述一些复杂的实际系统比整数阶模型更加精确简洁. 分数阶建模方法也受到越来越多的关注. 本文首先推导了分数阶系统在频域内的递推辅助变量辨识方法，在已知分数阶阶次的前提下，能够很好地对噪声环境中的系统进行辨识. 接着，将递推辅助变量法与粒子群算法相结合，得到的辨识方法能够在分数阶阶次未知的情况下对系统进行整体辨识. 电网络系统的辨识实例将辨识算法扩展到一般分数阶系统上，在展示本文方法的有效性的同时，也展示了分数阶模型在描述本质上是分数阶的实际系统时的优势. 本文提出的辨识方法中，还有一些问题值得去思考，如新的辅助变量的构造方法，粒子群优化算法中目标函数的选取等，以进一步提高辨识的精度.
| [1] | 宋勇军, 雷胜友, 韩铁林. 一种新的岩石非线性黏弹塑性流变模型[J]. 岩石力学, 2012, 33(7): 2076-2080. Song Y J, Lei S Y, Han T L. A new nonlinear viscoelasto-plastic rheological model for rocks[J]. Rock and Soil Mechanics, 2012, 33(7): 2076-2080. |
| [2] | 陈亮, 陈寿根, 张恒, 等. 基于分数阶微积分的非线性黏弹塑性蠕变模型[J]. 四川大学学报: 工程科学版, 2013, 45(3): 7-11. Chen L, Chen S G, Zhang H, et al. A nonlinear viscoelasto-plastic creep model based on fractional calculus[J]. Journal of Sichuan University: Engineering Science Edition, 2013, 45(3): 7-11. |
| [3] | Beaulieu A, Bosse D, Micheau P, et al. Measurement of fractional order model parameters of respiratory mechanical impedance in total liquid ventilation[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(2): 323-331. |
| [4] | Galvao R K H, Hadjiloucas S, Kienitz K H, et al. Fractional order modeling of large three-dimensional RC networks[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(3): 624-637. |
| [5] | 李明震, 董金钟. 基于分数阶Maxwell模型的振荡流传热特性分析[J]. 北京航空航天大学学报, 2012, 38(11): 1562-1566. Li M Z, Dong J Z. Theoretical analysis of heat transfer in oscillating flows with fractional Maxwell model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(11): 1562-1566. |
| [6] | 范文萍, 蒋晓芸. 带有分数阶热流条件的时间分数阶热波方程及其参数估计问题[J]. 物理学报, 2014, 63(14): 1-6. Fan W P, Jiang X Y. Parameters estimation for a one-dimensional time fractional thermal wave equation with fractional heat flux conditions[J]. Acta Physica Sinica, 2014, 63(14): 1-6. |
| [7] | 廖增, 彭程, 王永, 等. 分数阶系统时域子空间辨识[J]. 信息与控制, 2011, 40(5): 658-663, 668. Liao Z, Peng C, Wang Y, et al. Time domain subspace method for fractional order system identification[J]. Information and Control, 2011, 40(5): 658-663, 668. |
| [8] | Djamah T, Mansouri R, Djennoune S, et al. Optimal low order model identification of fractional dynamic systems[J]. Applied Mathematics and Computation, 2008, 206(2): 543-554. |
| [9] | 朱呈祥, 邹云. 基于信息压缩矩阵交替变换的分数阶系统结构、阶次与参数的同时辨识方法[J]. 自动化学报, 2012, 38(8): 1280-1287. Zhu C X, Zou Y. Simultaneous identification of fractional-order system structure and order and parameters based on alternately transforming condensed information matrix[J]. Acta Automatica Sinica, 2012, 38(8): 1280-1287. |
| [10] | 李远禄, 于盛林. 非整数阶系统的频域辨识法[J]. 自动化学报, 2007, 33(8): 882-884. Li Y L, Yu S L. Identification of non-integer order systems in frequency domain[J]. Acta Automatica Sinica, 2007, 33(8): 882-884. |
| [11] | 李远禄, 于盛林, 郑罡. 非整数阶系统频域辨识的递推最小二乘算法[J]. 信息与控制, 2007, 36(2): 171-175. Li Y L, Yu S L, Zheng G. A recursive least squares algorithm for frequency domain identification of non-integer order systems [J]. Information and Control, 2007, 36(2): 171-175. |
| [12] | 李大字, 范伟光, 高彦辰, 等. 分数阶系统的迭代最小二乘辨识算法[J]. 江南大学学报: 自然科学版, 2010, 9(4): 404-408. Li D Z, Fan W G, Gao Y C, et al. Iterative least square identification algorithm for fractional order system [J]. Journal of Jiangnan University: Natural Science Edition, 2010, 9(4): 404-408. |
| [13] | 彭程, 王永. 分数阶系统的一种频域辨识算法[J]. 东南大学学报: 自然科学版, 2008, 38(增刊Ⅱ): 23-26. Peng C, Wang Y. Frequency domain identification algorithm for fractional order systems[J]. Journal of Southeast University: Natural Science Edition, 2008, 38(Sup.Ⅱ): 23-26. |
| [14] | Mansouri R, Bettayeb M, Djamah T, et al. Vector fitting fractional system identification using particle swarm optimization[J]. Applied Mathematics and Computation, 2008, 206(2): 510-520. |
| [15] | 李旺, 张国庆, 王永. 分数阶系统频域辨识算法[J]. 控制理论与应用, 2010, 27(8): 1118-1122. Li W, Zhang G Q, Wang Y. Frequency domain identification of fractional order systems[J]. Journal of Control Theory & Applications, 2010, 27(8): 1118-1122. |
| [16] | Pintelon R, Schoukens J. System identification: A frequency domain approach[M]. 2nd ed. Piscataway, NJ, USA: IEEE, 2012: 1-28, 323. |
| [17] | Akcay H. An insight into instrumental variable frequency-domain subspace identification[J]. Automatica, 2010, 46(2): 375-382. |
| [18] | Van Herpen R, Oomen T, Steinbuch M. Optimally conditioned instrumental variable approach for frequency-domain system identification[J]. Automatica, 2014, 50(9): 2281-2293. |
| [19] | Gilson M, Welsh J S, Garnier H. Frequency-domain instrumental variable based method for wide band system identification[C]//2013 American Control Conference. Piscataway, NJ, USA: IEEE, 2013: 1663-1668. |
| [20] | 林军, Poinot T, 李寿涛, 等. 非整数阶系统的频率辨识[J]. 控制理论与应用, 2008, 25(3): 517-520. Lin J, Poinot T, Li S T, et al. Identification of non-integer-order systems in frequency domain[J]. Journal of Control Theory & Applications, 2008, 25(3): 517-520. |
| [21] | 张永宏, 王琦, 李远禄, 等. 多质量弹性扭转系统的模型辨识[J]. 信息与控制, 2015, 44(1): 62-66. Zhang Y H, Wang Q, Li Y L, et al. The model identification of the multi-mass elastic torsion system[J]. Information and Control, 2015, 44(1): 62-66. |
| [22] | Liang J J, Qin A K, Suganthan P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions [J]. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295. |
| [23] | Chen W N, Zhang J, Lin Y, et al. Particle swarm optimization with an aging leader and challengers[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(2): 241-258. |
| [24] | 汪纪锋. 分数阶系统控制性能分析[M]. 北京: 电子工业出版社, 2010: 42-54. Wang J F. Control performance analysis for fractional order systems[M]. Beijing, Publishing House of Electronics Industry, 2010: 42-54. |