2. 哈尔滨工业大学控制理论与制导技术研究中心, 哈尔滨 黑龙江 150001
2. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China
1 引言
矩阵二阶控制系统在实际工程中得到了广泛的应用. 远洋轮船能够对操作员的操纵做出快速准确的响应; 现代汽车采用悬挂控制系统、 防滑操纵控制系统和引擎控制系统等使得在行驶过程中具有较好的平稳性; 机械臂以0.1英寸或者更高的精确度将数百磅的物件放置在指定位置. 工业自动化控制生产中使用铸造、 切割或焊接设备能够使加工更安全、 更高效和更精密.
上述许多系统可以被描述成如下的一类二阶动力学系统
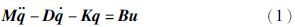
本文的研究主要受到Ouyang、 Zhang等人近年来发表文[10, 11]的启发,他们利用位置—加速度反馈研究无阻尼振动系统部分特征结构配置问题. 众所周知,加速度可以通过加速度计测量得到,所以利用加速度传感器测量结构的动态响应比利用速度或位置传感器更加有利与可靠. 目前,研究人员已经确认使用位置—加速度反馈在不同工程领域中的重要性[12, 13, 14, 15]. 文[16]提出引用加速度反馈可以有效提高船舶动力系统的定位精度,建立了一种新的方法用来补偿波浪漂移产生的变化力; 文[17]首先分析了影响机器人位置控制性能的几个因素,然后针对这些不利因素提出了一种基于加速度传感器的控制方法; 文[18]分析了加速度控制器对时滞系统的影响,结果表明应用加速度传感器具有较好的鲁棒性和控制效果.
本文不同于文[19, 20]中提出的将位置—加速度反馈算法直接作用于二阶系统模型,而是将二阶形式的系统转化为一阶形式,这是由于一阶模型的基本特性近似于二阶模型,且二阶系统的计算较为困难,在工程设计的许多问题中过分讲究其精度往往是不必要的. 所以二阶线性系统(1)的控制特性可以通过研究其相应的一阶状态空间模型来实现.
令


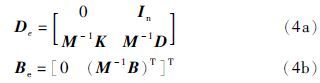
本文的主要特点是利用位置和加速度变量,建立了反馈增益控制器和特征向量矩阵的参数化表达式,解决了矩阵二阶线性系统的特征结构配置问题. 提出的充要条件保证了该问题的可解性,且通过位置—加速度反馈为系统提供了有效的自由度. 最后,数值算例表明了该算法的有效性.
2 问题的描述为了保证二阶动力学系统(1)的可解性,本文提出如下假设:
假设1 rank[M]=n; rank[B]=r.
假设2 rank[Ms2-Ds-K B]=n, s∈C.
s∈C.
注1 一阶状态空间模型(3)是可控的,那么二阶线性系统(1)也是可控. 假设2给出了可控条件,通过PBH(Popov-Belevitch-Hautus)判据的推广很容易获得结论.
证明 假设2等价于以下方程:
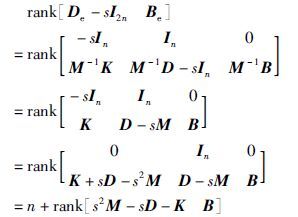
通过对PBH判据的延伸应用,很容易获得系统(1)可控的结论. 基于以上假设的成立,构造位置—加速度反馈控制律:

将位置—加速度反馈控制律应用到系统(1)中,得到如下方程
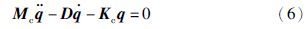
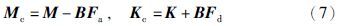
为了便于计算,将上述系统(6)等价于如下一阶状态空间模型

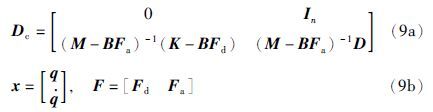
注2 矩阵Dc为非退化阵,原因是非退化矩阵具有如下对角形式的Jordan标准型
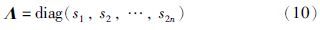
通过一阶模型研究其二阶模型的系统属性,可使特征结构配置问题的处理变得简单与方便,并且根据矩阵的性质,非退化矩阵具有良好的特性,即非退化矩阵的特征值具有较小的灵敏度. 这为不确定性因素存在的情况下的控制系统设计提供了有利条件.
综上所述,问题的求解转化为求取反馈增益矩阵F的参数化表达式,进一步推导出满足位置—加速度反馈形式的控制律.
引理1 令Dc与Λ分别由式(9a)和式(10)给出,存在满秩矩阵Vi∈Cn×2n,i=0,1,使得下式成立
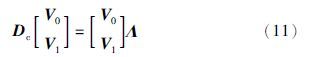
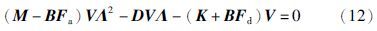
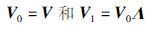
证明 因为
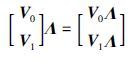
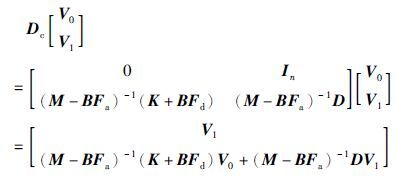
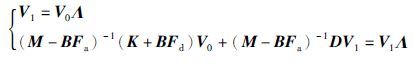
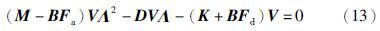
根据引理1可知,当且仅当存在一个矩阵V∈Cn×2n满足式(13)时,矩阵Dc具有对角形式的Jordan标准型,且矩阵Dc相应的特征向量矩阵可表示为下列形式

为了求解反馈增益矩阵F的参数化表达式,关键的步骤就是解决以下ESA(EignStructure Assignment)问题.
3 问题ESA的求解已知反馈增益矩阵F和特征向量矩阵V∈Cn×2n,令
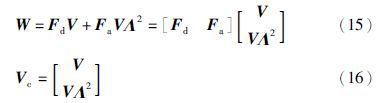
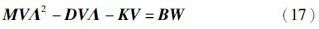
不难看出,方程(17)为一类广义Sylvester矩阵方程,在特征结构配置、 观测器设计等控制系统设计方面有着许多应用. 这里将在假设矩阵Vc可逆的条件下,给出方程(17)的完全解析通解. 式(15)等价于如下矩阵方程形式:
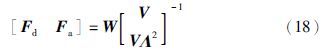
为了对应反馈增益矩阵F的结构,赋予矩阵V、 W一种相应的结构形式,将其按列分块为
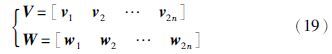
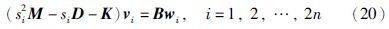
因假设2的成立,则存在两个单模矩阵P(s),Q(s)使得下式成立
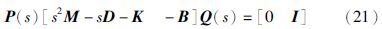
利用对矩阵[s2M-sD-K -B]进行初等变换求得单模阵P(s)、 Q(s),然后将单模阵Q(s)做如下分块
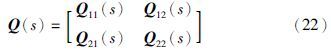
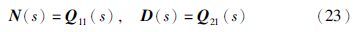
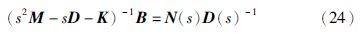
利用上述右互质分解式推导出定理1来得到方程(17)的完全解析解.
定理1 在假设2成立的条件下,矩阵多项式N(s),D(s)为满足右互质分解式(24)决定的实系数多项式,则
(1) 问题ESA有解的充要条件就是存在一组参数向量fi∈Cr,i=1,2,…,2n满足下面两个约束条件
约束C1: 当si=sj成立时,有fi=fj.
约束C2: det Vc≠0
其中
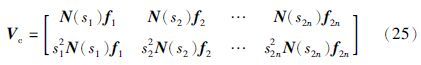
(2) 当上述约束条件得到满足时,问题ESA的所有解可由下式给出
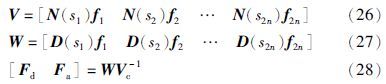
证明 右互质分解方程(24)可写成如下形式:
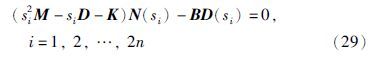
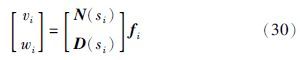
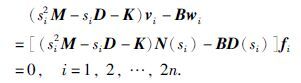
由此,对任意的参数向量fi∈Cr,i=1,2,…,2n及N(s)和D(s)可以得到矩阵Vc和W,利用式(18)容易得出位置—加速度反馈控制律Fd和Fa,证毕.
综上分析,结合上述定理给出如下矩阵二阶系统特征结构配置的算法:
算法ESA
第一步: 求解出满足式(21)的单模阵P(s)和Q(s),并对单模阵Q(s)进行分块,求解出两个右多项式矩阵N(s),D(s)使其满足式(24).
第二步: 给出参数向量fi∈Cr,i=1,2,…,2n,使其同时满足约束C1与C2,通过式(25)~(27)计算出矩阵Vc以及W的参数化表达式.
第三步: 利用第二步给出的矩阵Vc以及W的参数化表达式,结合式(28)计算得到反馈增益矩阵Fd,Fa.
4 数值算例考虑如图 1所示的三自由度机械系统,该系统的动力学模型如下式所示
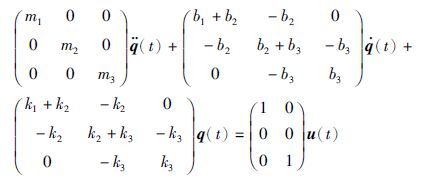
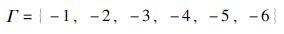

|
| 图 1 三质量—弹簧—阻尼器系统 Fig. 1 Three mass-spring-dashpots system |
由此可以得到二阶动力学系统的系数矩阵
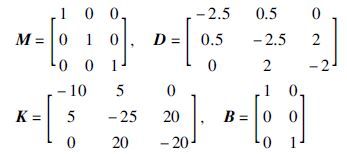
通过式(24)得到右互质多项式矩阵N(s)和D(s)
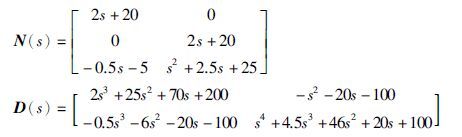
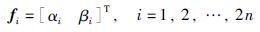
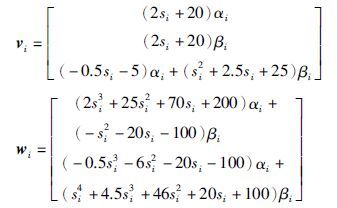
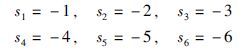
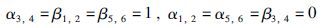
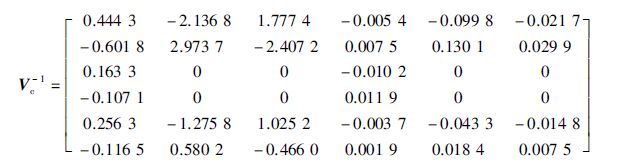
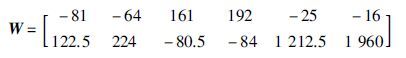

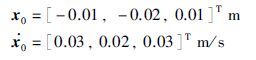

|
| 图 2 实例仿真的系统响应 Fig. 2 System′s response for the simulation example |
在线性系统中,特征结构配置不仅需要配置目标特征值,同时也需要配置所期望的闭环特征向量. 由于在控制系统设计中,特征结构配置设计与极点配置设计相比较,能够更好地把握系统特性,因此对特征结构配置问题的研究是十分必要的. 基于位置—加速度反馈的二阶系统特征结构配置问题的研究,由于很多系统例如机器人机械手与环境接触模型、 变阻尼减震控制系统等,都可以简化为质量弹簧系统,而本文方法主要是基于解决质量—弹簧—阻
尼系统的特征结构配置问题,由此可推广至一般的二阶动力学系统.
本文解决了基于位置—加速度反馈的二阶系统特征结构配置问题,提出了一种简单、 有效的参数化方法,利用加速度反馈的优越性,提高了求解精度,并结合右互质分解,允许闭环系统特征值是未知的. 通过对问题的求解获得闭环特征向量矩阵及反馈控制律的完全参数表达式. 表达式中包含了系统设计中的全部自由度,并通过选取适当的设计参数来满足一个系统所期望的设计要求. 在相同控制系统中,可利用该方法进行鲁棒设计,利用提供的自由度来满足系统性能指标. 本文涉及的参数化方法直接将二阶系统模型转化为一阶形式,为系统设计提供了方便,算法简单,无“返回”步骤.
| [1] | 顾大可, 段广仁. 矩阵二阶线性系统的鲁棒渐近跟踪[J]. 信息与控制, 2013, 42(2): 181-188. Gu D K, Duan G R. Robust asymptotic tracking in matrix second-order linear system[J]. Information and Control, 2013, 42(2): 181-188. |
| [2] | 黄玲, 尤波, 段广仁, 等. 二阶动力学系统的输出反馈模型跟踪[J]. 哈尔滨理工大学学报, 2010, 15(4): 98-101. Huang L, You B, Duan G R, et al. Model tracking control in second-order dynamical system by output feedback[J]. Journal of Harbin University of Science and Technology, 2010, 15(4): 98-101. |
| [3] | 张晓艳, 孙建桥, 丁千. 时滞动力学系统的L-K稳定性条件分析[J]. 西安交通大学学报, 2013, 47(5): 72-76. Zhang X Y, Sun J Q, Ding Q. Analysis of Lyapunov-Krasovskii stability for dynamical system with time delay[J]. Journal of Xi'an Jiaotong University, 2013, 47(5): 72-76. |
| [4] | 徐文建. 二阶系统的数字PID校正虚拟仪器的设计与实现[D]. 天津: 天津大学, 2007. Xu W J. Design and implementation of virtual instrument of digital PID emendation for second-order control system[D]. Tianjin: Tianjin University. |
| [5] | Hassan M M, Amin M H. Recursive eigenstructure assignment in linear systems[J]. International Journal of Control, 1987, 45(1): 291-310. |
| [6] | Duan G R, Patton R J. Robust pole assignment in descriptor systems via proportional plus partial derivative state feedback[J]. International Journal of Control, 1999, 72(13): 1193-1203. |
| [7] | Rabindra N D, Partha P, Sung H P. Modified robust second-order slope-rotatable designs[J]. Communications in Statistics-Theory and Methods, 2015, 44(1): 80-94. |
| [8] | Namavar M, Fleming A J, Aleyaasin M, et al. An analytical approach to integral resonant control of second-order systems[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(2): 651-659. |
| [9] | 王国胜, 易良海, 吕强. 二阶动力学系统部分特征结构配置设计的完全参数化方法[J]. 黑龙江大学自然科学学报, 2005, 22(6): 737-742. Wang G S, Yi L H, Lü Q. Design of eigenstructure assignment in a class of sencond-order dynamic systems: A complete parametric method[J]. Journal of Natural Science of Heilongjiang University, 2005, 22(6): 737-742. |
| [10] | Zhang J F, Ouyang H J, Zhang Y G, et al. Partial quadratic eigenvalue assignment in vibrating systems using acceleration and velocity feedback[J]. Inverse Problems in Science and Engineering, 2015, 23(3): 479-497. |
| [11] | Zhang J F, Ouyang H J, Yang J. Partial eigenstructure assignment for undamped vibration systems using acceleration and displacement feedback[J]. Journal of Sound and Vibration, 2014, 333(1): 1-12. |
| [12] | 潘颖, 刘小妹, 范志毅. 基于静态加速度反馈不确定结构系统H∞鲁棒控制[J]. 上海工程技术大学学报, 2006, 20(3): 230-234. Pan Y, Liu X M, Fan Z Y. Control method based on static acceleration feedback to uncertain structure[J]. Journal of Shanghai University of Engineering Science, 2006, 20(3): 230-234. |
| [13] | Alujević N, Tomac I, Gardonio P. Tuneable vibration absorber using acceleration and displacement feedback[J]. Journal of Sound and Vibration, 2012, 331(12): 2713-2728. |
| [14] | An F, Chen W D, Shao M Q. Study on discrete acceleration feedback control with time delay[J]. Journal of Vibration and Control, 2015, 21(7): 1267-1285. |
| [15] | Shang W W, Cong S. Motion control of parallel manipulators using acceleration feedback[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 314-321. |
| [16] | 李晨曦, 俞孟蕻, 杨金节. 应用加速度反馈的船舶动力定位系统研究[J]. 科学技术与工程, 2014, 14(8): 269-273. Li C X, Yu M H, Yang J J. The study of applying acceleration feedback for ship dynamic positioning system[J]. Science Technology and Engineering, 2014, 14(8): 269-273. |
| [17] | 谈大龙, 宋亦旭, 韩建达. 基于车体加速度反馈的轮式移动机器人轨迹跟踪控制研究[J]. 机器人, 2002, 24(4): 289-293. Tan D L, Song Y X, Han J D. Trajectory tracking control for a wheeled mobile robot based on vehicle acceleration feedback[J]. Robot, 2002, 24(4): 289-293. |
| [18] | 安方, 陈卫东. 时滞加速度反馈的振动主动控制方法研究[J]. 振动工程学报, 2012, 25(4): 401-410. An F, Chen W D. Active vibration control using time-delayed acceleration feedback[J]. Journal of Vibration Engineering, 2012, 25(4): 401-410. |
| [19] | Abdelaziz T H S. Robust pole placement for second-order linear systems using velocity-plus-acceleration feedback[J]. IET Control Theory & Applications, 2013, 7(14): 1843-1856. |
| [20] | Abdelaziz T H S. Eigenstructure assignment for second-order systems using velocity-plus-acceleration feedback[J]. Structural Control and Health Monitoring, 2013, 20(4): 465-482. |



