2. 东北石油大学计算机与信息技术学院, 黑龙江 大庆 163318
2. School of Computer and Information Technology, Northeast Petroleum University, Daqing 163318, China
1 引言
混合蛙跳算法(shuffled frog leaping algorithm,SFLA)[1]具有便于实现、 计算速度快和全局寻优能力强的优势,在很多领域得到了广泛应用. Elbeltagi等[2]证明了采用SFLA解决某些连续优化问题的成功率和收敛速度都优于遗传算法,近似于粒子群算法. Amiri等[3]用SFLA对K均值方法进行改进,实验结果表明新算法的求解质量和运行速度优于基于蚁群等算法的聚类算法. 但SFLA也存在早熟、 收敛速度慢且求解精度不高的缺点,使其在求解高维连续优化问题的效果不够理想. 导致该缺陷的主要原因是在进化后期种群多样性迅速下降,缺乏局部细化搜索能力. 为了提高蛙跳算法的寻优性能,许多学者[4, 5, 6, 7, 8, 9, 10]在算法的参数调整、 子群更新方式和与智能算法相结合等方面进行了改进,取得了很好的优化效果.
大部分进化算法的产生都来源于对生物进化机理的模拟,多数学者的研究也多关注生物自然选择进化方面. 文[11]指出文化能使种群以一定的速度进化和适应环境,而这个速度是超越单纯依靠基因遗传生物进化速度. 文化作为信息存储的载体在社会群体之间和群体内部广泛地传递,并能被社会所有成员继承,从而有效地指导成员的行为来解决问题. 文[12]提出一种文化蛙跳算法,有效地改进了经典算法的性能,但算法进化过程中需要确定概率门限. 本文提出一种自适应混合文化蛙跳算法(adaptive mixed culture shuffled frog leaping algorithm,AMC-SFLA),用改进的蛙跳算法来进化群体空间,用云模型和反向算法作为信念空间的进化方式,完成知识经验的形成、 存储和传播,利用反向混沌模型进化外部空间增加种群多样性,三者既相互独立又相互联系.
2 自适应混合文化蛙跳算法原理 2.1 群体空间的进化方式群体空间的进化操作采用蛙跳算法来完成,但其进化机理使其在求解高维连续优化问题时效果不够理想,其中主要原因是当最差解更新时,先参考子群内最优个体进行进化. 若进化后的个体适应度没有提高,则再参考全局最优个体进行个体进化. 这种方式使得获取的信息过于单一,没有同时考虑这两个最优个体对最差个体的影响,导致算法在处理大规模复杂问题时容易陷入局部最优. 因此,本文提出以下改进方法: 依据最优觅食理论,动物觅食行为中总是趋向于耗费更低的能量而获得更多的食物,以达到能效最好[13, 14]. 计算某一个体受到能效吸引力的公式如下:
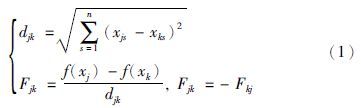
这里仅考虑Fjk≥0的情况,设对更新个体产生最大能效作用力的个体所处的位置为xnx,为了丰富进化个体的参考信息,更新个体位置时同时参考子群内最优个体xb、 全局最优个体xg和xnx. 个体更新公式如下:
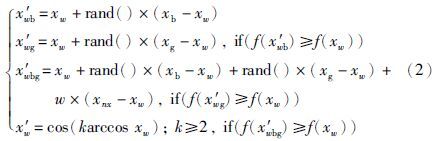
信念空间的个体来自于群体空间的最优子集. 社会学原理指出优秀个体附近往往存在着更优个体,即局部最优值附近往往存在更优值,在其附近更有机会发现最优值. 故为了能让信念空间更好指导群体空间,需要在信念空间中发掘更多的优秀个体,云模型是一种定性概念与定量数值转换的不确定转换模型,具有不确定性中伴有确定性、 稳定中存在变化的特点,能表征自然界中物种进化的基本原理[15, 16, 17],采用期望Ex、 熵En和超熵He来表示. Ex表示最能代表定性概念的值,是新个体产生的中心,故将空间内的每个个体作为Ex; En表示定性概念的不确定性程度,反应随机性与模糊性之间的关联,体现优化空间中解的搜索范围,故将当代适应度方差σ2作为En动态改变搜索范围; He是熵的度量,反映在论域空间代表该语言值的所有点的不确定度的凝聚性,它由熵的随机性和模糊性共同决定,将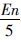 作为He,初期加大算法的随机性,后期加强算法的稳定性. 为扩大解空间的搜索范围,将信念空间的个体及其反向个体都看作一个正态云滴C(Ex,En,He),用它们分别产生与空间数量相同的一组云滴,如果新解优于原来个体则用其替换,实现方法如下:
作为He,初期加大算法的随机性,后期加强算法的稳定性. 为扩大解空间的搜索范围,将信念空间的个体及其反向个体都看作一个正态云滴C(Ex,En,He),用它们分别产生与空间数量相同的一组云滴,如果新解优于原来个体则用其替换,实现方法如下:
Step 1: 按公式x′=a+b-x求解个体的反向解,a、 b为解区间,然后分别对x和x′按照下面方法求解云滴;
Step 2: 产生一个以En为期望值,He为标准差的正态随机数En′;
Step 3: 产生一个以Ex为期望值,En′的绝对值为标准差的正态随机数X;
Step 4: 计算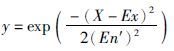 ,令y为定性概念C的确定度;
,令y为定性概念C的确定度;
Step 5: 重复Step 2~Step 5直到产生n个云滴为止.
2.3 外部空间的进化方式自然界和人类社会活动不仅有渐变和连续光滑变化的现象,还存在突变和跃迁的现象,从某种意义上来讲突变有利于新物种的产生. 虽然文化算法的信念空间通过知识来指导群体空间进化,对于某些特殊问题,来自于外部的知识对文化算法的进化过程起到了至关重要的作用[18]. SFLA在分组过程中适应值相对较差的个体总是被分在最后一组,使得该组最差个体向本组最优个体学习所获得的效果不如前面的分组,所以可以将最后分组的个体作为外部知识来指导进化,但须改变原有的进化方式. Tizhoosh[19]于2005年提出一种反向学习机制的机器学习方法,Rahnamayan证明反向学习算法具有较快的学习速度和更强的优化能力[20]. 混沌理论看似混乱却有着精致的内在结构,具有随机性、 遍历性及规律性等特点[21, 22]. 应用k阶Chebyshev混沌映射对个体进行映射,文[22]证明k为偶数时产生序列的随机性好,且2阶Chebyshev混沌映射和μ=4时的Logistic强混沌映射的相图一致,产生的个体新位置呈现遍历性、 随机性和多样性,可有效地在收敛区域以外空间搜索全局最优位置,外部空间的进化方式如下:
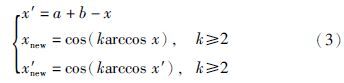
利用接受函数将群体空间的一组最优子集传递给信念空间. 在最优化问题中,一般是按一定的比例选取适应度最优的个体. 由于经典蛙跳算法各子群每一次迭代都会对个体适应度进行排序,所以对于每一个子群设置一个选择比例α,按这个比例取每个子群中前几个最优个体来传递个体经验,由各个子群提供的优秀个体和信念空间的个体采取锦标赛法来更新信念空间的个体. 考虑到不同迭代次数中每个蛙群子群的个体对信念空间的贡献不一定都是一致的,所以每个分组选取的比例也应该不同,适应度好和子群多样性好的分组应该比例高一些. 设蛙跳算法共分为N组子群,令X(t)=(x1(t),x2(t),…,xN(t))是第t代每个分组的最优位置,以求最小值为例,fbest(X(t))=min{f(xi(t))i=1,2,…,N}为当代N个分组中最好的适应值,fworst(X(t))=max{f(xi(t))i=1,2,…,N}为当代N个分组中最差的适应值,D(t)=(E1(t),E2(t),…,EN(t))为N个分组中适应度的方差,故计算每个分组的选择比例为
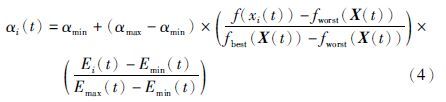
影响函数设计涉及到信任空间和外部空间的影响函数,在算法迭代初期应该多利用信念空间对群体空间的影响,减少外部空间的影响. 迭代后期为了避免陷入局部最优解,要增加外部空间对群体空间的干扰. 故分别设计信任空间和外部空间的影响函数并提供个体个数计算公式如下:
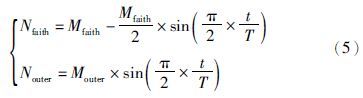
综上所述,本文提出的求解连续空间优化问题的自适应混合文化蛙跳算法流程如下:
(1) 初始化群体空间中蛙跳算法种群及其相关参数;
(2) 计算群体空间的适应度,根据接受函数生成信念空间中的个体,并将最后分组的个体赋值到外部空间;
(3) 按照蛙跳算法进化规则计算每个分组内个体适应值,符合结束条件则退出,否则执行(4);
(4) 按照改进的蛙跳算法独立进化群体空间,按照云模型算法及反向算法独立进化信念知识,按照Chebyshev混沌映射和反向算法独立进化外部知识;
(5) 若个体适应值满足结束条件则退出,否则执行(6);
(6) 将群体空间的个体按照接受函数规则更新信念空间中的知识和外部空间的知识;
(7) 信念空间和外部空间利用影响函数更新群体空间的个体;
(8) t=t+1;
(9) 转到(4),直到满足终止条件.
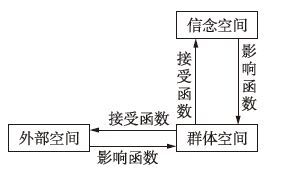
|
| 图 1 算法的基本框架 Fig. 1 The basic framework of the algorithm |
算法采用Java语言实现,运行平台为Windows 2003,处理器为双核2.5 GHz,内存为2 G. 以8个函数极值优化为例,并通过与粒子群算法(particle swarm optimization,PSO)、 经典蛙跳算法(shuffled frog leaping algorithm,SFLA)、 无外部空间混合文化蛙跳算法(no outer space mixed culture shuffled frog leaping algorithm,NOSMC-SFLA)、 固定比例混合文化蛙跳算法(fixed mixed culture shuffled frog leaping algorithm,FMC-SFLA)和自适应混合文化蛙跳算法(adaptive mixed culture shuffled frog leaping algorithm,AMC-SFLA)对比,验证算法的优化性能. 粒子群参数设置如下[23]: 惯性因子为0.729 8,自身因子为1.496 18,全局因子为1.496 18,种群大小均为200,最大迭代代数均为5 000,每个函数独立运行20次,误差精度为10-10. 蛙跳算法参数设置如下: Chebyshev混沌映射参数k设置为4,种群大小均为200,分为10个子群,每个子群20只青蛙,子群内部迭代次数为10次,最大迭代代数均为5 000,每个函数独立运行20次,为验证算法寻找最优解的求解精度,误差精度为10-10. 均匀设计[24]是一种实验设计方法,它舍弃了正交设计的整齐可比性,只考虑实验点的均匀分布,能用较少的实验点获得最好的均匀性,通过均匀设计设计FMC-SFLA的影响函数接受比例为0.25; 然后比较5种算法的最优结果、 最差结果、 平均结果、 平均时间、 平均进化代数、 成功率和方差. 本文所采用的实验仿真函数如下:
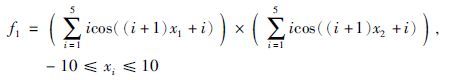
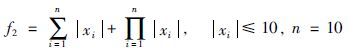
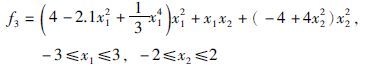
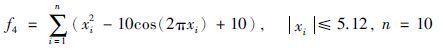

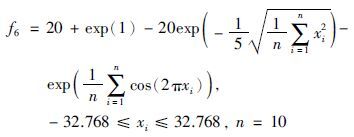
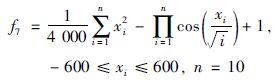
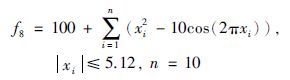
对比求解结果可知,本文所提的自适应混合文化蛙跳算法具有很好的求解精度和速度且在提高精度的同时能保持最优解的标准差较小,表现出了较好的稳定性. 由表 1到表 8的最优结果、 最差结果、 平均结果可知,AMC-SFLA寻优结果最好,NOSMC-SFLA和FMC-SFLA基本上能获得较好的寻优结果但求解精度不如AMC-SFLA. 主要因为采用反向学习机制和云模型算法的信念空间增加了个体接近最优解的机会且云模型的稳定倾向性可以较好地保护最优个体实现对周围更优个体的自适应定位,随机性可以保持个体多样性,加快算法的进化速度和寻优效率. 同时外部空间引入的混沌理论有利于在算法进化后期避免陷入局部最优,有利于获得全局最优解,进而克服算法在一些复杂函数时易早熟、 收敛速度慢、 容易陷入局部最优的缺点.
| 函数算法 | f1 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | -186.730 908 830 7 | -186.730 908 830 9 | -186.730 908 755 9 |
| SFLA | -186.730 908 830 9 | -186.730 908 830 9 | -186.730 908 836 2 |
| NOSMC-SFLA | -186.730 908 831 0 | -186.730 908 831 0 | -186.730 908 830 9 |
| FMC-SFLA | -186.730 908 831 0 | -186.730 908 831 0 | -186.730 908 830 9 |
| AMC-SFLA | -186.730 908 831 0 | -186.730 908 831 0 | -186.730 908 830 9 |
| 函数算法 | f2 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | 3.600 857 070 3E-4 | 0.634 130 242 2 | 0.272 766 764 2 |
| SFLA | -0.999 999 999 9 | 7.316 208 488 7 | 3.123 542 746 6 |
| NOSMC-SFLA | 2.892 469 321 5E-4 | 8.480 491 624 2E-3 | 7.201 330 445 4E-4 |
| FMC-SFLA | 5.098 692 124 4E-5 | 9.732 005 723 9E-5 | 7.579 033 653 9E-5 |
| AMC-SFLA | 2.892 469 321 5E-6 | 9.318 884 822 2E-6 | 7.219 068 626 5E-6 |
| 函数算法 | f3 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | -1.031 628 453 485 94 | -1.031 628 453 400 81 | -1.031 628 453 |
| SFLA | -1.031 628 453 484 61 | -1.031 628 453 391 5 | -1.031 628 453 435 906 1 |
| NOSMC-SFLA | -1.031 628 453 473 01 | -1.031 628 453 394 45 | -1.031 628 453 443 29 |
| FMC-SFLA | -1.031 628 453 477 71 | -1.031 628 453 393 01 | -1.031 628 453 297 088 7 |
| AMC-SFLA | -1.031 628 453 485 7 | -1.031 628 453 432 82 | -1.031 628 453 440 178 |
| 函数算法 | f4 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | 33.907 057 671 3 | 148.942 796 432 5 | 104.770 892 898 9 |
| SFLA | 2.098 913 785 8E-4 | 9.359 040 449 2E-2 | 5.252 850 394 6E-3 |
| NOSMC-SFLA | 4.183 437 429 8E-6 | 9.038 386 762 5E-6 | 6.507 423 239 1E-6 |
| FMC-SFLA | 2.675 347 740 6E-6 | 8.500 414 921 2E-6 | 5.862 741 955 7E-6 |
| AMC-SFLA | 8.992 457 338 7E-7 | 7.098 913 785 8E-6 | 3.427 926 603 4E-6 |
| 函数算法 | f5 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | 9.660 468 827 7E-11 | 0.013 900 757 8 | 9.81E-04 |
| SFLA | 1.088 032 456 9E-10 | 9.977 360 774 1E-10 | 7.727 605 530 0E-10 |
| NOSMC-SFLA | 6.354 694 421 0E-11 | 3.939 446 187 3E-10 | 7.797 032 368 2E-11 |
| FMC-SFLA | 2.381 828 233 1E-11 | 8.295 134 897 1-11 | 6.600 934 020 2E-11 |
| AMC-SFLA | 2.945 926 145 1E-12 | 6.354 694 421 0E-11 | 5.778 575 404 1E-11 |
| 函数算法 | f6 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | 8.245 496 116 9E-5 | 3.404 158 390 0 | 1.954 305 868 3 |
| SFLA | 1.840 812 703 9 | 1.840 812 703 9 | 1.840 812 703 9 |
| NOSMC-SFLA | 4.677 414 011 6E-6 | 8.895 195 691 1E-6 | 7.767 564 369 4E-6 |
| FMC-SFLA | 6.097 078 397 7E-11 | 9.047 251 836 5E-11 | 8.396 039 419 2E-11 |
| AMC-SFLA | 4.677 414 011 6E-12 | 8.380 762 750 4E-11 | 6.716 316 391 9E-11 |
| 函数算法 | f7 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | 0.073 873 870 8 | 0.518 902 845 9 | 0.265 534 605 6 |
| SFLA | 0.029 547 259 7 | 0.120 579 179 4 | 0.066 899 074 0 |
| NOSMC-SFLA | 2.911 171 304 0E-10 | 9.913 958 542 9E-10 | 8.956 280 161 9E-10 |
| FMC-SFLA | 4.807 199 083 2E-11 | 8.817 169 134 2E-11 | 7.397 249 479 6E-11 |
| AMC-SFLA | 6.336 875 468 8E-12 | 7.587 885 875 1E-11 | 6.319 744 644 7E-11 |
| 函数算法 | f8 | ||
| 最优结果 | 最差结果 | 平均结果 | |
| PSO | 5.969 754 342 5 | 40.793 154 638 2 | 17.710 246 24 |
| SFLA | 4.767 741 756 9E-11 | 1.989 955 939 5 | 0.597 256 704 2 |
| NOSMC-SFLA | 4.544 391 802 7E-11 | 9.625 988 812 1E-10 | 8.193 978 828 7E-10 |
| FMC-SFLA | 3.903 189 048 6E-11 | 9.379 164 112 0E-11 | 7.760 547 759 9E-11 |
| AMC-SFLA | 9.234 213 393 9E-12 | 8.222 400 538 2E-11 | 6.390 621 365 4E-11 |
通过表 9~12的运行时间和方差来评价算法优化性能,运行时间在一定程度上反映出算法的进化速度,方差可以体现算法的可靠性. 由于文中的测试函数均有多个局部极值点,在仿真结果中,PSO算法和SFLA在f4~f8的成功率不高; NOSMC-SFLA和FMC-SFLA取得了一定的成功率,但算法达到成功的运行时间均明显增多且算法可靠性不高; f1的最优、 最差和平均结果虽然一样,却是由于运算结果的保留位数所导致的; 但AMC-SFLA的成功率、 运行时间和方差都优于前几种算法,说明AMC-SFLA对高维多峰函数的求解具有很好的适应性. 同时,分析SFLA较快的原因是由于SFLA在迭代时只更新最差粒子,最好情况下一次迭代只计算1次,最坏情况则才计算3次,相对于粒子群每次迭代更新所有粒子计算量要小,所以速度快.
| 算法 | f1 | f2 | ||
| 平均时间 /s | 方差 | 平均时间 /s | 方差 | |
| PSO | 2.605 | 1.64E-14 | 33.124 | 3.17E-01 |
| SFLA | 2.537 | 3.67E-21 | 25.096 | 1.00E+00 |
| NOSMC-SFLA | 1.051 | 2.83E-21 | 8.276 | 8.13E-7 |
| FMC-SFLA | 0.635 | 2.61E-21 | 5.837 | 6.39E-9 |
| AMC-SFLA | 0.467 | 1.38E-21 | 1.752 | 5.43E-11 |
| 算法 | f3 | f4 | ||
| 平均时间 /s | 方差 | 平均时间 /s | 方差 | |
| PSO | 1.715 | 1.37E-19 | 33.405 | 3.87E+04 |
| SFLA | 1.456 | 3.69E-21 | 5.496 | 7.31E-5 |
| NOSMC-SFLA | 1.241 | 3.37E-21 | 3.382 | 8.53E-11 |
| FMC-SFLA | 0.981 | 2.93E-21 | 2.963 | 5.02E-11 |
| AMC-SFLA | 0.895 | 1.85E-21 | 1.512 | 3.99E-11 |
| 算法 | f5 | f6 | ||
| 平均时间 /s | 方差 | 平均时间 /s | 方差 | |
| PSO | 132.875 | 1.07E-05 | 144.748 | 4.90 |
| SFLA | 1.463 | 6.59E-19 | 6.981 | 3.39 |
| NOSMC-SFLA | 1.324 | 4.29E-21 | 5.231 | 7.35E-11 |
| FMC-SFLA | 0.971 | 3.91E-21 | 3.147 | 6.27E-21 |
| AMC-SFLA | 0.738 | 3.07E-21 | 1.832 | 4.61E-21 |
| 算法 | f5 | f6 | ||
| 平均时间 /s | 方差 | 平均时间 /s | 方差 | |
| PSO | 147.376 | 8.41E-02 | 139.393 | 4.12E+02 |
| SFLA5.341 | 5.21E-03 | 3.671 | 9.91E-01 | |
| NOSMC-SFLA | 4.618 | 5.26E-19 | 2.762 | 5.37E-19 |
| FMC-SFLA | 1.762 | 3.92E-21 | 1.307 | 4.71E-21 |
| AMC-SFLA | 0.937 | 2.67E-21 | 0.947 | 3.67E-21 |
针对SFLA存在早熟、 收敛速度慢且求解精度不高的缺点,本文借鉴文化算法的进化结构并引入外部空间,提出一种自适应混合文化蛙跳算法. 将反向算法、 云模型算法和混沌算法引入到信念知识和外部知识的进化过程中,并自适应调整接受函数和影响函数的作用比例,从而将3种空间有机结合,共同求取最优解. 基于高维测试函数的仿真实验结果表明,算法在整体上具有较好的全局寻优能力且收敛速度较快.
| [1] | Eusuff M M, Lansey K E. Optimization of water distribution network design using shuffled frog leaping algorithm[J]. Journal of Water Resources Planning and Management, 2003, 129(3): 210-225. |
| [2] | Elbeltagi E, Hegazy T, Grierson D. Comparison among five evolutionary-based optimization algorithms[J]. Advanced Engineering Informatics, 2005, 19(1): 43-53. |
| [3] | Amiri B, Fathian M, Maroosi A. Application of shuffled frog-leaping algorithm on clustering[J]. International Journal of Advanced Manufacturing Technology, 2009, 45(1/2): 199-209. |
| [4] | Rahimi-Vahed A, Mirzaei A H. A hybrid multi-objective shuffled frog-leaping algorithm for a mixed-model assembly line sequencing problem[J]. Computers and Industrial Engineering, 2007, 53(4): 642-666. |
| [5] | Rahimi-Vahed A, Mirzaei A H. Solving a bi-criteria permutation flow-shop problem using shuffled frog-leaping algorithm[J]. Soft Computing, 2008, 12(5): 435-452. |
| [6] | Bhaduri A. A clonal selection based shuffled frog leaping algorithm[C]//IEEE International Conference on Advance Computing. Piscataway, UJ, USA: IEEE, 2009: 125-130. |
| [7] | 李建军, 郁滨, 陈武平. 混合蛙跳算法的改进与仿真[J]. 系统仿真学报, 2014, 26(4): 755-760. Li J J, Yu B, Chen W P. Improvement and simulation for shuffled frog leaping algorithm[J]. Journal of Systems Simulation, 2014, 26(4): 755-760. |
| [8] | 陈小红, 李霞, 王娜. 多目标混合蛙跳算法中改进的种群分割方法[J]. 信号处理, 2014, 30(10): 1134-1142. Chen X H, Li X, Wang N. Improved population partitioning method in multi-objective shuffled frog leaping algorithm[J]. Journal of Signal Processing, 2014, 30(10): 1134-1142. |
| [9] | 孟庆伟. 混合蛙跳算法及其应用研究[D]. 西安: 西安电子科技大学, 2014. Meng Q W. Research on shuffled frog leaping algorithm and its application[D]. Xi'an: Xidian University, 2014. |
| [10] | 胥枫, 张桂珠, 赵芳, 等. 一种自适应交替的差分混合蛙跳优化算法[J]. 计算机工程, 2014, 40(8): 138-142. Xu F, Zhang G Z, Zhao F, et al. An adaptive alternating optimization algorithm of differential shuffled frog leaping[J]. Computer Engineering, 2014, 40(8): 138-142. |
| [11] | Reynolds R G. An introduction to cultural algorithms[C]//Proceedings of the 3rd Annual Conference on Evolutionary Programming. San Diego, NJ, USA: World Scientific Press, 1994: 131-139. |
| [12] | 高洪元, 崔闻. 文化蛙跳算法及其在频谱感知中的应用[J]. 中南大学学报: 自然科学版, 2013, 44(9): 3723-3730. Gao H Y, Cui W. Cultural frog leaping algorithm and its applications for spectrum sensing[J]. Journal of Central South University: Science and Technology, 2013, 44(9): 3723-3730. |
| [13] | 孙儒泳. 动物生态学原理[M]. 第三版. 北京: 北京师范大学出版社, 2001. Sun R Y. Principles of animal ecology[M]. 3rd ed. Beijing: Beijing Normal University Press, 2001. |
| [14] | 崔志华, 曾建潮. 微粒群优化算法[M]. 北京: 科学出版社, 2011. Cui Z H, Zeng J C. Particle swarm optimization[M]. Beijing: Science Press, 2011. |
| [15] | 刘挺, 王联国. 基于云模型的入侵杂草优化算法[J]. 计算机工程, 2014, 40(12): 156-160. Liu T, Wang L G. Invasive weed optimization algorithm based on cloud model[J]. Computer Engineering, 2014, 40(12): 156-160. |
| [16] | 苏兆品, 张婷, 张国富, 等. 基于云模型和模糊聚合的应急方案评估[J]. 模式识别与人工智能, 2014, 27(11): 1047-1055. Su Z P, Zhang T, Zhang G F, et al. Evaluation of emergency disposal schemes based on cloud model and fuzzy aggregation[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(11): 1047-1055. |
| [17] | 张英杰, 邵岁锋, Niyongabo J. 一种基于云模型的云变异粒子群算法[J]. 模式识别与人工智能, 2011, 24(1): 90-96. Zhang Y J, Shao S F, Niyongabo J. Cloud hypermutation particle swarm optimization algorithm based on cloud model[J]. Pattern Recognition and Artificial Intelligence, 2011, 24(1): 90-96. |
| [18] | Rahaman S F. Intervention in the social population space of cultural algorithm: An application in child seat vehicle safety[D]. Windsor, Canada: Windsor University, 2007. |
| [19] | Tizhoosh H R. Opposition-based learning: A new scheme for machine intelligence[C]//Proceedings of the International Conference on Computational Intelligence for Modeling Control and Automation. Piscataway, UJ, USA: IEEE, 2005: 695-701. |
| [20] | 王燕. 反向粒子群算法理论及及其应用研究[D]. 西安: 西安工程大学, 2011. Wang Y. The research of opposition-based particle swarm optimization and its application[D]. Xi'an: Xi'an Polytechnic University, 2011. |
| [21] | 郑楠, 王翔, 于浩杰, 等. 一种改进混沌萤火虫算法[J]. 计算机仿真, 2014, 31(10): 306-312. Zheng N, Wang X, Yu H J, et al. An improved firefly algorithm for solving multimodal functions[J]. Computer Simulation, 2014, 31(10): 306-312. |
| [22] | 刘金梅, 屈强. 几类混沌序列的随机性测试[J]. 计算机工程与应用, 2011, 47(5): 46-49. Liu J M, Qu Q. Randomness tests of several chaotic sequences[J]. Computer Engineering and Applications, 2011, 47(5): 46-49. |
| [23] | Poli R, Kennedy J, Blackwell T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33-57. |
| [24] | 李长云, 潘伟强, 胡盛龙. 基于均匀设计的支持向量机参数优化方法[J]. 计算机工程与科学, 2014, 36(4): 702-706. Li C Y, Pan W Q, Hu S L. Parameter optimization method of SVM based on uniform design[J]. Computer Engineering & Science, 2014, 36(4): 702-706. |



