化工过程中经常遇到不稳定时滞对象,比如反应器温度控制. 对于此类过程,由于右半平面极点和时滞的存在,闭环系统容易变得不稳定或者产生较大的超调[1]. 因此,不稳定时滞对象的控制一直受到广泛关注[2]. 一方面,虽然先进的控制理论不断提出,但是在工业现场,广泛使用的控制方案仍然是固定结构的控制器(如PID控制). 对于固定结构的控制器,我们希望控制器的参数是严格基于模型的,而且能够实现解析整定. 这样对于任一对象,一旦辨识出对象模型,我们便能轻松整定出控制器参数. 另一方面,从控制目标上可知,控制器的设计一般是在系统稳定的基础上,关心系统的设定值跟踪性能和抗扰性能. 因此我们希望设计出能同时提供良好扰动抑制和设定值跟踪的控制系统.
如果用上述两个标准评价现有的针对不稳定对象的控制器设计方法,可知这些方法尚有不足之处. 许多学者[2-4]提出了针对不稳定对象的有效单回路控制方案. 单回路控制方案虽然简单,但是这种一自由度结构中的设定值跟踪与抗负载扰动的设计没有分离,故控制器的设计不能同时获得良好的设定值跟踪性能和抗扰性能[5]. 为了解决上述问题,针对不稳定对象的二自由度控制方案相继被提出[6-7]. Lee等[8]采用麦克劳林级数将内模控制器(internal model control,IMC)展开转化为PID控制器,同时增加设定值滤波器构成二自由度控制方案,从而获得良好的设定值跟踪和扰动抑制性能,但文中没有提出具体的参数解析整定规则. Yang等[9]使用搜索算法得到PID控制器的参数. 此类方法计算量较大,同时由于没有严格的解析设计方法,使得该方法不利于现场使用. Shamsuzzoha[10]、 Rao[11]和Liu[12]等提出了针对抗扰性能的PID的设计方法. 但是,都没有详细分析控制系统的鲁棒/性能平衡问题,因此不能得到一定鲁棒条件下最优的控制器.
本文旨在设计出同时提高设定值跟踪和干扰抑制的控制器,并且得到控制器的解析整定规则. Liu[12]提出了一种基于内模原理的二自由度控制方案,该方案得到了较多研究者的认可[13]. 然而,文中并没有详述控制器参数与系统输出性能、 鲁棒性之间的关系,也没有提供控制参数的解析整定规则. 本文利用该文的控制结构,采用一种加强的内模滤波器,深入分析控制器参数和系统鲁棒性、 输出性能的关系. 在稳定的前提下,控制器的设计本质为系统鲁棒性和输出性能的折中. 本文用最大灵敏度函数(maximum sensitivity function,Ms)评价系统的鲁棒性,用积分绝对误差(integral absolute error,IAE)评价系统的输出性能. 如此,控制器的设计转换成一定鲁棒指标下,最小化IAE值的约束优化问题. 对于稳定系统,许多文献报道了Ms合理的取值范围. 例如著名学者Astrom[14]建议Ms取值范围在1.6~2.0之间时,能实现良好鲁棒/性能折中. 然而该结论并不适合不稳定时滞对象,因为对于大时滞的不稳定对象,不存在固定结构的控制器使得系统获得该范围的Ms值. 鉴于此,本文提出一种不稳定时滞对象的Ms选取方案. 该选择规则严格依赖于对象信息. 基于此规则,我们提出了满足该Ms条件下的最优内模控制器解析设计规则,实现了不稳定时滞对象的控制器解析设计. 该方法能实现良好的鲁棒/性能平衡,同时使我们对不稳定时滞对象的内模控制设计有了更加全面的理解. 最后通过两个例子证明该方法的可行性和优越性.
2 问题描述本文考虑如下的不稳定时滞对象:
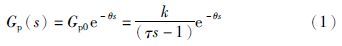
该系统的输入输出关系
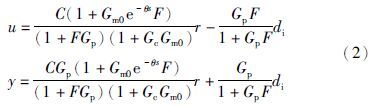
模型匹配时,上述关系式简化为
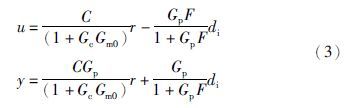
由上面的关系可知,控制器Gc将不稳定对象反馈为稳定对象,系统扰动抑制回路的稳定性只由控制器F的稳定性决定. 由式(3)可知,扰动抑制能力仅由控制器F决定,设定值跟踪性能由C和Gc决定. 系统的设定值跟踪和扰动抑制控制器可以独立进行设计. 因此,本文先根据系统的设定值跟踪性能设计控制器C,然后根据系统稳定性、 鲁棒性和抗扰能力设计控制器F.
稳定控制器Gc用来镇定不稳定对象,则设定值跟踪回路的广义控制对象为Gp0e-θs/(1+GcGp0).
针对式(1)所示的一阶不稳定对象,显而易见控制器Gc只需要比例控制器来镇定不稳定对象. 镇定后,系统的广义控制对象变为ke-θs/(τs-1+Gck). 可以简单地令τs-1+kGc=τs+1,则镇定控制器为Gc=2/k.
由式(3)可知,模型匹配时系统相当于开环,又Gc将不稳定对象反馈为稳定对象,则设定值跟踪控制器C根据常规的内模控制方法进行设计即 由此可知设定值跟踪只与参数λc有关. 随着参数λc的增大,设定值跟踪性能越来越差,鲁棒性越来越好. 根据需要的性能选取对应λc的值. 由于设定值跟踪回路中将对象反馈为稳定对象,参数整定较简单. 然而抗扰控制器F的设计需要满足系统内部稳定性及鲁棒性,使得抑制负载扰动性能较差. 本文将重点研究控制器F的设计及参数整定.
由此可知设定值跟踪只与参数λc有关. 随着参数λc的增大,设定值跟踪性能越来越差,鲁棒性越来越好. 根据需要的性能选取对应λc的值. 由于设定值跟踪回路中将对象反馈为稳定对象,参数整定较简单. 然而抗扰控制器F的设计需要满足系统内部稳定性及鲁棒性,使得抑制负载扰动性能较差. 本文将重点研究控制器F的设计及参数整定.
基于内模原理对抗负载扰动控制器进行设计,如图 2所示.

|
| 图 2 二自由度内模控制系统 Fig. 2 Two-degree-of-freedom IMC system |
图 2中Gm为对象模型,Q表示内模控制器. 根据内模控制原理,Q设计如下:
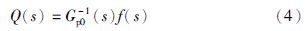
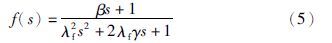
根据内模控制原理得到抗负载扰动控制器:
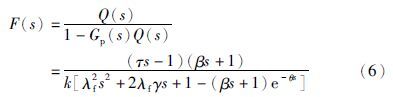
利用麦克劳林公式将控制器近似为标准的PID控制器. 控制器F可以表示为

麦克劳林序列将控制器展开成以下形式:
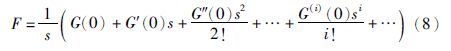


针对一阶不稳定对象PID控制器参数为<
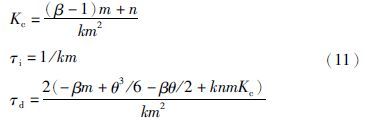
由图 1可知,反馈控制器直接决定系统扰动抑制回路稳定性、 系统的鲁棒性和抗扰性能. 因此,抗扰控制器F的设计实质上是在保证系统稳定的前提下,实现鲁棒与性能的折中.
3.1 系统内部稳定性根据系统内部稳定性[4]的定义,当且仅当式(12)稳定时,系统内部稳定.
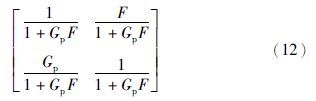
上述稳定条件等价为
(1)  稳定;
稳定;
(2) F稳定;
(3)  稳定.
因此,为了保持系统内部稳定,系统控制器设计必须满足条件:
稳定.
因此,为了保持系统内部稳定,系统控制器设计必须满足条件:

将式(1),式(6)带入式(13)得到:
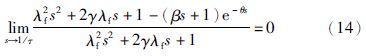
随着系统运行条件和时间的不同,系统辨识模型通常不精准,系统鲁棒性尤为重要. 最大灵敏度函数Ms具有明确的物理意义,因此被一些文章用来进行鲁棒性分析. 本文也采用Ms来分析,Ms表述为

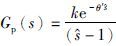 ,这里θ′=
,这里θ′=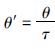 . 由式(3)可知,扰动抑制回路的开环传递函数为
. 由式(3)可知,扰动抑制回路的开环传递函数为
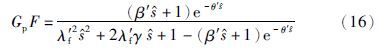
归一化后系统最大灵敏度函数表示为
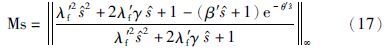
针对归一化后的不稳定对象,参数β′与可调参数的关系变为β′=(λf′2+2λ′fγ+1)eθ′-1. 由此可知,针对归一化后的对象,最大灵敏度函数与λ′f,γ及θ′有着直接的关系.
3.3 抗扰性能指标由式(3)可知,系统的扰动响应为
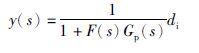
考虑常见的单位阶跃扰动信号,即d=$\frac{1}{s}$. 用IAE指标来估计系统的抗负载扰动的闭环性能,其定义为
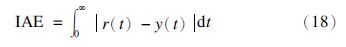
系统加入负载扰动信号,调节控制器参数使系统达到最优的IAE性能指标IAEld0,控制器设计过程中考虑鲁棒性,必然使得性能下降即IAE≥IAEld0. 为了实现鲁棒性与性能的折中,则采用梯度性能指标来衡量.
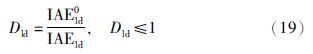
首先考虑可调参数对性能及鲁棒性的影响,图 3表明可调参数对系统性能的影响. 观察图 3可以发现,随着可调参数λ′f的增大,其性能指标IAEld先减小后增大.

|
| 图 3 θ′=0.05,0.4,0.9,1.3时可调参数与系统性能的关系 Fig. 3 Relationship between performance and adjustable paramater θ′ when θ′=0.05,0.4,0.9,1.3 |
图 4为可调参数λ′f与鲁棒性Ms的对应关系图. 观察图 4可以发现θ′较大时,参数γ=1时,系统具有更广泛的灵敏度函数取值范围.

|
| 图 4 θ′=0.05,0.4,0.9,1.3时可调参数与Ms的关系 Fig. 4 Relationship between Ms and adjustable paramater θ′ when θ′=0.05,0.4,0.9,1.3 |
图 5为系统鲁棒性与梯度性能指标的对应关系. 由图 5可知,对于一个给定的θ′,随着鲁棒性Ms的增加,系统性能指标IAE先不断地减小达到最优再增大,使得不稳定对象的参数整定尤为重要. 在相同的鲁棒性下,不同的γ取值有不同的性能. 当γ=1时,本文方法等同于Liu的方法[12]. 观察图 5,对于θ′较大的对象,当γ=1时系统具有更为广泛的Ms取值范围,但当期望的性能下降到Dld=0.8时,系统的鲁棒性较差. 图 5清晰地表明通过给定系统鲁棒指标能实现系统鲁棒性与性能折中.

|
| 图 5 θ′=0.05,0.4,0.9,1.3时梯度性能指标与Ms的关系 Fig. 5 Relationship between Ms and degraded performance θ′ when θ′=0.05,0.4,0.9,1.3 |
针对稳定对象的鲁棒性与性能的关系已有很多研究[14-18],同时给出参数整定时的目标Ms值Mst=1.6. 与稳定对象相比较,由于控制器设计需要满足内部稳定性即加入一个约束条件,使得无法找到一个目标最大灵敏度函数值适用于θ′<1.5的所有对象. 观察图 5可以发现,不稳定对象在1.4≤Ms<2范围内,其性能下降比较大,造成抑制负载扰动性能较差. 对于参数θ′较大的对象,Ms无法达到1.4~2的范围内. 因此,针对不稳定对象,Ms<2的规则已经不再适用. 为了更好地实现鲁棒性与性能的平衡,选取减小最优性能20%即Dld=0.8时的Ms值作为目标最大灵敏度函数实现鲁棒性与性能折中.
分析θ′从0到1.5变化时,γ的选取对鲁棒性及性能影响. 满足式(20)得到最优的γ值.
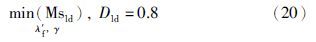
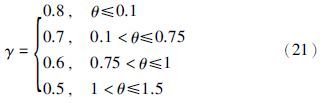
针对不同的θ′,选取Dld=0.8时的Ms值作为目标最大灵敏度函数Mst. 图 6为不同θ′情况下的的Mst取值. 由图 6可知,不稳定对象的鲁棒性与θ′有着密切的联系,随着θ′的增大,Mst也不断增大.

|
| 图 6 θ′与Mst的关系 Fig. 6 Relationship between Mst and θ′ |
将图 6中Mst与θ′的关系进行曲线拟合,得到基于模型信息的鲁棒指标为
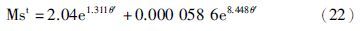
式(22)给出了目标最大灵敏度函数与对象θ′的解析表达式,通过已知对象的θ′就可以简单求得对应的Mst.
目标最大灵敏度函数Mst给定后,基于对象信息抗负载扰动控制器参数λ′f可以唯一确定,如图 7所示.

|
| 图 7 可调参数λ′f与θ′的关系 Fig. 7 Relationship between adjustable λ′f and θ′ |
将可调参数与对象归一化的时滞θ′的对应关系拟合为
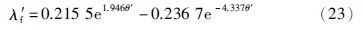
基于目标最大灵敏度函数Mst,式(23)给出了抗扰控制器可调参数λ′f的解析表达式.
抗扰控制器F的设计步骤总结如下:
(1) 基于内模原理进行控制器设计;
(2) 根据对象的时滞与时间常数的比值θ′,按照式(21)选取参数γ;
(3) 依据θ′,由式(22)可以得到目标最大灵敏度函数Mst;
(4) 最后由式(23)求出可调参数的取值.
本文选取性能下降程度Dld=0.8时的灵敏度函数为目标最大灵敏度函数Mst,在此灵敏度函数的条件下,得到控制器参数整定解析式. 根据本文的方法,可以得到其他Mst的水平下,控制器可调参数的解析表达式.
4 仿真
本文使用波动总和TV估计对象输入信号的波动,TV的定义如下: ,TVsp为系统加入设定值时,对象输入信号的波动总和,TVld为系统加入负载扰动时,对象输入信号的波动总和. IAEsp为系统加入设定值时,系统的IAE性能指标. IAEld为系统加入负载扰动信号时,系统的IAE性能指标.
,TVsp为系统加入设定值时,对象输入信号的波动总和,TVld为系统加入负载扰动时,对象输入信号的波动总和. IAEsp为系统加入设定值时,系统的IAE性能指标. IAEld为系统加入负载扰动信号时,系统的IAE性能指标.
例1 在这部分,我们考虑经典的积分时滞对象,对象可以表示为

许多方法针对IPTD进行了控制器设计,现选取MoReRT[19]和经典的SIMC[20]与本文的方法进行比较. 为了达到与MoReRT中相近的设定值跟踪效果,文中λc选取10. 本文的控制器设计针对不稳定对象,所以将上述对象近似为

针对该不稳定对象,根据式(21)选取参数γ=0.8. 系统控制器参数及性能见表 1. 图 8为标况下3种方法的阶跃响应曲线图,其中当仿真时间t=0 s时,加入幅值为1的设定值阶跃响应; 仿真时间t=200 s时,加入幅值为1的阶跃扰动. 由图 8可知,在相同的鲁棒性下,本文方法的抗负载扰动性能有了显著的提升. MoReRT的方法对此类对象扰动抑制没有明显的优势. SIMC的方法参数整定简单,但其不是最优的控制器,抗负载扰动性能较差.
| Kc | τi | τd | IAEsp | TVsp | IAEld | TVld | Ms | |
| 本文(Ms=2) | 0.539 3 | 0.039 3 | 2.146 8 | 16.526 8 | 1 | 56.114 4 | 1.859 8 | 2.0 |
| MoReRT | 0.382 4 | 0.010 7 | / | 18.822 0 | 0.550 5 | 91.757 8 | 1.916 4 | 2.0 |
| 本文(Ms=1.7) | 0.409 8 | 0.031 0 | 1.781 1 | 16.526 8 | 1 | 100.869 5 | 1.564 0 | 1.7 |
| SIMC | 0.338 0 | 0.005 7 | / | 30.020 2 | 0.406 8 | 173.509 7 | 1.555 7 | 1.7 |

|
| 图 8 例1模型匹配时响应曲线 Fig. 8 Response curves when example 1 model matching |
为了验证系统鲁棒性,将对象的增益加入20%的不确定性,同时时滞加入20%的不确定性即p=0.24e-8.88s/s. 图 9为模型失配时,系统阶跃响应曲线. 系统模型失配时,仍能保持良好的性能. 本例证明了该方法适用于纯积分对象.

|
| 图 9 例1模型失配时阶跃响应曲线 Fig. 9 Step response curves when example 1 model mismatch |
例2 本文考虑一个等温化学反应器[11],该反应器可以用以下不稳定传递函数来表示:

根据式(21),选取γ=0.7,得到鲁棒性及负载扰动性能与可调参数λ′f的对应关系,如图 10所示.

|
| 图 10 θ′=0.2时对象可调参数与Ms,IAEld的关系曲线 Fig. 10 Response curves between Ms, IAEld and adjustable parameter θ′ when θ′=0.2 |
将图 10中可调参数与鲁棒性的对应函数关系拟合为
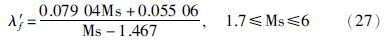
在式(27)的基础上,针对θ/τ≈0.2的对象,我们可以通过选择任意的最大灵敏度函数值实现鲁棒性与性能的折中.
将本文的方法与Rao[11]和Liu[12]的方法进行比较,在Rao的方法中,Ms=3.65. 为了公平比较,本文及Liu的方法整定与Rao有相同的Ms. 控制器参数及性能指标见表 2. 为了使Rao与其他方法有几乎相同的设定值跟踪,取设定值权值为0.5. 模型精确的情况下,系统的单位阶跃曲线如图 11所示,其中当仿真时间t=0 s时,加入幅值为1的设定值阶跃响应; 仿真时间t=300 s时,加入幅值为1的阶跃扰动. 由图 11可知,在相同的Ms情况下,本文方法具有更好的抗负载扰动性能. 图 12为系统时滞失配30%时,系统的阶跃响应图.
| Kc | τi | τd | IAEsp | TVsp | IAEld | TVld | Ms | |
| 本文(Ms=2.86) | 1.568 | 0.023 0 | 10.861 | 39.751 | 3.294 | 46.619 | 3.171 | 2.86 |
| 本文(Ms=3.65) | 1.812 | 0.030 0 | 13.522 | 39.751 | 3.294 | 35.838 | 4.042 | 3.65 |
| Liu | 1.812 | 0.025 9 | 14.560 | 39.751 | 3.294 | 39.074 | 4.088 | 3.65 |
| Rao | 1.017 | / | 21.022 | 40.956 | 3.085 | 55.225 | 5.964 | 3.65 |

|
| 图 11 例2模型标配时系统阶跃响应 Fig. 11 System step response curves when example 2 model matching |

|
| 图 12 例2模型失配时系统阶跃响应 Fig. 12 System step response curves when example 2 model mismatch |
本文提出了一种针对不稳定对象的最优鲁棒二自由度控制器解析设计方法,在内模控制的基础上,改进内模控制器的滤波器结构提升系统的扰动抑制性能及鲁棒性. 基于目标最大灵敏度函数给出抗扰控制器参数整定解析式,实现鲁棒性与性能的平衡,得到最优负载扰动控制器. 本文的方法适用于一阶不稳定对象及积分对象. 仿真例子证明了该方法的有效性.
| [1] | Rao A S, Chidambaram M. Enhanced Smith predictor for unstable processes with time delay[J]. Industrial & Engineering Chemistry Research, 2005, 44(22): 8291-8299. |
| [2] | Park J H, Sung S W, Lee I B. An enhanced PID control strategy for unstable processes[J]. Automatica, 1998, 34(6): 751-756. |
| [3] | Rotstein G E, Lewin D R. Simple PI and PID tuning for open-loop unstable systems[J]. Industrial & Engineering Chemistry Research, 1991, 30(8): 1864-1869. |
| [4] | Morari M, Zaflriou E. Robust process control[M]. Upper Saddle River, NJ, USA: Prentice Hall, 1989: 85-110. |
| [5] | Jin Q B, Liu Q. Analytical IMC-PID design in terms of performance/robustness tradeoff for integrating processes: From 2-Dof to 1-Dof[J]. Journal of Process Control, 2014, 24(3): 22-32. |
| [6] | Nasution A A, Jeng J C, Huang H P. Optimal H-2 IMC-PID controller with set-point weighting for time-delayed unstable processes[J]. Industrial & Engineering Chemistry Research, 2011, 50(8): 4567-4578. |
| [7] | Tan W, Marquez H J, Chen T W. IMC design for unstable processes with time delays[J]. Journal of Process Control, 2003, 13(3): 203-213. |
| [8] | Lee Y, Lee J, Park S. PID controller tuning for integrating and unstable processes with time delay[J]. Chemical Engineering Science, 2000, 55(17): 3481-3493. |
| [9] | Yang X P, Wang Q G, Hang C C, et al. IMC-based control system design for unstable processes[J]. Industrial & Engineering Chemistry Research, 2002, 41(17): 4288-4294. |
| [10] | Shamsuzzoha M, Lee M. Analytical design of enhanced PID filter controller for integrating and first order unstable processes with time delay[J]. Chemical Engineering Science, 2008, 63(10): 2717-2731. |
| [11] | Rao A S, Rao V S R, Chidambaram M. Simple analytical design of modified Smith predictor with improved performance for unstable first-order plus time delay (FOPTD) processes[J]. Industrial & Engineering Chemistry Research, 2007, 46(13): 4561-4571. |
| [12] | Liu T, Zhang W D, Gu D Y. Analytical design of two-degree-of-freedom control scheme for open-loop unstable processes with time delay[J]. Journal of Process Control, 2005, 15(5): 559-572. |
| [13] | Shamsuzzoha M, Lee M. Enhanced disturbance rejection for open-loop unstable process with time delay[J]. ISA Transactions, 2009, 48(2): 237-244. |
| [14] | Astrm K J, Hägglund T. PID controllers: Theory, design, and tuning[M]. Research Triangle Park, NC, USA: Instrument Society of America, 1995. |
| [15] | 赵志诚, 刘志远, 张井岗. 一种时滞过程内模PID控制器鲁棒整定方法[J]. 信息与控制, 2010, 39(5): 526-530. Zhao Z C, Liu Z Y, Zhang J G. A robust tuning method of internal model PID controller for process with time-delay[J]. Information and Control, 2010, 39(5): 526-530. |
| [16] | Alcántara S, Zhang W D, Pedret C, et al. IMC-like analytical H∞ design with S/SP mixed sensitivity consideration: Utility in PID tuning guidance[J]. Journal of Process Control, 2011, 21(6): 976-986. |
| [17] | Arrieta O, Vilanova R. Servo/Regulation tradeoff tuning of PID controllers with a robustness consideration[C]//2007 46th IEEE Conference on Decision and Control. Piscataway, UJ, USA: IEEE, 2007: 1838-1843. |
| [18] | Jin Q B, L Q, Wang Q, et al. PID controller design based on the time domain information of robust IMC controller using maximum sensitivity[J]. Chinese Journal of Chemical Engineering, 2013, 21(5): 529-536. |
| [19] | Alfaro V M, Vilanova R. Robust tuning and performance analysis of 2DoF PI controllers for integrating controlled processes[J]. Industrial & Engineering Chemistry Research, 2012, 51(40): 13182-13194. |
| [20] | Skogestad S. Simple analytic rules for model reduction and PID controller tuning[J]. Journal of Process Control, 2003, 13(4): 291-309. |




