网络控制系统(NCS)由于具有安装维护方便、 灵活性高和易于重构等优点,近年来得到了广泛的应用[1-4]. 但是由于网络的带宽总是有限的,所以数据包在通过网络传输的过程中不可避免地发生碰撞,发送前有时还需要排队等候,这样将会诱发网络传输时延、 数据包丢失以及时序错乱等现象[5-9]. 此外,由于数据在通过网络传输之前,要进行格式转化,一般对数据的量化是必要的,量化操作将会带来量化的误差[10-12].
现有的鲁棒控制方法大多只考虑了被控对象和外扰的不确定性[13],而在实际的NCS中,由于工业仪表、 控制元件受到本身物理特性及环境因素的影响[14],导致控制器参数存在一定的误差或变化,而控制器参数微小的摄动都可能导致闭环系统性能下降,甚至稳定性遭到破坏,因此设计对其自身参数摄动不敏感或非脆弱的控制器具有重要意义. 文[15-17]分别介绍了针对存在区间时滞的NCS的非脆弱H∞保成本控制器、 NCS非脆弱保性能分析、 非脆弱H∞保性能控制器设计方法.
上述文献主要研究了NCS的鲁棒控制问题和具有时延的NCS的非脆弱控制问题,关于带有随机丢包和量化误差的不确定离散NCS的非脆弱量化H∞控制的相关研究相对较少. 本文综合考虑了随机丢包、 量化误差、 系统参数和控制器增益的不确定性对离散NCS的影响,基于李亚普诺夫稳定性理论,设计了在容许的参数摄动、 丢包概率和量化密度下闭环NCS的非脆弱H∞控制器,控制器满足H∞性能指标.
2 问题描述
以随机丢包非线性网络化控制系统为研究对象,假设传感器—控制器和控制器—执行器两个传输通道均存在随机丢包,用满足Bernoulli 0-1序列分布的随机变量αk和βk来表示两通道上的丢包情况[
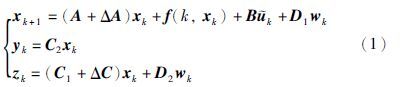
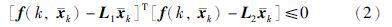
ΔA和ΔC是参数不确定部分,具有如下形式
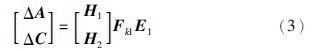

在网络化控制系统中,为了减轻网络负载,测量信号在通过网络传输之前需要进行量化. 在这里,使用对数量化器[17],具体定义为
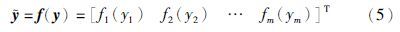
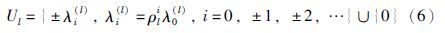
对于对数量化器,量化域中的每一个片段与量化水平集中的某一个元素λi(l)相对应,量化器将整个量化域映射到这个量化水平集. 对数量化器f(·)的分量fl(·)是如下定义的
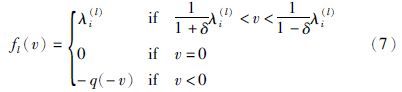
定义量化误差为
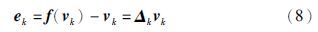
本文中,定义传感器—控制器和控制器—执行器的量化误差
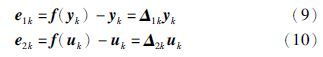
假定ρ1=ρ2=ρ,因此有δ1=δ2=δ,Δ1k=Δ2k=Δk,测量输出和控制输入可以通过式(11)、 式(12)的形式给出:

对系统(1),考虑设计如下形式的基于观测器的状态反馈控制器:
观测器:
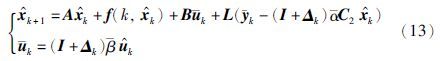
控制器:
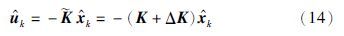


定义系统估计误差:

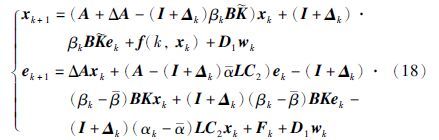
令ηk=[xk ek]T,闭环网络非线性系统(18)可以描述成如下形式:
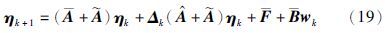
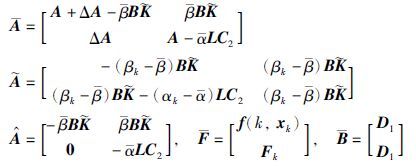
定义1 当wk=0时,如果存在两个常数σ>0和ζk∈(0,1),对所有的η(0)∈Rn,k∈I+(I+为正整数)满足
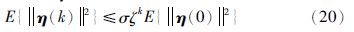
本文的主要目的是为不确定系统(1)设计观测器(13)和控制器(14),使所设计的控制器在容许的增益摄动和丢包概率下,仍能满足如下(Q1)和(Q2)两个性能要求:
(Q1) 闭环系统(10)均方指数稳定.
(Q2) 在零初始条件下,对于任意的非零wk,控制输出zk满足
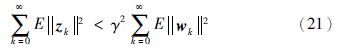
假设1 矩阵B是列满秩,如rank(B)=m,则存在两个正交矩阵U∈Rn×m和V∈Rm×n,使得
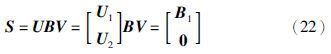
引理1[18] 对于列满秩矩阵B∈Rn×m,如果矩阵P是正定对称矩阵,那么,存在非奇异矩阵P1∈Rm×m使矩阵等式BP1=PB成立,当且仅当
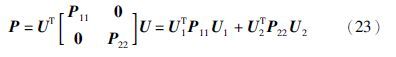
引理2[19] 给定合适维数的矩阵M=MT、 H、 E,对任意满足FTF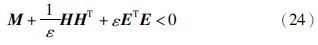
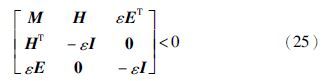
定理1 考虑到闭环系统(19)具有给定的量化密度ρ,给定信号传输通道参数0≤≤1和0≤≤1,如果存在正定矩阵P>0、 Q>0满足引理2,非负实数τ1≥0、 τ2≥0,满足矩阵不等式(26),那么系统(19)是均方指数稳定的,其中,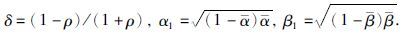 .
.
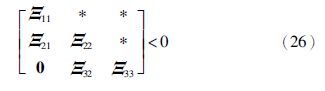
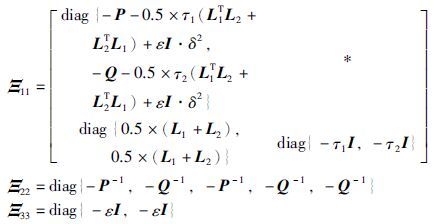
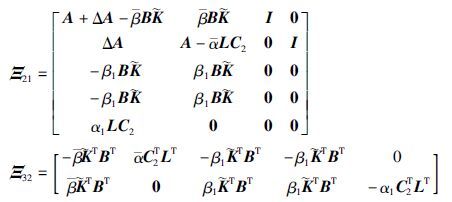
证明 令‖Δk‖2<δ2,根据引理2,式(26)可以写成式(27)的形式.
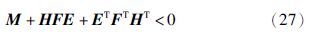
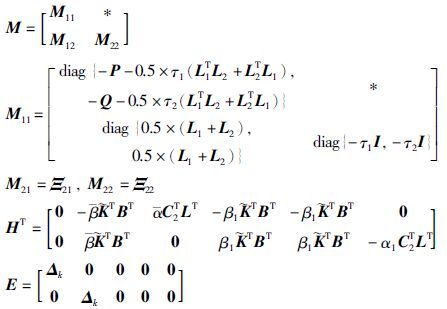
定义如下形式的李亚普诺夫函数
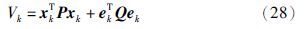
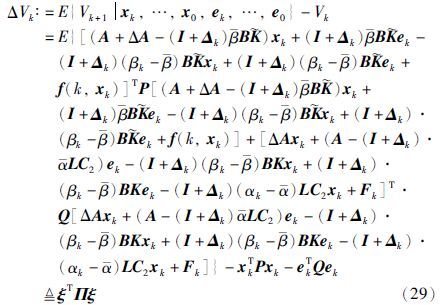
注意到E{(αk-${\bar{\alpha }}$)2}=(1-${\bar{\alpha }}$)${\bar{\alpha }}$,E{(βk-${\bar{\beta }}$)2}=(1-${\bar{\beta }}$)${\bar{\beta }}$,有

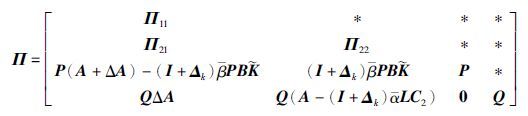
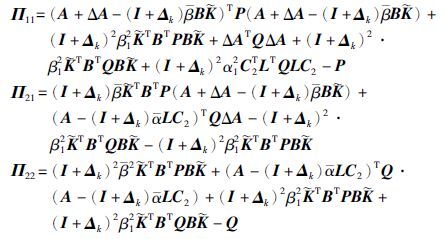
由式(2)有,
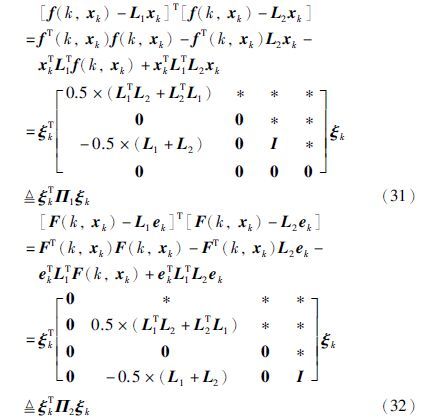
由S-procedure引理有,如果存在正定矩阵P>0,Q>0,以及τ1≥0,τ2≥0,使得
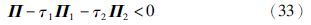

由Schur补引理,式(33)等价于式(27),因此,有ΔVk=ξTkΠξk<0,Π<0.
通过式(30)和Π<0可知
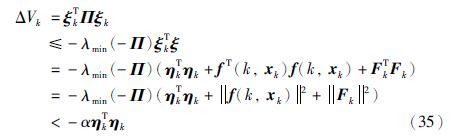
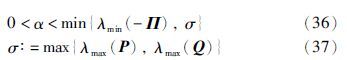
由式(36)和式(37),有
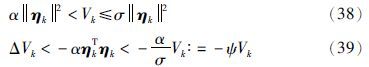
定理2 考虑到闭环系统(19)具有给定的量化密度ρ,给定信号的传输通道参数0≤${\bar{\alpha }}$≤1和0≤${\bar{\beta }}$≤1,标量λ>0,如果存在正定矩阵P>0,Q>0,非负实数τ1≥0,τ2≥0,满足矩阵不等式(40),那么系统(19)是均方指数稳定的,同时对任意wk≠0满足H∞性能指标(21).
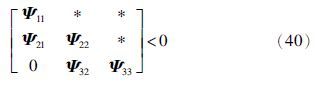

证明 由于式(40)确保式(26)成立,所以不确定系统(19)是均方指数稳定的.
下面对任意wk≠0,由式(18)有,
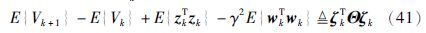

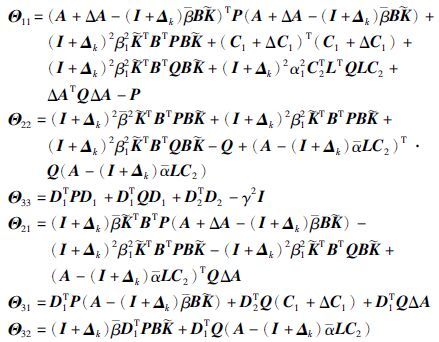
同定理1的证明有,

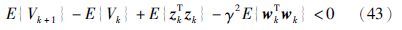
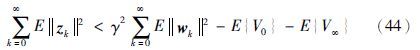
由于闭环网络化控制系统(19)指数均方稳定,并且初始条件η0=0,得:
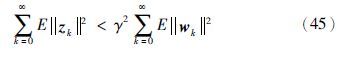
定理3 考虑到闭环系统(19)具有给定的量化密度ρ,给定通信网络的通道参数0≤${\bar{\alpha }}$≤1和0≤${\bar{\beta }}$≤1,标量λ>0,在假设1的情况下,如果存在正定矩阵P11∈Rm×m,P22∈R(n-m)×(n-m),Q∈Rn×n,实矩阵M∈Rm×n,N∈Rn×p,非负标量τ1≥0,τ2≥0,满足矩阵不等式(46),则闭环非线性不确定系统(19)均方指数稳定,及非脆弱鲁棒H∞控制器存在,其中ε1>0,ε2>0.

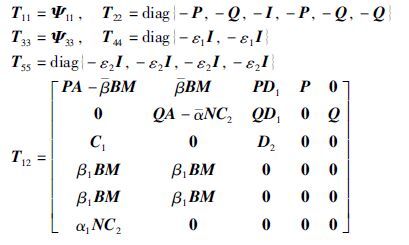
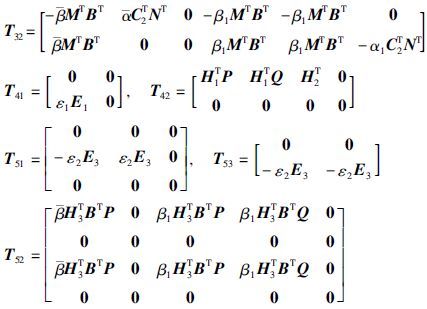
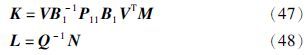
证明 式(40)可以写成式(49)的形式:

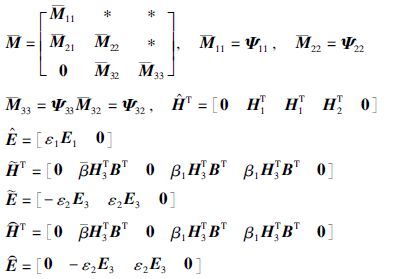
根据引理2,式(49)等价于式(50),ε1>0,ε2>0
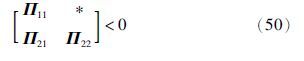
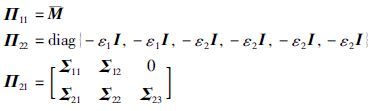
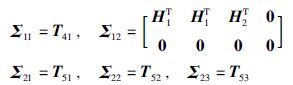
注意到,矩阵变量P和K,Q和K,Q和L在式(50)中都是以非线性的形式出现的,因此该矩阵不等式不能够用Matlab LMI工具箱来求解,需要将非线性矩阵不等式转换为线性矩阵不等式.
由于存在矩阵P11>0,P22>0,满足P=Q=U1TP11U1+U2TP22U2,由引理1知,存在非奇异矩阵P1∈Rm×m,使得矩阵等式BP1=PB成立. 现在通过关系BP1=PB,求出矩阵P1
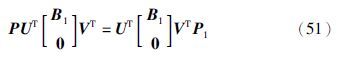
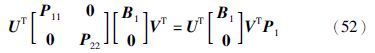
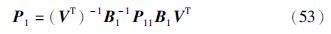
在式(46)的两边同时乘以对角阵diag(I,I,I,I,I,P-1,Q-1,I,P-1,Q-1,Q-1,I,I,I,I,I,I,I,I),同时M=P1K,N=QL,则容易看出式(46)等价于式(50). 所以闭环非线性不确定系统(19)指数均方稳定,控制器的增益
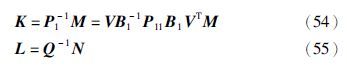
为验证文本所提方法的有效性,给出了一个具体系统进行仿真验证,系统模型是由不间断电源(uninterruptable power supply,UPS)组成的网络系统控制问题抽象而来的[16],如下所示.
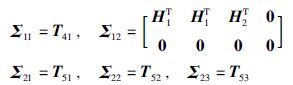
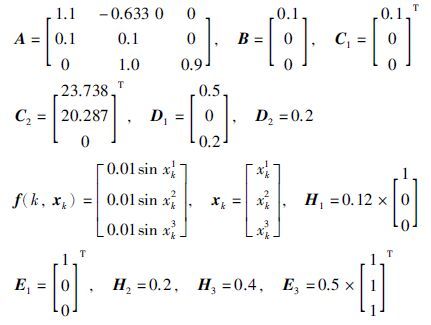
矩阵A的特征值为0.900 0,0.167 9,1.032 1,所以原开环系统是不稳定的. 很容易验证非线性函数f(k,xk)满足扇形界条件(2).
假定网络化非线性参数不确定系统(1)的初始状态为x0=[0.2 0.3 0.1]T,${\hat{x}}$0=[0 0 0]T,扰动输入wk=1/(0.1+k2).
取量化密度ρ=0.95,从传感器—控制器和从控制器—执行器端网络的丢包概率分别为1-和1-,将给出3种不同的丢包概率,通过定理3设计了3个相应的控制器满足H∞性能指标γ最小. 应用Matlab LMI工具箱求解并优化得到不同丢包概率情况下的传统控制器参数和非脆弱控制器参数,利用γ=Σ(‖zk‖)/Σ(‖wk‖)分别求出对应的H∞性能指标γ,在表 1中给出.
| 1-${\bar{\alpha }}$ | 1-${\bar{\beta }}$ | 控制器类别 | K | L | γ |
| 0.05 | 0.05 | 传统 | [3.410 8 -0.155 3 0.200 4] | [0.071 1 0.005 0 -0.000 9]T | 0.696 0 |
| 0.05 | 0.05 | 非脆弱 | [3.355 0 -0.120 1 0.123 5] | [0.052 0 0.004 1 -0.000 9]T | 0.570 7 |
| 0.05 | 0.10 | 传统 | [3.475 2 -0.987 5 0.250 5] | [0.069 9 0.005 0 -0.001 6]T | 0.987 8 |
| 0.05 | 0.10 | 非脆弱 | [3.366 8 -0.095 3 0.142 2] | [0.051 3 0.004 0 -0.000 4]T | 0.816 8 |
| 0.10 | 0.10 | 传统 | [3.759 8 -0.009 4 0.000 2] | [0.067 5 0.004 9 -0.002 4]T | 1.218 9 |
| 0.10 | 0.10 | 非脆弱 | [3.367 5 -0.005 2 0.127 9] | [0.049 6 0.004 0 -0.000 4]T | 1.046 8 |
取传感器—控制器和从控制器—执行器端网络的丢包概率分别为0.95和0.95,将给出3种不同的量化密度,通过定理3设计了3个相应的控制器满足H∞性能指标γ最小. 应用Matlab LMI工具箱求解并优化得到不同量化密度下的传统控制器参数和非脆弱控制器参数,利用γ=Σ(‖zk‖)/Σ(‖wk‖)分别求出对应的H∞性能指标γ,在表 2中给出.
| 量化密度ρ | 量化误差 | 控制器类别 | K | L | γ |
| 0.93 | [-0.036 3,0.036 3] | 传统 | [3.515 8 -0.126 3 0.001 1] | [0.072 1 0.003 0 -0.007 4]T | 1.796 0 |
| 0.93 | [-0.306 3,0.036 3] | 非脆弱 | [3.333 3 -0.110 5 0.127 7] | [0.051 1 0.004 1 -0.000 7]T | 0.597 0 |
| 0.90 | [-0.052 6,0.052 6] | 传统 | [3.624 2 -0.786 5 0.000 5] | [0.070 9 0.003 5 -0.000 9]T | 5.207 8 |
| 0.90 | [-0.052 6,0.052 6] | 非脆弱 | [3.401 4 -0.103 5 0.132 2] | [0.049 8 0.004 0 -0.000 4]T | 3.395 1 |
| 0.87 | [-0.069 5,0.069 5] | 传统 | [3.835 4 -0.301 4 0.000 2] | [0.059 5 0.003 8 -0.001 9]T | 8.218 9 |
| 0.87 | [-0.069 5,0.069 5] | 非脆弱 | [3.670 3 -0.104 1 0.134 4] | [0.048 5 0.003 9 -0.000 1]T | 6.985 7 |
从表 1和表 2可以看出,无论系统采用传统控制器还是非脆弱控制器,随着网络通道中丢包概率增大(量化密度减小),系统的H∞性能指标γ也随之增大,这说明丢包概率(量化密度)对系统的性能是有重要影响的; 而且在同一个丢包概率(量化密度)下,采用非脆弱控制器的H∞性能指标γ明显比传统控制器的性能指标γ小,说明本文中采用非脆弱控制器较传统控制器有更好的扰动抑制性能.
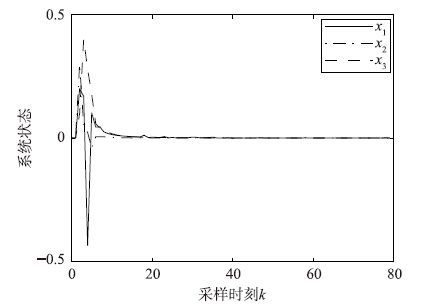
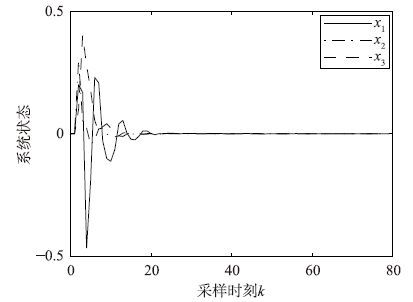
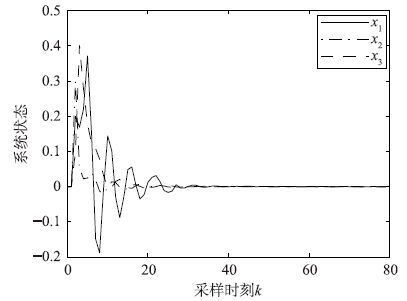
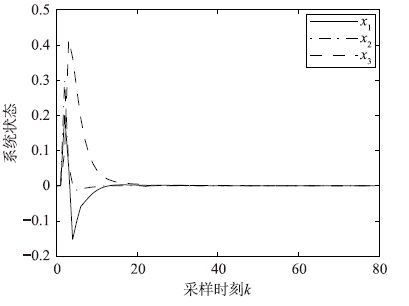
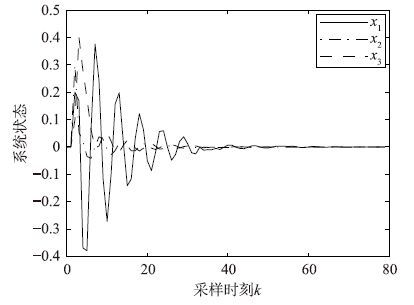
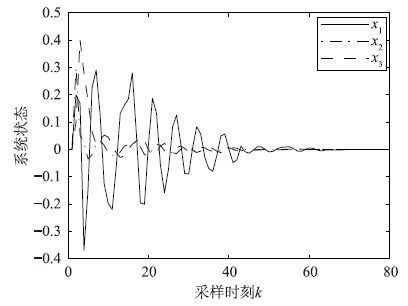
引入增益摄动后,系统在3种丢包概率情况下的非脆弱鲁棒控制状态响应如图 1~3所示,系统在3种量化密度情况下的非脆弱鲁棒控制状态响应如图 4~6所示.
|
| 图 1 γ=0.570 7时的非脆弱量化H∞控制状态响应 Fig. 1 Response of non-fragile quantized H∞ control with γ=0.570 7 |
|
| 图 2 γ=0.816 8时的非脆弱量化H∞控制状态响应 Fig. 2 Response of non-fragile quantized H∞ control with γ=0.816 8 |
|
| 图 3 γ=1.046 8时的非脆弱量化H∞控制状态响应 Fig. 3 Response of non-fragile quantized H∞ control with γ=1.046 8 |
|
| 图 4 γ=0.559 7时的非脆弱量化H∞控制状态响应 Fig. 4 Response of non-fragile quantized H∞ control with γ=0.559 7 |
|
| 图 5 γ=3.395 1时的非脆弱量化H∞控制状态响应 Fig. 5 Response of non-fragile quantized H∞ control with γ=3.395 1 |
|
| 图 6 γ=6.985 7时的非脆弱量化H∞控制状态响应 Fig. 6 Response of non-fragile quantized H∞ control with γ=9.985 7 |
由上述仿真曲线可以看出,系统加入增益摄动后的状态响应曲线最终均趋向于0,说明加入非脆弱鲁棒控制器后的闭环系统(1)均方指数稳定,而且H∞性能指标γ越大,系统达到稳定的时间越长,说明了丢包概率和量化密度对系统的稳定性是有影响的.
6 结语本文研究了带有随机丢包和量化误差的不确定离散NCS的非脆弱鲁棒H∞控制问题,基于李亚普诺夫稳定性理论,利用线性矩阵不等式(LMI)处理技术得出了存在随机丢包和量化误差的非脆弱鲁棒H∞控制器存在的充分条件,所设计的非脆弱控制器在容许的参数摄动、 丢包概率和量化密度下,不仅能保证闭环NCS稳定,而且满足H∞性能指标. 数值仿真验证了方法的有效性.
| [1] | Antsaklis P, Baillieul J. Guest editorial for special issue on networked control systems[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1421-1423. |
| [2] | Gupta R A, Chow M Y. Networked control system: Overview and research trends[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2527-2535. |
| [3] | 霍志红, 方华京. 一类随机时延网络化控制系统的容错控制研究[J]. 信息与控制, 2008, 35(5): 584-587. Huo Z H, Fang H J. Fault-tolerant control of networked control systems with random time-delays[J]. Information and Control, 2008, 35(5): 584-587. |
| [4] | 郑英, 方华京. 具有随机时延的网络化控制系统基于等价空间的故障诊断[J]. 信息与控制, 2003, 32(2): 155-159. Zheng Y, Fang H J. Parity space based fault diagnosis of networked control systems with random delay[J]. Information and Control, 2003, 32(2): 155-159. |
| [5] | Li J G, Yuan J Q, Lu J G. Observer-based H∞ control for networked nonlinear systems with random packet losses[J]. IEEE Transactions on Automatic Control, 2010, 41(1): 39-46. |
| [6] | Zhang W A, Li Y. A robust control approach to stabilization of networked control systems with short time-varying delays[J]. IEEE Transactions on Automatic Control, 2010, 36(1): 87-91. |
| [7] | 孙业国. 时延丢包网络控制系统的分析与控制[J]. 计算机工程与应用, 2012, 48(21): 89-93. Sun Y G. Analysis and control of networked control systems with both time delay and packet dropout [J]. Computer Engineering and Applications, 2012, 48(21): 89-93. |
| [8] | Tian E G, Yue D. A new state feedback H∞ control of networked control systems with time-varying network conditions[J]. Journal of the Franklin Institute, 2012, 349(3): 891-914. |
| [9] | Zhu J W, Li Y P, Che W W. Non-fragile H∞ control for networked control system with quantization and time-delays[C]//Proceedings of the Chinese Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2011: 4276-4280. |
| [10] | Su Z Z, Yan H C, Zhang H. Quantized H∞ control for networked control systems with multiple packet dropouts[C]//Proceedings of the Chinese Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2012: 545-551. |
| [11] | Che W W, Wang J L, Yang G H. Quantized H∞control for networked control systems with packet dropouts[C]//Proceedings of the Chinese Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2009: 4087-4092. |
| [12] | Chong J. Quantized control for networked control systems with communication delay and packet dropouts[C]//Proceedings of the Chinese Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2014: 1989-1994. |
| [13] | 姚成法, 侯明善, 杨常伟. LMI方法非脆弱鲁棒H∞控制器设计[J]. 电光与控制, 2007, 14(6): 85-87. Yao C F, Hou M S, Yang C W. Non-fragile H∞ controller design based on LMI approach[J]. Electronics Optics and Control, 2007, 14(6): 85-87. |
| [14] | 曹慧超, 李炜. 执行器饱和不确定NCS非脆弱鲁棒容错控制[J]. 控制与决策, 2013, 28(12): 1874-1883. Cao H C, Li W. Non-fragile robust fault-tolerant control for uncertain NCS with actuator saturation[J]. Control and Decision, 2013, 28(12): 1874-1883. |
| [15] | 孙文安, 孙风杰, 裴炳南. 一类不确定时延网络控制系统的非脆弱H∞保成本控制[J]. 电机与控制学报, 2010, 14(2): 53-59. Sun W A, Sun F J, Pei B N. Non-fragile H∞ guaranteed cost control for a class of networked control systems with uncertain time delay[J]. Electric Machines and Control, 2010, 14(2): 53-59. |
| [16] | 于水情, 李俊明. 变采样周期网络控制系统的非脆弱保性能控制[J]. 系统工程与电子技术, 2011, 33(4): 856-861. Yu S Q, Li J M. Non-fragile guaranteed cost control for networked control systems under variable-period sampling[J]. Systems Engineering and Electronics, 2011, 33(4): 856-861. |
| [17] | Zhang H K, Fang Q S, Wang X L, et al. Non-fragile guaranteed-cost robust control for a class of nonlinear networked control systems with long time-delay [C]//Proceedings of International Conference on Intelligent Computation Technology and Automation. Piscataway, NJ, USA: IEEE, 2010: 784-787. |
| [18] | Li J G, Yuan J Q, Lu J G. Observer-based H∞ control for networked nonlinear systems with random packet losses[J]. IEEE Transactions on Automatic Control, 2010, 41(1): 39-46. |
| [19] | Rasool F, Nguang S K, Krug M. Robust H∞ output feedback control of networked control systems with multiple quantizers[C]//Proceedings of Industrial Electronics and Applications. Piscataway, NJ, USA: IEEE, 2011: 1541-1546. |
| [20] | Wang Z D, Yang F W. Robust H∞ control for networked systems with random packet losses[J]. IEEE Transactions on Automatic Control, 2007, 37(4): 916-922. |



