1 引言

在生活中到处都存在着复杂网络，如互联网、 电力网络、 交通运输网络、 大规模集成电路、 商业网络、 社会关系网等^[1-3]. 而通过观察可以看到，在不少实际的复杂网络中，它们的节点并不完全相同^[3]. 为了更好地了解实际生活中的复杂网络所呈现出来的动力学特征，对具有不同节点的网络进行研究就显得尤其重要.

近几十年来随着人们在耦合复杂网络上的研究不断深入，有关人工神经网络的稳定性和同步分析吸引了学者们的关注^{[4-12, 13]}. 如文^[4]给出了变时滞神经网络的指数稳定的条件，文^[10]对具有相同节点动态和不同拓扑结构的两个复杂网络间的同步进行了研究.

其中有限时间同步问题也得到了很广泛的研究^[14-24]. 文^[14]则对两个不同的带有不恒等节点的复杂网络的广义函数投影同步进行研究. 基于Barbalat引理，应用非线性反馈控制，推导出了系统同步的充分条件，其中复杂网络的节点没有限制局部线性. 而文^[17]研究了滞后型微分方程的有限时间稳定性和镇定性. 其中通过微分方程理论，利用李亚普诺夫函数得到有限时间稳定. 使用Artstein模型化简方法对非线性反馈控制时滞进行处理得到线性系统的有限时间镇定. 另外，驱动网络和响应网络节点不同维的不确定的复杂动力网络的广义函数矩阵投影滞后同步在文^[19]通过自适应的控制方法进行了研究. 基于李亚普诺夫稳定性理论，得到自适应控制器，驱动网络和响应网络的未知参数通过自适应法则进行了估计. 文^[20]给出自适应律和有限时间控制的概念，基于此提出构建自适应滑模控制器，确保系统在给定的有限时间按照预定“滑动模态”的状态轨迹运动，对两个不同的具有完全未知参数的混沌系统的有限时间混沌同步问题进行了研究.

然而，这些已经得到的成果的共同特点是有限时间同步中无论是驱动系统还是响应系统，它们里面单个网络的

维数都是一样的，即这里驱动系统和响应系统都是分别由相同维数的网络耦合而成的. 动态神经网络有限时间同步的驱动系统和响应系统里面的各个网络维数不一样时，文献提出的稳定或者同步控制器的设计将有所区别. 此时，针对这种动态神经网络的有限时间同步是值得讨论的问题.

综合以上分析，本文将对动态神经网络的有限时间同步进行研究，其中驱动系统和响应系统都是分别由不同维数的网络耦合而成的，即各系统中单个网络中节点数量不尽相同. 然后给出不同维数的神经网络系统的有限时间同步的充分条件.

2 复杂网络模型描述

本文首先介绍一些需要用到的数学符号.

A^T(或者x^T)表示矩阵A或者向量x的转置. ‖x‖表示向量x的二范数.

本文对以下耦合神经网络进行分析，并把它作为驱动系统：

其中，i=1，2，…，N，x_i=(x_i1，x_i2，…，x_ini)^T∈R^n_i表示第i个神经网络的神经元的状态向量. A_i，Φ_i∈R^n_i×n_i是常数矩阵，P_ij∈R^n_i×n_j是内部耦合矩阵，i，j=1，2，…，N. C=(c_ij)_N×N是表示系统的耦合强度和网络拓扑结构的外部耦合矩阵.

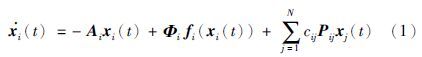
把式(1)作为驱动系统，然后相对应的一个带有非线性控制器的响应系统如下：

其中，i=1，2，…，N，y_i=(y_i1，y_i2，…，y_imi)^T∈R^m_i表示系统中第i个神经网络的神经元的状态向量. B_i，Ψ_i∈R^m_i×m_i，Q_ij∈R^m_i×m_j，D=(d_ij)_N×N的定义和A_i，Φ_i∈R^n_i×n_i、 P_ij∈R^n_i×n_j、 C=(c_ij)_N×N一样. u_i(t)=(u_i1，u_i2，…，u_imi)^T∈R^m_i是一个非线性的反馈控制器.

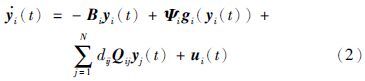
这里驱动系统和响应系统都是分别由不同维数的网络耦合而成的.

定义1  x_i(t-τ(t))表示驱动系统中第i个神经网络的神经元的时滞状态向量，τ(t)≥0是指变化时滞函数，y_i(t)表示响应系统中第i个神经网络的神经元的当前状态向量，M_i=(m_ij)_mi×ni为缩放函数矩阵. 如果存在有限时间T_f>0，使得

则可以得到系统(1)和(2)达到有限时间同步.

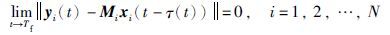
假设1  激励函数g_i(y_i)=(g_i1(y_i1)，g_i2(y_i2)，…，g_imi(y_imi))^T是利普希茨连续，即存在β_ik>0，使得

其中，ξ₁，ξ₂∈R，i=1，2，…，N，l=1，2，…，n_i，k=1，2，…，m_i.

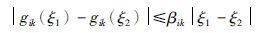
假设2  变化时滞函数τ(t)满足： 对于所有t，0≤τ(t)<h，(t)<δ<1.

引理1  对于任意x，y∈Rⁿ和正定矩阵Q∈R^n×n，以下不等式成立：

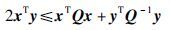
引理2 ^[24] 假设存在正定连续可微的函数V(t)满足${\dot{V}}$(t)≤-αV^η(t)，常数α>0，0<η<1，那么对于任意t₀，V(t)满足以下不等式：

且V(t)≡0，t≥T_f，.

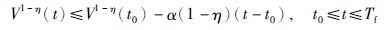
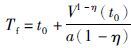引理3  设a₁，a₂，…，a_n>0，0<r<p，则

3 同步条件分析

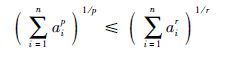
定义同步误差为e_i(t)=y_i(t)-M_ix_i(t-τ(t))，i=1，2，…，N，M_i是一个非零矩阵，M_i∈R^m_i×n_i，则e_i(t)∈R^m_i关于时间t的导数为

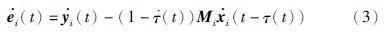
把式(1)和式(2)代入式(3)，得

定理1  在满足假设1、 2的条件下，对于给定的非零缩放矩阵M_i，当非线性控制器如下定义：

其中，i=1，2，…，N，α>0，0<η<1，若存在足够大的k_i，K=diag(k₁·I_m1，k₂·I_m2，…，k_N·I_mN)，使得 则驱动系统(1)和响应系统(2)可以达到有限时间同步. E为单位对角矩阵， β_i=diag(β_i1，β_i2，…，β_imi)， β=diag(β₁，β₂，…，β_N)，B=diag(B₁，B₂，…，B_N)， Ψ=diag(Ψ₁，Ψ₂，…，Ψ_N)， H=

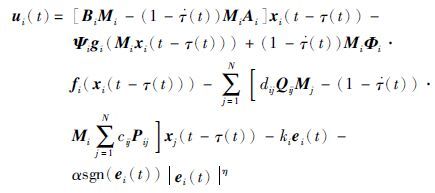
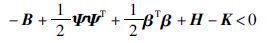
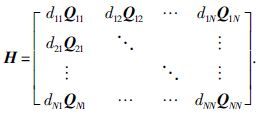
证明  令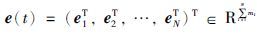，取李亚普诺夫函数V(t)=$\frac{1}{2}$e^T(t)e(t).

由引理1得 所以

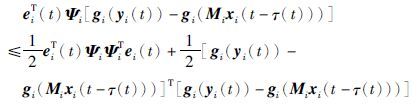
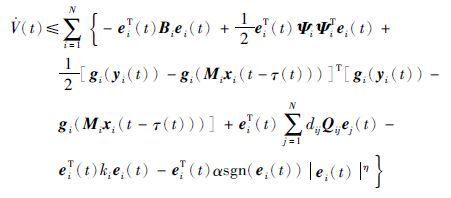
由假设1中激励函数的性质可知

所以 即

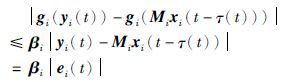
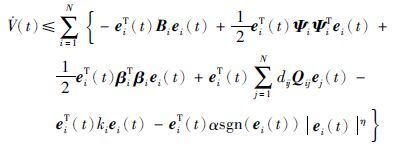
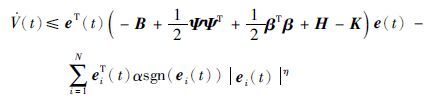
因为-B+$\frac{1}{2}$ΨΨT+$\frac{1}{2}$β^Tβ+H-K<0，所以${\dot{V}}$(t)≤0，因此V·(t)是负定的.

又因为

由引理3，可得： 所以

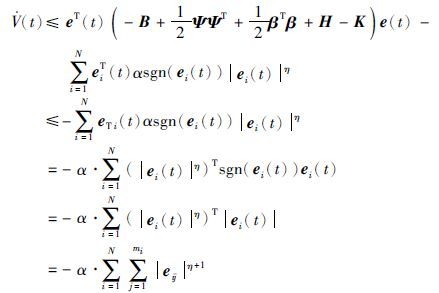
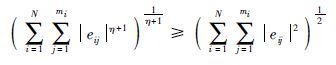
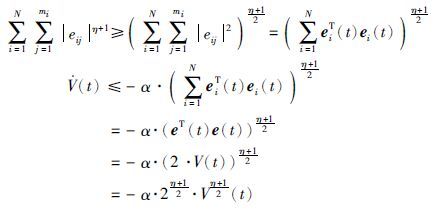
由引理2得到驱动系统(1)和响应系统(2)可以达到有限时间同步，即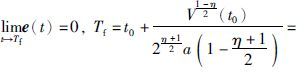

4 数据仿真

本节举出2个例子来证明以上定理1的有效性.

例子1  考虑驱动系统(1)和响应系统(2)分别由5个神经网络组成. 其中驱动系统为

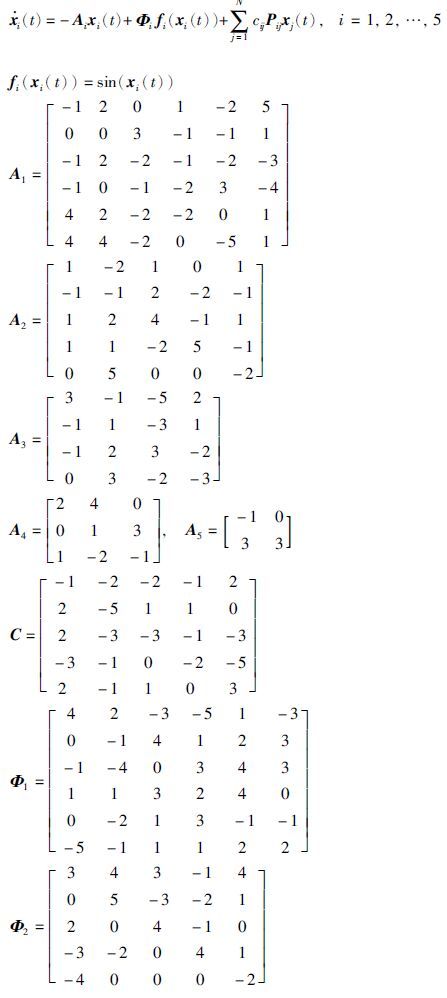
对应的响应系统为

其中，i=1，2，…，5，g_i(y_i(t))=cos(y_i(t))，可取β_i为单位矩阵. 取α=2，η=0.5.

同步误差：

其中，

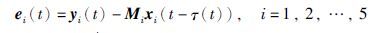
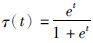
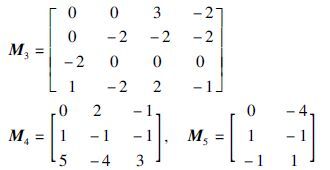
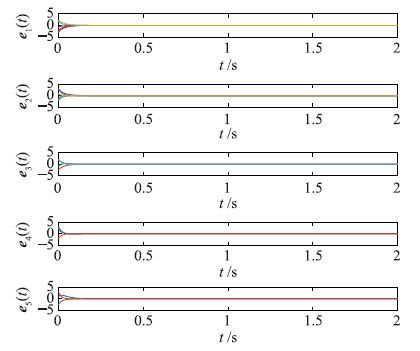
令k₁=46，k₂=43，k₃=40，k₄=36，k₅=35，经过计算验证-B+$\frac{1}{2}$ΨΨT+$\frac{1}{2}$β^Tβ+H-K<0，得到如图 1所示的同步误差的演化曲线. 驱动系统(1)和响应系统(2)可以达到有限时间同步，T_f=3.83 s.

例子2  考虑驱动系统(1)和响应系统(2)分别由3个神经网络组成. 驱动系统为

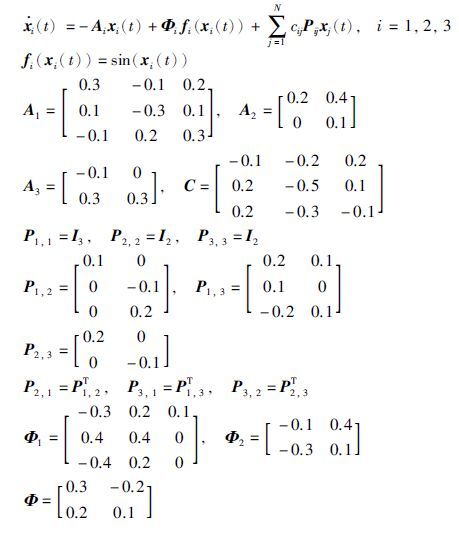
响应系统为<

其中，i=1，2，3，g_i(y_i(t))=cos(y_i(t))，同样的取β_i为单位矩阵. 在控制器u_i(t)中，参数α=3，η=0.6.

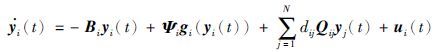
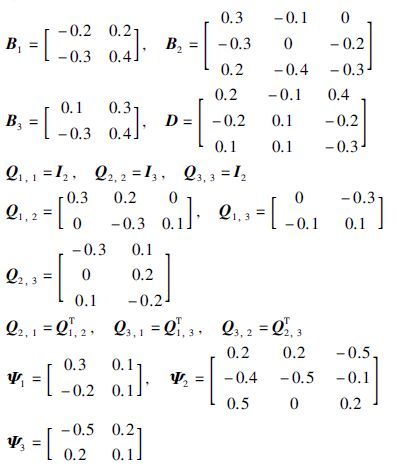
同步误差：

其中，

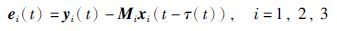
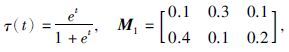
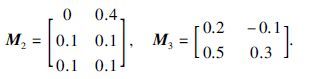
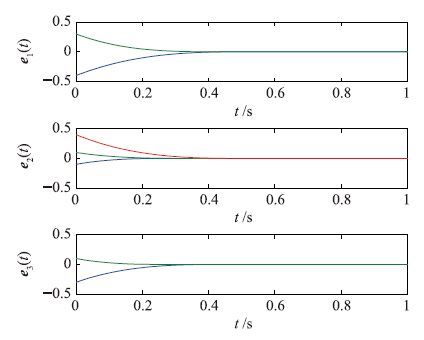
取k₁=1.75，k₂=1.94，k₃=1.4，经计算验证可得-B+$\frac{1}{2}$ΨΨT+$\frac{1}{2}$β^Tβ+H-K<0，得到如图 2所示结果. 当T_f=0.84 s，驱动系统(1)和响应系统(2)可以达到有限时间同步.

5 结论

本文对驱动系统和响应系统都是分别由不同维数的网络耦合而成的动态神经网络的有限时间同步进行了研究. 在驱动系统和响应系统中单个网络中节点数量不尽相同的情况下，设计非线性反馈控制器，以此为条件给出不同维数的神经网络系统的有限时间同步的一些充分条件. 另外，着力于设置简单的反馈控制器，克服控制器复杂以至于在实际情况中难以应用的问题，这是往后一个重点的研究方向.