2. 宁波大学信息科学与工程学院, 浙江 宁波 315211;
3. 河海大学物联网工程学院, 江苏 常州 213022
2. Faculty of Electrial Engineering and Computer Science, Ningbo University, Ningbo 315211, China;
3. College of Internet of Things Engineering, HoHai University, Changzhou 213022, China
由于机械臂在自动化生产过程中的重要作用,近年来对机械臂的控制问题成为了研究的热点. 其中,关于机械臂的轨迹跟踪问题的研究尤其活跃[1-2]. 机械臂的轨迹跟踪控制广泛采用计算力矩的方法[3]. 但是随着对跟踪精度和速度等要求的提高,就不得不考虑摩擦和扰动等不确定性因素. 这也给计算力矩的控制方法,带来了新的挑战. 而处理这些不确定因素的一个比较好的方法是对其进行逼近,然后进行补偿. 基于此思路,神经网络的非线性逼近能力可用于实现对机械臂的不确定性的补偿[4-7]; 神经网络理论比较成熟,但是难以应用一些已知的信息和相关经验来设计控制系统. 席雷平等人利用非线性干扰观测器,来处理机械臂存在的不确定干扰[8]. 尽管这种方案提高了机械臂关节的跟踪精度,但非线性干扰观测器设计要求干扰的变化是十分缓慢的. 廖武等人给出了一种鲁棒补偿器,来实现对不确定性的补偿[9]. 这种方法能够起到不错的效果,但是鲁棒补偿器的参数选择过于繁难. 文[10-16]利用模糊系统的万能逼近特性来实现对不确定性的逼近,然后进行相应的补偿处理,并为模糊系统设计了相应的自适应律. 模糊补偿方案是目前应对不确定性的较好的方法,但为了保证逼近精度,必须使用更多的模糊规则,目前研究的自适应模糊系统普遍存在维数较高的问题. 文[17]所构造的自适应律采用鲁棒控制的方法克服不确定性带来的影响,该控制器的鲁棒性较强,但是鲁棒控制是一种十分保守的控制器,其稳定性在大多数情况下是以牺牲动态性能来保障的.
本文针对具有不确定性的机械臂,提出一种基于计算力矩与不确定性补偿的自适应控制方案. 针对机械臂的标称部分,直接采用计算力矩的方法设计出相应的控制量. 对于机械臂的不确定性摩擦,则构造相应的模糊系统进行逼近. 考虑到机械臂存在的扰动为时变的有界变量,因此可针对扰动设计一个附加的反馈控制量,以克服其带来的影响. 为保证控制系统的稳定性,均基于李亚普诺夫稳定性理论选择所用的控制律.
2 问题描述针对任意一个n关节的机械臂,在理想情况下(无摩擦和扰动),其模型如下所示[18]:
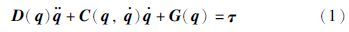
实际中机械臂一般还会存在摩擦和扰动等不确定因素,因而机械臂模型可表示为[13]
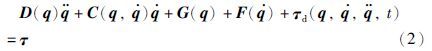
针对理想模型(1),通常可以利用计算力矩的方法设计控制
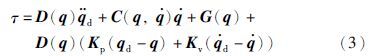

然而机械臂系统具有强耦合、 高度非线性的特点,尤其是当系统参数不确定时,控制系统的设计变得更加困难. 此时利用标称的计算力矩法所设计的机械臂控制系统很难得到令人满意的结果. 例如,对于实际模型(2),由于包含了摩擦F(${\dot{q}}$)和扰动τd(q,,${\ddot{q}}$,t)等不确定因素,所以显然不能直接运用计算力矩的方法得到合适的控制律.
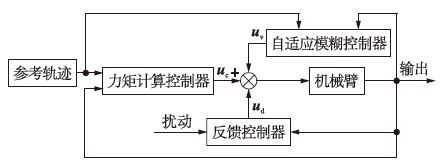
3 基于自适应模糊算法的控制系统设计对于任意一个非线性连续函数f(x)(x∈Rn),根据模糊系统的万能逼近特性,总可以根据一定的模糊规则来构造相应的模糊系统逼近f(x),实现非线性补偿的目的. 实际应用的机械臂,由于其结构的复杂性,常常存在建模误差,主要为不确定摩擦和扰动. 假设摩擦和扰动在实际中以未知力矩的形式施加于机械臂. 本文构造的复合控制系统,首先针对机械臂普遍存在的摩擦,构造自适应模糊系统逼近摩擦,从而得到摩擦部分的补偿控制量; 对于实际存在的随机扰动,设计反馈控制律,以克服扰动带来的影响; 最后将这两者与计算力矩的控制方法相结合,实现对期望轨迹的跟踪控制. 该复合控制系统的结构如图 1所示.
|
| 图 1 基于自适应模糊控制的机械臂复合控制框图 Fig. 1 Configuration of compound control of manipulator based on adaptive fuzzy controller |
首先,针对机械臂关节j(j=1,2,…,n)的摩擦Fj(${\dot{q}}$j)∈R设计Mj条模糊规则<
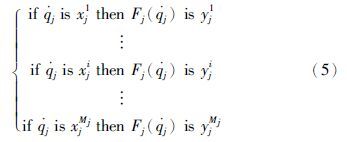
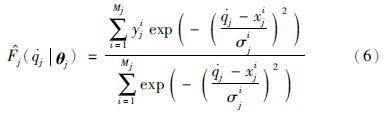
定义模糊系统的最优参数集合为
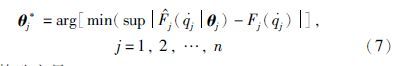
构造变量

令${\tilde{\theta }}$j=θj-θ*j,其中Λ∈Rn×n,其特征值均大于0. 构造李亚普诺夫函数
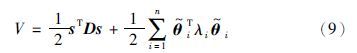
将式(9)对时间求导,可得
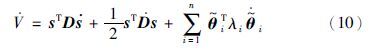
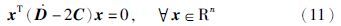
令x=s,根据式(2)、 式(8)和式(11),令${\dot{q}}$t=${\dot{q}}$d-Λ${\tilde{q}}$,可将式(10)进一步写为
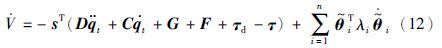
通常时变干扰τd是有界的,有
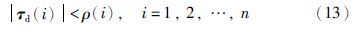
令${\hat{F}}$=(${\hat{F}}$1(${\dot{q}}$1θ1),${\hat{F}}$2(${\dot{q}}$2θ2)…,${\hat{F}}$n(${\dot{q}}$nθn))T,并设计控制律
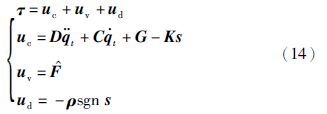
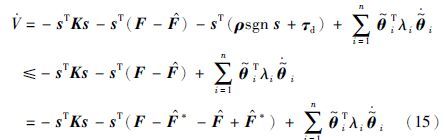
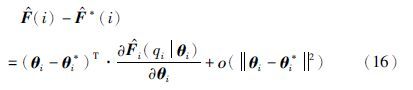
令w(i)=F(i)-${\hat{F}}$(i)+ο(θi-θ*i2),其中ο(‖θi-θ*i2‖)为‖θi-θ*i2‖的高阶无穷小量. 则式(15)可改写为
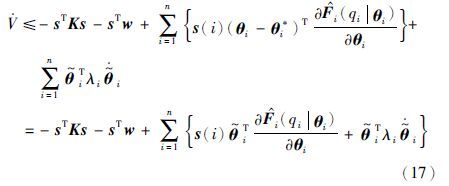
取自适应律
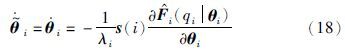
式(17)可化简为

显然-sTKs<0,$\forall $s≠0,所以在最优逼近误差足够小的情况下有

模糊系统具有万能逼近特性,而自适应律能够保证模糊系统在不同时刻适用于整个状态空间的不同区域,所以条件(20)能够得到满足,因此使得${\dot{V}}$<0. 所以控制律(14)和自适应律(18)能够保证闭环系统的稳定性.
值得注意的是控制量ud由于采用了符号函数对控制量进行切换,因而在实际控制中可能会存在颤抖现象. 此时可以利用陡峭的饱和函数加以改进
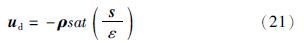
只要ε选得合适(通常在10-3~10-4选取),则可以使得原不连续控制器(14)变为连续的控制器,从而消除颤抖现象.
3.3 自适应律的实现
自适应律(18)中含有偏导数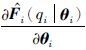 的计算,这可以利用复合函数的求导法则,来实现对
的计算,这可以利用复合函数的求导法则,来实现对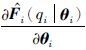 的计算,具体方法如下:
的计算,具体方法如下:
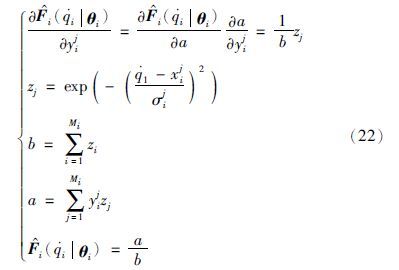
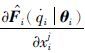 可以按照式(23)计算
可以按照式(23)计算
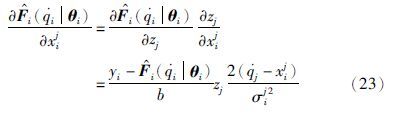
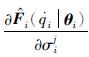 可按式(24)计算
可按式(24)计算
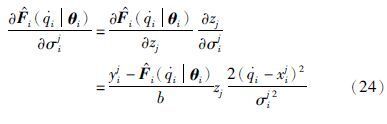
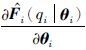 可由式(22)、 (23)和(24)来计算得到.
4 仿真结果及其分析
可由式(22)、 (23)和(24)来计算得到.
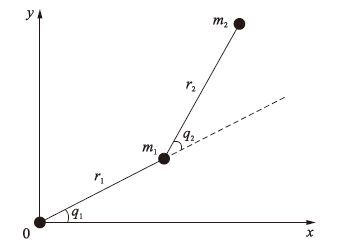
4 仿真结果及其分析为简单起见,不失一般性,机械臂选择为双关节,其简化图如图 2所示. 其中,r1为机械臂大臂的臂长,r2为机械臂小臂的臂长,m1为大臂的质量,m2为小臂的质量. 其数学模型具体如式(25)所示[13].
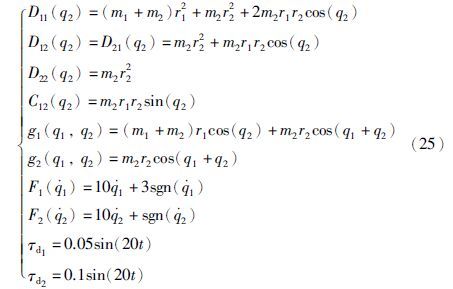
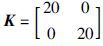 针对扰动ρ=diag(0.05,0.1)、 依据式(14)确定控制律,
针对扰动ρ=diag(0.05,0.1)、 依据式(14)确定控制律,
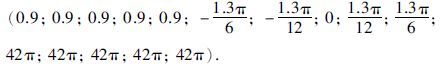
|
| 图 2 双关节机械臂的简化图 Fig. 2 The simplified graphic of dual-joint manipulator |
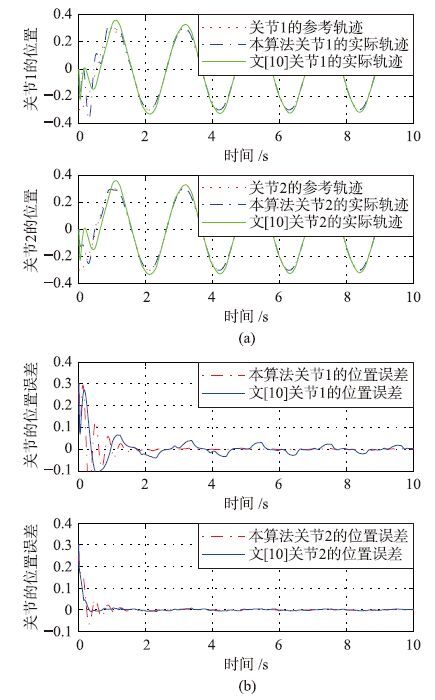
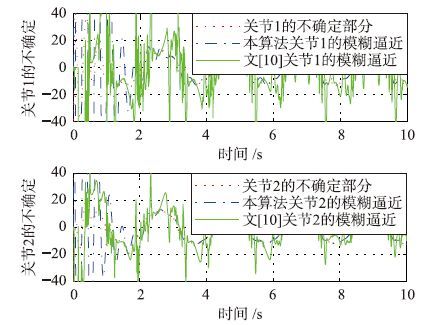
本文将上述自适应模糊控制率用于该模型,并与文[13]所提出的算法进行比较. 跟踪正弦信号的效果如图 3(a)和图 3(b)所示,其中图 3(a)为跟踪情况的比较,图 3(b)为跟踪误差. 图 4是模糊系统对不确定摩擦逼近的情况.
|
| 图 3 两种算法下对正弦信号的轨迹跟踪 Fig. 3 Trajectory tracking of sine signal with two algorithms |
|
| 图 4 对正弦信号进行轨迹跟踪时对不确定信息的逼近 Fig. 4 The approximating of uncertain information in trajectory tracking of sine signal |
由图 3(a)可以看出,两种算法都能实现对正弦信号的轨迹跟踪,但是从图 3(b)可以看出本文算法在1.5 s之后,机械臂关节1的跟踪误差几乎为0,而文[13]的算法始终存在一定的跟踪误差. 对比发现,本文所提出算法跟踪精度更高.
图 4是模糊系统对不确定信息逼近的情况. 从图 4可以看出,采用本文提出的自适应律实现了对不确定性摩擦更好的逼近.
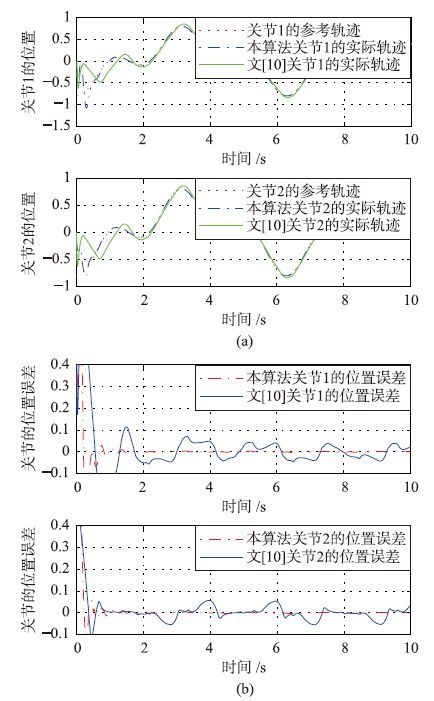
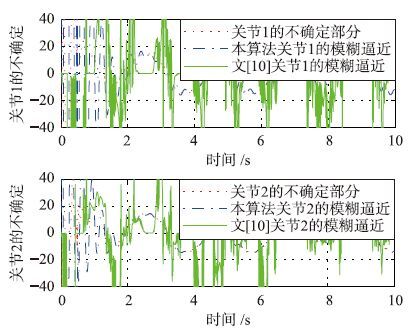
跟踪不规则给定信号的效果如图 5所示,其中5(a)为跟踪情况,5(b)为跟踪误差. 跟踪不规则信号时,模糊系统对不确定信息的逼近效果如图 6. 从图 5和图 6再次验证本文算法使得机械臂对给定轨迹具有更高的跟踪精度,对不确定性摩擦的逼近精度跟高.
|
| 图 5 两种算法下对不规则信号的轨迹跟踪 Fig. 5 Trajectory tracking of irregular signal with two algorithms |
|
| 图 6 对不规则信号进行轨迹跟踪时对不确定信息的逼近 Fig. 6 The approximating of uncertain information in trajectory tracking of irregular signal |
针对刚性机械臂存在摩擦和扰动等不确定因素给轨迹跟踪控制带来的困难,基于李亚普诺夫稳定性理论,给出了一种机械臂的自适应模糊复合控制策略. 该策略针对机械臂的确定部分设计了相应的控制量,并构造模糊系统逼近摩擦,得到一个补偿控制量,同时利用扰动的有界性设计反馈控制律,以克服扰动带来的影响. 本文设计的基于摩擦以及扰动的自适应律能够保证构造的李亚普诺夫函数的导数负定,因而控制系统的稳定性能能够得到保证. 仿真结果表明,该算法能够显著提高跟踪精度,同时能够很好地在保证模糊系统对不确定性的逼近精度的同时,保证控制器稳定.
| [1] | Yang H, Yu Y, Yuan Y, et al. Back-stepping control of two-link flexible manipulator based on an extended state observer[J]. Advances in Space Research, 2015, 56(10): 2312-2322. |
| [2] | 杜佩君, 张瑞锋. 基于增广ESN的机器人轨迹跟踪控制[J]. 信息与控制, 2013, 42(4): 443-448.Du P J, Zhang R F. Trajectory tracking control for robots based on Augmented ESN[J]. Information and Control, 2013, 42(4): 443-448. |
| [3] | 孙树栋. 工业机器人技术基础[M]. 西安: 西北工业大学出版社, 2006: 233-371. Sun S D. Technology base of industrial robots[M]. Xi′an: Northwestern Polytechnical University Press, 2006: 233-371. |
| [4] | Liu H, Zhang T. Adaptive neural network finite-time control for uncertain robotic manipulators[J]. Journal of Intelligent and Robotic Systems: Theory and Applications, 2014, 75(3): 363-377. |
| [5] | 刘建昌, 苗宇. 基于神经网络补偿的机械臂轨迹控制策略的研究[J]. 控制与决策, 2005, 20(7): 732-736. Liu J C, Miao Y. Research on trajectory control strategy of robot arm based on neural network compensation[J]. Control and Decision, 2005, 20(7): 732-736. |
| [6] | Zhu Q G, Chen Y, Wang H R. The RBF neural network control for the uncertain robotic manipulator[C]//Proceedings of the 2009 International Conference on Machine Learning and Cybernetics. Piscataway, NJ, USA: IEEE, 2009: 1266-1270. |
| [7] | 乃永强, 李军. 基于极限学习机的机械臂自适应神经控制 [J]. 信息与控制, 2015, 44(3): 257-262.Nai Y Q, Li J. Adaptive neural control of manipulators based on extreme learning machine[J]. Information and Control, 2015, 44(3): 257-262. |
| [8] | 席雷平, 陈自力, 齐晓慧. 基于非线性干扰观测器的机械臂自适应反演滑模控制[J]. 信息与控制, 2013, 42(4): 470-477. Xi L P, Chen Z L, Qi X H. Adaptive back stepping sliding mode control for robotic manipulator with nonlinear disturbance observer[J]. Information and Control, 2013, 42(4): 470-477. |
| [9] | 廖武, 钟宜生, 石宗英. 基于信号补偿的机械臂鲁棒控制器设计与实现[J]. 清华大学学报: 自然科学版, 2006, 46(4): 473-476. Liao W, Zhong Y S, Shi Z Y. Design and realization of robust manipulator controllers based on signal compensation[J]. Journal of Tsinghua University: Sciences & Technology, 2006, 46(4): 473-476. |
| [10] | Chen Y, Ma G, Lin S, et al. Adaptive fuzzy computed-torque control for robot manipulator with uncertain dynamics[J]. International Journal of Advanced Robotic Systems, 2012, 9(3): 1-9. |
| [11] | 倪骁骅, 刘青. 基于MIMO系统的机械手自适应模糊滑模控制[J]. 中国农机化学报, 2015(2): 265-268. Ni X H, Liu Q. Adaptive fuzzy sliding mode control for manipulator based on MIMO system[J]. Journal of Chinese Agricultural Mechanization, 2015, 36(2): 265-268. |
| [12] | 梁捷, 陈力. 空间机械臂关节运动的自适应模糊补偿控制[J]. 系统仿真学报, 2011, 23(3): 577-582. Liang J, Chen L. Fuzzy logic adaptive compensation control for space manipulator to track desired trajectory in joint space[J]. Journal of System Simulation, 2011, 23(3): 577-582. |
| [13] | Yoo B K, Ham W C. Adaptive control of robot manipulator using fuzzy compensator[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(2): 186-199. |
| [14] | Baghli F Z, bakkali L E, Lakhal Y. Multi-input multi-output fuzzy logic controller for complex system: Application on two-links manipulator[J]. Procedia Technology, 2015, 19: 607-614. |
| [15] | Al-Dabbagh R D, Kinsheel A, Mekhilef S, et al. System identification and control of robot manipulator based on fuzzy adaptive differential evolution algorithm [J]. Advances in Engineering Software, 2014, 78: 60-66. |
| [16] | Ghosh B B, Sarkar B K, Saha R. Realtime performance analysis of different combinations of fuzzy-PID and bias controllers for a two degree of freedom electrohydraulic parallel manipulator [J]. Robotics and Computer-Integrated Manufacturing, 2015, 34: 62-69. |
| [17] | 于志刚, 沈永良, 宋中民. 机械臂鲁棒自适应运动控制[J]. 控制理论与应用, 2011, 28(7): 1021-1024. Yu Z G, Shen Y L, Song Z M. Robust adaptive motion control for manipulator[J]. Control Theory & Applications, 2011, 28(7): 1021-1024. |
| [18] | 郭益深, 陈力. 具有外部扰动的空间刚性机械臂姿态与末端爪手协调运动的Terminal滑模控制算法设计[J]. 应用数学和力学, 2008, 29(5): 525-532. Guo Y S, Chen L. Terminal sliding mode control for coordinated motion of space rigid manipulator with external disturbance[J]. Applied Mathematics and Mechanics, 2008, 29(5): 525-532. |
| [19] | 刘强, 尔联洁, 刘金琨. 摩擦非线性环节的特性、 建模与控制补偿综述[J]. 系统工程与电子技术, 2002, 24(11): 45-52. Liu Q, Er L J, Liu J K, Overview of characteristics, modeling and compensation of nonlinear friction in servo systems[J]. Systems Engineering and Electronics, 2002, 24(11): 45-52. |



