作为空间机器人执行在轨服务任务的前提,自由漂浮空间机器人(free floating space robot,FFSR)的规划与控制问题已成为当今空间机器人领域的研究热点[1-2]. 然而,在任务空间的规划和跟踪控制过程中,不可避免地会遇到动力学奇异问题,使得机械臂末端不按预期轨迹运动[3],同时也会导致相应的控制方法失效. 因此,采用相应的奇异回避方法规划出期望的机械臂末端轨迹是非常有意义的.
目前使用的FFSR奇异回避路径规划方法主要有三类: 其一是奇异点消除法[4-5],即在动力学奇异点采取叠加等方法,牺牲部分精度消除雅可比矩阵奇异的影响,从而解决笛卡尔路径规划中的动力学奇异问题. 其二是奇异问题转化法[6-7],即将动力学奇异问题转化成其它便于分析计算的问题,从而避免直接求解逆广义雅可比矩阵. 其三是回避奇异点规划法[8-9],根据FFSR在其路径相关空间(path dependent workspace,PDW)内的动力学奇异特性,规划出能回避动力学奇异点的末端运动轨迹. 相比前两种方法而言,该类方法无需改变系统的广义雅可比矩阵,运算量小且不影响所有方向精度.
奇异回避算法虽保证了运动过程中广义雅可比矩阵的可逆性,但由于在空间机械臂轨迹跟踪过程中存在初始误差与冲击响应的干扰,往往导致机械臂无法完全按照规划完成任务. 因此,合适的跟踪控制器设计也显得尤为重要. 状态依赖Riccati方程(state-dependent Riccati equation,SDRE)方法作为一种非线性准最优/次优化控制的重要方法[10],可以实现对机械臂轨迹的跟踪控制[11-14]. 然而,大多基于SDRE的设计针对的是地面机械臂,并未涉及到基座与臂杆存在动力学耦合关系的FFSR控制问题.
针对FFSR机械臂末端在任务空间内运动的情况,本文提出了一种避奇异规划—跟踪算法,在实现对末端速度轨迹精确跟踪的同时,还克服了传统方法将轨迹约束在路径无关空间(PIW)导致工作空间利用率降低的缺点. 利用回避奇异点规划法计算避奇异阈值并生成回避动力学奇异的末端运动轨迹,保证广义雅可比矩阵的可逆性. 进一步,基于SDRE方法设计优化控制律,保证了闭环系统局部渐近稳定,使FFSR可以快速跟踪参考轨迹并准确运行至目标点. 最后,通过实例仿真验证了算法的有效性.
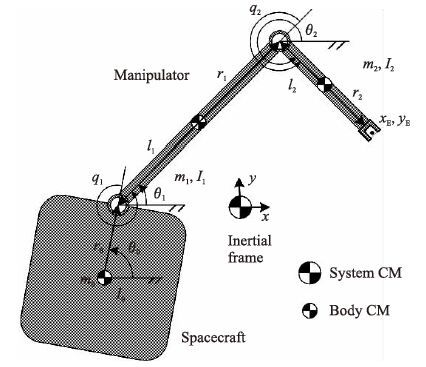
2 问题提出 2.1 自由漂浮空间机器人模型本文选取二连杆自由漂浮空间机器人为研究对象. 该系统由自由漂浮基座B0和连杆B1、 B2组成,机械臂与航天器基座只能在垂直于关节角旋转轴的平面内运动,如图 1所示.
|
| 图 1 二连杆自由漂浮空间机器人系统 Fig. 1 Two-link FFSR system model |
为了使问题简明起见,做如下假设:
(1) 系统不受任何外力及外力矩的作用,因此运动过程中系统满足动量守恒定律.
(2) 系统的每个杆件均为刚体,相邻杆件间的关节具有一个可主动控制的旋转自由度,但载体处于漂浮状态即基座位姿不受控.
(3) 系统基座初始角速度为0,初始角动量为0.
(4) 系统模型参数精确.
将整个系统的质心作为惯性坐标系原点,那么机械臂末端在惯性坐标中的位置可表示为[8, 15]
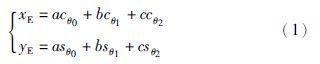
忽略重力引起的力矩向量,简化拉格朗日方程可导出自由漂浮空间机器人系统的动力学方程[16]:
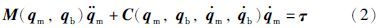
自由漂浮空间机器人广义雅可比矩阵不仅与系统各部分的几何参数有关,还与质量、 转动惯量的分布有关,因此存在动力学奇异问题. 对于文中研究的二连杆平面自由漂浮空间机器人,采用下述方法对其动力学奇异性进行分析.
假设系统初始角动量为0,那么运动过程中满足角动量守恒方程[8, 17]:
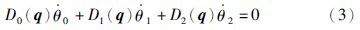
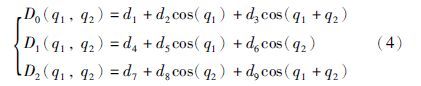
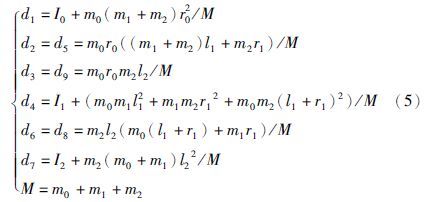
由式(1)可以得到机械臂末端的线速度表达式,结合角动量守恒方程,那么有:

由式(6)可以看出,当S(q1,q2)=0时系统发生动力学奇异,其具体表达式满足[9]:
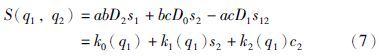
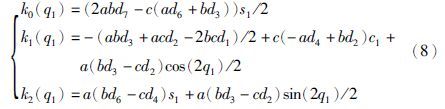
分别令Smin,Smax为函数S(q1,q2)的上下界,对于每一个S=S*(S*∈[Smin,Smax])都满足下述关节角关系:
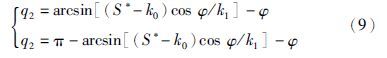

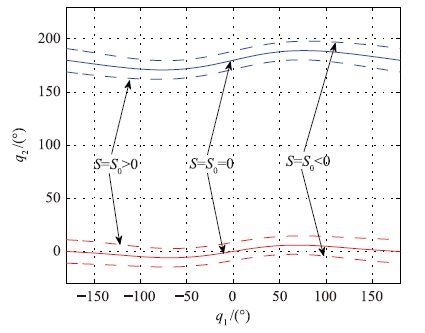
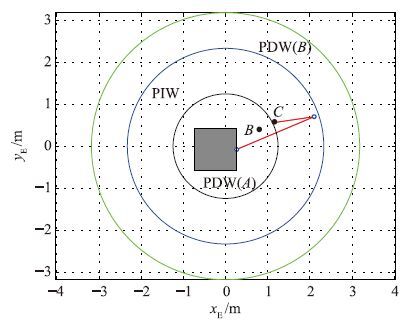
令S*=0,q1,q2∈[-π,π],在关节空间得到系统奇异解的集合,称之为奇异线,如图 2实线所示. 将关节空间的奇异解通过式(1)映射到任务空间,分别对应路径相关工作空间PDW(B)和PDW(A),如图 3所示. 系统可达工作空间减去PDW得到路径无关工作空间PIW. 当机械臂末端在PIW中运动时,不会发生动力学奇异问题. 但这类问题可能会发生在末端在PDW内运动的情况下,这不仅取决于系统的初始位姿,还与机械臂的运动路径有关. 图 2、 图 3中所用参数如仿真实验部分表 1所示(第4小节).
|
| 图 2 二连杆FFSR的奇异线和边界线 Fig. 2 Singularity and margin curves of two-link FFSR |
|
| 图 3 二连杆FFSR的PIW和PDW区域 Fig. 3 Path independent workspace (PIW) and path dependent workspace (PDW) for a two-link free floating space robot |
基于上述对二连杆自由漂浮空间机器人奇异性的分析,在进行任务空间跟踪控制时,学者们通常假设规划出的轨迹全部位于工作空间内的PIW区域中[18],从而避免跟踪过程中动力学奇异问题的发生. 然而PIW区域非常有限,实际过程中将规划轨迹约束在PIW区域势必导致其实际工作空间的减少,因此自由漂浮空间机器人机械臂末端在PDW区域中的避奇异轨迹规划跟踪是具有实际意义的.
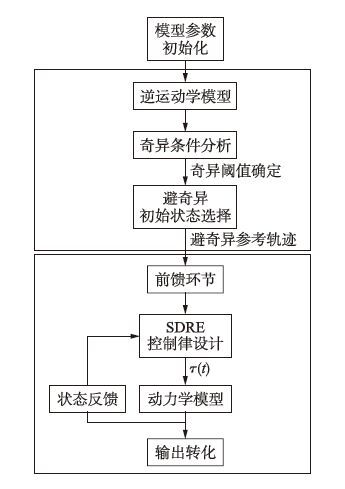
3 避奇异规划—跟踪算法为了实现机械臂在PDW区域内运动时快速稳定地运行至目标点,本文提出一种避奇异规划—跟踪算法,算法流程如图 4所示. 首先根据二连杆FFSR运动模型及相应的奇异条件约束,结合预定末端轨迹,计算出不发生奇异的初始关节角及基座姿态角参数值,为跟踪控制器规划出不发生动力学奇异的末端运动轨迹及初始状态值. 然后基于状态依赖Riccati方程设计SDRE控制律,实现对末端参考轨迹的准确跟踪,保证了闭环系统的局部渐近稳定性. 规划及跟踪算法虽分别设计但构成整体,保证机械臂末端PDW区域内准确稳定地运行至目标点.
|
| 图 4 FFSR避奇异规划—跟踪算法流程图 Fig. 4 The flow-chart of trajectory planning and tracking algorithm for FFSR |
由前文奇异性分析可知,当机械臂末端在任务空间沿着某一个轨迹运动时,其关节角也必定沿着q2-q1空间内的对应曲线运动,一旦关节运动曲线与奇异线相交或相切,机械臂运动将发生动力学奇异.
规划机械臂末端沿CB做直线运动,其中点C为初始点,位于PIW与PDW区域的公共边界圆上; 点B位于PDW(A)内,如图 3所示. 文[8]指出,在末端轨迹确定的条件下,机械臂关节角的变化过程仅与系统的初始关节角及基座姿态角有关. 为了避免机械臂末端在PDW区域运动时奇异问题的发生,假设存在安全边界线S0∈[0,Smax],若满足系统末时刻的S(q1,q2)与安全边界线相交,且运动过程中S(q1,q2)在[S0,Smax]范围内变化,则整个运动过程将不会出现动力学奇异. 需要说明的是,上述为运动过程不发生奇异的一个充分条件. 通过求解满足上述条件的初始状态值(关节角及基座姿态角)来回避运动过程中动力学奇异的发生.
规划任务空间的末端轨迹在过原点直线上,其运动方程满足:
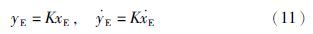

设期望的末端位移s(t)表达式为
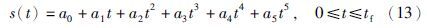
那么末端线速度可以简化表示为

由边界条件可以分别确定出位移表达式中的所有待定参数[19].
在t=tf时刻,系统基座姿态角及机械臂关节角与机械臂末端位置满足关系:
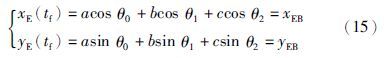

回避奇异点规划法通过计算避奇异阈值,为进一步完成跟踪控制规划出避奇异的参考轨迹并提供初始状态值. 相比于阻尼最小二乘法等避奇异方法来说,克服了其在回避奇异时牺牲末端部分精度的缺点.
3.2 基于SDRE的跟踪控制器当存在初始误差时,需要进行误差反馈控制,保证空间机器人从任意初始状态出发都能够跟随预先设定好的期望轨迹,从而完成系统的实际操作任务.
避奇异轨迹规划部分提供的参考轨迹及初始状态值回避了动力学奇异点,因此机械臂末端在PDW区域的运动过程中不会发生动力学奇异问题,整个系统广义雅可比矩阵可逆. 基于此,本节提出一种SDRE跟踪控制器实现对末端速度的跟踪控制.
定义二连杆自由漂浮空间机械臂状态变量为x=[x1 x2]T=[$\dot{q}$1 $\dot{q}$2]T. 容易证明式(2)中M是可逆的[18],那么系统的状态方程可以写成具有状态依赖参数的类线性结构形式:
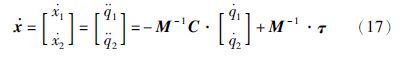
根据自由漂浮空间机器人关节角速度与机械臂末端速度的关系,可以将输出方程表述为

从系统状态方程中选取SDC矩阵为
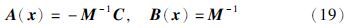
当满足如下条件时,非线性跟踪系统具有局部稳定、 局部渐近最优的SDRE控制律[20]:
(1) {A(x),B(x)}逐点可控;
(2) {A(x),Q1/2}逐点可观;
由于上述系统中惯性矩阵M正定,那么系统的能控性矩阵QC(x)={B(x)A(x)B(x)…An-1(x)B(x)}的秩满足rank{B(x)A(x)B(x)}=2,则在平衡点的邻域内{A(x),B(x)}逐点可控,因此二连杆自由漂浮空间机器人系统是可控的. 而系统的能观性则可通过选取Q>0保证,即{A(x),Q1/2}是逐点可观的. 因此闭环系统是局部渐近稳定的.
设计速度输出跟踪指标为
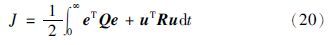
对于由非线性系统方程(17)及其性能指标函数(20)描述的无限时间状态调节问题,可以设计SDRE控制律为
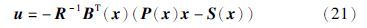
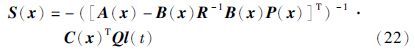
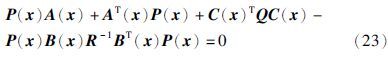
SDRE控制律使得非线性输出跟踪系统是局部渐近稳定的,这也说明SDRE只是一种次优控制而并非全局最优控制. 但是可以根据空间机械臂工作的实际需求,对系统的跟踪精度和控制量的大小进行有效地折中,得到兼顾精确性和稳定性的控制,体现出SDRE跟踪控制律设计的灵活性.
4 仿真实验与结果分析为了验证设计的规划—跟踪算法的有效性,对二连杆自由漂浮空间机器人系统在PDW区域内进行跟踪仿真.
表 1给出了系统仿真试验的结构参数和运动参数. 规划机械臂末端从点C=(1.113 3,0.556 7)运动到PDW区域内目标点B=(0.8,0.4),规划时间t=100 s.
| 刚体 | li /m | ri /m | mi /kg | Ii /(kg·m2) |
| 0 | 0.5 | 0.5 | 400 | 66.67 |
| 1 | 1.0 | 1.0 | 40 | 3.33 |
| 2 | 0.5 | 0.5 | 30 | 2.50 |
首先采用避奇异轨迹规划获得机械臂末端在PDW区域内使系统不发生动力学奇异的初始基座姿态角阈值. 选取边界曲线S0=10,那么联立式(15)、 (16)解得末端交点处系统的基座姿态角及机械臂关节角值(θF0,qF1,q2F)为
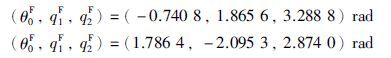
将上述端点值代入式(6)中,联立式(14)得到在直线避奇异规划初始点位置的基座姿态角. 解得基座姿态角避奇异阈值θin0,1=1.6°,θin0,2=107.7°.
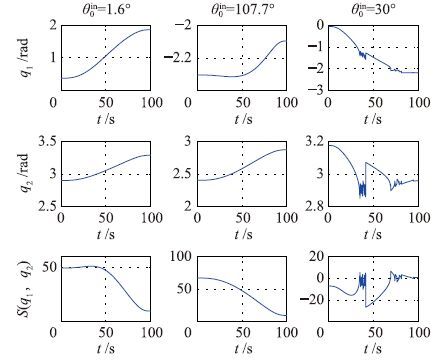
由图 5可以直观地看出,当末端在点C处基座姿态角取θin0=30°(θin0,1≤θin0≤θin0,2),系统在运动过程中出现S(q1,q2)=0的情况,从而出现动力学奇异问题并导致机械臂末端无法按预期轨迹运动. 而当θin0分别取边界阈值时,系统在运动末时满足S=10并保证了整个运动过程不发生动力学奇异.
|
| 图 5 基座初始姿态角取不同值关节角变化曲线 Fig. 5 Joint angle trajectories in different spacecraft attitude |
基于此,当末端在初始点C处基座姿态角θ0in满足θ0in≤θ0,1in or θ0,2in≤θ0in时,机械臂在运动过程中系统不会发生奇异. 根据上述分析,在避奇异阈值范围内选取初始点C处θ0in=0°,那么对应的C点基座姿态角及关节角值为
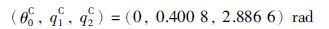
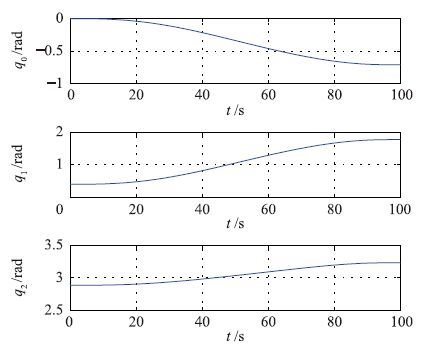
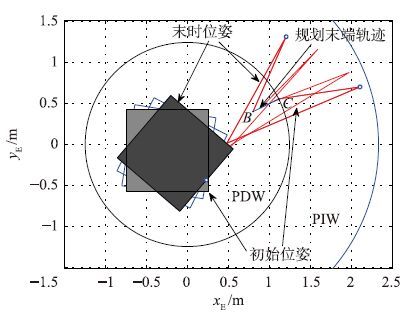
将C点处基座姿态角和机械臂关节角值作为初始值代入式(6)中,联立式(14)可以得到系统基座姿态角及机械臂关节角变化曲线如图 6所示,其平面运动图如图 7所示. 可以看出,规划出的末端运动满足期望轨迹并避免了动力学奇异的发生.
|
| 图 6 系统关节角及基座姿态角变化曲线图 Fig. 6 Spacecraft attitude and joint angle trajectories |
|
| 图 7 空间机械臂避奇异平面运动图 Fig. 7 Motion animation of space manipulator avoiding singularity |
选取跟踪误差权值矩阵Q=diag{120,250},控制力矩权值矩阵R=diag{0.001,0.01},各参数量初始值由轨迹规划部分给出. 为了突出SDRE控制的有效性,仿真比较了在模型相同情况下,PD控制器的控制效果. 所设计PD控制器为
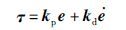
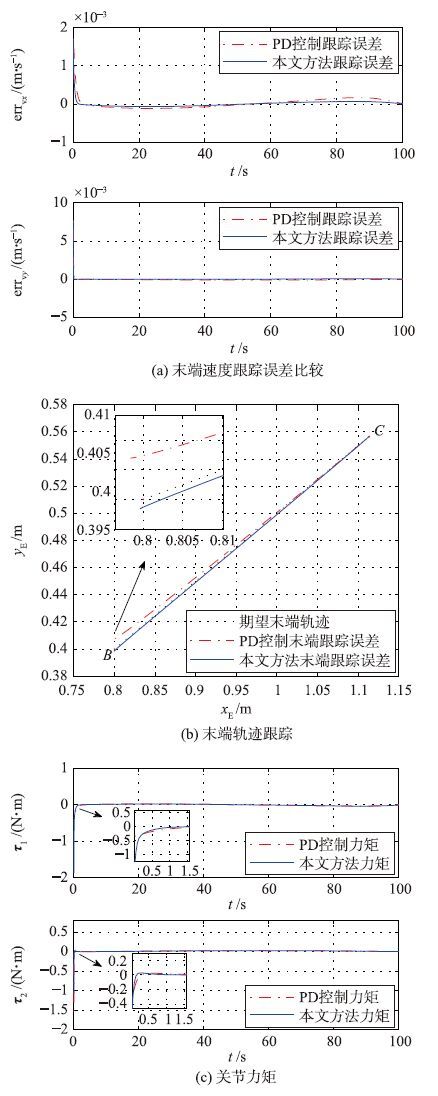
|
| 图 8 本文方法与PD控制比较 Fig. 8 Comparisons between the proposed method and PD controller |
图 8(a)、 图 8(b)分别显示了不同跟踪控制方法的末端速度轨迹跟踪误差情况以及末端轨迹跟踪情况. 可以看出,与PD控制相比,本文所设计的控制器跟踪误差更小,表现出更高的跟踪精度. 图 8(c)显示了对末端速度轨迹
跟踪过程中关节力矩的变化情况. 可以看出,SDRE控制器产生的力矩变化要比PD控制调节时间更快,更能够满足实际工程的需求. 进一步,分别计算满足式(20)的SDRE控制器与PD控制器的速度输出跟踪指标J1,J2. 通过计算得到SDRE控制的指标函数值J1=0.057 2,PD控制的指标函数值J2=0.396 5. 证明了SDRE控制器作为一种优化控制器,具有更好的跟踪控制性能.
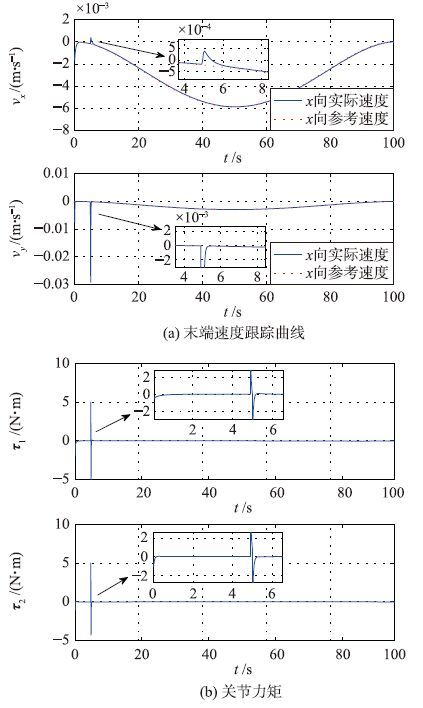
为了更好地满足实际工程的需求,考虑在跟踪的过程中存在脉冲干扰作用于各关节力矩上. 即在t=4.9 s时,加入一个幅值为5 N·m,长度为0.1 s的脉冲. 仿真结果如图 9所示.
|
| 图 9 脉冲干扰下所提方法控制器仿真结果 Fig. 9 Simulation results of the proposed method with impulse interference |
从图 9(a)、 图 9(b)的跟踪速度变化和各关节力矩变化可以看出,本文所设计的SDRE优化控制器具有良好的抗干扰能力,在脉冲干扰的影响下迅速跟踪上期望轨迹,并且各关节力矩变化能够满足实际的工程需求.
5 结论本文在对二连杆自由漂浮空间机器人进行动力学和奇异性分析的基础上,设计了一种避奇异规划—跟踪算法,使机械臂末端能够在PDW区域内完成跟踪控制任务,从而更充分地利用了自由漂浮空间机器人的工作空间. 通过设定安全边界曲线,获取避奇异阈值,为跟踪控制器配置初始参数并规划出一条能够回避动力学奇异的参考轨迹. 在此基础上,采用状态依赖Riccati方程设计跟踪控制器,实现对末端运动的准确跟踪. 仿真结果验证了算法具有较高的跟踪精度,同时具有抗输入干扰的能力. 下一步的工作将关注在参数不确定条件下避奇异规划—跟踪算法的设计.
| [1] | Angel F A, Ou M, Khanh P, et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in Aerospace Sciences, 2014, 68(1): 1-26. |
| [2] | 翟光, 张景瑞, 周志成. 静止轨道卫星在轨延寿技术研究进展[J]. 宇航学报, 2012, 33(7): 122-134. Zhai G, Zhang J R, Zhou Z C. A review of on-orbit life-time extension technologies for GEO satellites[J]. Journal of Astronautics, 2012, 33(7): 122-134. |
| [3] | Xu W F, Zhang J T, Qian H H, et al. Identifying the singularity conditions of Canadarm2 based on elementary jacobian transformation[C]//IEEE International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2013: 795-800. |
| [4] | Nakamura Y, Hanafusa H. Inverse kinematic solutions with singularity robustness for robot manipulator control[J]. Transactions of ASME Journal of Dynamic Systems, Measurement and Control, 1986, 108(2): 163-171. |
| [5] | 徐文福, 梁斌, 刘宇, 等. 一种新的PUMA类型机器人奇异回避算法[J]. 自动化学报, 2008, 34(6): 670-675. Xu W F, Liang B, Liu Y, et al. A novel approach to avoid singularities of PUMA-type manipulators[J]. Acta Automatica Sinica, 2008, 34(6): 670-675. |
| [6] | Nenchev D, Umetani Y, Yoshida K. Analysis of a redundant free-flying spacecraft manipulator system[J]. IEEE Transactions on Robotics and Automation, 1992, 8(1): 1-6. |
| [7] | 张福海, 付宜利, 王树国. 自由漂浮空间机器人回避动力学奇异的轨迹规划[J]. 机器人, 2012, 34(1): 38-43. Zhang F H, Fu Y L, Wang S G. Trajectory planning of free-floating space robot with avoidance of dynamic singularity[J]. Robot, 2012, 34(1): 38-43. |
| [8] | Papadopoulos E, Dubowsky S. Dynamic singularities in the control of free-floating space manipulators[J]. ASME Journal of Dynamic Systems, Measurement and Control, 1993, 115(1): 44-52. |
| [9] | Nanos K, Papadopoulos E. On cartesian motions with singularities avoidance for free-floating space robots[C]//IEEE International Conference Robotics and Automation. Piscataway, NJ, USA: IEEE, 2012: 5398-5403. |
| [10] | Cimen T. Development and validation of mathematical model for control of constrained non-linear oil tanker motion[J]. Mathematical and Computer Modeling of Dynamical Systems: Methods, Tools and Applications in Engineering and Related Sciences, 2009, 15(1): 17-49. |
| [11] | Innocenti M, Baralli F, Salotti F, et al. Manipulator path control using SDRE[C]//Proceedings of the American Control Conference. Piscataway, NJ, USA: IEEE, 2000: 3348-3352. |
| [12] | Korayem M H, Khademi A, Nekoo S R. A comparative study on SMC, OSMC and SDRE for robot control[C]//Proceedings of the 2nd International Conference on Robotics and Mechatronics. Piscataway, NJ, USA: IEEE, 2014: 013-018. |
| [13] | Xin M, Balakrishnan S N, Huang Z W. Robust state dependent Riccati equation based robot manipulator control[C]//IEEE International Conference on Control Applications. Piscataway, NJ, USA: IEEE, 2001: 369-373. |
| [14] | Fenili A, Balthazar J M. The rigid-flexible nonlinear robotic manipulator: Modeling and control[J]. Commun Nonlinear Sci Numer Simulat, 2011, 16(5): 2332-2341. |
| [15] | Tortopidis I, Papadopoulos E. On point-to-point motion planning for underactuated space manipulator systems[J]. Robotics and Autonomous Systems, 2007, 55(1): 122-131. |
| [16] | 刘正雄, 鹿振宇, 黄攀峰. 基于递推差分进化算法的空间机器人参数辨识[J]. 宇航学报, 2014, 35(10): 1127-1134. Liu Z X, Lu Z Y, Huang P F. Parameter identification of space robot based on recursive different evolution algorithm[J]. Journal of Astronautics, 2014, 35(10): 1127-1134. |
| [17] | 石忠, 王永智, 胡庆雷. 基于多项式插值的自由漂浮空间机器人轨迹规划粒子群优化算法[J]. 宇航学报, 2011, 32(7): 1516-1521. Shi Z, Wang Y Z, Hu Q L. A polynomial interpolation based particle swarm optimization algorithm for trajectory planning of free-floating space robot [J]. Journal of Astronautics, 2011, 32(7): 1516-1521. |
| [18] | 丰保民, 马广程, 温奇咏, 等. 任务空间内空间机器人鲁棒智能控制器设计[J]. 宇航学报, 2007, 28(4): 914-919. Feng B M, Ma G C, Wen Q Y, et al. Design of robust intelligent controller for space robot in task space[J]. Journal of Astronautics, 2007, 28(4): 914-919. |
| [19] | 薛晗, 李迅, 彭胜军, 等. 空间机器人随机故障容错规划的蜜蜂算法[J]. 信息与控制, 2009, 38(6): 725-734. Xue H, Li X, Peng S J, et al. Fault tolerance planning of space robot subject to stochastic breakdown using honey bee algorithm[J]. Information and Control, 2009, 38(6): 725-734. |
| [20] | Banks H T, Lewis B M, Tran H T. Nonlinear feedback controllers and compensators: a state-dependent Riccati equation approach[J]. Computational Optimization and Application, 2007, 37(2): 177-218. |



