2. 贵州大学大数据与信息工程学院, 贵州 贵阳 550025
2. College of Big Data & Information Engineering, Guizhou University, Guiyang 550025, China
以生物智能为依托的智能优化在漫长历程中已得到快速发展[1, 2, 3, 4],大量源于生物灵感的新型优化算法不断涌现,以至于探讨收敛速度快的微种群优化算法已成为智能优化的发展趋势. 特别,依据果蝇觅食行为机制产生的基本果蝇优化算法(basic fly optimization algorithm,BFOA)[5],因其结构简单、 可操作性强等优点[7],已受到较多学者的足够重视. 该算法的设计初衷是以果蝇嗅觉感知食物远近和以视觉感知食物所在方向为生物理论基础,以解决连续函数优化问题为目的. 继后,围绕算法的收敛性和单、 多果蝇的位置更新策略,国内外对其展开了一系列研究[7-19],且部分成果在控制设计、 预测、 故障诊断、 支持向量机等方面已得到应用[20-22]. 研究工作集中在探讨改进型、 新型、 混合型果蝇优化算法和算法的应用.
鉴于BFOA要求个体评价量大,个体更新规则对果蝇与食物源位置之间的距离依赖程度高、 个体间信息交互能力弱等缺陷,目前主要集中在探讨BFOA的改进型算法[7-15]; 例如,针对局部搜索、 收敛精度等[7-8, 10, 14],通过引入细菌迁徙操作、 混沌变异、 混合蛙跳更新策略等,提高种群多样性,增强局部搜索能力; 针对种群的初始位置以及固定搜索步长对寻优效率和收敛速度的影响[9, 11, 12, 15],通过融入Logisitic映射、 种群划分以及动态递减步长的更新策略,加快算法的寻优效率和收敛速度; 针对果蝇浓度值始终为非负的问题,文[13]将决策区间转化为对称区间,克服了目标函数的变量值被要求为非负的限制. 近年来,新型果蝇优化算法的研究也已取得一定进展,主要集中在利用果蝇协同觅食行为探讨协同进化果蝇优化算法[16-17]. 主要目的在于通过引入协同进化的更新策略,增强算法跳出局部搜索的能力. 例如,文[16]通过动态划分子群,引入混沌映射,不同子群执行不同进化策略,有效弥补了寻优精度低、 易陷入局部搜索的不足,但因群体规模较大,搜索效率受到影响; 文[17]结合进化过程中产生的最好与最差个体,对进化个体进行更新,一定程度上缓解了早熟现象.
综上,果蝇优化算法的研究仍处于初步阶段,新型果蝇优化算法、 算法收敛速度和理论分析以及算法处理高维优化问题的优势与缺陷等研究均有待陆续展开. 基于此,本文借鉴果蝇的嗅觉对事物的感知行为和视觉神经的方向选择特征,以小种群进化为载体,依据果蝇协同觅食的生物特征设计进化框架,力求探讨具有种群规模小、 参数少、 收敛速度快的小种群果蝇优化算法,简称微果蝇优化算法(micro fly optimization algorithm,μFOA). 比较性的数值实验结果显示,该算法在解的搜索质量方面具有明显优势,对高维函数优化问题的求解具有一定的应用潜力.
2 问题描述与果蝇基本理论考虑如下静态优化问题(P)
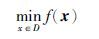
果蝇通过嗅觉和视觉[23]感知附近食物源的大体方位和远近,利用复眼捕捉周围环境信息. 就嗅觉而言,果蝇的嗅觉器官能很好地搜集到漂浮在空气中的气味分子. 研究表明,果蝇的嗅神经元能被用于检测和识别已感知到的化学气味分子,这些气味信息在嗅神经元内转换成神经电信号,并经嗅神经元的轴突传递到触角叶,再经投射神经元将信息送至高级中枢,最终引发行为反应. 另一方面,果蝇的复眼是一种极为重要的光感受器,其由一个个独立的小眼构成,是快速获取信息的中心[24]. 总之,视觉和嗅觉是决定果蝇能否准确定位和快速发现食物源的重要生理器官. 果蝇通过接收的视觉信号并多次评估,决定何时延伸足部开始着陆. 之后,利用背景中的视觉信号定位食物源的大致方位; 利用嗅觉信号判断食物源的远近. 凭借视觉和嗅觉信号,不断调整觅食的行为,逐渐靠近食物源的位置.
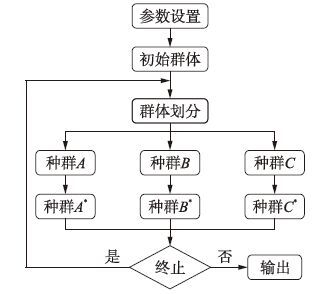
3 算法原理与算法设计μFOA主要由群体划分和子群进化两个模块构成,如图 1所示. 群体划分主要依据群体中个体的适应度,将进化群体划分为优质子群(种群A)、 中等子群(种群B)和劣质子群(种群C). 种群进化中产生的最好个体被视为可能的食物源,各种群依据特定的变异方式和历史信息更新自身位置,并产生新一代群体. 为便于算法描述,将果蝇(个体)与以上问题(P)的候选解对应,食物源视为该问题本身. 结合图 1和以上果蝇生物行为特性,μFOA的具体描述如下:
|
| 图 1 μFOA的流程图 Fig. 1 Flowchart of μFOA |
Step 1 输入参数: 群体规模N,迭代数Gmax,选择率α,β.
Step 2 置t←1,随机产生N个个体构成初始群体P(t),依据个体适应度,将P(t)中最好、 最差个体分别作为当前最好个体xbest和最差个体xworst.
Step 3 依据个体适应度升幂排列P(t)中所有个体,个体排序后,前面的αN个个体构成优质种群A、 后面的βN个个体构成劣质种群C,其余的构成中等种群B.
Step 4 种群A、 B、 C分别执行如下更新步骤:
Step 4.1 种群A中个体x按如下方式更新
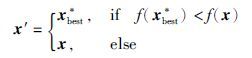
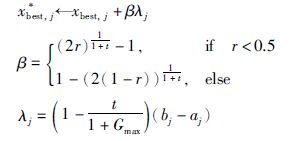
Step 4.2 种群B执行如下变异策略:

Step 4.3 种群C执行如下变异:
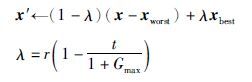
Step 4.4 组合种群A*、 B*和C*为p(t+1).
Step 4.5 经由Step 4.1至Step 4.3中最好和最差个体,对xbest和xworst分别实施更新.
Step 5 若t<Gmax,则t←t+1,转Step 3; 否则,输出xbest.
在以上算法设计中,种群A中个体利用单点多项式变异执行局部搜索,此模拟果蝇着陆后,借助视觉信号捕捉食物源的大致方位,使个体逐渐向食物源(最优解)所在方向转移; B种群利用非均匀变异使个体向最好个体附近转移,产生优质和多样的个体,此模拟果蝇嗅觉对食物源的感知行为,借以增强群体多样性; 受果蝇视觉和嗅觉综合行为特征的启发,种群C利用类似于均匀变异的变异方式,使种群个体在最优个体best与最差个体worst间发生变异,扩大个体的搜索范围,并不断向最优个体的位置靠近. 在设计上,与BFOA相比,回避了利用食物源的味道浓度及果蝇与食物源的距离确定决策变量值的限制. 此算法的结构较为简单,可调参数仅有α,β,各子群体的更新方式不同,群体的进化具有较好的自适应性.
4 计算复杂度分析

以上表明,μFOA的计算复杂度由问题维数和群体规模确定,加之群体规模设置为较小值,因此该算法的运行速度能得到保证.
5 数值实验在Window XP/CPU 2.50 GHz/RAM 3.0 GB/VC++环境下展开数值实验. 选择具有竞争力的2种新的果蝇优化算法FFO(fruit fly optimization)[5-6]和IFFO(improved fruit fly optimization)[18]参与比较分析. 测试问题包括13个单模态优化问题(F1~F13)[18]和7个多模态函数优化问题(F14~F20)[18],见附录. 每种测试问题的维数取30、 50、 100或200. 各算法求解每种测试问题100次,其种群规模均为6,单次运行的总评价数为1 200. FFO和IFFO的参数最佳设置与相应文献的相同. μFOA仅包含两个可调参数,算法调试后,对于各测试问题均设置α=β=0.2. 为充分检测μFOA的行为特性,算法比较分析包括: 研究以上算法求解偏低维(30或50)、 偏高维(100或200)测试问题时的性能差异,依据算法运行时间比较搜索效率差异,以及借助假设检验,分析这些算法在搜索效果方面的显著差异性.
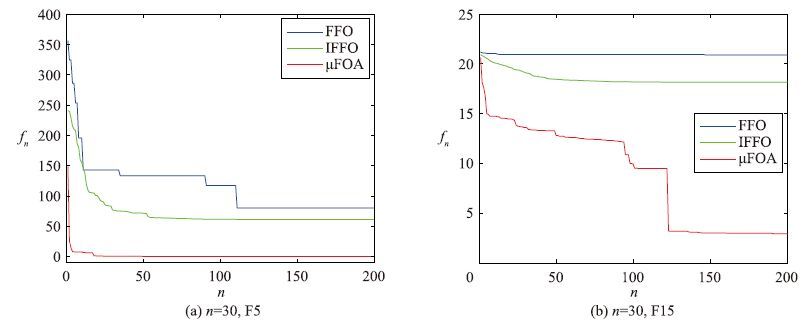
5.1 偏低维实验结果比较分析在维数设定为30、 50前提下,以上算法分别独立求解每个测试问题100次后,获得的统计结果如表 1、2所示. 以F5、 F15为例,各算法获得的目标值的平均搜索曲线如图 2、 3所示. 图中,fn表示100次运行下第n代群体的最小目标值的均值.
| Algor. | F1 | F2 | F3 | F4 | F5 | F6 | F7 | |||||||
| μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | |
| FFO | 2 333 | 111 | 1 127 | 477 | -0.04 | 10-3 | >104 | 103 | 80.2 | 10-14 | >104 | 104 | >105 | 0 |
| IFFO | 9 216 | 335 | >105 | 104 | -0.44 | 10-2 | >104 | 103 | 61.3 | 10-13 | - | - | >104 | 0 |
| μFOA | 1 856 | 0 | 0.79 | 0.08 | -1 | 0 | 0.04 | 0.09 | 10-3 | 10-3 | 28.8 | 0.12 | 0.01 | 0.001 |
| Algor. | F8 | F9 | F10 | F11 | F12 | F13 | F14 | |||||||
| FFO | 78 | 2.0 | 145.6 | 0 | >104 | 103 | >104 | 0 | - | - | 1688 | 0 | 47.9 | 7.9 |
| IFFO | 75.4 | 2.0 | 57.1 | 0 | >104 | 103 | >104 | 0 | - | - | 104 | 0 | 8.64 | 0 |
| μFOA | 40.2 | 0 | 0.05 | 0.2 | 30 | 0 | 0 | 0 | 30 | 0 | 465 | 0 | 10-4 | 10-6 |
| Algor. | F15 | F16 | F17 | F18 | F19 | F20 | ||||||||
| FFO | 20.9 | 0.08 | 886 | 18.3 | >107 | 0 | 364 | 0 | -5.04 | 0.71 | - | - | ||
| IFFO | 18.2 | 0.2 | 271 | 27 | >106 | 105 | 165 | 26.5 | -8.26 | 0.78 | - | - | ||
| μFOA | 2.9 | 1.1 | 0 | 0 | -569 | 225 | 16.4 | 44.3 | -9.12 | 2.4 | 258 | 200 | ||
| 注: μ为独立运行100次后获得的目标值的均值,σ为独立运行100次后获得的目标值的均方差,表中“-”表示获得的平均目标值较大. | ||||||||||||||
| Algor. | F1 | F2 | F3 | F4 | F5 | F6 | F7 | |||||||
| μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | |
| FFO | 8 595 | 254 | 9 045 | >103 | -10-4 | 10-5 | >105 | 103 | 298 | 0 | >105 | 105 | >105 | 104 |
| IFFO | >104 | 0 | >106 | >105 | -0.05 | 0.01 | - | - | 79.8 | 0 | - | - | >105 | 104 |
| μFOA | 5 096 | 0 | 0.99 | 0.01 | -1 | 0 | >104 | 104 | >10-5 | 10-5 | 48.6 | 0.13 | >103 | 103 |
| Algor. | F8 | F9 | F10 | F11 | F12 | F13 | F14 | |||||||
| FFO | 82.5 | 0 | - | - | >104 | 104 | >104 | 3 374 | - | - | 7 437 | 174 | 83.7 | 0 |
| IFFO | 87.9 | 0 | - | - | >104 | 2 898 | >104 | 0 | - | - | >105 | 5 383 | 31.1 | 2 |
| μFOA | 37.6 | 0 | 10-3 | 10-4 | 50 | 0 | 0 | 0 | - | - | 1275 | 0 | >10-4 | 10-3 |
| Algor. | F15 | F16 | F17 | F18 | F19 | F20 | ||||||||
| FFO | 20.9 | 0.07 | 1 372 | 11.6 | - | - | 734 | 15 | -5.47 | 0.56 | - | - | ||
| IFFO | 19.4 | 0.08 | 800 | 75.1 | - | - | 363 | 5.1 | -11.9 | 1.4 | - | - | ||
| μFOA | 4.78 | 2.59 | 0 | 0 | -2 338 | 195 | 10-5 | 10-5 | -24.2 | 17.4 | 2 539 | 104 | ||
|
| 图 2 30维的F5、 F15的平均搜索曲线比较 Fig. 2 Comparison of average search curves for F5 and F15 with 30 dimensions |
|
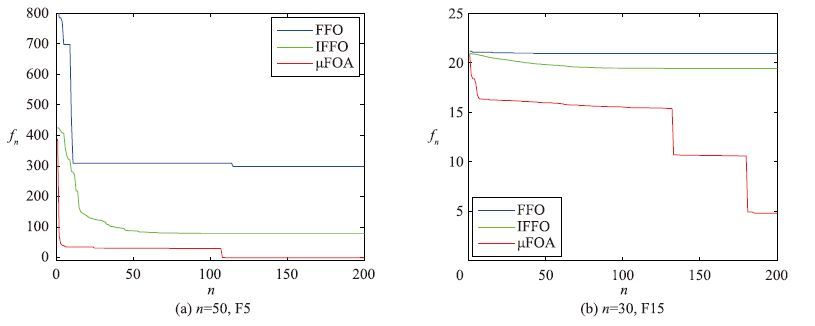
| 图 3 50维的F5、 F15的平均搜索曲线比较 Fig. 3 Comparison of average search curves for F5 and F15 with 50 dimensions |
由表 1中平均值可知,当处理以上30维优化问题时,μFOA除了求解F19的优势不十分突出外,求解其它测试问题均有明显的优势,此说明该算法的局部和全局搜索能力强. FFO求解F8、 F15获得的效果与IFFO的差异较小,且求解F2、 F13获得的效果比IFFO的效果要好,但求解其它问题获得的均值都较大,说明此算法易陷入局部搜索. 导致此现象的主要原因在于该算法的个体更新方式单一,制约了算法的搜索效果,因此该算法的进化能力和群体多样性均有待改善; IFFO求解以上20个30维测试问题,获得的效果均差于μFOA的效果,求解9个测试问题(例如F3、 F5、 F9)获得的效果比FFO获得的效果要好(见图 2). 另外,从表 1中均方差获知,FFO和IFFO的搜索效果极不稳定,且较容易陷入局部搜索,特别是求解多模态函数优化问题(F14~F20),获得的效果极不理想. 然而,μFOA除了求解F17、 F18获得的均方差偏大外,求解其它问题获得的效果均相对较为稳定. 图 2反映了FFO和IFFO易陷入局部搜索.
通过对比表 1、 表 2说明随着维数的增加,FFO和IFFO的寻优能力逐渐退化,主要原因在于它们的算法结构导致它们易陷入局部搜索和全局开采能力弱(见图 3). 可是,μFOA借助自适应更新方式,几乎都能获得理想的目标值,极大减少了陷入局部搜索的可能性,其获得的解的质量受到维数的影响较小; 图 2、 3表明该算法仅出现寻优速度变慢的现象(除F4及F12外). 对于以上全局最优解的位置在坐标原点的优化问题,FFO和IFFO均较难获得近似解,说明此两种算法在搜索后期的局部勘测能力弱,获得的最好解与理论最优解相距较远. 另外,对于全局最优解的位置不在坐标原点且目标值为0的优化问题(如F6、 F20),FFO和IFFO在算法运行初期就已陷入局部搜索,因此这两种算法的进化方式有待改善. 另外,以上均方差表明,FFO和IFFO易于陷入局部搜索且搜索效果不稳定; 除F4、 F12和F20外,μFOA均能稳定地获得较为理想的结果,此进一步说明该算法求解50维以下的单、 多模态函数优化问题能获得满意效果.
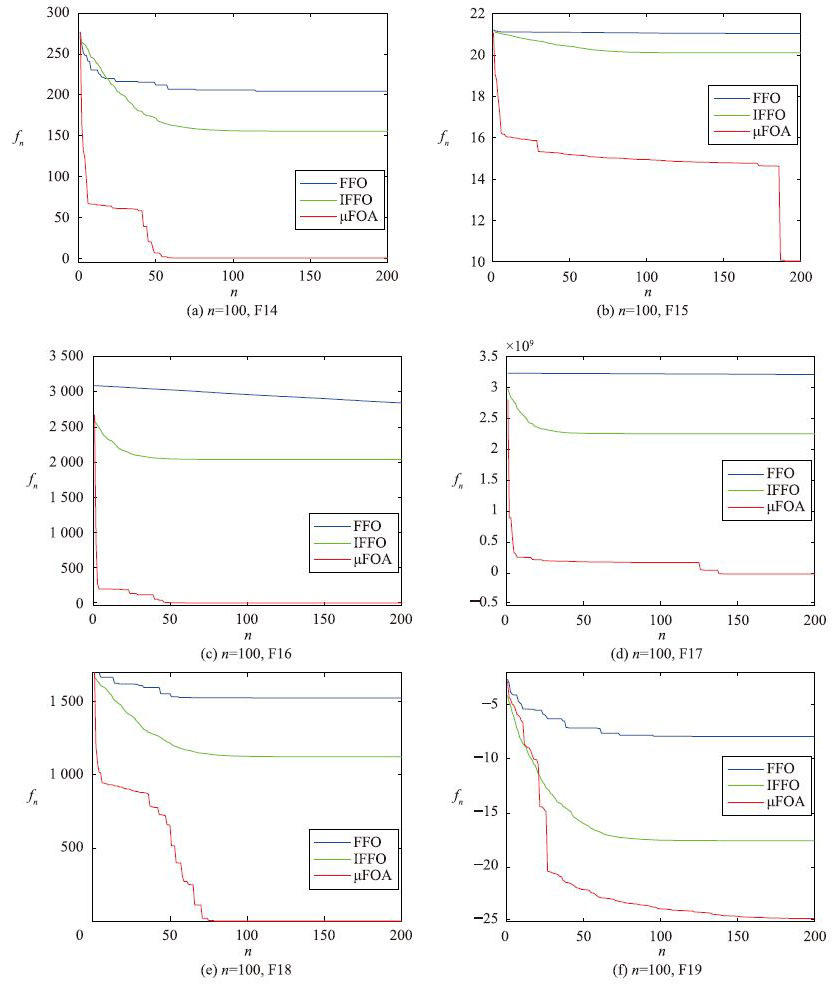
5.2 偏高维实验结果比较分析取定维数为100、 200,以上3种算法各自求解F1~F20之后,获得的统计结果如表 3、 4所示. 以F14~F19为例,各算法的平均搜索曲线如图 4、 5所示.
| Algor. | F1 | F2 | F3 | F4 | F5 | F6 | F7 | |||||||
| μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | |
| FFO | 52 461 | 209 | >105 | 105 | -10-8 | 10-8 | >105 | 104 | 2 286 | 23 | >107 | 106 | >105 | 104 |
| IFFO | >105 | 8 133 | >107 | 106 | -10-5 | 10-5 | >108 | 108 | 939 | 208 | >108 | 107 | >105 | 105 |
| μFOA | 20 196 | 0 | 111 | 160 | -1 | 0 | >104 | 105 | 0.02 | 0.01 | 98.2 | 0.2 | >105 | 104 |
| Algor. | F8 | F9 | F10 | F11 | F12 | F13 | F14 | |||||||
| FFO | 87.7 | 2 | 504 | 0 | >105 | 3 537 | >105 | 104 | - | - | >105 | 104 | 205 | 22.5 |
| IFFO | 96.9 | 0 | 419 | 1.36 | >105 | 5 064 | >105 | 104 | - | - | >106 | 104 | 155 | 7 |
| μFOA | 53.2 | 4.6 | 0.05 | 0.09 | 100 | 0 | 0 | 0 | - | - | 5 050 | 0 | 10-4 | 10-3 |
| Algor. | F15 | F16 | F17 | F18 | F19 | F20 | ||||||||
| FFO | 21 | 0.03 | 2 842 | 54.1 | >109 | 108 | 1 525 | 19.5 | -7.92 | 1.2 | - | - | ||
| IFFO | 20.1 | 0.06 | 2 039 | 27.5 | >109 | 108 | 1 124 | 52.8 | -17.6 | 1.9 | - | - | ||
| μFOA | 10 | 6.3 | 10-3 | 10-3 | -5 272 | 356 | 0.04 | 0.06 | -24.7 | 26.8 | 2 898 | 2 213 | ||
| Algor. | F1 | F2 | F3 | F4 | F5 | F6 | F7 | |||||||
| μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | |
| FFO | >105 | 103 | >107 | 106 | 0 | 0 | >105 | 104 | >104 | 104 | >108 | 107 | >106 | 106 |
| IFFO | >105 | 104 | >108 | 106 | 0 | 0 | >108 | 108 | >104 | 673 | >109 | 108 | >106 | 106 |
| μFOA | 80 396 | 0 | 0.99 | 0.27 | -1 | 0 | >104 | 104 | 0.009 | 0.01 | 198 | 3.84 | >105 | 105 |
| Algor. | F8 | F9 | F10 | F11 | F12 | F13 | F14 | |||||||
| FFO | 91.7 | 0.79 | - | - | >105 | 104 | >105 | 104 | - | - | >106 | 105 | 465 | 18.1 |
| IFFO | 99 | 0.23 | 928 | 47.3 | >105 | 104 | >105 | 104 | - | - | >106 | 105 | 428 | 6.6 |
| μFOA | 54 | 10.1 | 10-5 | 10-5 | 200 | 0 | 0 | 0 | 200 | 0 | 20 100 | 0 | >10-8 | 10-8 |
| Algor. | F15 | F16 | F17 | F18 | F19 | F20 | ||||||||
| FFO | 21.1 | 0.07 | 5 472 | 310 | - | - | 3 250 | 46.8 | -10.8 | 1.1 | - | - | ||
| IFFO | 20.6 | 0.06 | 4 828 | 267 | - | - | 2 817 | 55.6 | -23.3 | 3.06 | - | - | ||
| μFOA | 5.1 | 4.7 | 10-8 | 10-7 | -7 552 | 104 | 0.12 | 0.35 | -55.1 | 65.2 | 11 654 | 8 775 | ||
|
| 图 4 100维的F14~F19的平均搜索曲线比较 Fig. 4 Comparison of average search curves for problems F14 to F19 with 100 dimensions |
|
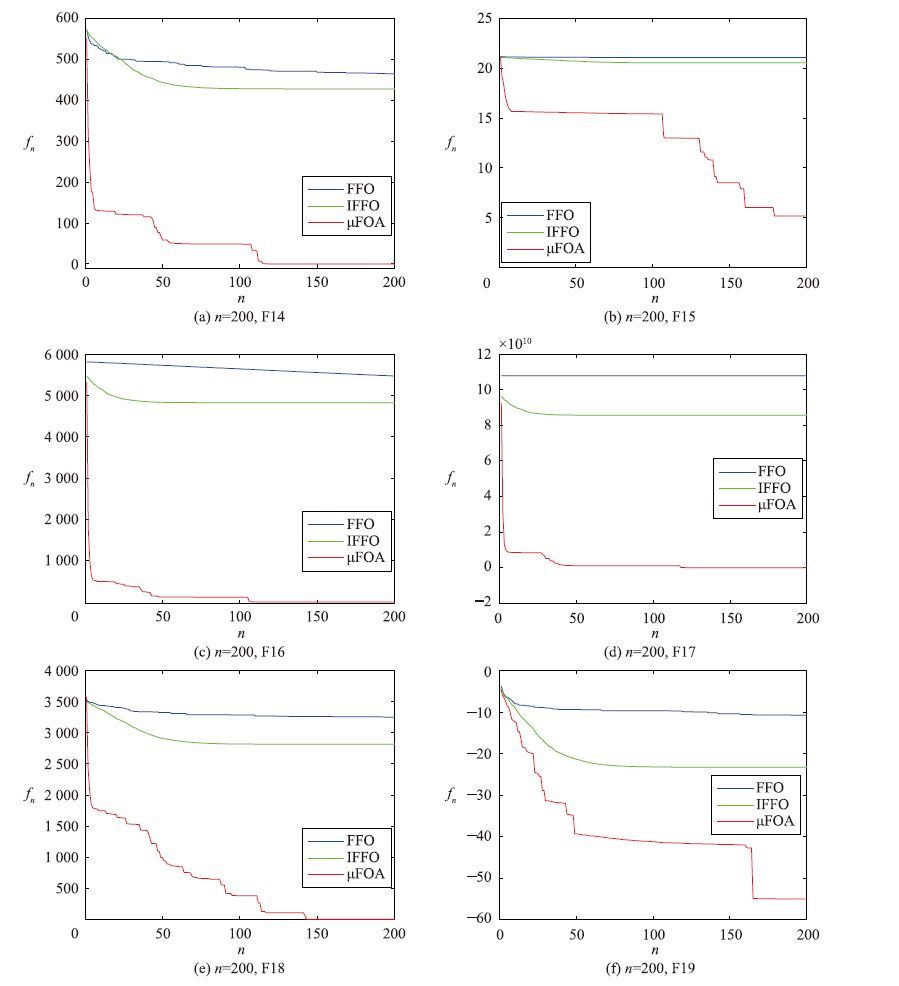
| 图 5 200维的F14~F19的平均搜索曲线比较 Fig. 5 Comparison of average search curves for problems F14 to F19 with 200 dimensions |
经由表 3获知,FFO和IFFO求解绝大部分测试问题,获得的均值与理论上的最小值相差较大,仅有求解F8、 F15、 F19能获得相对较小的平均目标值. 它们求解测试问题获得的效果几乎都差于μFOA获得的效果,此说明FFO和IFFO求解100维的单、 多峰值优化问题的能力较弱,而μFOA的寻优能力受到维数影响尚小(除F4和F12外). 另外,表 3中的均方差和图 4表明,μFOA的寻优效果整体上较稳定,获得的解质量较高,收敛速度快,而另外两种算法的寻优效果较差,主要源于FFO更新方式单一,进化群体中的个体以相同方式向当前最优个体位置靠近; IFFO的进化群体中的个体都在最优个体附近执行单点变异,降低了种群的多样性,致使算法易陷入局部搜索.
表 4说明,随着维数增大,FFO和IFFO几乎不能有效求解以上测试问题,仅有求解F8、 F15、 F19时,获得的平均目标值偏小,此进一步反映了它们的整体搜索能力弱和多样性差; 当然,μFOA不能有效求解的问题个数也在增加(F14~F19). 由此看出,求解高维多峰值优化的全局最优解具有极大的挑战性. 经由图 5,μFOA获得的解质量较高、 收敛速度快,而FFO和IFFO极易陷入局部搜索,寻优能力有待增强,此与以上实验获得的结论一致.
综上,当处理偏高或高维单、 多峰值优化问题时,无论是解质量还是搜索效果的稳定性方面,μFOA均表现出明显的优越性,且在维数低于100情形下,其寻优能力几乎不因维数的增大而受到影响; 可是,由于IFFO和FFO的全局搜索能力和群体多样性有待增强,其寻优质量受到维数的影响较大. 总体上,针对以上20个测试问题,在维数为30、 50、 100、 200情形下,μFOA的寻优能力最强,IFFO总体上比FFO获得的效果要好一些.
5.3 效率比较分析为便于比较分析算法的执行效率,在给定维数下,将以上每种算法独立求解F1~F20中每个测试问题100次所需平均运行时间陈列于表 5.
| Algor. | 30维 | 50维 | 100维 | 200维 | ||||||||
| F1~F19 | F20 | AV | F1~F19 | F20 | AV | F1~F19 | F20 | AV | F1~F19 | F20 | AV | |
| FFO | 0.005 | 0.45 | 0.026 | 0.009 | 1.26 | 0.07 | 0.020 | 5.05 | 0.26 | 0.05 | 20.15 | 1.01 |
| IFFO | 0.005 | 0.46 | 0.027 | 0.009 | 1.25 | 0.07 | 0.021 | 4.93 | 0.26 | 0.05 | 19.84 | 0.99 |
| μFOA | 0.008 | 0.55 | 0.034 | 0.013 | 1.49 | 0.08 | 0.029 | 6.10 | 0.32 | 0.07 | 23.96 | 1.21 |
| 注: 表中第2、 5、 8、 11列中的值是各算法求解F1~F19中每个问题所需的平均运行时间; 表中第3、 6、 9、 12列中的值是各算法独立运行所需的平均运行时间; AV: F1~F20的平均运行时间的平均值. | ||||||||||||
由表 5知,各算法所消耗的平均运行时间随维数加大而增加. FFO和IFFO的执行效率基本相同. μFOA在模块设计上,需依个体适应度进行个体排序,因此,在一定程度上增加了计算量. μFOA比FFO和IFFO的平均运行时间稍长,但基本持平,且此3种算法的运行效率处于同一个数量级.
5.4 显著性差异分析给定维数下,将以上每种算法求解F1~F20中每个测试问题获得的平均目标值作为样本,借助这些样本和多比较方法(Friedman与Friedman秩检验[25]),分析算法获得的解质量是否存在显著性差异. 取显著性水平α=5%,通过查表获知,Χ21-α/2=5.99. 检验结果如表 6所示.
| Dimension | 30 | 50 | 100 | 200 | ||||
| Algorithm | F | FA | F | FA | F | FA | F | FA |
| FFO | 2.7 | 37.25 | 2.45 | 35.4 | 2.45 | 35.2 | 2.5 | 37.1 |
| IFFO | 2.25 | 37.45 | 2.4 | 36.45 | 2.4 | 36.1 | 2.45 | 36.3 |
| μFOA | 1 | 16.6 | 1.1 | 19.35 | 1.1 | 20.05 | 1 | 17.9 |
| Statistic | 27.05 | 23.451 8 | 19.45 | 18.158 1 | 19.45 | 19.953 7 | 25.05 | 21.622 8 |
| 注: F为Friedman检验值; FA为Friedman秩检验值. | ||||||||
经由表 6获知,在给定维数下,μFOA获得的F值和FA值均分别小于另外两种算法获得的对应的值,再加上表中统计值(Statistic)均大于5.99,表明μFOA的解质量与其它两种算法的解质量具有显著性差异. 另外,FFO和IFFO的F值、 FA值均没有明显区别,因此,它们的解质量没有明显差异. 总体上,μFOA较参与比较的FFO和IFFO在所获解的质量方面存在显著性差异; 再结合以上实验结果获知,μFOA在求解质量方面具有明显优势.
6 结论基于果蝇的嗅觉和视觉觅食的行为特征,获得种群规模小、 可调参数少的微果蝇优化算法. 该算法利用优质子群进行局部搜索,增强局部搜索能力. 同时,此子群引导中等子群实施更新; 劣质子群中的个体在当前最好和最差个体之间进行大范围转移,增强群体的多样性. 理论分析表明,该算法的计算复杂度由群体规模和问题的维数确定. 比较性的数值实验表明,此算法在求解质量、 搜索效果的稳定性方面均具明显优势,是一种具有竞争力的小种群果蝇优化算法.
附录 最小化测试问题
| 类型 | 函数 | 决策区域 | 最优解x* | 最小值 |
| f1 | 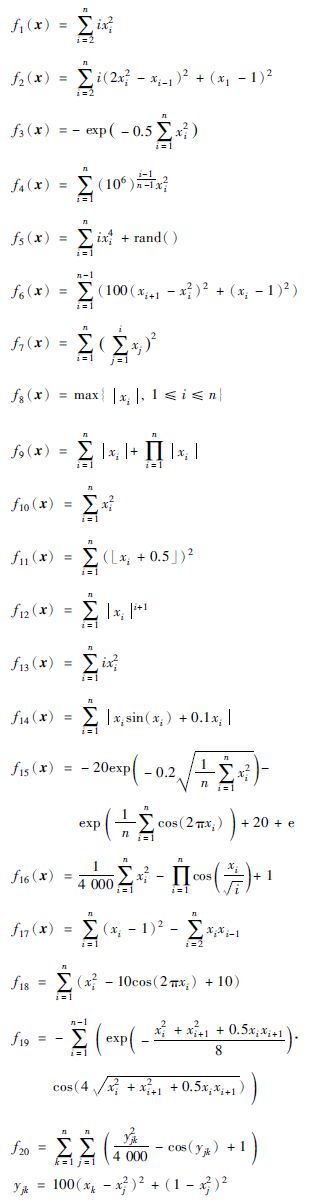 | xi∈[-10, -2] | (-2, -2, …, -2) | 2(n+2)(n-1) |
| f2 | xi∈ [-10, 10] | 0 | 0 | |
| f3 | xi∈ [-1, 1] | 0 | -1 | |
| f4 | xi∈ [-100, 100] | 0 | 0 | |
| f5 | xi∈ [-1.28, 1.28] | 0 | 0 | |
| f6 | xi∈ [-30, 30] | (1, 1, …, 1) | 0 | |
| f7 | xi∈ [-100, 100] | 0 | 0 | |
| f8 | xi∈ [-100, 100] | 0 | 0 | |
| f9 | xi∈ [-10, 10] | 0 | 0 | |
| f10 | xi∈ [-100, -1] | (-1, -1, …, -1) | n | |
| f11 | xi∈ [-100, 100] | 0 | 0 | |
| f12 | xi∈ [1, 10] | (1, 1, …, 1) | n | |
| f13 | xi∈ [1, 30] | (1, 1, …, 1) | n(n+1)/2 | |
| f14 | xi∈ [-10, 10] | 0 | 0 | |
| f15 | xi∈ [-32, 32] | 0 | 0 | |
| f16 | xi∈ [-600, 600] | 0 | 0 | |
| f17 | xi∈ [-n, n2] | x*i=i(n+1-i) | 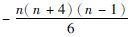 | |
| f18 | xi∈ [-5.12, 5.12] | 0 | 0 | |
| f19 | xi∈ [-5, 5] | 0 | 1-n | |
| f20 | xi∈ [-100, 100] | (1, 1, …, 1) | 0 |
| [1] | 燕乐纬, 陈洋洋, 周云. 一种改进的微种群遗传算法[J]. 中山大学学报: 自然科学版, 2012, 51(1): 50-54. Yan L W, Chen Y Y, Zhou Y. An improved micro-genetic algorithm[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2012, 51(1): 50-54. |
| [2] | 杨燕, 靳蕃, Kamel M. 微粒群优化算法研究现状及其进展[J]. 计算机工程, 2004, 30(21): 3-4. Yang Y, Jin F, Kamel M. Research and development of particle swarm optimization[J]. Computer Engineering, 2004, 30(21): 3-4. |
| [3] | 刘晓峰. 微粒群算法的收敛性及其在工程项目优化中的应用研究[D]. 天津: 天津大学, 2004. Liu X F. Research on convergence analysis of PSO and its application to project optimization[D]. Tianjin: Tianjin University, 2004. |
| [4] | 陈黎卿, 张栋, 陈无畏, 等. 基于微粒子群优化算法的差速器壳体轻量化设计[J]. 农业工程学报, 2013, 29(9): 24-31. Chen L Q, Zhang D, Chen W W, et al. Lightweight design of differential case based on particle swarm optimization algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(9): 24-31. |
| [5] | 潘文超. 果蝇最佳化演算法—最新演化式计算技术[M]. 台北: 沧海书局, 2011: 1-12. Pan W C. A new evolutionary computation approach: Fruit fly optimization algorithm[M]. Taibei: Bookstore of Canghai, 2011: 1-12. |
| [6] | Pan W T. A new fruit fly optimization algorithm: Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74. |
| [7] | 刘成忠, 韩俊英. 基于细菌迁徙的自适应果蝇优化算法[J]. 计算机工程与科学, 2014, 36(4): 690-696. Liu C Z, Han J Y. Adaptive fruit fly optimization algorithm based on bacterial migration[J]. Computer Engineering & Science, 2014, 36(4): 690-696. |
| [8] | 贺智明, 宋建国, 梅宏标. 结合元胞自动机的果蝇优化算法[J]. 计算机应用, 2014, 34(8): 2295-2298. He Z M, Song J G, Mei H B. Fruit fly optimization algorithm based on cellular automata[J]. Journal of Computer Application, 2014, 34(8): 2295-2298. |
| [9] | 宁剑平, 王冰, 李洪儒, 等. 递减步长果蝇优化算法及应用[J]. 深圳大学学报: 理工版, 2014, 31(4): 367-373. Ning J P, Wang B, Li H R, et al. Research on and application of diminishing step fruit fly optimization algorithm[J]. Journal of Shenzhen University: Science and Engineering, 2014, 31(4): 367-373. |
| [10] | 刘成忠, 黄高宝, 张仁陟, 等. 局部深度搜索的混合果蝇优化算法[J]. 计算机应用, 2014, 34(4): 1060-1064. Liu C Z, Huang G B, Zhang R Z, et al. Shuffled fruit fly optimization algorithm with local deep search[J]. Journal of Computer Applications, 2014, 34(4): 1060-1064. |
| [11] | 程慧, 刘成忠. 基于混沌映射的混合果蝇优化算法[J]. 计算机工程, 2013, 39(5): 218-221. Cheng H, Liu C Z. Mixed Fruit fly optimization algorithm based on chaotic mapping[J]. Computer Engineering, 2013, 39(5): 218-221. |
| [12] | 杜军俊. 果蝇优化算法的加权策略研究[J]. 微型机与应用, 2014, 33(16): 67-70. Du J J. Study on the strategy of weighting in fruit fly optimization algorithm[J]. Technique and Method, 2014, 33(16): 67-70. |
| [13] | Dai H, Zhao G, Lu J, et al. Comment and improvement on “A new fruit fly optimization algorithm: Taking the financial distress model as an example”[J]. Knowledge-Based Systems, 2014, 59: 159-160. |
| [14] | Lei X, Du M, Xu J, et al. Chaotic fruit fly optimization algorithm[M]//Advances in Swarm Intelligence. Berlin, Germany: Springer International Publishing, 2014: 74-85. |
| [15] | Yuan X, Dai X, Zhao J, et al. On a novel multiswarm fruit fly optimization algorithm and its application[J]. Applied Mathematics and Computation, 2014, 233: 260-271. |
| [16] | 韩俊英, 刘成忠, 王联国. 动态双子群协同进化果蝇优化算法[J]. 模式识别与人工智能, 2013, 26(11): 1057-1067. Han J Y, Liu C Z, Wang L G. Dynamic double subgroup cooperative fruit fly optimization algorithm[J]. Pattern Recognition & Artificial Intelligence, 2013, 26(11): 1057-1067. |
| [17] | 韩俊英, 刘成忠. 反向认知的高效果蝇优化算法[J]. 计算机工程, 2013, 39(11): 223-225. Han J Y, Liu C Z. Efficient fruit fly optimization algorithm with reverse cognition[J]. Computer Engineering, 2013, 39(11): 223-225. |
| [18] | Pan Q K, Sang H Y, Duan J H, et al. An improved fruit fly optimization algorithm for continuous function optimization problems[J]. Knowledge-Based Systems, 2014, 62: 69-83. |
| [19] | Wang L, Zheng X, Wang S. A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem[J]. Knowledge-Based Systems, 2013, 48: 17-23. |
| [20] | 张维涛. 果蝇优化SVM模型对有机化合物熔点的预测[J]. 广州化工, 2015, 43(5): 128-130. Zhang W T. The prediction of organic compound melting point by SVM optimized by drosophila algorithm[J]. Guangzhou Chemical Industry, 2015, 43(5): 128-130. |
| [21] | 刘宇凯, 胡志坚, 索江镭, 等. 基于果蝇优化算法的广域阻尼控制器设计[J]. 电力系统保护与控制, 2014, 42(24): 25-29. Liu Y K, Hu Z J, Suo J L, et al. Design method of wide-area damping controller based on FOA algorithm[J]. Power System Protection and Control, 2014, 42(24): 25-29. |
| [22] | 洪文鹏, 廖明俊. 基于果蝇优化支持向量机的风机故障诊断研究[J]. 风机技术, 2014, 6: 50-54. Hong W P, Liao M J. Fault diagnosis of fan based on support vector machine of drosophila optimization[J]. Compressor Blower & Fan Technology, 2014, 6: 50-54. |
| [23] | 吴仲南, 邹志华, 杜永均. 果蝇嗅觉分子机理研究进展[J]. 昆虫学报, 2009, 52(7): 799-807. Wu Z N, Zou Z H, Du Y J. Proress in molecular mechanism of olfaction in drosophila melanogaster[J]. Acta Entomologica Sinica, 2009, 52(7): 799-807. |
| [24] | 冷雪, 那杰. 昆虫复眼的结构和功能[J]. 沈阳师范大学学报: 自然科学版, 2009, 27(2): 241-244. Leng X, Na J. Structure and function of insect compound eyes[J]. Journal of Shenyang Normal University: Natural Science, 2009, 27(2): 241-244. |
| [25] | Derrac J, García S, Molina D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm & Evolutionary Computation, 2011(1): 3-18. |
| [26] | Altman E I. Financial Ratios, Discriminant analysis and the prediction of corporate bankruptcy[J]. Journal of Finance, 1968, 23(4): 589-609. |



