2. 南昌航空大学信息工程学院, 江西 南昌 330063;
3. 福建对外经济贸易职业技术学院信息技术系, 福建 福州 350016;
4. 闽江学院电子系, 福建 福州 350108
2. School of Information Engineering, Nanchang Hangkong University, Nanchang 330063, China;
3. Department of Information, Technology Fujian International Business & Economic College, Fuzhou 350106, China;
4. Department of Electronics, College of Minjiang, Fuzhou 350108, China
音圈电机(voice coil motor,VCM)是一种常用的直流直线电机,是依靠直流电驱动的高精度直线执行器,具有结构简单、 响应快速、 精度高等特点,广泛应用于自动对焦镜头、 硬盘磁头等小型线性定位控制系统. 近年来,随着技术的进步,大功率的音圈电机也大量应用于各类工业领域和精密伺服装备上. 随着工作环境复杂性及要求的提高,为提高音圈电机伺服系统的运动精度、 稳定性、 响应速度及鲁棒性等需求,科研人员对其控制方法开展了许多研究[1-4].
PID控制是一种目前应用最为广泛的控制方法,大量的音圈电机伺服系统仍然使用该方法. PID控制中的3个控制参数的不同组合直接影响到控制器的控制效果,在实际应用中,PID参数整定一般是依靠工程师们的经验,因此控制效果受人为因素影响较大. 为解决该问题,文[5]提出一种改进型的遗传算法,对一台并联机床动力学控制实验台的电机伺服系统控制参数进行了优化整定. 但是,实际系统中动力学及负载参数会随着工况发生变化,因此PID方法无法保证稳定的控制性能. Yao等提出了一系列自适应鲁棒控制方法,这类方法能保证存在未知参数及不确定非线性的系统全局稳定性,且保证输出误差在无外扰的情况下渐近趋于0[6-7]. 文[8]针对常规自适应鲁棒控制器参数估计值不能逼近真值的问题,提出了基于复合自适应律的改进方法,该方法同时利用了系统输出误差信息与参数估计误差信息对未知参数进行在线估计,提高了自适应鲁棒控制器的性能. 尽管这些自适应控制方法有助于提高系统的鲁棒性,但收敛性能方面仍存在改进空间. 文[9]将预测控制应用于直线电机的速度和位置的自适应控制中,用紧格式线性化的动态线性时变模型来替代一般非线性系统模型,通过参数估计算法在线估计及预报算法对将来的伪偏导数进行预测,再通过滚动优化实现控制律. 该方法鲁棒性强,但是所需计算量较大. 文[10]将扩张状态观测器(ESO)与非线性PID控制相结合,并通过ESO对扰动进行实时估计,并对扰动进行前馈补偿从而改善控制品质,但文中并未给出严谨的闭环系统稳定性理论分析. 文[11]将基于模糊小脑模型关节控制器(cerebellar model articulation controller,CMAC)和模糊补偿器的混合控制,并引入PID自适应学习算法加速参数学习,该方法得到实验验证,但不易实现. 文[12]采用自适应结合终端滑模控制,利用自适应律获得系统的不确定参数,使得系统取得了较好的跟踪性能. 但该方法必须已知系统质量及力常数,且未考虑变化的外部负载扰动,同时滑模控制也带来“抖颤”问题.
非光滑控制是介于光滑控制与非连续控制之间的一种非线性控制方法. 研究指出,相比于光滑控制,非光滑控制能够有效改善系统收敛速度,并且具有更好的鲁棒性能和抗扰动能力[13-16]. 但非光滑控制对参数型不确定性不具有完全补偿能力,因此该方法与自适应控制存在互补空间.
本文以音圈电机伺服系统为研究对象,针对不确定性问题(包括动力学参数及外部负载扰动)和跟踪控制问题展开研究. 受非光滑控制及自适应控制的启发,设计了一种自适应非光滑控制方法,使得轨迹跟踪控制系统具有自适应及快速收敛能力,并且方法简单、 易于实现.
2 预备知识 2.1 音圈电机伺服系统模型控制对象音圈电机伺服系统动力学可以描述为[12]
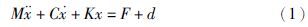
将速度、 加速度记为: v、 a,则动力学方程可以改写为
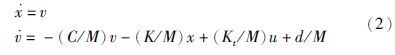
此外,由式(1)可以得到:
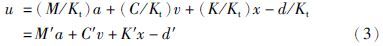

考虑模型参数未知情况下,记名义模型参数为 pn=[Mn Cn Kn dn]T,偏差部分(未知部分)pu=[Mu Cu Ku du]T,则实际参数可以表示为p=pn+pu. 则式(4)可以改写为

对于一致连续函数x(t),如果存在标量函数V和M(t)满足如下条件[18]:
1) V有下界;
2) M(x(t))为连续正定且径向无界;
3) -$\dot{V}$≥M(x),那么,当t→∞时,x(t)→0.
3 自适应非光滑控制假设系统可以测得加速度、 速度及位置,记给定参考位置、 速度、 加速度分别为xd、 vd、 ad,定义: sig(ξ)α=ξαsgn(ξ),0<α<1. 本文设计控制器为
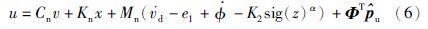
自适应律为
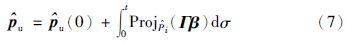
Proj${\hat{P}}$i为向量的投影算子,定义为
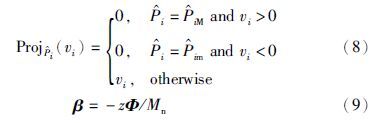
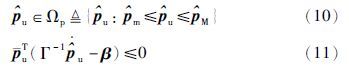
定理 考虑由2.1节中所描述系统,及控制器(6)构成的闭环系统,当t→∞,e1→0、 e2→0,即x→xd、 v→vd.
证明: 由式(5)展开得:
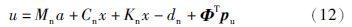
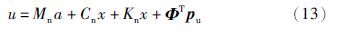
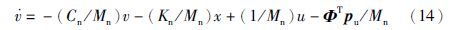
由定义可得:
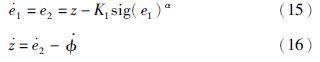
结合控制器式(6)及式(12)等得:
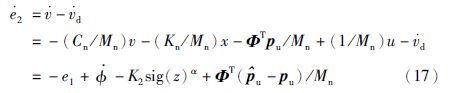
进一步可得:
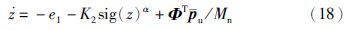
构造李亚普诺夫函数
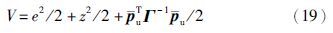
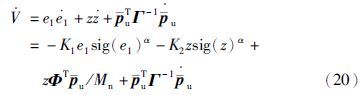
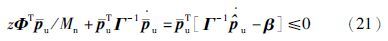
记M(e1,z)=K1e1sig(e1)α+K2zsig(z)α,则:
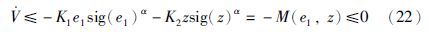
由式(19)、 (21)易知: V有下界且supV1≤V1(0),即上界存在,进一步可以得到: e1,z,${\bar{p}}$有界. 再结合式(15)、 式(18)知:${\dot{e}}$1,${\dot{z}}$有界,因此e1,z为一致连续. 那么M(e1,z)为连续正定且径向无界,根据2.2节中引理可得: 当t→∞时,x→0,z→0,即x→xd、 v→vd.
由于${\dot{\phi }}$(e1)在e1i=0,1i≠0时会出现奇异值,实际应用中定义:
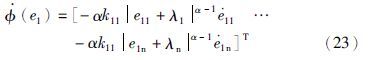
注1 本文所设计方法将非光滑控制与自适应控制相结合,但两种方法的闭环系统分析方面: 自适应控制下闭环系统是时变系统,其收敛性证明一般利用Barbalate引理,而非光滑控制下闭环系统是时不变系统,其收敛性证明一般采用类李亚普诺夫方法(见文[13-16]). 二者的复合控制律设计的主要难点在于闭环系统分析: 自适应控制律下闭环系统是时变系统,类李亚普诺夫方法必然不适用于收敛性证明,而使用Barbalate引理,则需要证明标量函数的微分一致连续,然而幂次项的存在使得其证明极其困难. 为解决这个问题,以新形式Barbalate引理为依据,针对性构造一种自适应非光滑控制方法,使得闭环系统收敛性证明过程回避了上述难点,这也是本文的主要创新之处.
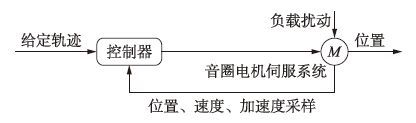
4 仿真实验结果及分析为了验证所设计方法的有效性,本文采用文[12]所给出的仿真对象建立仿真系统(系统参数如表 1所示,仿真系统框图如图 1所示). 实验设计如下: 给定跟踪信号为xd=2×10-4sin(8πt)m(即行程为2 mm,仿真时长1 s). 实验1分别完成: 1) 参数匹配情况(即pu=0). 控制器使用的名义参数与实际系统参数一致. 2) 参数失配情况(pu≠0). 控制器使用的名义参数: Mn=0.4 M、 Cn=0.5 C、 KFnKuin=0.5KFKui、 Kn=0.5 K,外部扰动为d=5cos(16πt)N(即8 Hz,并且在0.5 s时加载到电机),控制器采样频率为10 kHz. ANSC方法参数选择: K1=150、 K2=190、 Γ=diag{40,40,40,400}、 α=0.75、 ${\hat{p}}$m=-pn、 ${\hat{p}}$M=2pn. 此外,对文[12]中的自适应抗饱和滑模控制(adaptive anti-windup sliding mode control,AAWSMC)方法完成实验1仿真(参数见文[12]),并对比实验结果.
| M/kg | C/(N·s·m-1) | K/(N·m-1) | KF/(N·A-1) | Kui/(A·V-1) |
| 0.82 | 77.60 | 96.51 | 32.36 | 0.5 |
|
| 图 1 仿真系统框图 Fig. 1 Block diagram of simulation system |
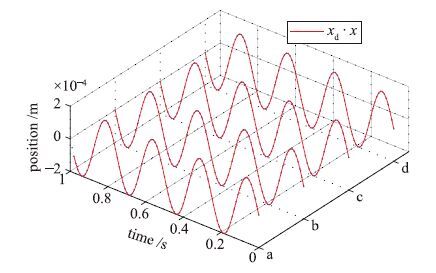
图 2给出两种控制方法分别在参数匹配情况与参数失配情况下的轨迹跟踪控制结果(图中曲线a为参数匹配情况下AAWSMC方法的结果,曲线b为参数匹配情况下ANSC方法的结果,曲线c为参数失配情况下AAWSMC方法的结果,曲线d为参数失配情况下ANSC方法的结果). 由图可知,由于自适应律的存在,两种情况下两种方法都能基本上完成轨迹跟踪.
|
| 图 2 位置跟踪结果(实验1) Fig. 2 Results of position tracking control(expt.1) |
通过图 3给出的两种控制方法的位置跟踪误差对比(其中: 图 3(a)、 3(b)分别是两种情况下AAWSMC方法的位置跟踪误差及控制输入,图 3(c)、 3(d)分别是两种情况下ANSC方法的位置跟踪误差及控制输入). 进一步对比跟踪控制效果: 无论名义参数与实际参数是否存在偏差,当不存在外部扰动时(0.5 s前),两种方法的位置跟踪误差都远小于1×10-6 m; 当外部扰动存在时(0.5 s后),两种方法的位置跟踪误差明显增大. 对比可知: AAWSMC方法跟踪误差相对较大(参数匹配情况下稳定后跟踪误差峰峰值约为2×10-6 m,参数失配情况下稳定后误差峰峰值约为3×10-6 m),而ANSC方法的最大跟踪误差约为1×10-6 m,大约0.005 s后跟踪误差稳定,参数匹配情况与参数失配情况下误差峰峰值都小于0.24×10-6 m. 由此可知: 两种方法对参数不确定性都具有较好的鲁棒性,但是AAWSMC的自适应能力及切换控制增益有限,因此对外部扰动的抑止效果不佳,而本文的ANSC方法的补偿效果较好(稳定后误差峰峰值为AAWSMC方法的24%),但是由于忽略了外部扰动的时变性,无法实现完美补偿.
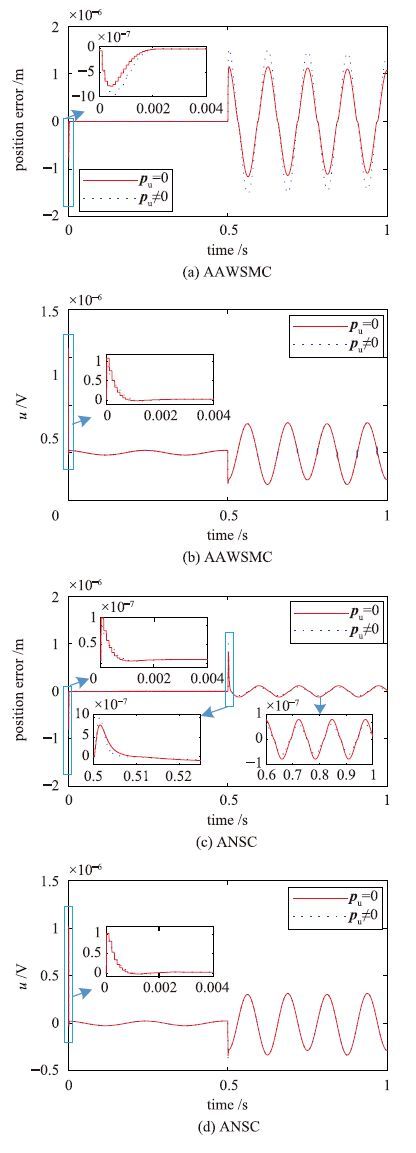
|
| 图 3 位置跟踪误差及控制输入对比(实验1) Fig. 3 Comparison of position error and control input (expt.1) |
注2 尽管AAWSMC方法设计时未考虑运动质量偏差,但是当外部扰动较小时,运动质量偏差所造成的影响可以等效为其他参数偏差(等效阻尼系数、 等效刚度等)影响的组合,同时在切换项的帮助下,可以达到较好的控制品质(图 2(a)中0.5 s前,位置跟踪误差远小于1×10-6 m).
图 4给出系统启动阶段(0~0.004 s)跟踪误差对比. 通过放大可知: 无论参数匹配情况还是参数失配情况,ANSC方法的位置跟踪误差收敛速度都要略快于AAWSMC方法(以误差收敛到0.1×10-6 m范围内为标准,参数匹配情况下AAWSMC和ANSC方法分别需要0.001 54 s、 0.001 50 s,参数失配情况下AAWSMC和ANSC方法分别需要0.001 58 s、 0.001 52 s).
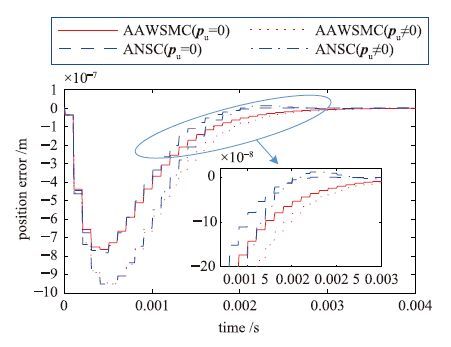
|
| 图 4 启动阶段位置跟踪误差对比(实验1) Fig. 4 Comparison of position error in the start-up phase (expt.1) |
图 5给出了电机控制输入的对比. 当外部扰动为0时,AAWSMC方法的切换控制部分较弱,控制输入较为平滑; 外部扰动加入后,当自适应补偿不够充分时,切换控制部分随即增强,控制输入出现明显的“抖颤”现象(图 5中圈内),从而改善控制品质(实际系统中难以实现,并且可能引起系统的不稳定). 而本文给出的ANSC方法,对外部扰动具有较好的自适应能力,控制输入平滑连续,不存在“抖颤”现象.
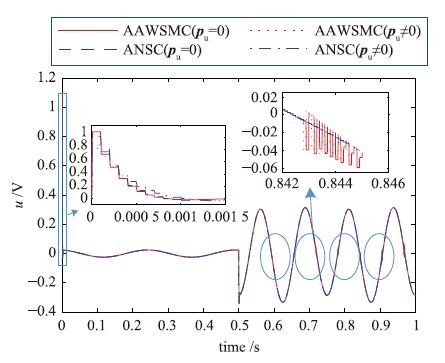
|
| 图 5 控制输入对比(实验1) Fig. 5 Comparison of control input (expt.1) |
图 6给出本文提出的ANSC方法在控制过程中,算法对不确定参数的估计结果. 可以看出估计结果并不会收敛,该现象符合第3节中的分析,即: 所提出的ANSC方法无法保证参数估计值趋于真实值,但能够保证跟踪误差趋于0. 研究表明,只有输入信号满足持续激励条件时估计值才会逼近真值,而实际系统则无法保证[19, 20]. 因此,所提出方法选择投影式自适应律来避免估计值发散影响控制.
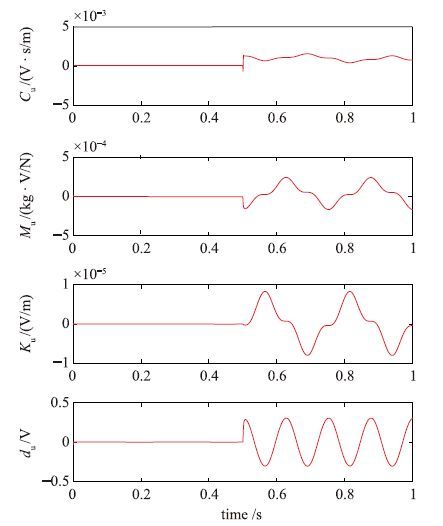
|
| 图 6 参数估计值(实验1) Fig. 6 Estimation result of parameters (expt.1) |
为进一步考察所提出方法中的分数幂次对控制的影响,设计实验2: 选择α=0.9、 α=1,重复参数失配情况下的仿真实验(其他参数不变,具体参数见上文),并将结果与α=0.75时及AAWSMC方法进行对比. 图 7给出了位置跟踪误差对比,图 8给出控制输入对比. 由跟踪误差对比可知,稳定后跟踪误差方面: 当无外部扰动时(0.5 s前),4个实验的稳定后跟踪误差都远小于1×10-6 m; 当外部扰动加入后(0.5 s后),稳定后跟踪误差峰峰值分别为3×10-6 m(AAWSMC)、 0.189×10-6 m(ANSC,α=0.75)、 0.64×10-6 m(ANSC,α=0.9)、 2.79×10-6 m(ANSC,α=1). 可以看出当α=0.75时,稳定后跟踪误差最小,α越大则误差越大. 跟踪误差收敛速度方面,启动阶段(0~0.006 s,图 7左侧放大图)跟踪误差收敛到0.5×10-6 m内时间分别为0.001 1 s(AAWSMC)、 0.001 05 s(ANSC,α=0.75)、 0.002 7 s(ANSC,α=0.9)、 0.009 5 s(ANSC,α=1),由上述数据可知,α=0.75时ANSC方法的跟踪误差收敛速度略优于AAWSMC(若取更小的误差范围,收敛速度方面的优势更明显),此外α越大ANSC方法的跟踪误差收敛过程越慢(α=0.9时收敛时间是α=0.75时的一倍多,当α=1时收敛时间达到α=0.75时的9倍多); 在外部扰动初始加入阶段(0.5~0.51 s图 7右侧放大图),最大误差分别为1.53×10-6 m(AAWSMC)、 1×10-6 m(ANSC,α=0.75)、 2.62×10-6 m(ANSC,α=0.9)、 5.5×10-6 m(ANSC,α=1),对比可知: 相同外部扰动下,α=0.75时ANSC的最大误差最小,其他3个实验的最大误差分别为其1.5倍(AAWSMC),2.62倍(ANSC,α=0.9)、 5.5倍(ANSC,α=1); 跟踪误差收敛到稳定的时间分别为0.003 s(AAWSMC)、 0.004 5 s(ANSC,α=0.75)、 0.005 1 s(ANSC,α=0.9)、0.005 5 s(ANSC,α=1),显然综合考虑收敛时间与稳定后误差峰峰值,α=0.75时ANSC方法性能最佳. 综上可知: 相同控制增益下,调节ANSC方法中的分数幂次项可以有效改善系统的收敛速度及鲁棒性(主要体现在稳定后收敛误差峰峰值),理论上α越小跟踪误差及过渡时间越小,但α无限小是不实际的,因为实际应用中α过小可能会引起系统“抖颤”.
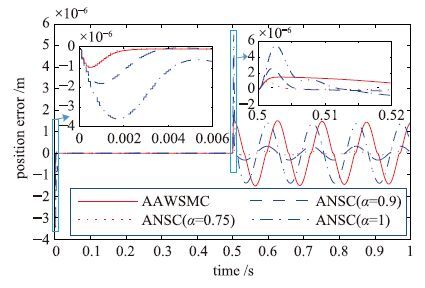
|
| 图 7 位置跟踪误差对比(实验2) Fig. 7 Comparison of position error(expt.2) |
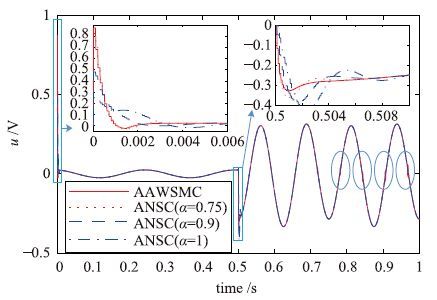
|
| 图 8 控制输入对比(实验2) Fig. 8 Comparison of control input (expt.2) |
由图 8给出的控制输入对比可以看出,ANSC方法在控制过程中控制输入平滑,没有出现AAWSMC方法中存在的“抖颤”现象.
注3 实际上当α=1时,本文所设计的控制方法退化为普通的自适应PD控制.
5 结论针对音圈电机伺服系统轨迹跟踪控制品质受到模型不确定性(包括动力学参数及外部负载扰动)影响的问题展开研究. 建立参数不确定形式的动力学模型,设计了一种自适应非光滑控制方法,将自适应与非光滑控制相结合,采用自适应律补偿模型不确定性影响,结合非光滑控制提高闭环系统收敛速度及鲁棒性. 通过仿真及对比验证本文方法的有效性,结果表明,本文所设计的自适应非光滑控制方法具有自适应能力,能改善轨迹跟踪控制品质,算法简单,易于实现,无需准确的系统参数,适合应用于复杂工况及存在高控制精度要求的音圈电机伺服系统.
| [1] | 刘红忠, 丁玉成, 李涤尘, 等. 多维微驱动器纳米定位系统的研究[J]. 信息与控制, 2002, 31(5): 446-450. Liu H Z, Ding Y C, Li D C, et al. Submicro-positioning system based on multi-dimensional ultraprecise micro actuators[J]. Information and Control, 2002, 31(5): 446-450. |
| [2] | Yu H C, Lee T Y, Wang S J, et al. Design of a voice coil motor used in the focusing system of a digital video camera[J]. IEEE Transactions on Magnetics, 2005, 41(10): 3979-3981. |
| [3] | 赵兴玉, 张胜泉, 张大卫. 基于音圈电机精密定位平台的控制系统设计与仿真[J]. 天津大学学报, 2007, 40(2): 127-132. Zhao X Y, Zhang S Q, Zhang D W. Design and simulation of the control system of precision positioning table driven by voice coil actuator[J]. Journal of Tianjin University, 2007, 40(2): 127-132. |
| [4] | Liu Y, Zhang M, Zhu Y, et al. Optimization of voice coil motor to enhance dynamic response based on an improved magnetic equivalent circuit model[J]. IEEE Transactions on Magnetics, 2011, 47(9): 2247-2251. |
| [5] | 郝齐, 关立文, 王立平. 基于遗传算法并联机床电机伺服系统控制参数整定[J]. 清华大学学报: 自然科学版, 2010, 50(11): 1801-1806. Hao Q, Guan L W, Wang L P. GA-based control parameter tuning of parallel machine tool motor servo systems[J]. Journal of Tsinghua University: Science and Technology, 2010, 50(11): 1801-1806. |
| [6] | Yao B, Li X. Adaptive robust motion control of linear motors for precision manufacturing[J]. Mechatronics, 2002, 12(4): 595-616. |
| [7] | Li X, Yao B. Adaptive robust precision motion control of linear motors with negligible electrical dynamics: theory and experiments[J]. IEEE Transactions on Mechatronics, 2001, 6(4): 444-452. |
| [8] | 张国柱, 陈杰, 李志平. 基于复合自适应律的直线电机自适应鲁棒控制[J]. 控制理论与应用, 2009, 26(8): 833-837. Zhang G Z, Chen J, Li Z P. An adaptive robust control for linear motors based on composite adaptation[J]. Control Theory & Applications, 2009, 26(8): 833-837. |
| [9] | 曹荣敏, 侯忠生. 直线电机的非参数模型直接自适应预测控制[J]. 控制理论与应用, 2008, 25(3): 587-590. Cao R M, Hou Z S. Nonparametric model direct adaptive predictive control for linear motor[J]. Control Theory & Applications, 2008, 25(3): 587-590. |
| [10] | 王大彧, 郭宏. 基于扩张状态观测器的直驱阀用音圈电机控制系统[J]. 中国电机工程学报, 2011, 31(9): 88-93. Wang D Y, Guo H. An extended state observer based control system of voice coil motor used in direct drive valve[J]. Proceedings of the CSEE, 2011, 31(9): 88-93. |
| [11] | Lin C M, Li H Y. Adaptive dynamic sliding-mode fuzzy CMAC for voice coil motor using asymmetric Gaussian membership function[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5662-5671. |
| [12] | 张扬名, 闫鹏. 线性电机伺服系统的自适应鲁棒控制[J]. 控制理论与应用, 2015, 32(3): 287-294. Zhang Y M, Yan P. Adaptive robust control for linear motor servo systems[J]. Control Theory & Applications, 2015, 32(3): 287-294. |
| [13] | Bhat S P, Bernstein D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766. |
| [14] | 李世华, 丁世宏, 田玉平. 一类二阶非线性系统的有限时间状态反馈镇定方法[J]. 自动化学报, 2007, 33(1): 101-104. Li S H, Ding S H, Tian Y P. A finite-time state feedback stabilization method for a class of second order nonlinear systems[J]. Acta Automatica Sinica, 2007, 33(1): 101-104. |
| [15] | 丁世宏. 非线性系统的有限时间控制若干问题研究[D]. 南京: 东南大学, 2010. Ding S H. Research on some finite-time control problems for nonlinear systems[D]. Nanjing: Southeast University, 2010. |
| [16] | 李世华, 丁世宏, 都海波, 等. 非光滑控制理论与应用[M]. 北京: 科学出版社, 2013. Li S H, Ding S H, Du H B, et al. Nonsmooth control theory and application[M]. Beijing: Science Press, 2013. |
| [17] | Yao B, Tomizuka M. Smooth robust adaptive sliding mode control of manipulators with guaranteed transient performance[J]. Journal of Dynamic Systems, Measurement and Control, 1996, 118(4): 764-775. |
| [18] | Hou M, Duan G, Guo M. New versions of Barbalat's lemma with applications[J]. Journal of Control Theory and Applications, 2010, 8(4): 545-547. |
| [19] | Khalil H K, Grizzle J W. Nonlinear systems (Vol.3)[M]. Upper Saddle River, NJ, USA: Prentice Hall, 1996. |
| [20] | 斯洛坦, 李卫平. 程代展, 译. 应用非线性控制[M]. 北京: 机械工业出版社, 2006. Slotine J E, Li W P. Cheng D Z, trans. Applied nonlinear control[M]. Beijing: China Machine Press, 2006. |



