1 引言
迭代学习控制主要是针对有限时间上具有重复操作特征的控制系统,通过综合以往获得的信息和控制输入来不断修正下一次的控制输入,使得控制器的迭代过程具有自学习的能力,最终达到期望的控制效果[1-6].
传统迭代学习控制算法通常在给出收敛性条件的同时给出学习增益的取值范围,但是凭经验所选取的学习增益容易存在迭代跟踪误差非单调收敛或误差收敛后发散的现象. 为克服这种盲目性取值,引入相关性能指标函数进行优化. 如Ratcliffe等针对离散线性系统提出基于误差优化指标的迭代学习控制算法,采用最速下降法得到最优化的控制律[7]. Amann等针对离散反馈前馈线性系统,在性能指标中引入控制项进行优化目标[8]. Xu等针对离散线性系统输出受约束被控系统,提出了基于凸优化的范数优化理论[9].
但在实际的控制系统设计中,确定性模型往往不可精确获取,必须对不确定性模型进行算法研究和优化. 文[10]提出一种PID非线性学习控制器,通过建立群粒子优化算法寻找最优的PID参数,但上述算法没有考虑系统受到实际不确定性因素的影响. 文[11]将范数最优化迭代学习算法应用到非线性系统跟踪问题,通过遗传算法求解目标函数得到下一次的更新控制信号,该算法能够以几何速度收敛至0. 文[12]主要是针对非线性离散系统进行数据驱动终端迭代学习控制. 文[13]针对线性系统参数存在扰动的情况下给出一种P型闭环迭代学习控制算法. 文[14]仅对存在扰动非线性系统给出了鲁棒性控制算法. 文[15]提出离散非线性系统的参数指标优化方案. 但这些方法对于不确定性的模型要求都具有严格限制,且都要求迭代初值严格一致,实际应用效果一般.
因此,本文针对一类带有干扰的离散非线性系统,提出一种P型开闭环的迭代学习控制算法,并将依据最优控制理论构建的性能指标引入到迭代控制算法中,进而对扰动情形下迭代控制算法中的相关增益参数进行最优化,并通过λ范数证明了存在干扰和初值不严格一致时系统的鲁棒收敛性,且对优化后控制律跟踪误差的单调收敛性进行了证明. 最后将该算法应用到移动机器人控制系统验证算法的有效性.
2 问题描述考虑第k次重复运行的离散非线性系统:

|
(1) |
式中,0≤t≤T,xk(t)∈Rn,uk(t)∈Rr,yk(t)∈Rm分别为系统运行时第k次状态量、 控制输入量、 输出量; ωk(t)∈Rn,vk(t)∈Rm分别为系统运行时的第k次状态和输出干扰量,且对于任意的k>0,t∈{0,1,…,T},必然有||ωk(t)||≤bω,vk(t)≤bv. f(t,xk(t))和B(t,xk(t))为系统第k次运行时的非线性系统矩阵函数,且f(·)、 B(·)关于x满足一致全局Lipschitz条件,函数g(t,xk(t))存在x的偏导数,且满足上确界要求:
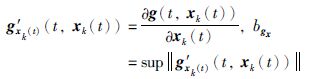
|
在不注明的情况下,g′xk(t)(t,xk(t))均简写为g′xk(t).
考虑到重复运行系统(1)各个批次的初始状态不同,假设对于任意批次k>0,t∈{0,1,…,T},必然存在bx0>0,使得系统的初态满足||xd(0)-xk(0)||≤bx0.
针对非线性系统(1)设计P型开闭环迭代学习控制律:
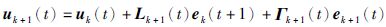
|
(2) |
其中,Lk+1(t)、 Γk+1(t)为迭代增益矩阵,且实际控制器增益有界,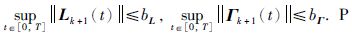
|
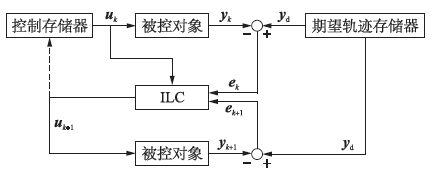
| 图 1 P型开闭环控制结构图 Figure 1 Structure diagram of P-type open-closed control |
定义[16] 向量函数h∶{0,1,…,T}→Rn的λ范数定义为:
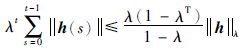
|
(3) |
定理 1 针对离散非线性系统(1),采用如式(2)所示的迭代学习控制律,若系统满足条件||I-Lk+1(t)g′k(t+1)B(t,xk(t))||<1,则该非线性离散系统具有严格的鲁棒稳定性. 特别当bω→0,bv→0,bx0→0时,系统输出yk(t)能稳定跟踪参考输入yd(t).
证明 定义输出跟踪误差ek(t)=yd(t)-yk(t),令:

|
(4) |

|
(5) |
则由式(2)和式(4)得到:

|
(6) |
其中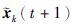
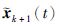

|
(7) |
进一步将式(7)代入式(6),并取范数后可以得到:

|
(8) |
对式(7)两端取范数后可得:
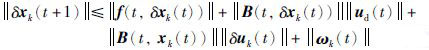
|
(9) |
令
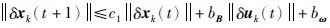
|
(10) |
其中c1=kfkBbud,进而可得:
其中c1=kf+kBbud,进而可得:
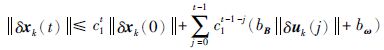
|
(11) |
令: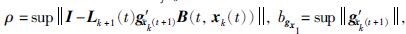
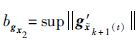
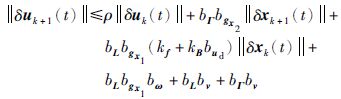
|
(12) |
接下来,将式(11)代入式(12)中,并令c3=bΓbgx2,c2=bLbgx1(kf+kBbud),c4=bLbgx1bω+bLbv+bΓbv,则:
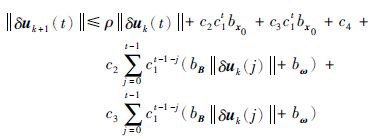
|
(13) |
接下来对式(13)两端同乘以λt,并取λ范数立即可得:
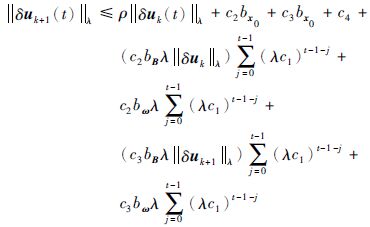
|
(14) |
对式(14)进行整理:
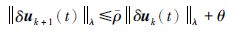
|
(15) |
其中:

|
(16) |
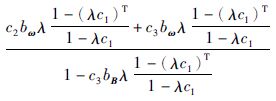
|
(17) |
即经k次迭代后:
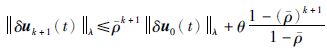
|
(18) |
当λ取足够小,
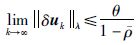
|
(19) |
同理,对式(11)两边同乘以λt,并取范数得:
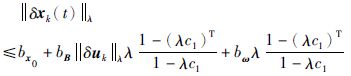
|
(20) |
由于
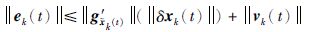
|
(21) |
将式(11)代入式(21),两端乘以λt,并取λ范数得到:
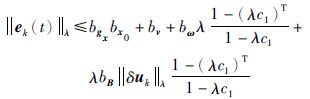
|
(22) |
而且将式(19)代入式(22)中,进一步可得:

|
(23) |
通过k次迭代,则最终误差会收敛到一定范围以内,即: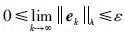

|
(24) |
特别地,当非线性系统不存在外界因素的干扰且系统初始值与给定期望初态严格一致时,limk→∞ekλ=0,则定理1同样适用于确定性系统.
4 算法优化虽然定理1条件使得系统满足稳定性条件,但稳定参数的选择范围较大,稳定参数的人为随意选择将使得系统即使满足稳定性条件通常也会降低最终控制性能. 因此进一步考虑存在干扰因素的非线性离散系统(1),对其进行算法优化,其中t∈{0,1,…,T}为采样时刻,输出表示为

|
则输出误差可表示为
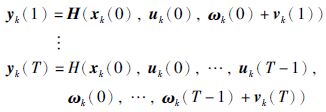
|
(25) |
由微分中值定理及非线性系统可得:
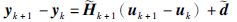
|
(26) |
其中,
为方便求解,将增益矩阵改写成一种特殊形式: Lk+1=αk+1W,Γk+1=βk+1M,其中W,M分别为与Lk+1和Γk+1相同结构和维数的构造矩阵,αk+1、 βk+1分别为参量,则迭代学习控制律可写成:
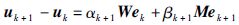
|
(27) |
得到ek+1,即ek+1=ek-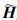
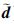
整理得到:

|
(28) |
考虑性能指标:
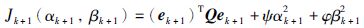
|
(29) |
其中调节量ψ>0,φ>0,Q=I.
利用最优控制原理[17]中极值原理可以得到:
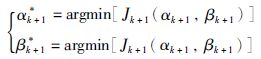
|
(30) |
注意到这里求出的αk+1*与βk+1*分别含有ψ和φ,说明ψ与φ对αk+1取最优解具有调节作用,同时对βk+1也具有调节作用,因此需对ψ和φ求偏导得到其相应的最优解,即:
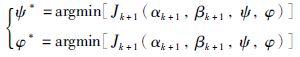
|
(31) |
综合定理1中约束条件建立多目标优化函数[18],得到最优化参数αk+1*,βk+1*,代入迭代学习律中即可得优化控制器.
定理 2 在满足定理1的约束条件下,由式(29)所示的优化性能指标,求解式(30)和式(31)得到的参数优化迭代学习控制律(27)作用于离散非线性系统(1)时,系统的输出轨迹跟踪误差单调收敛.
证明 对优化的单调收敛迭代学习控制律,由式(29)得到:
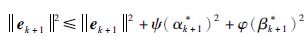
|
(32) |
当取非最优化解αk+1=0,βk+1=0,则:
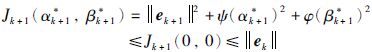
|
(33) |
因此,||ek+1||≤||ek||,即误差单调收敛,ek+1的极限必然存在. 根据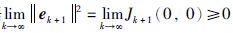
实际上,对于确定性系统,由于
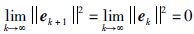
综合式(32)和式(33)可得:
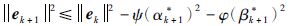
|
(34) |
经k次迭代有:
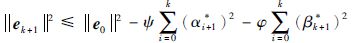
|
(35) |
实际上在理想状态下,系统不存在干扰,且初值严格一致的条件下[7],对于P型开环的参数优化式(35)中
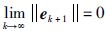
移动机器人运动模型[19-20]如图 2所示,在同一根轴上有两个独立的推进轮,机器人在二维空间移动,点z(t)代表机器人的当前位置,z(t)点在广义坐标中定义为[sz(t),pz(t),θz(t)],sz(t)和pz(t)为直角坐标系下z(t)的坐标,θz(t)为机器人的方位角. 当机器人的标定方向为地理坐标系的横轴正半轴时,θz(t)定义为0. 移动机器人受不完全约束的影响而只能在驱动轮轴的方向运动,点z(t)的线速度和角速度定义为z(t)和z(t).

|
| 图 2 移动机器人运动模型 Figure 2 Mobile robot motion model |
针对z(t)点,移动机器人的离散运动学方程可描述为
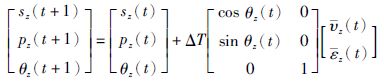
|
其中,ΔT为采样时间,状态向量x(t)=[sz(t),pz(t),θz(t)]T,速度向量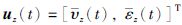
采用如式(2)所示的迭代学习控制律,期望位置轨迹sd(t)=cos(πt),pd(t)=sin(πt),θd(t)=πt+π/2,采样时间ΔT=0.001 s. 根据定理1的收敛条件及优化算法,取
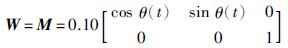
|
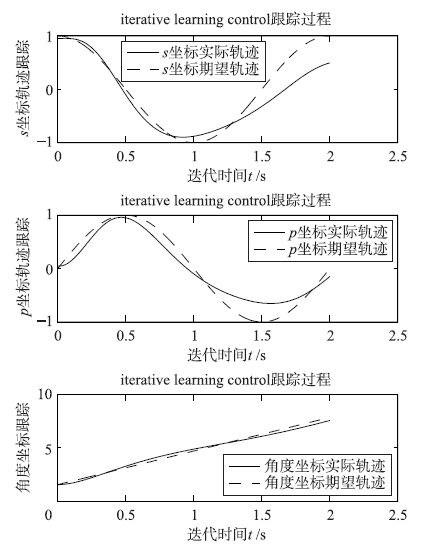
给定最大跟踪误差精度为εmax≤0.06(后面为便于误差数据对比,在误差精度小于0.06时继续迭代,直到达到允许最大迭代次数n=50). 当初始状态取s0=0.95,p0=0.05,θ0=π/2,此时与期望初值不严格一致,且状态和输出存在扰动的情况下,实际轨迹跟踪曲线分别如图 3和图 4所示,输出误差曲线如图 5所示. 对移动机器人控制系统进行增益矩阵参数优化,根据定理2的优化算法及定理1的约束条件取参数α*=0.01,β*=16,则根据优化迭代学习控制器得到的轨迹跟踪曲线分别如图 6和图 7所示,输出误差曲线如图 8所示.
|
| 图 3 传统控制方法下的跟踪曲线与期望曲线 Figure 3 The curve of tracking and desired using traditional method |
|
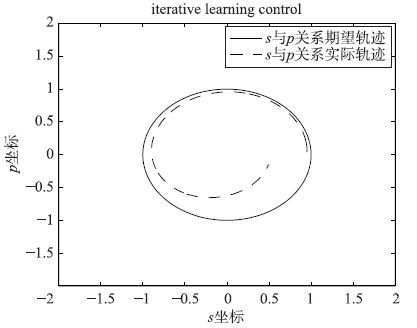
| 图 4 >传统控制方法下移动机器人的运动曲线 Figure 4 The motion curve of mobile robot using traditional method |
|
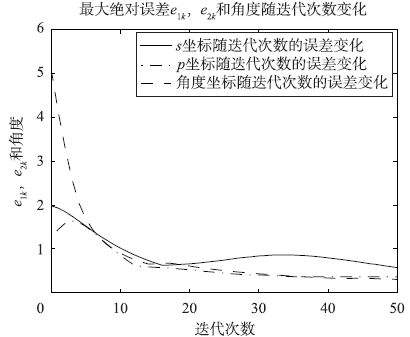
| 图 5 传统方法下的迭代次数与最大绝对跟踪误差曲线 Figure 5 The curve of the number of iterations and the maxmum absolute error using traditional method |

|
| 图 6 优化方法下的跟踪曲线与期望曲线 Figure 6 The curve of tracking and desired using optimal method |

|
| 图 7 优化方法下移动机器人的运动曲线 Figure 7 The motion curve of mobile robot using optimal method |
|
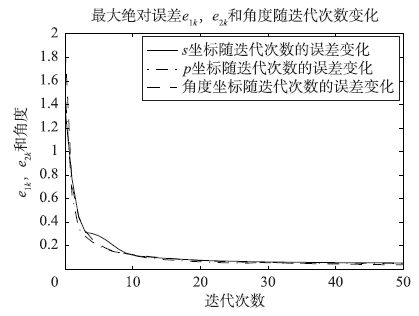
| 图 8 优化方法下的迭代次数与最大绝对跟踪误差曲线 Figure 8 The curve of the number of iterations and the maxmum absolute error using optimal method |
由图 4和图 7对比可知,优化后移动机器人的跟踪精度明显改善,扰动情形下的跟踪曲线基本达到期望曲线轨迹,并将图 5和图 8对比可知,优化后的跟踪误差严格单调收敛,且优化后的收敛速度明显加快. 由表 1中误差数据对比可以直观地发现,经优化后的跟踪控制效果明显得到改善,优化后经迭代30次基本就能达到较好的收敛效果和误差精度.
| 迭代次数k | 传统方法最大绝对误差数据 | 优化最大绝对误差数据 | ||||
| e1k | e2k | e3k | e1k | e2k | e3k | |
| 1 | 1.981 7 | 1.263 6 | 5.095 3 | 1.353 5 | 1.493 0 | 1.852 8 |
| 5 | 1.635 4 | 1.602 8 | 2.048 0 | 0.306 5 | 0.233 5 | 0.256 2 |
| 10 | 1.105 4 | 0.979 4 | 0.993 4 | 0.137 1 | 0.132 6 | 0.134 7 |
| 15 | 0.734 7 | 0.586 1 | 0.655 5 | 0.097 4 | 0.087 1 | 0.099 6 |
| 20 | 0.645 5 | 0.532 4 | 0.631 7 | 0.080 9 | 0.068 0 | 0.079 3 |
| 25 | 0.726 7 | 0.459 3 | 0.520 3 | 0.071 5 | 0.056 4 | 0.066 3 |
| 30 | 0.819 8 | 0.402 3 | 0.443 2 | 0.064 7 | 0.057 1 | 0.057 7 |
| 40 | 0.813 5 | 0.360 0 | 0.340 8 | 0.058 8 | 0.052 8 | 0.047 2 |
| 50 | 0.593 2 | 0.362 4 | 0.306 0 | 0.055 8 | 0.051 7 | 0.040 4 |
本文以受扰非线性离散系统为研究对象,提出P型开闭环迭代学习控制律,讨论其鲁棒收敛性问题,通过对迭代学习控制律参数进行优化,提高了收敛速度和跟踪精度,验证了跟踪误差单调收敛性问题. 最后将算法应用到二维运动移动机器人控制系统上进行仿真,验证了算法的有效性. 本文算法将可进一步推广应用于注塑成型、 生物发酵等间歇过程.
| [1] | Wang H B, Wang Y. Iterative learning control for nonlinear systems with uncertain state delay and arbitrary initial error[J]. Control Theory and Application , 2011, 9 (4) : 541–547. DOI:10.1007/s11768-011-9235-y |
| [2] | Yin C K, Xu J X, Hou Z S. On iterative learning control design for tracking iteration-varying trajectories with hign-order internal model[J]. Control Theory and Application , 2010, 8 (3) : 309–306. DOI:10.1007/s11768-010-0019-6 |
| [3] | 齐丽强, 孙明轩, 管海娃. 非参数不确定系统的有限时间迭代学习控制[J]. 自动化学报 , 2014, 40 (7) : 1320–1324. Qi L Q, Sun M X, Guan H W. Finite-time iterative learning control for systems with nonparametric uncertainties[J]. Acta Automatica Sinica , 2014, 40 (7) : 1320–1324. |
| [4] | Arimoto S, Kawamuar S, Miyazaki F. Bettering operating operation of robots by learning[J]. Journal of Robotic Systems , 1984, 1 (1) : 123–140. |
| [5] | 陶洪峰, 丁保, 杨慧中. 非线性系统迭代跟踪控制的批次遗忘学习算法[J]. 信息与控制 , 2011, 40 (6) : 772–776. Tao H F, Ding B, Yang H Z. Forgetting learning algorithm with batches for iterative tracking control of nonlinear systems[J]. Information and Control , 2011, 40 (6) : 772–776. |
| [6] | 陶洪峰, 霰学会, 杨慧中. 输入饱和非线性系统的周期自适应补偿学习控制[J]. 自动化学报 , 2014, 40 (9) : 1998–2004. Tao H F, Xian X H, Yang H Z. Periodic adaptive compensating learning control of nonlinear systems with saturated input[J]. Acta Automatica Sinica , 2014, 40 (9) : 1998–2004. |
| [7] | Ratcliffe J D, Hatonen J J, Owens D H, et al. Robustness analysis of an adjoint optimal iterative learning controller with experimental verification[J]. Intternational Journal of Robust Nonlinear Control , 2008, 18 (10) : 1089–1113. DOI:10.1002/(ISSN)1099-1239 |
| [8] | Amann N, Owens D H, Rogers E. Iterative learning control for discrete time systems using optimal feedback and feedforward action[C]//Proceedings of the 34th Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 1995: 1696-1701. |
| [9] | Xu J, Wang Z W, Kwong R. Convex optimization based iterative learning control for iteration-varying systems under output constraints[C]//2014 11th IEEE International Conference on Control and Automation. Piscataway, NJ, USA: IEEE, 2014: 1444-1448. |
| [10] | Lin C M, Li M C, Ting A B, et al. A robust self-learning PID control system design for nonlinear systems using a particle swarm optimization algorithm[J]. International Journal of Machine Learning and Cybernetics , 2011, 2 (4) : 225–234. DOI:10.1007/s13042-011-0021-4 |
| [11] | Hatzikos V, Hatonen J, Owens D H. Genetic algorithms in norm-optimal linear and non-linear iterative learning control[J]. International Journal of Control , 2004, 77 (2) : 188–197. DOI:10.1080/00207170310001649351 |
| [12] | Chi R H, Liu Y, Hou Z S, et al. A data-driven terminal iterative learning control for nonlinear discrete-time systems[C]//Proceeding of the 11th World Congress on Intelligent Control and Automation. Piscataway, NJ, USA: IEEE, 2014: 1974-1978. |
| [13] | Dai X S, Tian S P, Peng Y J, et al. Closed loop P-type iterative learning control of uncertain linear distributed parameter systems[J]. IEEE/CAA Journal of Automatica Sinica , 2014, 1 (3) : 267–273. DOI:10.1109/JAS.2014.7004684 |
| [14] | Bu X H, Yu F S, Hou Z S, et al. Robust iterative learning control for nonlinear systems with measurement disturbaces[J]. Journal of Systems Engineering and Electronics , 2012, 23 (6) : 906–913. DOI:10.1109/JSEE.2012.00111 |
| [15] | 逄勃, 邵诚. 基于奇异值分解的PID型参数优化迭代学习控制算法[J]. 信息与控制 , 2014, 43 (4) : 483–489. Pang B, Shao C. PID-type parameter optimal iterative learning control algorithm based on singular value decomposition[J]. Information and Control , 2014, 43 (4) : 483–489. |
| [16] | 谢胜利, 田森平, 谢振东. 迭代学习控制理论与应用[M]. 北京: 科学出版社 ,2005 : 135 -138. Xie S L, Tian S P, Xie Z D. Iterative learning control theory and applications[M]. Beijing: Science Press , 2005 : 135 -138. |
| [17] | 胡寿松, 王执铨, 胡维礼. 最优控制理论与系统[M]. 北京: 科学出版社 ,2005 : 77 -87. Hu S S, Wang Z Q, Hu W L. Optimal control theory and system[M]. Beijing: Science Press , 2005 : 77 -87. |
| [18] | Wang C, Li L J. Multi-objective optimization of ethylbenzene dehydrogenation process based on modified particle swarm algorithm[J]. Control and Instrument in Chemical Industry , 2012, 39 (3) : 356–359. |
| [19] | 裴九芳, 王海, 许德章. 基于迭代学习控制的移动机器人轨迹跟踪控制[J]. 计算机工程与应用 , 2012, 48 (9) : 222–225. Pei J F, Wang H, Xu D Z. Tracking control of mobile robot based on iterative learning control[J]. Computer Engineering and Application , 2012, 48 (9) : 222–225. |
| [20] | 刘国荣, 张扬名. 移动机器人轨迹跟踪的模糊PID-P型迭代学习控制[J]. 电子学报 , 2013, 41 (8) : 1536–1541. Liu G R, Zhang Y M. Trajectory tracking of mobile robots based on fuzzy PID-P type iterative learning control[J]. Acta Electronica Sinica , 2013, 41 (8) : 1536–1541. |



