2. 中北大学电子测试技术国家重点实验室, 山西 太原 0300511
2. Nation Key Laboratory of Electronic Testing, North University of China, Taiyuan 030051
1 引言
多智能体系统的分布式协同控制已成为近年来国际控制领域研究的热点课题[1-2]. 多智能体协同控制在科学工程领域中具有广泛的应用潜力,诸如无人驾驶飞机的协调控制、 多机器人的编队控制等[3]. 目前,学界在多智能体系统分布式协同控制方面的研究主要包括编队问题[4-5]、 一致性问题[6-8]、 群集问题[9-10].
近年来,伴随着多个领导者在多智能体系统中的出现,能驱使子智能体中的跟随者进入领导者形成的特定几何空间的包容控制开始获得广大学者的关注[11-16]. 文[11]针对一类离散时间多智能体模型,采用预测控制策略,解决了其包容控制问题. 但是文[11]中的结论不能直接运用到连续时间多智能体系统中. 文[12-13]考虑了具有周期采样二阶连续时间多智能体系统的包容控制问题. 文[14]在时变无向通讯拓扑下,研究了多智能体的包容控制问题. 文[16]在切换拓扑结构下,研究了一类二阶多智能体系统的包容控制问题. 以上文献在研究多智能体系统包容控制问题时,均未涉及通讯时延. 但是,由于传输网络带宽的有限,子智能体之间进行通讯时,不可避免地存在时延. 目前,对多智能体系统进行包围控制器设计时考虑时延的成果甚为少见. 系统时延往往具备独立的分布特性,通讯时延的引入将使得多智能体系统的状态量从仅由时间单一变量决定的简单函数变成了受时延参数和时间变量共同决定的复合函数,从而增加了分析的难度. 通过对多智能体系统设计合适的包容控制器来对时延进行补偿是一项极其重要而有意义的工作.
本文考虑一类具备有界且导数有界时变时延的多智能体系统的包容控制器设计问题. 通过构造合适的Lyapunov-Krasovskii函数,根据李亚普诺夫稳定性理论和线性矩阵不等式(LMI)方法,提出了基于时滞依赖的包容控制器设计方法. 该设计能有效地驱使多智能体系统中所有跟随者的状态渐近一致性地收敛到领导者运动过程中形成的几何凸包,并通过仿真算例对该方法的有效性进行验证.
2 预备知识
令Θ=(V,ε,A)为一个权重有向图,其中V={v1,v2,…,vn}是顶点集合,ε⊆V×V是边集合,A=[aij]n×n为图Θ的权重邻接矩阵. 从顶点vj到顶点vi的一条有向边记为εji=(vi,vj),相应的邻接元素aij>0,意味着智能体vi能够接收到智能体vj的信息; 对于任一顶点vi∈V,都有aii=0. 节点vi的邻域节点集合记为Ni={vj∈V(j, i)∈ε}. 有向图Θ的拉普拉斯矩阵记为L=[lij]n×n,其中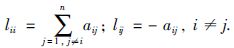
如果一个子智能体没有邻居,则称为领导者; 否则,则称为跟随者. 假设一个多智能体系统由m(m<n)个领导者和n-m个跟随者组成. 不失一般性,假设子智能体1,2,…,m为领导者,子智能体m+1,m+2,…,n为跟随者,并定义l={1,2,…,m}和f={m+1,m+2,…,n}分别表示领导者集和跟随者集. 由于领导者没有邻居,故有向图Θ对应的拉普拉斯矩阵可以分解为
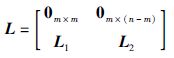
|
其中,L1∈R(n-m)×m,L2∈R(n-m)×(n-m).
接下来对于本文的通讯网络G,作出如下假设:
假设 1 通讯拓扑图G具备有向生成森林.
定义 1[17] 对于集合F,若存在x,y∈F以及λ∈[0,1]使得(1-λ)x+λy∈F成立,则称F是凸的. 此时有限点集x1,…,xn∈Rm的凸包Co{x1,…,xn}是包含所有点xi(i=1,…,n)的最小凸包. 特别地,Co{x1,…,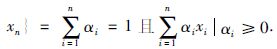
引理 12[18] 在假设1的情况下,L2所有特征值都具有正实部,-L-1L1是非负的且-L2-1L1的每一行的和为1.
3 系统模型考虑一个由m个领导者和n-m个跟随者组成的二阶多分布式智能体系统. 各子智能体的连续时间动态模型描述如下:
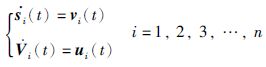
|
(1) |
其中,si(t)∈RN,vi(t)∈RN及ui(t)∈RN分别代表第i个多智能体的位置、 速度和控制输入,并用集合l={1,2,…,m}和f={m+1,m+2,…,n}分别来表示领导者集和跟随者集.
对于系统任意初始状态,若存在控制协议ui(t)使得系统(1)所有跟随者的状态渐近一致地收敛到领导者形成的凸包,则称ui(t)为多智能体系统(1)的包容控制协议. 即满足:
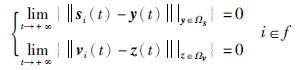
|
(2) |
其中,Ωs=Co{si(t),i∈l}及Ωv=Co{vi(t),i∈l}.
接下来,在考虑通讯时延的情况下,本文给定包容控制协议如下:
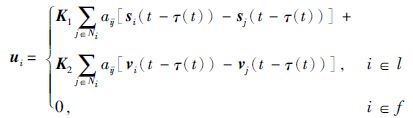
|
(3) |
其中,K=[K1,K2](K1,K2∈RN×N)是待求的包容控制增益,Ni表示第i个子智能体的邻居集,aij是图G中加权邻接矩阵的(i,j)元. τ(t)为时变通讯时延. 为了便于讨论且不是一般性,不妨假设时延τ(t)有上界η且可导,其导数有上界β,即τ(t)≤η,(t)≤β,η和β为常数.
令xi(t)=[simT(t)viT(t)]T(i=1,…,n),xl=[x1T…xT]nT,xf=[xm+1T…xT]T. 根据式(1)和式(3)可得闭环系统动态方程:
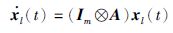
|
(4) |
和
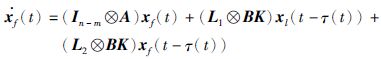
|
(5) |
其中,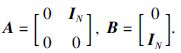
注 1 根据包容控制协议(3)可知,领导者的速度保持不变,位置是关于时间t的线性函数,可求得: si(t)=si0+vi0t(i∈l),其中,si0,vi0分别是初始位移和速度状态量,即si0=si(0),vi0=vi(0).
定义 x(t)=xf(t)+(L2-1L1⊗I2N)xl(t),由式(4)和式(5)可得
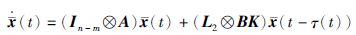
|
(6) |
注 2 由引理1可知,-L2-1L1的所有元素非负并且所有行元素的和等于1,因此可以计算出由领导者形成的凸包为(-L2-1L1⊗I2N)xl. 结合式(2)的描述可知,探讨多智能体系统(1)在协议(3)下的包容控制问题,可以等价地转化为求解满足闭环系统(6)渐近稳定的增益K.
4 包容控制器设计为了便于进一步分析含时变时延的多智能体系统包容控制器的设计方法,首先介绍如下引理:
引理 2[19] 给定正定矩阵Q∈Rm×m,常数a和b满足a<b及向量函数ν∶[a, b]→Rm可积,则下列不等式成立:
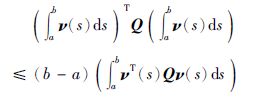
|
(7) |
引理 3[20] 给定对称矩阵
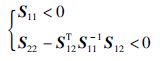
|
(8) |
或
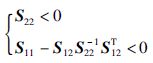
|
(9) |
定理 1 假设通讯拓扑图G具备有向生成森林. 给定常数β,η,σ<1满足σβ<1以及包容控制增益矩阵K∈RN×2N,若存在正定对称矩阵P∈R2N×2N,正定矩阵R,Q∈R2N×2N使得下列矩阵不等式成立:

|
(10) |
其中,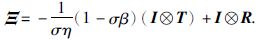
证明 首先,构造如下Lyapunov-Krasovskii函数:
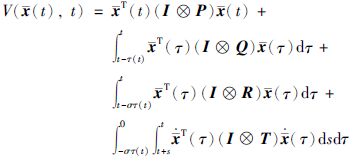
|
(11) |
显然,当P>0,Q>0,R>0,T>0时,V(x(t),t)正定. 沿着系统(6)的轨迹求函数V(x(t),t)关于时间t的导数,可得:
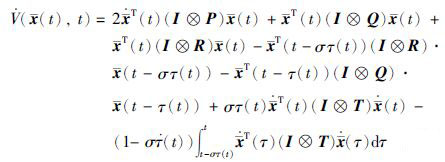
|
(12) |
由于σβ<1,根据引理2知,如下不等式成立
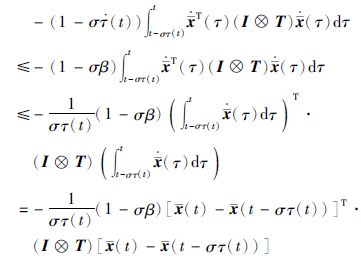
|
(13) |
将式(6)和式(13)代入式(12)中可得
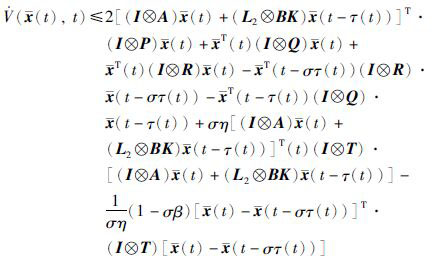
|
(14) |
令ξ=(xt)-x(t-στ(t)),φ=[xT(t),xT(t-τ(t)),ξ]T,不等式(14)可等价地写为
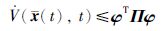
|
(15) |
其中,

|
对于线性矩阵不等式(10),应用引理3所描述的Schur补原理可知Π<0. 又根据(15)可知V·((t),t)<0,即系统(6)渐进稳定. 因此,当t→∞时,(t)=xf(t)+(L2-1L1⊗I2N)xl(t)→0,即xf(t)→-(L2-1L1⊗I2N)xl(t). 故定理1得证.
基于定理1所描述的包容控制协议存在条件,接下来将给出求解包容控制增益K的方法.
定理 2 假设通讯拓扑图G具备一个有向的生成森林. 给定常数λ>0,β,σ<1满足σβ<1,若存在正定对称矩阵X∈R2N×2N,正定矩阵,∈R2N×2N以及矩阵W. 若下列LMI成立:
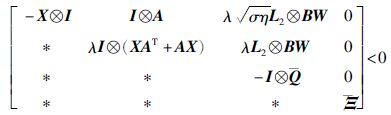
|
(16) |
其中,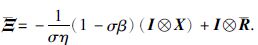
证明 定义P=λT,在不等式(10)的两边分别左乘diag{I2N(n-m),I⊗T-1,I⊗T-1,I⊗T-1}和右乘它的转置,并令T-1=X,W=KT-1,=T-1QT-T,R=T-1RT-T,便可得不等式(16),因此,定理2得证.
注 3 显然不等式(16)是线性的. 文[14-16]在不考虑时延的情况下探讨了一类分布式多智能体系统的包容控制问题,其包容控制增益是基于拉普拉斯矩阵特征给定的一个数值范围. 这里可以通过求解线性矩阵不等式(16)的可行解来直接获得满意的包容控制器参数.
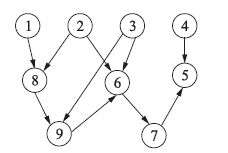
5 算例仿真为验证本文所提出的设计方法的有效性,考虑由9个智能体组成的多智能体系统,其中1-4为领导者,5-9为跟随者,对应的通信拓扑如有向图 1所示,其中相应的邻接元素都为1. 假设整个通讯过程包含时变时延τ(t),给定时延上界η=0.46,其导数上界为β=1.56,即有τ(t)<0.46,(t)<1.56. 使用Matlab, 选取参数σ=0.32,根据定理2可求得包容控制增益
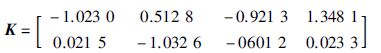
|
|
| 图 1 具有一个有向生成森林的通信拓扑G Figure 1 Digraph G which contains a directed spanning forest |
将此包容控制器参数代入式(3)所描述的控制协议并运用到多智能体系统中,可得到如图 2所示的智能体状态轨迹曲线. 从图 2可以看出,在所设计的控制协议下,跟随者的位置和速度都各自渐近地收敛到领导者运动过程中形成的凸包.
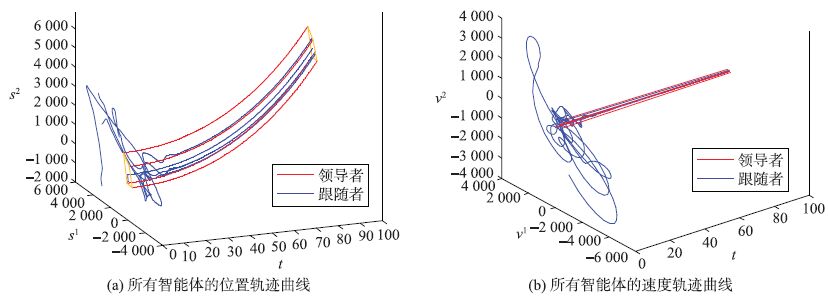
|
| 图 2 基于本文方法所有智能体的状态轨迹 Figure 2 State trajectories of all the agents based on the method in this paper |
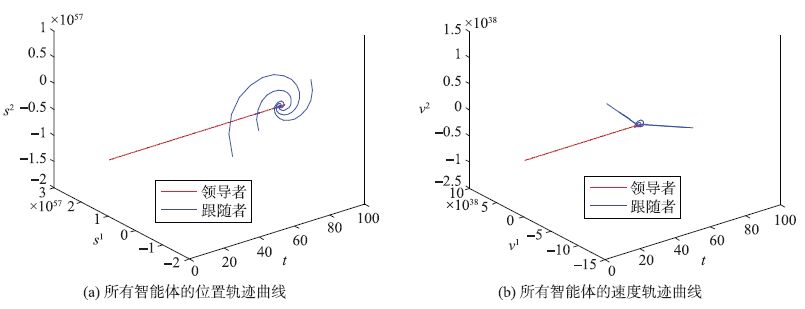
进一步,在与上述同一系统初始状态及相同时延影响下,使用文[15]中所提出的包容控制算法进行对比. 可得系统状态响应如图 3所示,由图 3可知,跟随者的位置和速度在文[15]中的协议下系统状态都是发散的. 因此,本文提出的包容控制器设计方法对多智能体系统中的时变通讯时延具有良好的补偿效果. 从而,进一步阐明了本文方法的有效性和优越性.
6 总结本文利用时延信息,针对有向网络拓扑下的时延多智能体基于时滞依赖法设计了一类的包容控制器. 结合李亚普诺夫稳定性理论和矩阵不等式(LMI)理论,推导了包容控制存在的条件,并将包容控制器的设计转化成求解线性矩阵不等式可行解的问题. 仿真实验表明,该设计能有效地驱使多智能体系统中所有跟随者的状态渐近收敛到领导者运动过程中形成的凸包.
| [1] | Ren W, Beard R W, Atkins E M. Information consensus in multivehicle cooperative control[J]. IEEE Control Systems Magazine , 2007, 27 (2) : 71–82. DOI:10.1109/MCS.2007.338264 |
| [2] | Cortes J, Bullo F. Coordination and geometric optimization via distributed dynamical systems[J]. SIAM Journal on Control and Optimization , 2003, 44 (5) : 1543–1574. |
| [3] | 吴正平, 关治洪, 吴先用. 基于一致性理论的多机器人系统队形控制[J]. 控制与决策 , 2007, 22 (11) : 1241–1244. Wu Z P, Guan Z H, Wu X Y. Consensus based formation control of multi-agent system[J]. Control and Decision , 2007, 22 (11) : 1241–1244. |
| [4] | Reynolds C W. Flocks, herds and schools: A distributed behavior model[J]. Computer Graphics , 1987, 21 (4) : 5–34. |
| [5] | Saber R O. Flocking for multi-agent dynamic systems: Algorithms and theory[J]. IEEE Transactions on Automatic Control , 2006, 51 (3) : 401–420. DOI:10.1109/TAC.2005.864190 |
| [6] | Liu S, Xie L H, Zhang H S. Distributed consensus for multi-agent systems with delays and noises in transmission channels[J]. Automatica , 2010, 47 (5) : 920–934. |
| [7] | 刘成林, 田玉平. 具有时延的多个体系统的一致性问题综述[J]. 控制与决策 , 2009, 24 (11) : 1601–1608. Liu C L, Tian Y P. Survey on consensus problem of multi-agent systems with time delays[J]. Control and Decision , 2009, 24 (11) : 1601–1608. |
| [8] | Xiao F, Wang L. Consensus protocols for discrete-time multi-agent systems with time-varying delays[J]. Automatica , 2008, 44 (10) : 2577–2582. DOI:10.1016/j.automatica.2008.02.017 |
| [9] | Saber R O. Distributed Kalman filter with embedded consensus filters[C]//Proceedings of the Joint CDC-ECC Conference. Piscataway, NJ, USA: IEEE, 2005: 8179-8184. |
| [10] | Saber R O, Shamma J S. Consensus filters for sensor networks and distributed sensor fusion[C]//Proceedings of the Joint CDC-ECC Conference. Piscataway, NJ, USA: IEEE, 2005: 6698-6703. |
| [11] | Galbusera L, Ferrari-Trecate G, Scattolini R. A hybrid model predictive control scheme for containment and distributed sensing in multi-agent systems[J]. Systems & Control Letters , 2013, 62 (5) : 413–419. |
| [12] | Liu H, Xie G, Wang L. Necessary and sufficient conditions for containment control of networked multi-agent systems[J]. Automatica , 2012, 48 (7) : 1415–1422. DOI:10.1016/j.automatica.2012.05.010 |
| [13] | Liu H, Cheng L, Tan M, et al. Containment control of doubleintegrator multi-agent systems with aperiodic sampling: A small-gain theorem based method[C]//Proceedings of the 33rd Chinese Control Conference. Piscataway, NJ, USA: IEEE, 2014: 1407-1412. |
| [14] | Notarstefano G, Egerstedt M, Haque M. Containment in leader-follower networks with switching communication topologies[J]. Automatica , 2011, 47 (5) : 1035–1040. DOI:10.1016/j.automatica.2011.01.077 |
| [15] | Li Z, Ren W, Liu X, et al. Distributed containment control of multi-agent systems with general linear dynamics in the presence of multiple leaders[J]. International Journal of Robust Nonlinear Control , 2013, 23 : 534–547. DOI:10.1002/rnc.v23.5 |
| [16] | Li J, Ren W, Xu S. Distributed containment control with multiple dynamic leaders for double-integrator dynamics using only position measurements[J]. IEEE Transactions on Automatic Control , 2012, 57 (6) : 1553–1559. DOI:10.1109/TAC.2011.2174680 |
| [17] | Rockafellar R T. Convex analysis[M]. Princeton, NJ, USA: Princeton University Press , 1972 . |
| [18] | Liu H, Xie G, Wang L. Necessary and sufficient conditions for containment control of networked multi-agent systems[J]. Automatica , 2012, 48 (7) : 1415–1422. DOI:10.1016/j.automatica.2012.05.010 |
| [19] | Gu K, Kharitonov V L, Chen J. Stability of time-delay systems[M]. Basel, Switzerland: Birkhauser , 2003 . |
| [20] | Jia Y. Robust H∞ Control[M]. Beijing: Science Press , 2007 . |