2. 江苏省大气环境与装备技术协同创新中心, 江苏 南京 210044
2. Collaborative Innovation Center of Atmospheric Environment and Equipment Technology of Jiangsu Province, Nanjing 210044, China
1 引言
自20世纪50年代开始,空间技术得到了迅猛发展,特别是从1957年10月前苏联发射第一颗人造卫星后,人类在航天领域进入了发展的“黄金时代”. 早期的航天器功能相对单一,技术指标要求不高,如早期的自旋稳定航天器的指向精度在1°~10°[1]. 随着科技的进步,太空中的航天器开始承担起各式各样的任务,如军事侦察、 气象预报、 空间探测和导航等. 由于美苏之间的冷战加剧以及人类日益增长的通信需求和对外太空探索的渴望,航天器也经历了从探索到实用、 从结构简单到结构复杂、 从任务单一到任务多样的发展历程.
在现代航天器的发展中,航天器为了完成各种预定的空间飞行任务(如编队飞行、 非合作目标的抓捕和空间碎片的跟踪清理等),均需要进行姿态的机动或者跟踪[2]. 随着航天科技的不断进步,新型材料与新工艺已成功用于航天器制造,以期减轻航天器质量和降低发射成本[3],航天器所携带的设备种类(如太阳能帆板、 侦查相机等)也越发的多样化,同时挠性部件在轨运行期间的转动或展开运动将引起挠性结构变形、 系统参数变化大等问题的产生[4-5]. 另一方面在轨飞行的航天器必将受到各种客观存在的环境力矩(如重力梯度力矩、 气动力矩和太阳辐射压力矩等)的影响. 以上这些问题使得航天器姿态控制系统是一个变参数、 强耦合以及存在各种外干扰的不确定多变量非线性系统. 面对干扰和非线性的存在,部分学者研究发现,H∞方法对挠性航天器这类系统能够产生良好的性能[6-9]. 在文[10-11]中,H∞控制已经被用到姿态控制系统的设计中,其中考虑到了外部扰动与模型的不确定性. 基于线性矩阵不等式(linear matrix inequality, LMI)设计H∞多目标的控制器也在文[12]中提出. 文[13]基于LMI设计了一种改进的抗积分饱和控制器来实现系统的稳定控制. 文[14]设计了基于LMI的抗饱和补偿器,保证了系统在输入受限情况下的闭环稳定. 随着研究的逐渐深入,LMI方法在研究中的作用越来越明显,被广泛应用于航天器的研究中.
另外,由于物理结构和驱动器的能量消耗,输入延迟在挠动航天器中往往是存在的,虽然这不是影响姿态控制的重要因素,但是它会对航天器的性能以及系统的稳定性产生较大的影响[15-16].
因此,将输入时滞考虑到姿态控制设计中是具有实际意义的. 目前,在挠性航天器姿态控制问题研究中对同时含有扰动和输入时滞的研究成果还较少,该问题目前还是具有挑战性的.
受到上述问题的启发,本文主要研究挠性航天器时滞相关H∞控制问题. 通过构造含松弛矩阵的增广李亚普诺夫泛函,建立基于LMI时滞相关状态反馈控制器设计方法. 由于引入了松弛矩阵和时滞积分不等式分解系数,在保证闭环系统的渐近稳定和H∞性能的情况下,该设计更为灵活,保守性更低. 此外,通过数值仿真验证了该控制方法的有效性并分析了时滞量、 H∞性能指标及时滞积分不等式分解系数对闭环系统性能的影响.
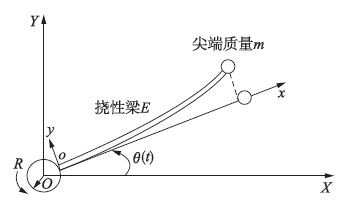
2 问题描述考虑如图 1所示的近似带有挠性附件的航天器模型,它由中心刚体与均匀悬臂梁式挠性附件构成,挠性梁为对称分布,建模时忽略太空重力的影响. 图中OXY和oxy分别为惯性坐标系和本体坐标系,ox与未变形的挠性附件的轴线重合,其原点位于挠性附件与中心刚体的连接处.
|
| 图 1 带挠性附件航天器简化模型 Figure 1 Simplified model of spacecraft with flexible appendages |
利用拉格朗日方法推导挠性航天器的动力学模型为[22]
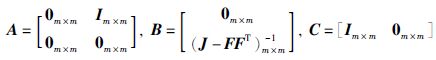
|
(1) |
其中,θ(t)∈R1m×1表示姿态角,J∈Rm×m为卫星的转动惯量矩阵,η(t)∈Rn×1为挠性附件的振动模态,T=diag{2ξ1ω1,…,2ξnωn}∈Rn×n表示模态阻尼矩阵,Λ=diag{ω2,…,ωn2}∈Rn×n表示刚度矩阵,ωi(i=1,…,n)为对应的振动模态的振动频率,ξi(i=1,…,n)为对应的振动模态的阻尼,F∈Rm×n为航天器姿态与挠性结构之间的耦合系数矩阵. u(t-τ(t))∈Rm×1是安装在挠性航天器反作用轮产生的控制力矩,其中τ(t)是时变时滞,且满足如下的条件0≤τ(t)≤τ和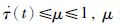
|
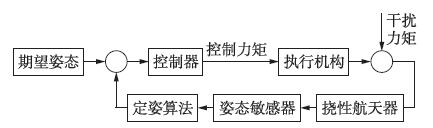
| 图 2 挠性航天器姿态控制 Figure 2 Attitude control for flexible spacecraft |
控制信号从图 2所示的控制器端输入,在执行器执行的过程中会产生时滞现象,即称之为输入时滞. 产生的控制指令作用到执行器上,由于指令传输会产生延时,这种时延一般情况下是不固定的,因此,假设它是时变时滞.
接下来,对系统(1)进一步化简可得:
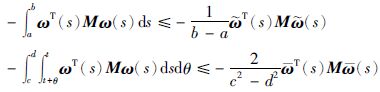
|
(2) |
其中,定义d(t)=F(T(t)+Λη(t))∈Rm×1,即把扰性附件的振动作为对航天器本体的干扰. 同时d(t)属于l2[0,∞),且其欧氏范数满足d(t)≤δd,为描述方便,定义如下向量:
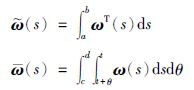
|
(3) |
定义参考输出方程为
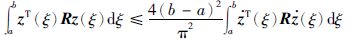
|
(4) |
其中,x(t)∈R2m×1,z(t)∈Rm×1,由此可得系统的状态方程如下:
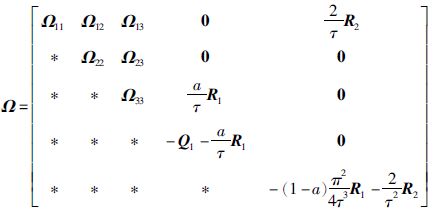
|
(5) |
其中,x(t)是系统的初始值,且
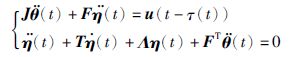
|
对于系统(5),状态反馈控制器可以进行如下设计,即:
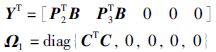
|
(6) |
其中,K∈Rm×2m为需要求解的控制器的增益矩阵,将该状态反馈控制器代入系统(5),可得如下闭环系统:
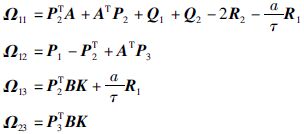
|
(7) |
设计控制器(6)使得闭环系统(7)渐近稳定且满足如下的H∞性能指标
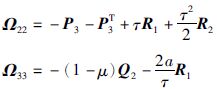
|
(8) |
其中,z(t)2=zT(t)z(t),为此需要如下的引理:
引理 1[18] 对于任何矩阵M>0,标量b>a和c<d<0,则存在一个向量函数ω(s),使得下面的不等式成立:
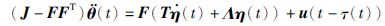
|
其中,
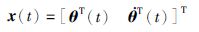
|
引理 2[19] 向量z(t)在[a,b)是一阶可导且导数平方可积并满足z(a)=0. 对于任意的n阶方阵R>0,满足下列不等式:
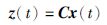
|
定理 1 对于给定的标量γ>0,μ≤1,0<a<1,且时延τ(t)满足0≤τ(t)≤τ,(t)≤μ,如果存在矩阵P1>0,Q1>0,Q2>0,R1>0,R2>0及P2和P3(此处的P1,Q1,Q2,R1,R2,P2,P3均为维数为2m×2m的矩阵)使得下列不等式成立:
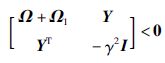
|
(9) |
其中,
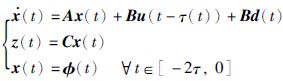
|
“*”表示对称矩阵的对称位置,
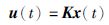
|
且
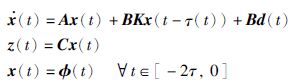
|

|
则闭环系统(7)渐近稳定并在零初始条件下对于任意非零的d(t)∈l2[0,∞),满足z(t)2<γd(t)2.
证明 首先,考虑闭环系统在缺少干扰d(t)时的渐近稳定性. 即系统为
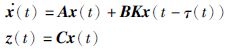
|
(10) |
构造如下的李亚普诺夫泛函:
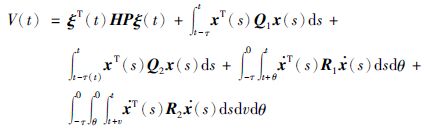
|
其中,
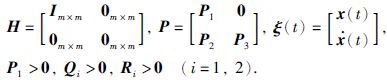
|
然后对V(t)求时间t的导数,得:

|
(11) |
其中,令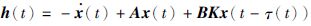
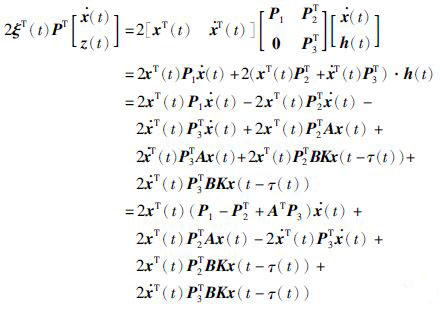
|
(12) |
对于式(11)中,第5项进行分解,得到

|
(13) |
其中,a为时滞积分不等式的分解参数,显然满足0<a<1. 然后,对式(13)中第一部分利用引理1进行放缩,可以得到:
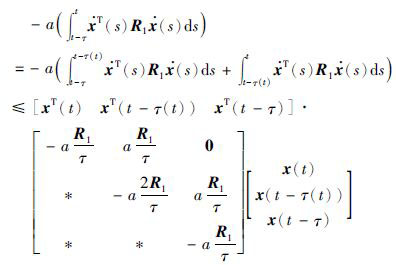
|
(14) |
对式(13)中后一项利用引理2进行放缩,得到如下不等式成立:
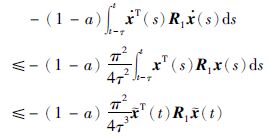
|
(15) |
其中,
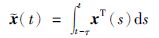
|
对式(11)中第7项,运用引理1进行化简,得
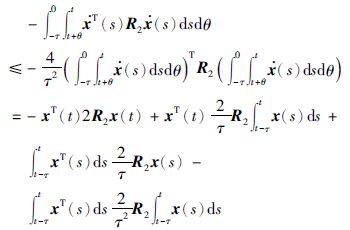
|
(16) |
联合不等式(12)~式(16),于是式(11)进一步化为
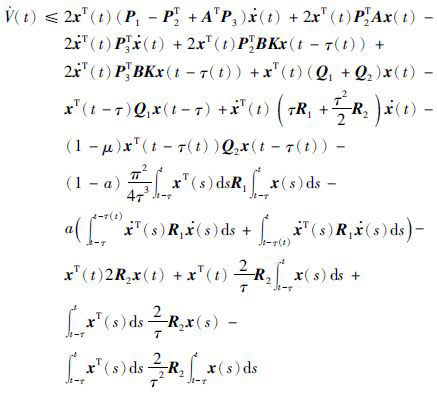
|
(17) |
显然可知:
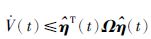
|
其中,Ω如式(9)中所示,且
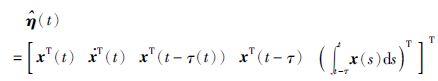
|
因此,闭环系统(10)在是渐近稳定. 接下来进一步考虑初值条件下建立的H∞特性. 令

|
(18) |
可以证明,对于任意非零的d(t)∈l2[0,∞),当t>0,有
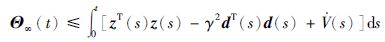
|
(19) |
值得注意的是:
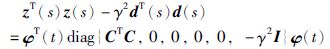
|
(20) |
其中,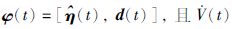
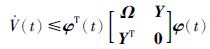
|
(21) |
因此,由式(9)、 式(20)和式(21)可知Θ∞(t)<0,这意味着对于任意非零的d(t)∈l2[0,∞)都有||z(t)||2<γ||d(t)||2,证毕.
注 1 定理1的获得是基于构造了一个含松弛矩阵P2和P3新型增广李亚普诺夫泛函. 对于松弛矩阵的使用,尽管文[20-21]已指出利用等效原理,矩阵P2和P3对降低稳定性判据的保守性是不起作用的. 然而,这样的构造却可以使系统矩阵A、 B与李亚普诺夫函数矩阵P1>0有效进行分离. 这样的分离可以提升控制器增益设计的灵活性.
注 2 与文[22]相比,本文引入了时滞积分不等式分解参数a, 降低文[22]中结果的保守性,比较结果见后续的数值例子部分.
注 3 与文[23]相比,本文引入了时滞环节,对系统考虑的更加周全.
由于定理1还不是一个严格的LMI形式,因此无法求解控制器增益. 于是,基于定理1,可以进一步得到如下定理.
定理 2 给出标量γ>0,μ≤1,ε≠0,0<a<1. 对于任意延迟τ(t)满足0≤τ(t)≤τ,如果存在矩阵P1>0,

|
(22) |
其中,
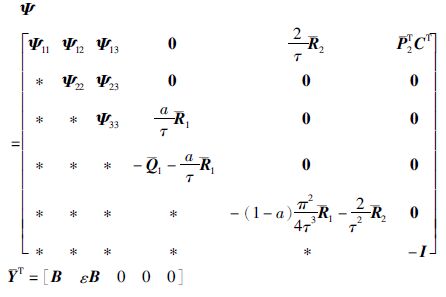
|
且
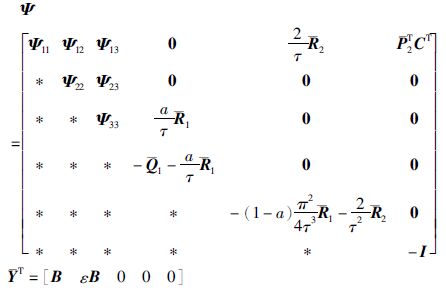
|
那么闭环系统(7)是渐近稳定且在零初始条件下对于任意d(t)∈l2[0,∞)都有||z(t)||2<||γd(t)||2. 此时获得的反馈增益矩阵如下:
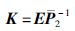
|
(23) |
证明 定义如下矩阵P2=P2-1,P3=εP2,P1=P2TP1P2,Q1=P2TQ1P2,Q2=PT2Q2PT,R1=P2TR1P2,R2=P2TR2P2,将式(22)左乘diag{P2T,P2T,P2T,P2T,P2T,I,I},右乘diag{P2,P2,P2,P2,P2,I,I},得下列不等式:
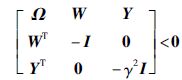
|
(24) |
其中,WT=[C0000]. 对式(21)利用Schur补偿,很显然式(9)是成立的. 因此闭环系统(7)是渐近稳定的并且满足||z(t)||2<γ||d(t)||2,证毕.
4 数值仿真为了验证所提方法的有效性,在Matlab环境下对带挠性附件卫星姿态控制系统进行仿真研究. 以某型航天器为例,考虑其一维动态,卫星俯仰轴的主轴转动惯量为J=35.72 kg·m2,由于低频振动模态占附件振动能量的主要部分,在此忽略高频振动模态的影响,仅考虑挠性帆板的前二阶挠性模态,其振动模态参数为振动频率wi,阻尼比ξi,耦合系数Fi如表 1所示,假定航天器运行高度为500 km的高度轨迹,轨道角速度为0.001 1 rad/s, 假定卫星初始姿态角和角速度分别为θ(0)=0.08 rad, θ·(0)=0.001 rad/s. 令μ=0.1分别通过时滞时间,H∞性能指标、 时滞积分不等式分解参数探究对控制效果的影响.
| 振动模态 | 参数 | |
| 1 | 2 | |
| 振动频率wi/(rad/s) | 3.17 | 7.18 |
| 阻尼比ξi | 0.001 | 0.001 5 |
| 耦合系数Fi/(kg1/2m/s2) | 1.278 14 | 0.917 56 |
当分解参数a为0.1,H∞性能指标γ为0.1,针对不同时滞时间τ,对应的K值如表 2所示.
| 时滞时间/s | 控制增益K |
| τ=0.1 | [-5.235 1 -4.297 4] |
| τ=0.4 | [-2.844 5 -3.426 8] |
| τ=0.8 | [-0.329 2 -2.377 3] |

|
| 图 3 不同τ值时的姿态角响应曲线 Figure 3 Attitude angle response curves for different τ values |
|
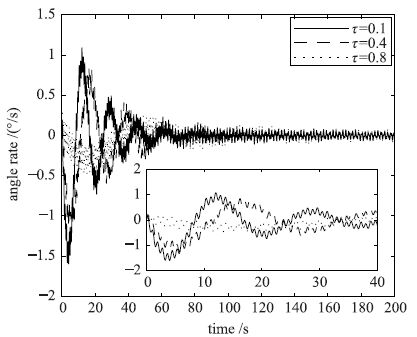
| 图 4 不同τ的姿态角速度响应曲线 Figure 4 Angle rate response curves for different τ values |
由图 3和图 4可知,时滞时间增大会影响姿态角和姿态角速度的响应效果. 图 4中的局部放大图可以更加明显地看出不同τ值下的姿态角速度的效果.
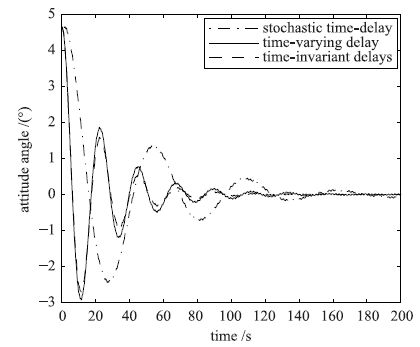
验证系统对不同时滞的影响,仿真结果如图 5所示(分解参数a为0.1,H∞性能指标γ为0.1).
|
| 图 5 不同时滞下的姿态角响应曲线 Figure 5 Attitude angle response curves for different delays |
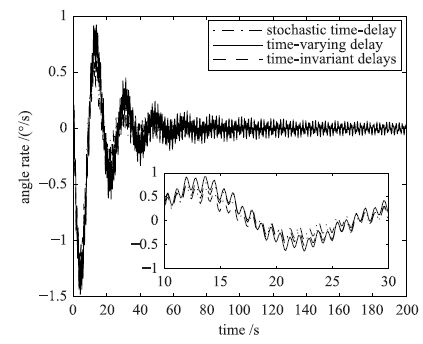
从仿真结果图可以看出对不同的时滞,该系统都能有很好的实验结果. 图 6中局部放大图可以更好地看出在不同时滞类型条件下的姿态角速度的响应曲线.
|
| 图 6 不同时滞下姿态角速度响应曲线 Figure 6 Attitude angle rate response curves for different delays |
当分解参数a为0.1,时滞时间τ为0.4 s, 针对不同的H∞性能指标γ,此时对应的K值如表 3所示.
| H∞性能指标 | 控制增益K |
| γ=0.1 | [-2.844 5 -3.426 8] |
| γ=0.5 | [-4.141 6 -4.799 6] |
| γ=0.9 | [-4.405 2 -4.848 4] |
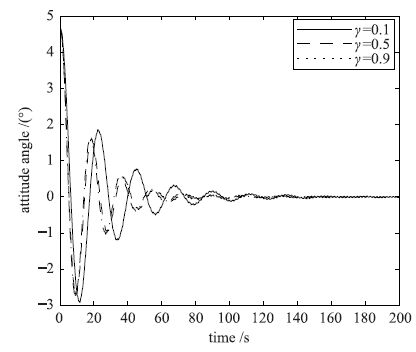
|
| 图 7 不同γ值时的姿态角响应曲线 Figure 7 Attitude angle response curves for different γ values |
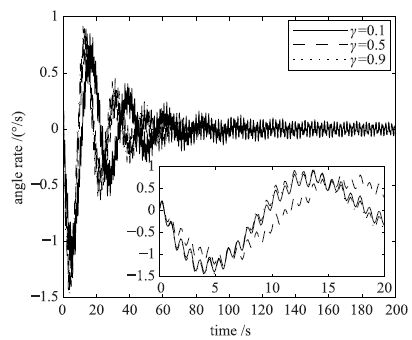
|
| 图 8 不同γ值的姿态角速度响应曲线 Figure 8 Attitude angle rate response curves for different γ values |
由图 7和图 8可知,随着H∞性能指标γ值的逐渐变大,控制器增益K值也变大,响应速度较快. 图 8中局部放大图可以更精确地显示不同γ对应的姿态角速度响应效果.
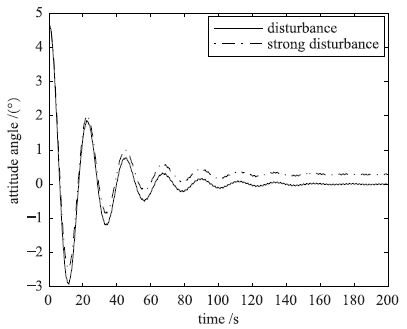
选取分解参数a为0.1,时滞时间τ为0.4 s并且取H∞性能指标γ为0.1. 在仿真中加入强干扰(此处仿真中加入的干扰为4.5e-5(1.5sin(0.001 1t)+cos(0.001 1t)+3)强干扰则取4.5e-3(1.5sin(0.001 1t)+cos(0.001 1t)+3)),通过改变e的不同指数来得到不同的干扰值,然后通过仿真实验,分析该方法的有效性,具体仿真图如图 9所示.
|
| 图 9 不同干扰下的姿态角响应曲线 Figure 9 Attitude angle response curves under different interferences |
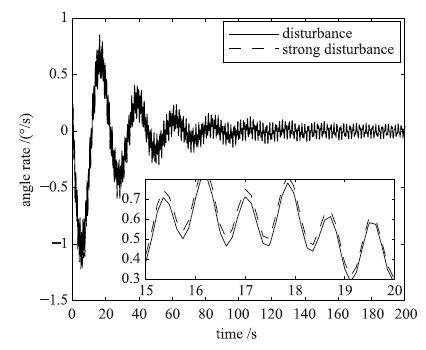
从仿真结果图中可以看出,设计的系统对强干扰也有较好的抑制效果,图 10中的局部放大图更能体现出不同干扰下的抑制效果.
|
| 图 10 不同干扰下的姿态角速度响应曲线 Figure 10 Attitude angle rate response curves under different interferences |
当H∞性能指标γ为0.1,时滞时间τ为0.4 s, 针对不同的分解系数a, 此时对应的K值如表 4所示.
| 分解参数 | 控制增益K |
| a=0.1 | [-2.844 5 -3.426 8] |
| a=0.5 | [-5.974 -12.837] |
| a=0.9 | [-30.985 -40.537] |

|
| 图 11 不同a值时的姿态角响应曲线 Figure 11 Attitude angle response curves for different a values |
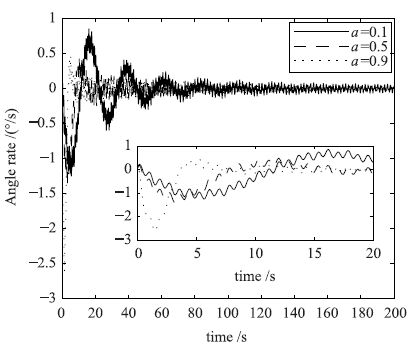
|
| 图 12 不同a值时的姿态角速度响应曲线 Figure 12 Attitude angle rate response curves for different a values |
由图 11和图 12可知,随着分解系数a选取的不同,姿态角和姿态角加速度也会产生大的影响,随着a值的增加,系统的响应速度变快. 图 12中的局部放大图可以更好地看出在不同的分解参数a下的姿态角速度的响应效果.
注 4 在文[22]中由于缺少分解参数a, 因此当H∞性能指标设置为定值时,如: 取γ=0.1,当τ>0.806 s时系统将变得不稳定. 然而,由于构造了分解时滞积分不等式分解参数a, 可以保证取γ=0.1,系统在τ<0.97 s时均能够保证稳定,此时分解参数选为a=0.7,且数值仿真发现随着a值的减小,τ值的最大容许值也在增大,即新加入的时滞积分不等式分解参数a能降低结果的保守性.
5 结论本文建立了基于LMI的挠性航天器状态反馈控制器设计方法,在确保闭环系统渐近稳定的基础上满足给定H∞性能指标. 该方法与其他方法相比,控制器设计更灵活,结果保守性也更低. 此外,从仿真结果可以看出,时滞参数τ和时滞积分不等式分解参数a在取值范围内对闭环系统的影响较为明显.
| [1] | 黄汉文. 自旋稳定静止卫星同步技术分析[J]. 航天器工程 , 1998, 3 (1) : 19–24. Huang H W. The synchronization technology analysis of spin-it stabilized geostationary satellite synchronization[J]. Spacecraft Engineering , 1998, 3 (1) : 19–24. |
| [2] | 刘旺魁. 挠性航天器的姿态机动与跟踪控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. Liu W K. Research on attitude maneuver and tracking for flexible spacecraft[D]. Harbin: Harbin Institute of Technology, 2014. http://cdmd.cnki.com.cn/article/cdmd-10213-1014081888.htm |
| [3] | 郭宁. 可变发射率热控器件的研究进展[J]. 真空与低温 , 2003, 9 (4) : 187–191. Guo N. The development of the variable emittance thermal suite[J]. Vacuum and Cryogenics , 2003, 9 (4) : 187–191. |
| [4] | 黄文虎, 曹登庆, 韩增尧. 航天器动力学与控制的研究进展与展望[J]. 力学进展 , 2012, 42 (4) : 366–394. Huang W H, Cao D Q, Han Z Y. Progress and prospects of spacecraft dynamics and control[J]. Advances in Mechanics , 2012, 42 (4) : 366–394. |
| [5] | Jin E, Sun Z. Passivity-based control for a flexible spacecraft in the presence of disturbances[J]. International Journal of Non-Linear Mechanics , 2010, 45 (4) : 348–356. DOI:10.1016/j.ijnonlinmec.2009.12.008 |
| [6] | Hao X W, Zhou Y R, He H C, et al. Design of output feedback controller for attitude control system of flexible satellite based on LMI[C]//International Conference on Wireless networks and information systems. Piscataway, NJ, USA: IEEE, 2009: 117-120. |
| [7] | Wu B L, Cao X B, Li Z X. Multi-objective output-feedback control for microsatellite attitude control: An LMI approach[J]. Acta Astronautica , 2009, 64 (11/12) : 1021–1031. |
| [8] | Show L L, Juang J C, Jan Y W, et al. Quaternion feedback attitude control design: A nonlinear H-infinity approach[J]. Asian Journal of Control , 2003, 5 (3) : 406–411. |
| [9] | 崔鹏, 张承慧, 张玫. 随机不确定系统谱配置受限的鲁棒H∞无穷控制[C]//2013中国控制与决策会议. 皮斯卡特维, 新泽西州, 美国: IEEE, 2013: 2568-2572. Cui P, Zhang C H, Zhang M. Robust H∞ control for uncertain stochastic system with spectral restraint[C]//2013 Control and Decision Conference (CCDC). Piscataway, NJ, USA: IEEE, 2013: 2568-2572. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-KZJC201309001483.htm |
| [10] | Ballois S L, Duc G. H-infinity control of an earth observation satellite[J]. Journal of Guidance Control and Dynamics , 1996, 19 (3) : 628–635. DOI:10.2514/3.21667 |
| [11] | Byun K W, Bong W, Geller D. Robust H∞ control design for the space station with structured parameter uncertainty[J]. Journal of Guidance Control and Dynamics , 1996, 14 (6) : 1115–1122. |
| [12] | Charbonnel C. H∞ and LMI attitude control design: Towards performances and robustness enhancement[J]. Acta Astronautica , 2004, 54 (5) : 307–314. DOI:10.1016/S0094-5765(03)00049-3 |
| [13] | Boyd S, El Ghaoui L, Feron E. Linear matrix inequalities in system and control theory[M]. Philadelphia, PA, USA: Society for Industrial amd Applied Mathematics , 1994 . |
| [14] | 王明钊, 刘金琨. 基于LMI的挠性航天器抗饱和补偿器设计及分析[J]. 航天控制 , 2014, 12 (1) : 63–67. Wang M Z, Liu J K. The anti-windup compensator design and analysis for the flexible spacecraft based on the LMI method[J]. Aerospace Control , 2014, 12 (1) : 63–67. |
| [15] | Li X F, Guo L, Zhang Y M. A composite disturbance observer and H∞ control scheme for flexible spacecraft with time-varying input delay[C]//31th Chinese Control Conference. Piscataway, NJ, USA: IEEE, 2012: 2824-2829. |
| [16] | Dong C Y, Xu L J, Chen Y, et al. Networked flexible spacecraft attitude maneuver based on adaptive fuzzy sliding mode control[J]. Acta Astronautica , 2009, 65 (11/12) : 1561–1570. |
| [17] | 刘丽娜. 成本控制有效方法的探讨[J]. 山东轻工业学院学报 , 2003, 17 (1) : 56–61. Liu L N. Discussion on the effective method of cost control[J]. Shandong Institute of Light Industry , 2003, 17 (1) : 56–61. |
| [18] | Feng Z G, Lam J. Stability and dissipativity analysis of distributed delay cellular neural networks[J]. IEEE Transactions on Neural Networks , 2011, 22 (6) : 976–981. DOI:10.1109/TNN.2011.2128341 |
| [19] | Liu K, Fridman E. Wirtinger′s inequality and Lyapunov-based sampled-data stabilization[J]. Automatica , 2012, 48 (1) : 102–108. DOI:10.1016/j.automatica.2011.09.029 |
| [20] | Li T, Guo L, Lin C. Stability criteria with less LMI variables for neural networks with time-varying delay[J]. IEEE Transactions on Circuits and Systems II - Express Briefs , 2008, 55 (11) : 1188–1192. DOI:10.1109/TCSII.2008.2004539 |
| [21] | Li T, Ye X L. Improved stability criteria of neural networks with time-varying delays: An augmented LKF approach[J]. Neurocomputing , 2010, 73 (4/5/6) : 1038–1047. |
| [22] | Zhang R, Li T, Guo L. H∞ Control for flexible spacecraft with time-varying input delay[J]. Mathematical Problems in Engineering , 2013 : Article ID 839108. |
| [23] | Liu H, Guo L, Zhang Y M. An anti-disturbance PD control scheme for attitude control and stabilization of flexible spacecrafts[J]. Nonlinear Dynamics , 2012, 67 (3) : 2081–2088. DOI:10.1007/s11071-011-0130-3 |



