2. 三一重工股份有限公司, 湖南 长沙 410100
2. SANY Heavy Industry Cooperation Limited, Changsha 410100, China
1 引言
电液伺服系统具有高效节能、 易于调节等特点,已广泛应用于各类工业控制领域. 但在实际应用中,电液伺服系统存在死区、 泄漏和阻尼等固有特性及外负载突变和交叉耦合等强干扰问题,使得被控对象呈现典型的非线性、 时变性和不确定性[1-3],其动静态特性十分复杂,且难以建立精确的数学模型.
控制策略直接决定系统的控制性能,理想的控制策略要求能同时兼顾系统的快速性、 准确性和稳定性. 对于电液伺服系统,采用常规固定参数PID控制,一般只能处理一些量变和渐变的不确定性情形[4-6],较难获得满意的控制效果,特别是当对象模型参数变化或负载扰动超过一定范围时,系统控制性能下降明显. 因此,诸如具有参数自整定功能的模糊PID控制算法得到了应用[7-8],其控制指标明显优于常规PID控制系统,但模糊PID控制在应用过程中也存在一些问题[9-10],如控制规则不能在线调整,对控制状态变化的自适应性能较弱,不能很好地满足整定参数的控制范围需求; 总结模糊控制规则比较困难,为了保证整定参数的控制精度,需要一定数量较复杂的的模糊控制规则; 模糊化和反模糊化过程缺乏系统的方法,隶属度函数选择及边界确定主要靠经验和试凑; 控制算法运算量大,参数繁多,工业现场调试困难等.
基于电液伺服系统的非线性、 时变性、 不确定性及负载突发强干扰事件等原因,使得被控对象状态由渐变问题转化为难以控制的未预见性、 非渐变或质变的问题[4-6],对于这一类复杂系统,必须引入一个开放性的问题转换环节,可拓控制[6, 11-14]就是一种合适的选择. 可拓控制研究控制矛盾问题的转化方法,适合于处理非渐变的和质变的控制情形,其基本原理是建立控制状态信息的合格度,以信息的合格度作为确定控制策略转变的依据,在不同的论域内采用不同的控制方式,使每一种控制方式在其能进行有效控制的范围内达到理想的控制效果. 本文针对常规PID控制器只能处理渐变控制问题的局限性,结合可拓控制善于处理质变和非渐变控制问题的特点,探讨运用可拓方法对PID控制进行互补,将可拓控制植入PID控制中,建立一种新型的控制策略——可拓自适应PID控制,并应用于电液比例阀位置伺服控制系统,从而实现控制状态有效转换到合格范围内,达到期望的控制目标.
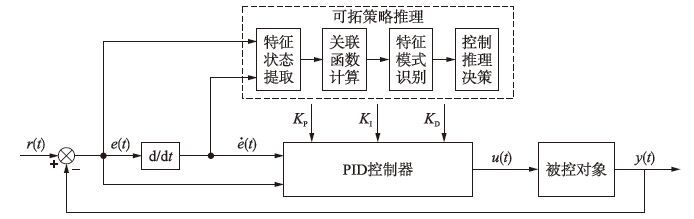
2 可拓自适应PID控制器可拓自适应PID控制是一种基于系统特征状态的控制方法. 图 1所示为控制系统结构图,可拓自适应PID控制器由常规PID控制器和可拓策略推理两部分组成. 可拓策略推理[11-12]的核心思想就是根据被控对象动态过程所提供的特征状态,建立关于特征状态的关联函数,进而划分系统特征模式,进行推理决策,切换控制方式并在线自适应、 自整定PID控制器参数,完成控制状态的有效转变.
|
| 图 1 可拓自适应PID控制系统结构图 Figure 1 The structure of extension adaptive PID control system |
定义1 描述系统状态的特征量集合称为特征状态[10, 15-16]. 一般取误差e和误差变化率为控制系统特征量,特征状态记为S(e, ).
由控制指标决定的系统特征状态的取值范围称经典域,记误差及误差变化率的经典域区间为Eo=(-eom,eom)及
在选定操纵变量条件下,系统可调节的特征状态最大取值范围为节域,记系统可调的最大误差范围和误差变化率范围为Ep=(-em,em)及E
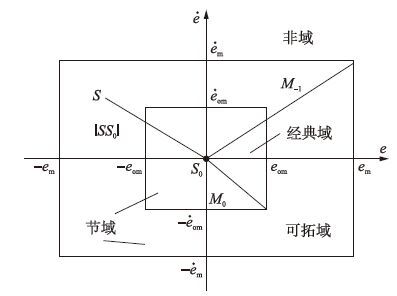
经典域、 节域的划分构成了控制策略转换的可拓论域[17]. 关于e-e特征平面,各可拓论域划分如图 2中所示.
|
| 图 2 特征平面及可拓论域 Figure 2 Characteristic plane and extension domain |
对于图 2特征平面,建立刻划控制状态合格程度的关联函数,并作为解决控制矛盾问题的转化依据.
设特征平面原点S0=(0,0),并记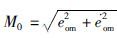
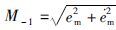
定义2 对于e-e特征平面,系统特征状态S(e, e)满足关联函数[11-12, 14]
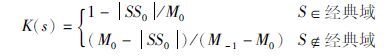
|
(1) |
式中,SS0=e2+2称为状态S和S0的状态距.
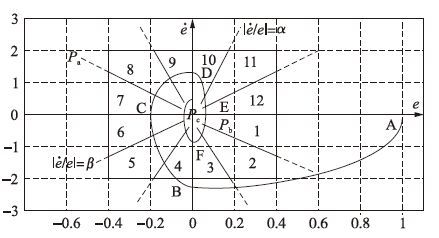
图 3所示为一被控对象典型阶跃响应下的特征状态相平面轨迹[15-16],状态AB段为控制系统起动区,BC段、 DE段为制动区,CD段、 EF段为回调区.
|
| 图 3 相平面轨迹的特征模式划分 Figure 3 Characteristic mode partition of phase plane trajectory |
依据关联函数K(s)取值,可将特征状态相平面轨迹划分为3类基本特征模式:
(1) Pc={Sc0≤K(s)≤1}为经典域,表示特征状态S符合控制指标. K(s)越大,符合系统控制要求的程度越好.
(2) Pb={Sb-1≤K(s) <0}为可拓域,特征状态属于可控渐变的情形,表示在所选控制策略下,可以通过改变控制量的值而使特征状态转变到符合控制要求的范围. K(s)越趋近0,实现上述控制状态转变越可行,K(s)越趋近-1,则特征状态发生质变不可控的可能性越大.
(3) Pa={SaK(s)<-1}处于非域,特征状态属于质变不可控的情形,即在所选控制策略下,无法通过改变控制量的值使特征状态转变到符合控制要求的范围内,此时需要变换控制方式,将特征状态转变到可控范围.
对于特征模式Pb,结合e·e乘积的正负及/e的取值大小,对可拓域作进一步细分. 例如,图 3中区域1~12所示各特征模式:
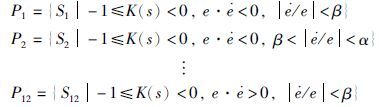
|
可见特征模式Pb=∪Pi,(i=1,2,…,12).
划分特征模式是为了在不同模式内采用最优控制策略或整定控制算法参数,以改进系统的控制效果,实现控制状态有效转换到合格范围.
2.2 PID参数整定依据特征状态的关联函数K(s),设计电液伺服系统可拓自适应PID控制系统的多模态输出控制算法为:
(1) 特征模式Pc: 电液伺服系统满足控制指标,结合对象的大滞后特点,为防止输出频繁调整以稳定系统响应,可采用保持控制模态. 实际运行中,为消除扰动和系统增益的不确定性,获得较高的控制精度,应附加一小范围控制修正量δ,即
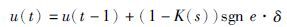
|
(2) |
式中,u(t-1)为前一采样时刻控制器的输出,sgn e为误差e的符号函数,即
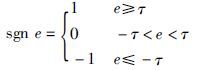
|
(3) |
式中,τ为小正数,一般取为系统的稳态误差.
(2) 特征模式Pa: 对应非域,特征状态无法有效转变到符合控制要求的范围,此时需要改变控制方式. 对于电液伺服系统突加输入、 非线性、 负载强干扰而引起的特征状态质变问题,为将特征状态快速转换到有效控制范围内,并提高系统响应速度,可采取尽可能大的控制作用. 例如对于图 3中AB段起动区,采用bang-bang控制模态,控制器的输出取为
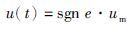
|
(4) |
式中,um为控制器输出最大限幅值,sgn e取值同式(3).
(3) 特征模式Pb: 处于可拓域,采用PID控制算法接近控制目标. 对各细分模式Pi,依据特征状态S整定PID控制参数,确保控制过程自适应电液伺服系统参数时变、 模型不确定的量变和渐变情形,兼顾系统的动静态控制要求.
先定量计算可拓域内各特征量控制合格度[17-18],对于特征状态S(e, e),设关于控制误差的合格度为λ(e),关于误差变化率的合格度为λ(e),则
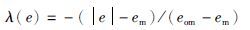
|
(5) |
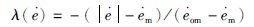
|
(6) |
λ(e)、 λ(e)和K(s)三项变量反映了误差、 误差变化率在e-特征平面上取值大小,可直接作为PID参数整定的依据.
一般地,可归纳出在可拓域内不同特征状态S(e, e)下,被控过程对PID参数KP、 KI及KD的自整定规则[15-16, 19]:
Rule1: 当|e|较大时,为加快系统响应速度,防止积分饱和,避免系统响应出现较大的超调,取较大的KP、 较小的KI值.
Rule2: 当|e|和为中等大小时,为使系统响应超调减少,KI应取较小的值,KP、 KD取值适中,以保证系统的响应速度.
Rule3: 当|e|较小时,为减少系统稳态误差,应增大KI值,同时为避免系统在设定值附近出现振荡,并考虑系统的抗干扰性能,应选取适当的KD值.
Rule4: 误差变化越大时KP取值越小、 KI取值越大,KD取选值适度以避免微分过饱和; 越小时KP取值越大、 KI取值越小,KD取值稍大.
参照图 3可拓域内的相平面轨迹,对回调区CD段、 EF段,特征状态依次进入特征模式7、 8、 9或特征模式1、 2、 3时,控制参数KP递减、 KI递增、 KD递增; 对制动区BC段、 DE段,特征状态依次进入特征模式4、 5、 6或特征模式10、 11、 12时,控制参数KP递增、 KI递减、 KD递减; 每一特征模式下若特征状态越趋近经典域,KP取值越小、 KI取值越大、 KD取值适度增大.
因此对可拓域内各特征模式,设计PID参数与关联函数之间的映射关系为
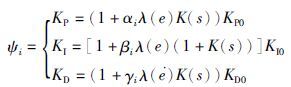
|
(7) |
式中,i=1,2,…,12为特征模式序数; αi、 βi与γi均为小于1的正系数,表示不同特征模式下各PID参数的调整率; KP0、 KI0及KD0是PID参数预设值,可通过仿真或实验确定.
若部分特征模式取相同的参数调整率,则简化推理规则集如表 1所示.
| 序号 | 模式 | 决策 |
| 1 | P1,P6,P7,P12 | ψ1 |
| 2 | P2,P5,P8,P11 | ψ2 |
| 3 | P3,P4,P9,P10 | ψ3 |
PID参数整定推理形式以特征模式集P为条件,策略算法集ψ为结论,即
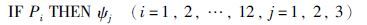
|
(8) |
综上所述,可拓自适应PID控制器输出算法如下:

|
(9) |
式中,T是采样控制周期,t为当前时刻.
可拓自适应PID控制实质上可以看作控制特征状态的转化过程,即使被控量从不可控范围转化到可控范围,使控制指标从不合格到合格的过程. 控制过程中,首先利用关联函数K(s)作为被控信息的转化“路标”,定性划分出特征状态S量变可控与质变不可控、 以及符合与不符合控制要求的界线; 其次针对不同的控制特征状态S,则以定量的方法,确定相应的控制输出,即:
① K(s)≥0时,系统达到满意的控制效果,采用保持控制以稳定被控状态;
② -1≤K(s)<0时,被控量处于可转变的可控范围,依据关联函数及各特征量的合格度,自适应整定PID控制参数,快速准确地将特征状态转化到符合控制要求的经典域.
③ K(s)<-1时,被控量处于不可控范围. 采用bang-bang控制等可拓控制变换手段解决矛盾问题[18],使特征状态转化到可控范围,然后再采用PID控制达到期望的控制效果.
从输入输出角度看,K(s)≥0时可看作有死区的PID,K(s)<-1时可看作PID控制输出饱和限幅,是可拓自适应PID控制器的运行特例.
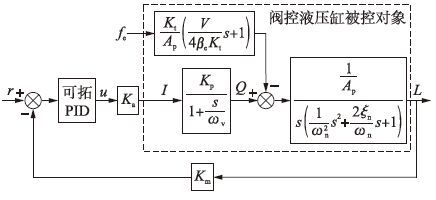
3 电液伺服系统的仿真研究图 4所示为某型泵车臂架电液比例阀位置伺服控制系统[5],各环节分别为可拓PID控制器、 比例放大环节Ka、 位置反馈环节Km及阀控液压缸被控对象.
|
| 图 4 智能臂架电液位置伺服控制系统 Figure 4 Electro-hydraulic position servo system of Intelligent arm frame |
阀控液压缸由电液比例阀、 液压缸及负载组合构成,对其模型近似线性化处理[1-3],得传递函数为

|
(10) |
式中,L为液压缸活塞位移量(m),fe为等效作用在活塞上的外负载(N),I为比例放大环节输出的驱动电流(A).
结合工程实际,阀控液压缸仿真模型中各主要参数标称值如表 2所示.
| 参数符号 | 参数含义 | 标称值 |
| Kq | 比例阀静态流量增益 | 1.2×10-4 |
| Kt(1/s·Pa) | 总流量压力系数 | 2.6×10-10 |
| β/e(Pa) | 有效体积弹性模数 | 7.5×108 |
| ωn(rad/s) | 液压缸固有频率 | 224 |
| ωv(rad/s) | 比例阀固有频率 | 942 |
| Ap(m2) | 活塞有效面积 | 4.1×10-2 |
| V(m3) | 液压缸总容积 | 6.4×10-3 |
| ξn | 液压缸阻尼比 | 0.2 |
文[4-8]指出,阀控液压缸对象有较大的非线性和时变性,表 2中多项参数随着液压缸工作状态、 温度等的变化而变化,个别参数值摄动比较大,幅度可达几十倍; 另外还需考虑外负载fe可能出现的较大扰动.
取比例放大环节Ka=1/12(A/V),位置反馈环节Km=1/1.1(m-1).
针对图 4阀控液压缸对象,在Matlab/Simulink中构建可拓自适应PID控制系统,采用ode45仿真算法,采样周期20 ms. 作为对比,同时设计常规PID控制器及模糊自适应PID控制.
首先基于文[20],采用Ziegler-Nichols整定规则设计常规PID控制器,得KP=3.8、 KI=6.1、 KD=0.4,并将此参数设置为可拓自适应PID及模糊自适应PID两类控制器的参数初始值KP0、 KI0及KD0.
可拓自适应PID控制器其他参数设置为: m=0.1、 eom=0.05、 m=2、 em=0.5、 um=12、 αi=βi=γi=0.3(i=1,2,3).
参考文[7]中模糊自适应PID控制策略,其控制参数增量ΔKP、 ΔKI及ΔKD由带自校正因子μi(i=1,2,3)的模糊控制规则〈μiE+(1-μi)Ec〉在线自适应调整计算. 各参数设置为: e及的基本论域分别为[-0.6,+0.6]、 [-60,+60],模糊论域语言变量值E及Ec均取{NB,NM,NS,ZO,PS,PM,PB}={-3,-2,-1,0,1,2,3},偏差与偏差变化隶属函数曲线取三角型; 自校正因子μi的论域取为[0, 1],语言变量值为{VB,MB,B,S,MS,VS}={1,0.8,0.6,0.4,0.2,0},自校正因子隶属函数取高斯型; 输出语言变量U为{NB,NM,NS,ZO,PS,PM,PB}={-3,-2,-1,0,1,2,3},采用重心法进行反模糊化,并取um=12.
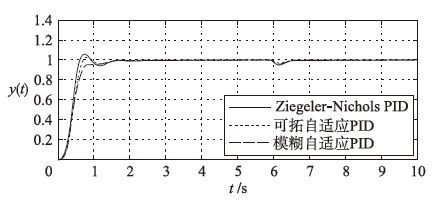
图 5所示为各控制算法的位置跟踪仿真曲线,0 s, <t <6 s期间为阶跃输入下的位置跟踪阶段; t >6 s后为负载fe加载扰动时的位置恢复阶段,位置输出采用标幺值刻度. 仿真结果表明,对比于常规PID控制器及模糊自适应PID控制,可拓PID控制器具有较理想的过渡过程,能实现控制状态的有效转变,其位置跟踪快速平稳,控制精度高、 无振荡、 超调小且调节时间短; 系统对负载扰动变化具有较好的适应能力、 位移量能快速恢复到预设位置,抗干扰鲁棒性好等.
|
| 图 5 位置跟踪曲线 Figure 5 Position tracking curve |
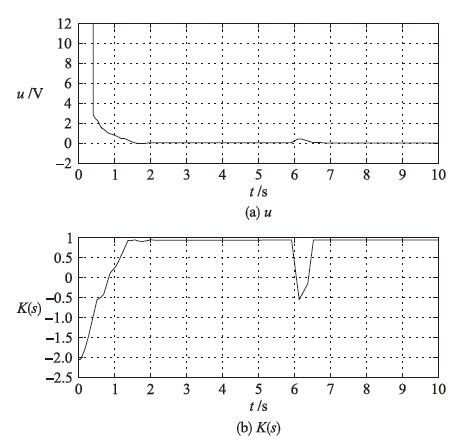
图 6为可拓PID控制输出电压u及关联函数K(s)的变化曲线. 由控制输出电压曲线可知,控制模态过渡比较平滑,设计合理. 当0 s <t<0.5 s时,K(s)<-1,bang-bang控制模式工作,输出最大控制电压12 V,迅速减小偏差; 当0.5 s<t<1.0 s时,-1≤K(s)<0,可拓自适应PID控制器工作,自动调整PID参数并输出合适的控制电压,继续减小偏差接近控制目标; 当t >1.0 s时,K(/s)≥0,控制达到要求,采用保持控制稳定输出电压并在小范围内微调,避免较大的超调和稳态误差. 同理,当t>6 s时,系统再依次启用可拓自适应PID控制和保持控制,消除加载引入的扰动变化,快速恢复到预设位置.
|
| 图 6 控制输出电压及关联函数曲线 Figure 6 The curve of control output and correlation function |
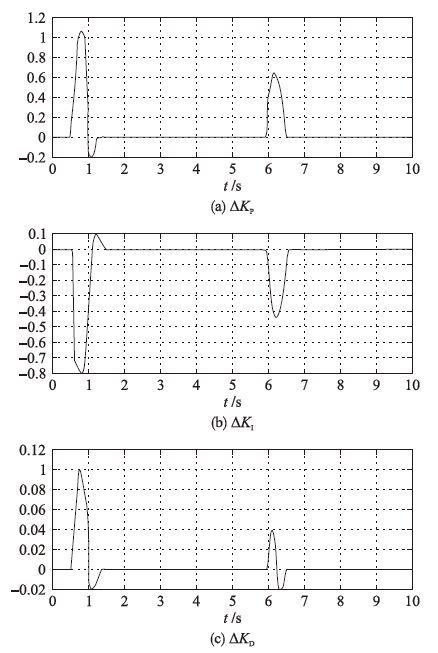
图 7为可拓PID参数修正值ΔKP、 ΔKI及ΔKD的实时同步调整曲线. 在bang-bang控制及保持控制阶段,PID参数默认为预设值,参数修正量为0.
|
| 图 7 PID参数修正值的调整曲线 Figure 7 The adjust curve of PID parameter correction value |
0.5 s <t<1.0 s及t >6 s加载扰动后,系统处于可拓PID控制阶段,基于式(7)自适应整定算法,可得PID参数修正值分别为ΔKP=αiλ(e)K(s)KP0、 βiλ(e)(1+K(s))KI0及ΔKD=γiλ(e)K(s)KD0. 对比图 3及图 5曲线可知,系统特征状态S以类似于图 3的ABCD轨迹依次进入制动区和回调区等,特征量e及在可拓域内逐步减小. 控制过程中关联函数K(s)在(-1,0)区间变化,与此同时,特征量合格度λ(e)、 λ(e)将出现从-1到小正数的过渡,将其代入PID参数修正计算式分析,与图 7各调整曲线吻合,表明可拓控制方法能自适应调节PID参数满足整定要求,以适应被控对象的状态转换. 例如分析阶跃输入下位置跟踪阶段的制动区及回调区,当误差e较大时,修正值ΔKP取正加大比例作用,ΔKI为负减弱积分作用,以加快动态过程并预防积分饱和; 当误差e逐步较小时,ΔKP为负减弱比例作用,ΔKI取正加大积分作用,以避免较大的超调并减少系统稳态误差; 控制过程中误差变化逐步较小,ΔKD取值由正到负且变化幅度适中,以保证系统动态响应速度及稳态时的抗干扰能力.
4 结论本文结合可拓理论,提出了可拓自适应PID控制策略,并应用于电液伺服位置控制系统. 对比常规PID或模糊PID控制方式,可拓自适应PID控制策略具有以下的特点:
(1) 从控制问题上看,控制策略能很好地模拟人类运用变通性和创造性处理控制矛盾问题的过程,善于运用变换或替代的不同控制机制处理被控过程中质变的、 突发的或未预见性的状况.
(2) 从控制方法上看,控制策略是一种定性和定量相结合的分析方法,它依据系统特征状态的合格度而切换控制方式和整定PID参数,既能定性把握控制过程中被控对象及其特征的质变,也能用定量计算来补充说明事物质变中量与度的概念,为处理控制矛盾问题转化提供有力的工具.
(3) 从控制对象上看,控制策略不依赖于控制系统的结构信息,不需要预知对象的数学模型,因此能较好地应用于非线性、 时变或不确定的复杂控制领域.
初步研究表明,基于可拓自适应PID控制的电液伺服系统具有良好的控制品质,系统响应速度快、 控制精度高、 抗负载干扰能力强,能实现控制状态的有效转变和平滑切换. 控制策略满足系统要求,且参数整定简单、 工程实现方便,是自适应PID控制的一种有益补充. 目前,可拓自适应PID控制策略还有一些需要深入研究的问题,比如直接决定控制效果的关联函数的建立方法、 PID控制参数最优整定规则等. 总之,建立并完善可拓自适应PID控制策略具有理论意义和实用价值.
| [1] | 刘军龙, 姜继海, 欧进萍, 等. 直驱容积控制电液伺服系统模型与动态特性[J]. 哈尔滨工业大学学报 , 2011, 43 (7) : 61–65. Liu J L, Jiang J H, Ou J P, et al. Theoretical model and dynamic performance of direct drive volumecontrol electro-hydraulic servo system[J]. Journal of Harbin Institute of Technology , 2011, 43 (7) : 61–65. |
| [2] | 高强, 金勇, 王力, 等. 泵控缸电液位置伺服系统建模研究[J]. 兵工学报 , 2011, 32 (8) : 950–956. Gao Q, Jin Y, Wang L, et al. Modeling of electro-hydraulic position servo systems of pump-controlled cylinder[J]. Acta Armamentarii , 2011, 32 (8) : 950–956. |
| [3] | 柏艳红, 权龙, 郝小星, 等. 基于流量近似的阀控液压缸动力机构建模[J]. 机械工程学报 , 2014, 50 (24) : 179–185. DOI:10.3901/JME.2014.24.179 Bai Y H, Quan L, Hao X X, et al. Modeling of hydraulic valve-controlled cylinder power mechanism based on flow approximation[J]. Journal of Mechanical Engineering , 2014, 50 (24) : 179–185. DOI:10.3901/JME.2014.24.179 |
| [4] | 王幼民, 范恒灵. 基于正交试验法的电液伺服系统PID控制[J]. 农业机械学报 , 2007, 38 (7) : 196–198. Wang Y M, Fang H L. PID controller of electro-hydraulic servo system based on orthogonal experiment[J]. Transactions of the Chinese Society for Agricultural Machinery , 2007, 38 (7) : 196–198. |
| [5] | 赵若楠. 混凝土泵车臂架电液系统的PID控制[D]. 北京: 燕山大学, 2012. Zhao R N. PID control of the truck-mounted concrete pump boom electro-hydraulic system[D]. Beijing: Yanshan University, 2012. http://cdmd.cnki.com.cn/article/cdmd-10216-1012025518.htm |
| [6] | Zheng H B, Sun Y S, Li M. Extension control research of pump-control electro-hydraulic servo system[J]. Applied Mechanics and Materials , 2011, 80 (1) : 917–921. |
| [7] | 邵俊鹏, 王仲文, 李建英, 等. 电液位置伺服系统的规则自校正模糊PID控制器[J]. 中南大学学报: 自然科学版 , 2010, 41 (3) : 960–965. Shao J P, Wang Z W, Li J Y, et al. Rule self-tuning fuzzy-PID controller of electro-hydraulic position servo system[J]. Journal of Central South University: Science and Technology , 2010, 41 (3) : 960–965. |
| [8] | Wang Y Q. Direct drive electro-hydraulic servo control system design with self-tuning fuzzy PID controller[J]. Telkomnika-Indonesian Journal of Electrical Engineering , 2013, 11 (6) : 3374–3382. |
| [9] | 黄卫华. 模糊控制系统及应用[M]. 北京: 电子工业出版社 ,2012 : 8 -47. Huang W H. Fuzzy control system and its application[M]. Beijing: Publishing House of Electronics Industry , 2012 : 8 -47. |
| [10] | 胡包钢, 应浩. 模糊PID控制技术研究发展回顾及其面临的若干重要问题[J]. 自动化学报 , 2010, 27 (4) : 567–584. Hu B G, Yin H. Review of fuzzy PID control techniques and some important issues[J]. Zidonghua Xuebao , 2010, 27 (4) : 567–584. |
| [11] | 姜万录, 孙慢. 电液伺服系统的可拓控制策略研究[J]. 机床与液压 , 2005 (1) : 94–97. Jiang W H, Sun M. Study on Extension control tactics of electro-hydraulic servo system[J]. Machine Tool & Hydraulics , 2005 (1) : 94–97. |
| [12] | 王明东, 刘宪林, 于继来. 同步发电机可拓励磁控制器[J]. 电机与控制学报 , 2008, 12 (1) : 1–4. Wang M D, Liu X L, Yu J L. Extension excitation controller of synchronous generator[J]. Electric Machines and Control , 2008, 12 (1) : 1–4. |
| [13] | 刘海兰, 李小平, 芮延年, 等. 模拟月球车复杂路面的可拓自适应控制方法[J]. 机械设计与研究 , 2011, 27 (5) : 76–79. Liu H L, Li X P, Rui Y N, et al. Research on an extendable self-adaptive control used to simulating lunar rover driven on the complex road[J]. Machine Design and Research , 2011, 27 (5) : 76–79. |
| [14] | Lu X Q, Wu C N, Xia X W. Extension control and its application research in power system[J]. Communications in Computer and Information Science , 2012 (345) : 301–306. |
| [15] | Luo Z, Liu H Y, Wang F. Overview of human-simulated intelligent control method and its application[J]. International Journal of Modelling, Identification and Control , 2010, 9 (1) : 161–167. |
| [16] | Dong X M, Li Z S, Yu M. Human simulated intelligent control and its application in magneto-rheological suspension[J]. Control Theory and Applications , 2010, 27 (2) : 249–256. |
| [17] | Yang C Y, Cai W. Extenics: Theory, method and application[M]. Beijing: Science Press , 2013 : 12 -95. |
| [18] | 杨春燕, 蔡文. 可拓工程[M]. 北京: 科学出版社 ,2010 : 183 -201. Yang C Y, Cai W. Extension engineering[M]. Beijing: Science Press , 2010 : 183 -201. |
| [19] | 刘瑞琪. 智能PID参数整定方法的研究[D]. 长沙: 中南大学, 2009. Liu R Q. The researeh for the intelligent PID tuning method[D]. Changsha: Central South University, 2009. |
| [20] | 刘金琨. 先进PID控制MATLAB仿真[M]. 3版. 北京: 电子工业出版社 ,2011 : 84 -95. Liu J K. Advanced PID control MATLAB simulation[M]. Beijing: Publishing House of Electronics Industry , 2011 : 84 -95. |



