1 引言
位置伺服控制系统已经广泛应用于导弹反射架控制、 火炮方位的自动跟踪、 雷达天线控制等[1-2]. 近年来,随着控制理论的不断发展及机械加工精度的日益提高,人们对伺服系统的控制性能有了更高的要求,但传统PID控制在外界扰动过大或电机内部参数发生变化时,往往难以满足精确定位的要求. 如何保证系统具有良好的动静态性能及对参数变化和外界干扰的不敏感性,一直是控制界研究的热点. 文[3]将模糊控制原理与PID结合,设计出模糊自适应的PID,并将其应用于无刷直流电机中. 文[4]将位置伺服系统的滑模控制器设计为位置和速度两段滑模,虽然控制性能得到改善,但参数整定困难. 近年来随着分数阶微积分理论研究的不断深入,将其与控制理论相结合,研究分数阶控制器的设计方法已经引起了控制界的普遍关注[5-7]. 文[8]将传统整数阶滑模切换函数推广到分数阶,设计出全控制域滑模面,并结合模糊控制理论设计了模糊分数阶滑模控制,提高了伺服系统的控制性能,但其实现较为复杂. 文[9]提出了一种关于偏差的分数阶函数,并将其代替偏差作为分数阶PID控制器的输入,结合神经网络理论设计了鲁棒分数阶PI控制器,有效提高了伺服系统的控制性能,但控制器参数较多,增加了整定难度.
考虑到1自由度控制器难以同时兼顾系统的跟随特性和抗扰特性,2自由度(two-degree-of-freedom, 2DOF)控制结构应运而生[10-14]. 2DOF控制可使系统的跟随性能和抗扰性能分别由两个控制器进行调节,较好地满足了高性能控制的要求. 文[15]针对永磁同步伺服电机,设计了一种2DOF控制,但是控制器中5个参数的调整较为复杂. 文[16]针对异步电动机,设计了基于Youla参数化的2DOF控制结构,其中反馈控制器采用H∞混合灵敏度设计,前馈控制器采用H2进行优化,获得了良好的鲁棒性,但设计的2自由度控制器阶次较高,不便于实际应用.
为进一步提高系统的控制性能,本文设计了一种2DOF控制结构,并将分数阶理论和内模控制(internal model control, IMC)相结合,给出了跟随控制器和抗扰控制器的设计方法; 同时利用截止频率和最大灵敏度指标,实现了2DOF控制器参数整定.
2 直流伺服系统的数学模型为简化分析,忽略伺服系统中存在的电机参数、 外部负载的时变性,非线性摩擦及模型中不可预测的不确定项,得直流伺服电机数学模型为
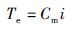
|
(1) |
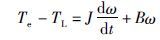
|
(2) |
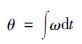
|
(3) |
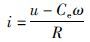
|
(4) |
式中,u为电机输入电压,Ce为电动势系数,R为电枢电阻,i为电枢电流,Cm为转矩常数,Te为电磁转矩,TL为负载转矩,J为转动惯量,ω为转子机械角速度,θ为转子机械位置,B系统粘滞摩擦系数.
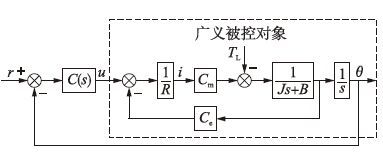
根据式(1)~(4)得到的直流伺服系统简化原理框图如图 1所示,其中C(s)为控制器,r为参考输入.
|
| 图 1 直流伺服系统结构图 Figure 1 Block diagram of the DC servo system |
当电机空载时,伺服系统的数学模型M(s)为
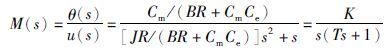
|
(5) |
式中,K=Cm/(BR+CmCe)为系统增益,T=JR/(BR+CmCe)为系统时间常数.
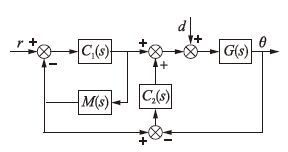
3 2自由度控制结构设计为了同时改善系统的动态响应性能和鲁棒性,本文提出一种2DOF控制结构,如图 2所示. C1(s)和C2(s)分别为2自由度控制器,d为系统输入干扰,它可等效系统的负载转矩干扰.
|
| 图 2 2自由度控制结构 Figure 2 Block diagram of the 2DOF control |
由控制结构图 2可知,C1(s)主要令M(s)获得理想的控制输出,C2(s)负责克服干扰的影响,使G(s)快速跟随M(s)的输出.
|
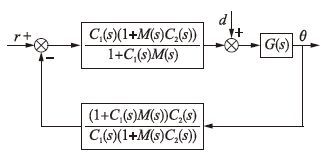
| 图 3 等效2自由度控制系统结构 Figure 3 Block diagram of the equivalent 2DOF control |
由图 3可得系统的开环传递函数L(s)和输出分别为
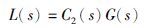
|
(6) |
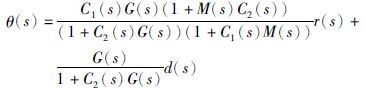
|
(7) |
当模型精确时,即M(s)=G(s),式(7)可改写为
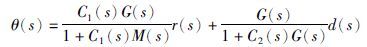
|
(8) |
由式(6)、 (7)和式(8)可得该2DOF结构的特点:
(1) 系统的开环传递函数为L(s)=C2(s)G(s),与C1(s)无关.
(2) 当模型完全匹配时,系统响应的跟随特性仅由C1(s)控制,而抗扰特性仅由C2(s)控制.
(3) 当C1(s)=C2(s)时,2自由度控制系统就相当于简单的闭环控制系统.
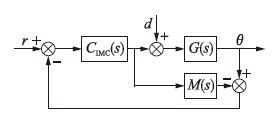
4 控制器设计分数阶内模PID控制器[17-18]不但设计简单,参数整定方便,而且可使系统获得良好的抗干扰特性和鲁棒性,因此可根据内模控制原理设计C1(s)和C2(s). 内模控制结构如图 4所示,其中CIMC(s)为内模控制器.
由内模控制原理可得内模控制器CIMC(s)为
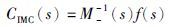
|
(9) |
式中,M-(s)为模型M(s)中稳定的最小相位部分,f(s)为低通滤波器.
|
| 图 4 内模控制结构 Figure 4 Structure of IMC |
内模控制可等效变换为反馈控制结构,反馈控制器C(s)与内模控制器CIMC(s)的关系为
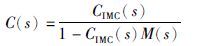
|
(10) |
根据式(5)所示伺服系统数学模型,选择分数阶滤波器:
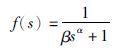
|
(11) |
式中,α为滤波器的分数阶阶次,1≤α <2; β为分数阶滤波器时间常数.
由式(5)和式(9)~(11)得
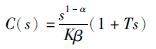
|
(12) |
由式(12)可见,所设计的分数阶控制器中包含2个可调参数,即分数阶滤波器的阶次α和时间常数β. 当α=1时,控制器为整数阶PD控制器; 当1 <α<2时,控制器为分数阶ID控制器.
5 控制器参数整定 5.1 C1(s)控制器参数的整定由控制结构图 2可知,C1(s)主要控制模型为M(s),令其达到满意的控制效果,因而可以将C1(s)和M(s)看作为简单的反馈控制结构,根据式(5)和式(12)可得其开环传递函数L1(s)为
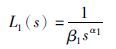
|
(13) |
式中,β1、 α1分别为C1(s)设计过程中分数阶滤波器的时间常数和阶次. 在1≤α1 <2的范围内,α1的取值越大,表明系统开环特性中的积分作用越强,系统的响应的速度越慢,超调越大,跟随性能变差,不符合C1(s)整定的目标,因此α1应取最小值,即:
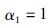
|
(14) |
根据截止频率的定义可得
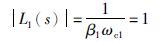
|
(15) |
式中,ωc1为L1(s)回路的截止频率,则:

|
(16) |
β1可根据截止频率ωc1进行整定. 此时,C1(s)为PD控制器,是分数阶控制器的特例.
5.2 C2(s)控制器参数的整定最大灵敏度作为闭环系统的一种鲁棒性能指标[19],能够同时满足增益和相位裕度要求,因此可以用来整定控制器C2(s)的参数.
灵敏度函数定义为
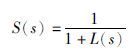
|
(17) |
则最大灵敏度Ms为
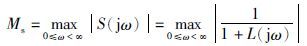
|
(18) |
由C2(s)G(s)可得开环传递函数L2(s)为
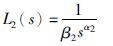
|
(19) |
式中,β2、 α2为C2(s)设计过程中分数阶滤波器的时间常数和阶次,则灵敏度函数为
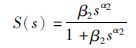
|
(20) |
为了克服系统干扰的影响,保证系统的稳态精度,C2(s)中应包含有积分作用,同时为了发挥分数阶控制的强鲁棒性,此处不考虑α2=1的情况,当1 <α2<2时,灵敏度的幅值为

|
(21) |
对式(21)求极值,当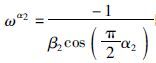
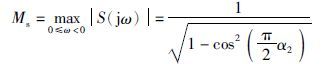
|
(22) |
一般情况下,Ms的取值范围为[1.2,2.0]; Ms取值越小,系统鲁棒性越好.
同样根据截止频率的定义,由式(19)得
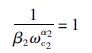
|
(23) |
式中,ωc2为L2(s)回路的截止频率.
由式(22)和式(23)得控制器C2(s)的参数为
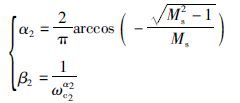
|
(24) |
为验证本文方法的有效性,利用Matlab和QStudioRP实验平台,分别进行了仿真和实验分析.
Quanser公司的MicroMo Coreless无芯电机的主要参数为: 电枢电阻R=2.6 Ω,电动势系数Ce=0.007 67 V·s/rad, 转矩常数Cm=0.007 67 N·m/A,转动惯量J=3.87×10-7 kg·m2,粘滞摩擦系数B=1.5×10-3 N·m·s/rad, 负载等效转动惯量Jeq=9.31×10-5 kg·m2,电机效律ηm=0.69,得系统模型为
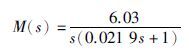
|
(25) |
设计控制器C1(s)、 C2(s)为
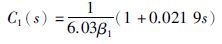
|
(26) |
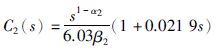
|
(27) |
为保证系统具有良好的跟随特性,根据式(16),选择ωc1=52.3 Hz, 得β1=0.003,为保证系统的抗扰性,根据式(24),选择Ms=1.2,ωc2=23.9 Hz, 得β2=0.001,α2=1.37.
根据文[20]方法设计伺服系统分数阶控制器C(s):
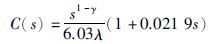
|
(28) |
综合考虑的跟随特性和抗扰性,系统选择截止频率ωc=15.9 Hz, 相角裕度φm=60°进行参数整定,得λ=0.002 2,γ=1.333.
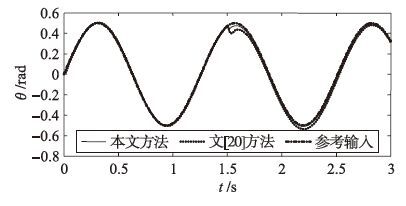
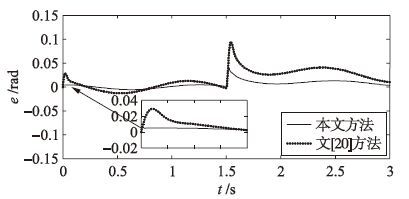
设系统的参考输入r=0.5sin(5t) rad, 输入扰动d=-2(t-1.5) V. 系统的跟踪响应和偏差e变化曲线分别如图 5和图 6所示,本文方法和文[20]方法的跟踪偏差均方根分别为0.007 1 rad和0.020 6 rad, 突加干扰后的最大偏差分别为0.039 58 rad和0.094 93 rad, 系统稳态输出滞后参考输入分别为0.009 95 rad和0.022 7 rad, 可见本文方法的稳态性能、 抗扰性能及动态性能均优于文[20]的方法.
|
| 图 5 标称系统跟踪响应 Figure 5 Tracking response of the nominal system |
|
| 图 6 标称系统的偏差变化曲线 Figure 6 Deviation change curves of the nominal system |
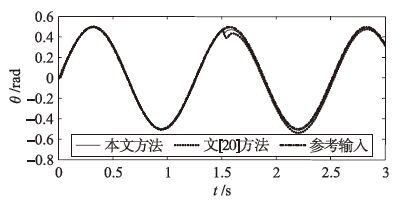
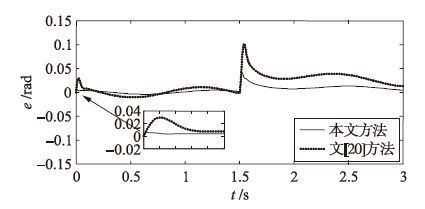
为验证本文方法的鲁棒性,设参数T和K分别摄动+30%和+20%,即T=0.028 47,K=7.236,则系统的跟踪响应和偏差e变化曲线如图 7和图 8所示,本文方法和文[20]方法的跟踪偏差均方根分别为0.006 9 rad和0.02 rad, 突加干扰后的最大偏差分别为0.041 45 rad和0.100 8 rad, 系统稳态输出滞后参考输入分别为0.008 6 rad和0.018 6 rad, 可见本文方法具有良好的鲁棒性.
|
| 图 7 摄动系统的跟踪响应 Figure 7 Tracking response of the perturbed system |
|
| 图 8 摄动系统的偏差变化曲线 Figure 8 Deviation change curves of the perturbed system |
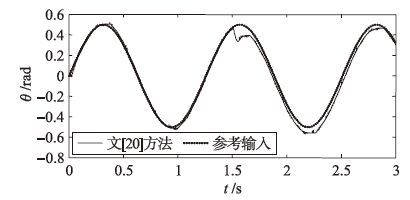
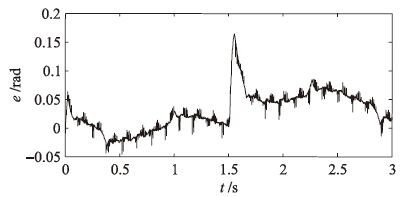
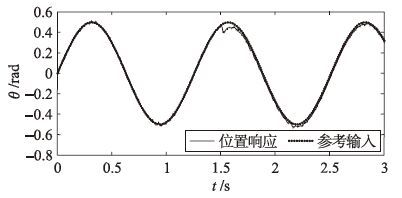
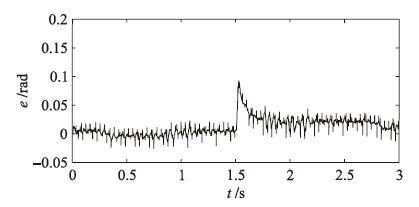
将本文方法应用于基于QstudioRP实验平台的直流伺服系统,系统参考输入r=0.5sin(5t) rad. 当t=1.5 s时,突加-2 V的输入干扰,采样周期为0.001 s. 本文方法、 文[20]方法的跟踪响应和偏差e变化曲线如图 9~12所示,对应的跟踪偏差均方根分别为0.013 5 rad和0.034 9 rad, 突加干扰后的最大偏差分别为0.092 14 rad和0.163 5 rad, 系统稳态输出滞后参考输入分别为0.013 8 rad和0.036 2 rad, 可见本文方法具有更好的控制性能.
|
| 图 9 2自由度控制跟踪响应 Figure 9 Tracking response of the 2DOF control |
|
| 图 10 2自由度的偏差变化曲线 Figure 10 Deviation change curves of the 2DOF control |
针对直流伺服系统提出一种2DOF控制结构,并利用内模控制原理和分数阶理论进行控制器设计,实现了系统位置跟随特性和抗扰特性的解耦控制,其中控制器的参数由最大灵敏度和截止频率解析整定. 将本文方法应用于位置伺服系统中,当跟随0.5sin(5t) rad参考信号时,相比文[20]方法,系统跟踪偏差的均方根减小了61.3%; 突加相同干扰,最大偏差减小了43.6%; 稳态输出滞后角度减小61.8%. 表明了所提方法的有效性和优越性. 如何将文中二自由度控制方法推广应用于实际生产中是下一步的研究方向.
| [1] | Thum C K, Du C, Chen B M, et al. A unified control scheme for track seeking and following of a hard disk drive servo system[J]. IEEE Transactions on Control Systems Technology , 2010, 18 (2) : 294–306. DOI:10.1109/TCST.2009.2017513 |
| [2] | 赵志刚, 林辉, 董国创. 小型雷达伺服系统控制器的设计与研究[J]. 微特电机 , 2013, 41 (5) : 59–61. Zhao Z G, Lin H, Dong G C. The design and research of the small radar servo system controller[J]. Small & Special Electrical Machines , 2013, 41 (5) : 59–61. |
| [3] | Kandiban R, Arulmozhiyal R. Speed control of BLDC motor using adaptive fuzzy PID controller[J]. Procedia Engineering , 2012, 38 : 306–313. DOI:10.1016/j.proeng.2012.06.039 |
| [4] | 胡强晖, 胡勤丰. 全局滑模控制在永磁同步电机位置伺服中的应用[J]. 中国电机工程学报 , 2011, 31 (18) : 61–66. Hu Q H, Hu Q F. Global sliding mode control for permanent magnet synchronous motor servo system[J]. Proceedings of the CSEE , 2011, 31 (18) : 61–66. |
| [5] | Wang D J, Gao X L. H∞ design with fractional-order PDμ controllers[J]. Automatica , 2012, 48 (5) : 974–977. DOI:10.1016/j.automatica.2012.02.012 |
| [6] | Alagoz B B, Ates A, Yeroglu C. Auto-tuning of PID controller according to fractional-order reference model approximation for DC rotor control[J]. Mechatronics , 2013, 23 (7) : 789–797. DOI:10.1016/j.mechatronics.2013.05.001 |
| [7] | Liu L, Pan F, Xue D Y. Variable-order fuzzy fractional PID controller[J]. ISA Transactions , 2015, 55 (3) : 227–233. |
| [8] | 张碧陶, 皮佑国. 永磁同步电机伺服系统模糊分数阶滑模控制[J]. 控制与决策 , 2012, 27 (12) : 1776–1779. Zhang B T, Pi Y G. Fractional order fuzzy sliding mode control for permanent magnet synchronous motor servo drive[J]. Control and Decision , 2012, 27 (12) : 1776–1779. |
| [9] | Zhang B T, Pi Y G. Enhanced robust fractional order proportional-plus-integral controller based on neural network for velocity control of permanent magnet synchronous motor[J]. ISA Transactions , 2013, 52 (4) : 510–516. DOI:10.1016/j.isatra.2013.02.003 |
| [10] | 王维杰, 李东海, 高琪瑞, 等. 一种二自由度PID控制器参数整定方法[J]. 清华大学学报: 自然科学版 , 2008, 48 (11) : 1962–1966. Wang W J, Li D H, Gao Q R, et al. Two-degrees-of-freedom PID controller tuning method[J]. Journal of Tsinghua University: Science & Technology , 2008, 48 (11) : 1962–1966. |
| [11] | Sánchez J, Visioli A, Dormido S. A two-degree-of-freedom PI controller based on events[J]. Journal of Process Control , 2011, 21 (4) : 639–651. DOI:10.1016/j.jprocont.2010.12.001 |
| [12] | Debbarma S, Saikia L C, Sinha N. Automatic generation control using two degree of freedom fractional order PID controller[J]. International Journal of Electrical Power & Energy Systems , 2014, 58 (6) : 120–129. |
| [13] | Xie Y, Alleyne A. A robust two degree-of-freedom controller for systems with both model and measurement uncertainty[J]. Control Engineering Practice , 2014, 25 (4) : 55–65. |
| [14] | Precup R E, Preitl S, Petriu E M, et al. Generic two-degree-of-freedom linear and fuzzy controllers for integral processes[J]. Journal of the Franklin Institute , 2009, 346 (10) : 980–1003. DOI:10.1016/j.jfranklin.2009.03.006 |
| [15] | 李明, 程启明, 陈根, 等. 永磁同步伺服电机二自由度控制[J]. 电机与控制应用 , 2014, 41 (10) : 1673–6540. Li M, Cheng Q M, Cheng G, et al. Two degree-of-freedom control of permanent magnet synchronous servo motor[J]. Electric Machines & Control Application , 2014, 41 (10) : 1673–6540. |
| [16] | 游江, 孟繁荣, 罗耀华. 异步电动机间接磁场定向的二自由度鲁棒控制器[J]. 电工技术学报 , 2009, 24 (5) : 19–23. You J, Meng F R, Luo Y H. Two-degree-of-freedom robust controller of induction motor with indirect field oriented[J]. Transactions of China Electrotechnical Society , 2009, 24 (5) : 19–23. |
| [17] | Jin Q, Liu Q. IMC-PID design based on model matching approach and closed-loop shaping[J]. ISA Transactions , 2014, 53 (2) : 462–473. DOI:10.1016/j.isatra.2013.11.005 |
| [18] | Bettayeb M, Mansouri R. Fractional IMC-PID-filter controllers design for non integer order systems[J]. Journal of Process Control , 2014, 24 : 261–271. |
| [19] | 周铁军, 王昕, 王振雷. 基于最大灵敏度指标的分数阶PID参数最优整定方法[J]. 控制工程 , 2014, 21 (6) : 1001–1005. Zhou T J, Wang X, Wang Z L. Optimal turning method of fractional PID controller based on sensitivity index[J]. Control Engineering of China , 2014, 21 (6) : 1001–1005. |
| [20] | Maâmar B, Rachid M. IMC-PID-fractional-order-filter controllers design for integer order systems[J]. ISA Transactions , 2014, 53 (5) : 1620–1628. DOI:10.1016/j.isatra.2014.05.007 |