2. 江南大学轻工过程先进控制教育部重点实验室, 江苏 无锡 214122 ;
3. 东南大学自动化学院, 江苏 南京 210000
2. Key Laboratory of Advanced Process Control for Light Industry of the Ministry of Education, Jiangnan University, Wuxi 214122, China ;
3. School of Automation, Southeast University, Nanjing 210000, China
1 引言
感应加热电源对于金属材料加热具有高效、 快速以及低污染的优点被广泛应用于各行各业中,如热加工、 热处理和熔炼等工艺. 传统的感应加热电源由两部分组成,一是用于提供能量的交流电源,一般是工频交流整流后再逆变成可调频的控制部分; 二是实现电磁感应转换为能量的加热部分,通常是固定直径和长度的感应器或感应线圈. 随着加热行业的快速发展,对金属的加热要求也越来越高,不再局限于等温同功率的加热,文[1-2]提出了一种基于温度梯度的感应加热电源,感应线圈由主加热线圈和补温线圈组成,用来克服铝合金等金属在挤压过程产生挤压热造成温度不均带来品质下降的缺点; 文[3-7]从控制方法对感应加热电源进行分析,如模糊PID(proportional-integral-derivative)、 神经网络、 模糊调功以及混合脉冲密度等方法,以达到加热时功率的稳定和最优控制. 文[8]分析了两个感应器的功率耦合控制,消除铝合金梯度加热时两个线圈间磁通的干扰,是对文[1]方法的一个补充. 文[9]对双半桥逆变器部分的耦合感应电源进行了模拟仿真分析,给出了一个在新的控制模式下利用线圈之间的耦合控制输出功率.
本文针对不规则铝合金工件,提出了三段式感应器的感应加热电源,即把传统的固定长度感应器分成三段,分别是主感应加热器、 中间感应加热器和补温感应加热器,这样感应加热电源可以根据铝合金的直径、 长度和规则、 形状等特点智能调整3个感应线圈的相关参数,以实现不同型号、 不同规则铝合金的温度梯度加热. 本文的主要工作: 一是建立感应加热电源的数学模型,利用最小二乘法对被加热金属进行参数辨识得出加热的频率、 时间和功率,从而得知三段感应器的加热参数; 二是针对三段感应器两个工作或者同时工作时,存在磁通的干扰和功率的耦合问题,通过建立等效电路数学模型进行功率解耦,消除线圈之间的耦合影响,从而精确地控制金属在各个感应器所获得的热量,减少能源的损耗,达到最优控制.
2 系统结构多感应器感应加热电源的整体结构如图 1所示,三相电源经过整流后、 电感滤波再逆变分成三路,分别是主加热感应器、 中间加热感应器和补温加热感应器.

|
| 图 1 感应加热电源结构图 Figure 1 Structure of induction heating power |
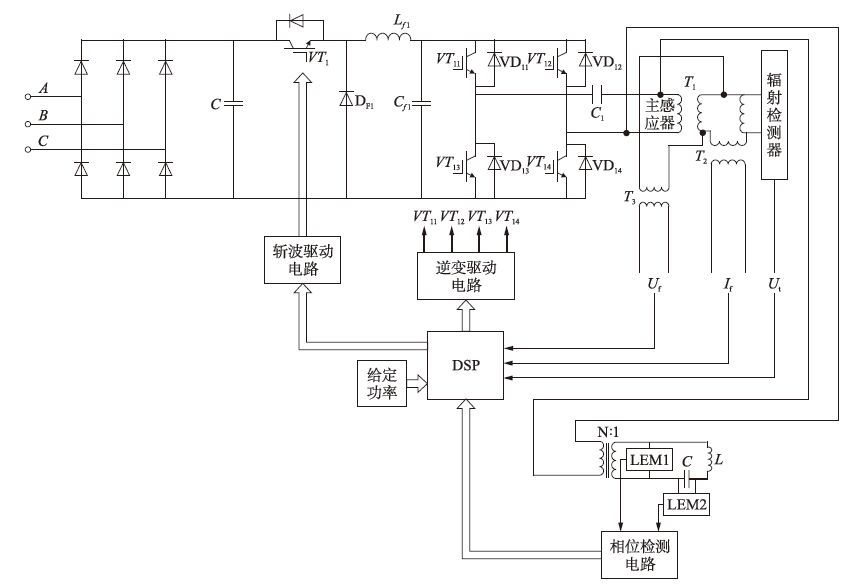
以感应加热电源的主加热感应器为例,其控制方法如图 2所示,分别由辐射检测电路、 相位检测电路、 逆变驱动电路以及斩波驱动电路组成,分段触头电路由多个继电器组成. 该电路能够实时检测主感应器的电压、 电流和磁通等信号,通过DSP(digital signal processing)驱动VT1、 VT11、 VT12、 VT13、 VT14的导通信号,从而控制感应加热电源设计的加热时间、 频率和功率等参数.
|
| 图 2 主感应器控制结构图 Figure 2 Structure of the main inductor |
最小二乘法是系统参数辨识里比较成熟的方法,分为离线辨识和在线辨识两种. 离线辨识是采集到一批数据或者全部数据通过最小二乘估计算法获得系统所需辨识的参数; 在线辨识在系统运行过程中实时采集数据,通过递推最小二乘法辨识相关参数. 铝合金在感应加热电源加热过程中有些参数在不断变化,从而引起其他参数的变化,所以采用在线辨识方法辨识相关参数较为精确. 对于铝合金材料,加热时采用的频率f, 加热时间t, 以及加热功率P是感应加热电源最重要的参数,其数学模型[10]如式(1)~式(3).

|
(1) |

|
(2) |

|
(3) |
式中,ρ0,γ,d, L,T,μ分别为铝合金0 ℃的电阻率(10-6 Ωm),密度(kg·m-3),等效直径(kg·m-3),长度(m),加热温度(℃)和电阻温度系数; μr为相对磁导率; η,t0为感应加热电源加热效率(%)和加热节拍(s); c, λ为平均比热容(J/(kg·℃))和导热系数(w/(m·℃)).
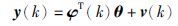
|
(4) |
式(4)中{y(k)}是观测输出序列,{v(k)}是零均值不相关的随机噪声序列,φ(k)∈Rn是观测数据构成的可测信息向量,θ∈Rn是要估计的参数向量. 记:
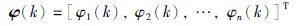
|
(5) |
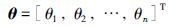
|
(6) |
根据递推最小二乘法的推导得到式(6)~式(8):
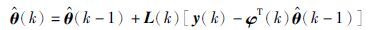
|
(6) |
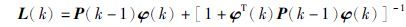
|
(7) |
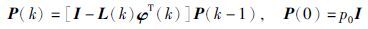
|
(8) |
θ^(k)为时刻k参数向量的θ的估计,L(k)为增量向量,P(k)为协方差矩阵,在算法中,初值P(0)为很大的对称正定阵,p0=106》1,θ^(0)为很小实向量.
取式(4)的最大值,得到式(9):
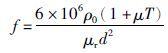
|
(9) |
将式(2)、 式(9)改写成线性回归的形式[13-14],得到式(10):
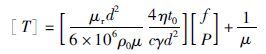
|
(10) |
式(10)中温度T是感应加热电源在加热过程中可以测量的输出变量,功率P和频率f为待辨识参数,然后由式(3)计算出加热时间t. 这样通过不断地在线测量温度T,可以控制铝合金的梯度加热.
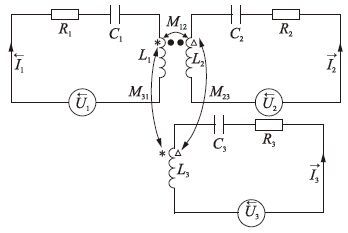
4 功率解耦上述辨识方法经离散后,通过DSP编程实现对应的算法,经过辨识得出的功率P和频率f后,关键是三段感应加热器的功率分配和耦合问题[6]. 根据电磁感应原理,图 1的等效电路可以等效为如图 3所示电压源的控制电路. 其中R1、 R2、 R3分别为各段逆变电路的负载等效电阻,C1、 C2、 C3分别为各段逆变电路的谐振电容,L1、 L2、 L3分别代表逆变电路的等效电感,M12、 M13、 M23三段电感间的互感.
|
| 图 3 加热电源的等效电路 Figure 3 Equivalent circuit of heating power |
根据耦合电路分析原理,令I1=I1(cos φ1+jsinφ1),I2=I2(cos φ2+jsinφ2),I3=I3(cosφ3+jsin φ3),U1=U1(cos θ1+jsin θ1),U2=U2(cos θ2+jsin θ2),U3=U3(cos θ3+jsin θ3); φ1,φ2,φ3,θ1,θ2,θ3分别为I1,I2,I3,U1,U2,U3的相位角,I1,I2,I3,U1,U2,U3为I1,I2,I3,U1,U2,U3的幅值.
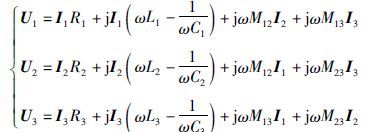
|
(11) |
以主感应器逆变电路为例,求解功率得到式(12):

|
(12) |
化简得到式(13):

|
(13) |
同理,可以求得中间感应器和补温感应器的逆变电路功率,见式(14)和式(15):
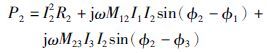
|
(14) |
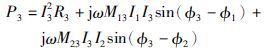
|
(15) |
从式(13)~式(15)可以发现,只要φ1=φ2=φ3,逆变器输出功率P1=I21R1,P2=I22R2,P3=I23R3,实现了主感应器线圈、 中间感应器线圈和补温感应器线圈输出功率之间的解耦. 同理可以推广到多个感应器的解耦方法,充要条件是各个感应器的逆变电路的电流输出相位相同.
5 仿真与实验结果按照图 1和图 2方式搭建了一台由3个感应器组成的感应加热炉的电源仿真模型,以牌号6A02的铝合金为例,首段规格:φ80 mm×45 mm; 质量: 5.662 kg; 加热温度: 480+10-20℃; 加热节拍: ≤30 ℃. 代入式(9)得到:

|
这里求得f=150.562 5 Hz, 取150 Hz. 功率由式(2)得到:
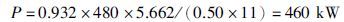
|
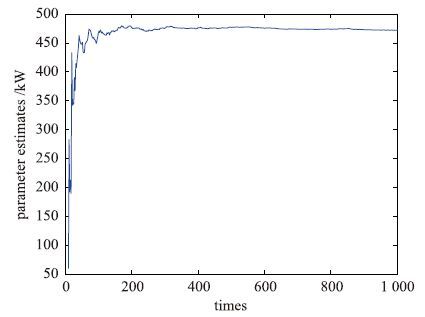
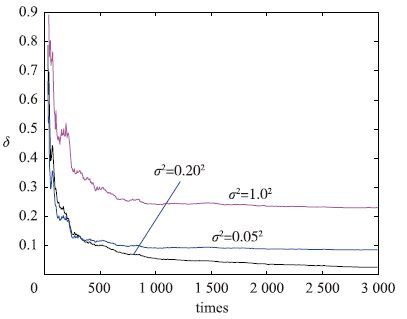
通过Matlab仿真模型得到参数辨识递推曲线如图 4和图 5所示,反应了系统的加热频率和功率分别在递推300次和1 000次后达到了允许的误差. 其中图 4的频率参数稳定在155 Hz, 与式(9)计算的实验数值150 Hz, 误差为3.33%; 图 5的功率参数稳定在475 kW,与式(10)计算出的实验数值460 kW,误差为3.26%,误差比小于5%,在要求的误差范围以内,同时根据图 6的不同噪声方差下的估计误差,进一步验证了模型的正确性.

|
| 图 4 频率参数辨识递推曲线 Figure 4 Recursive curve of frequency parameter identification |
|
| 图 5 功率参数辨识递推曲线 Figure 5 Recursive curve of power parameter identification |
|
| 图 6 不同噪声方差下的估计误差 Figure 6 Estimation error under different noise variance |
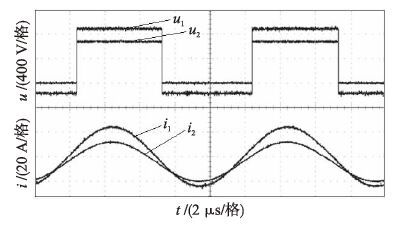
按照上述理论分析,研制了一台功率10 kW的样机,加热的金属工件规格为的铝合金,根据辨识方法得出的加热频率为10 kHz. 图 7和图 8是感应加热电源第1个感应器和第2个感应器的逆变器输出电压和电流波形.
从图 7中可以发现,感应器间由于未采用电流同相,感应器线圈存在耦合现象; 图 8是采用电流同相控制,感应器逆变输出电压和电流相位差为零. 逆变器的输出参数分析见表 1.

|
| 图 7 未解耦时电压电流波形 Figure 7 Voltage and current waveform without decoupled control |
|
| 图 8 解耦时电压电流波形 Figure 8 Voltage and current waveform with decoupled control |
| 输出参数 | 耦合控制时 | 解耦控制时 | ||
| 逆变器1 | 逆变器2 | 逆变器1 | 逆变器2 | |
| 电压/V | 470 | 310 | 460 | 300 |
| 电流/A | 22 | 15 | 21.5 | 14 |
| 功率/kW | 10.34 | 4.65 | 9.89 | 4.2 |
从表 1的数据中可以发现耦合控制和解耦控制时,逆变器1和逆变器2的电压、 电流和功率都有下降,其中功率分别下降4.35%和9.68%. 原因是实现了感应加热电源的解耦,从而消除了互感线圈产生的功率,实现加热电源的节能控制.
6 结论本研究针对当前加热行业需要实现金属的梯度加热和不规则金属的分段补温加热等要求,提出了一种分段式多感应器加热电源. 根据加热模型,利用参数辨识方法,根据工件的材料、 直径和长度等特点辨识出金属工件的加热功率、 时间和频率,达到感应加热电源功率的实时可调; 并基于等效电路模型消除了多感应器线圈间的耦合现象,实现了感应加热电源功率最大化,在仿真模型和实验样机得到了验证,为感应加热电源的分段和联合控制提供参考.
| [1] | 刘晓辉, 张振世. 一种有温度梯度的感应加热设备[J]. 工业加热 , 2010 (5) : 51–52. Liu X H, Zhang Z S. An induction heating equipment of temperature gradient aluminum alloy tube[J]. Industrial Heating , 2010 (5) : 51–52. |
| [2] | 赵飞, 耿程飞, 张永亮. 基于 LLC 的梯度加热电源研究[J]. 电源技术 , 2013, 37 (11) : 2044–2046. Zhao F, Geng C F, Zhang Y L. Study on gradient heating power based on LLC[J]. Chinese Journal of Power Sources , 2013, 37 (11) : 2044–2046. |
| [3] | 吴延华, 娄丽丽, 索红亮. 基于模糊神经网络的中频感应加热电源的研究[J]. 机械制造与自动化 , 2011, 40 (3) : 110–112. Wu Y H, Lou L L, Suo H L. Fuzzy neural network based on medium frequency induction heating power supply[J]. Machine Building & Automation , 2011, 40 (3) : 110–112. |
| [4] | 惠晶, 肖进. 基于模糊调功的感应加热电源研究[J]. 金属热处理 , 2008, 33 (10) : 84–87. Hui J, Xiao J. Induction heating power supply based on fuzzy power modulation[J]. Heat Treatment of Metals , 2008, 33 (10) : 84–87. |
| [5] | 彭咏龙, 李荣荣, 李亚斌, 等. 基于 HPDM 的感应加热电源功率调节技术[J]. 电气传动 , 2013 (1) : 171–174. Peng Y L, Li R R, Li Ya B, et al. Power regulation technology of induction heating power supply based on HPDM[J]. Electric Drive , 2013 (1) : 171–174. |
| [6] | Forest F, Labouré E, Costa F, et al. Principle of a multi-load/single converter system for low power induction heating[J]. IEEE Transactions on Power Electronics , 2000, 15 (2) : 223–230. DOI:10.1109/63.838094 |
| [7] | Umasankar P, Kumar S S. Neuro-fuzzy logic control of single phase matrix converter fed induction heating system[J]. Research Journal of Applied Sciences Engineering & Technology , 2015, 9 (6) : 419–427. |
| [8] | 胡程平, 陈辉明. 多感应器感应加热电源功率解耦控制[J]. 电力电子技术 , 2012, 46 (4) : 10–11. Hu C P, Chen H M. Multi-inductor power decoupled control in induction heating power supply[J]. Power Electronics , 2012, 46 (4) : 10–11. |
| [9] | Booma N, Reddy S R, Pradeep V. Simulation of PWM controlled double half bridge inverter for partly coupled induction cooking system[M]. Berlin, Germany: Springer , 2015 : 237 -244. |
| [10] | 李韵豪. 锻压工业中的感应加热——第五讲 铝合金的感应加热及感应器的设计与参数计算[J]. 机械工人: 热加工 , 2007 (6) : 85–90. Li Y L. Induction heating forging industry-aluminum induction heating and sensor design and parameter calculation[J]. Machinist Metal Forming , 2007 (6) : 85–90. |
| [11] | 庞强, 夏琼, 邹涛, 等. 一种基于模型参考自适应辨识的半自动模型预测控制方法[J]. 信息与控制 , 2014, 43 (6) : 681–689. Pang Q, Xia Q, Zhou T, et al. The semi-automatic model predictive control method based on model reference adaptive identification algorithm model reference adaptive identification algorithm[J]. Information and Control , 2014, 43 (6) : 681–689. |
| [12] | 丁锋. 系统辨识新论[M]. 1版. 北京: 科学出版社 ,2013 : 45 -65. Ding F. System identification[M]. 1版. Beijing: Science Press , 2013 : 45 -65. |
| [13] | 苏奇全, 贾宏光, 朱明超, 等. 基于递推闭环子空间辨识的自适应预测控制方法[J]. 信息与控制 , 2015, 44 (2) : 252–256. Su Q Q, Jia H G, Zhu M C, et al. An adaptive predictive control method based on recursive closed-loop subspace identification[J]. Information and Control , 2015, 44 (2) : 252–256. |
| [14] | 王佳, 王宏伟, 夏浩, 等. 基于子空间的多率控制系统闭环辨识[J]. 信息与控制 , 2014, 43 (5) : 583–587. Wang J, Wang H W, Xia H, et al. Subspace-based closed-loop identification of multirate control system[J]. Information and Control , 2014, 43 (5) : 583–587. |



