2. 中国石油天然气股份有限公司辽河石化分公司仪电运行部
2. Meter Running Department, Liaohe Petrochemical Industries Co. of Petro China Co. Ltd
1 引言
支持向量机通常仅需要少量样本进行学习,且支持向量占学习样本的较小部分,但其不具备增量学习能力. 增量学习在充分利用历史数据的基础上,能提高训练速度. 若将支持向量机与增量学习相结合,可以解决传统支持向量机在新加入样本后需要消耗大量时间重新训练的问题. Peng等人总结PAR-V-SVC[1]和TSVM[2]的特点,提出了参数间隔孪生支持向量机[3]. 它通过求解一对对偶问题,从而求出正、 负类两个不平行的分类超平面,再由这一对超平面求解出最优分类超平面. 它具有比传统支持向量机更快的运算速度和更高的准确率.
相关研究也提出了一系列关于传统支持向量机的增量算法,主要分为三大类: Batch SVM增量算法[4]: 该方法每次训练结果只保留支持向量参与到下次增量学习中,但其忽略了非支持向量的作用; 基于错误驱动增量学习算法: 该方法保留支持向量和错分样本参与到下次训练中,却忽略了被分类正确样本中非支持向量的作用; 基于KKT条件的增量学习算法: 通过判断新增样本是否满足KKT条件所对应的数值条件,决定样本是否参与到下次训练中,该方法虽然同时考虑到了原样本和新增样本是否满足最终分类器的KKT条件,但最终因满足KKT条件而被舍弃的部分样本可能包含下次增量学习所需信息. 一些学者针对上述增量算法的缺点,提出了改进的增量学习算法,如王晓丹等人提出的一种新的SVM对等增量学习算法[5],该算法对新增样本与原始样本同时训练,再用得到的分类器对数据进行判别,从而获得最终分类所用信息. 该算法主要作用是剔除新增样本附近冗余信息. 曹建等人提出的基于KKT条件的SVM增量学习算法[6],分析了在新加入样本后,新分类的分类平面所在范围及变化趋势. 朱发等人提出了一种基于最小样本平面距离的支持向量增量学习算法[7],文[5-6]在对基于KKT条件的增量算法分析的基础上,研究了如何更加合理地对新增数据进行取舍.
虽然TPMSVM拥有较快的运算速度,但面对大量历史数据时,仍然需要较长时间处理,且目前还没有基于TPMSVM的增量算法相关的文献. 本文首先通过对参数间隔孪生支持向量机的KKT条件证明,找到样本满足TPMSVM的KKT条件所对应的数值条件,然后分别引入松弛因子ε和数据约减因子d,进一步提高基于TPMSVM的增量算法的训练速度及准确率. 最后根据TPMSVM特点提出适用于它的增量学习算法.
2 参数间隔支持向量机线性可分训练数据集为T={(xi,yi)i=1,2,…,m},输入x∈Rn,y∈{-1,+1}为相应的输出. m1个正类样本记为X1∈Rm1×n,m2个负类样本记为X2∈Rm2×n,n维状态空间内,找到两个不平行的超平面:
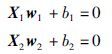
|
(1) |

|
(2) |

|
(3) |
式中,c1,c2,v1,v2为正的参数,e=(1,…,1)T.
式(2)的目标函数的第一项正则项表示结构最小化,第二项表示代表其中一类别的平面最大程度的远离另一类别,第三项表示松弛度即允许出现的误差,约束条件表示属于本类别的样本要在该平面的左侧,式(3)同理.
式(2)、 式(3)对偶问题可以用下式表示:
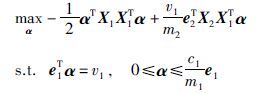
|
(4) |
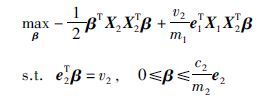
|
(5) |
相应的α∈Rm1,β∈Rm2为拉格朗日乘子. 非平行的一对平面可由式(4)、 式(5)解出α、 β求得.
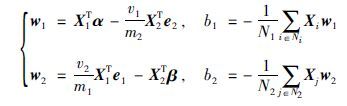
|
(6) |
N1,N2分别为正负分类平面支持向量个数,最终判别函数为
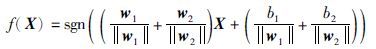
|
(7) |
由决策函数可知: 需同时计算样本到两超平面的距离,才能决定样本属于哪一类,这是它与传统支持向量机在决策函数上最大的不同.
对于线性不可分情况,它与传统支持向量机一样引入核函数,把输入X映射到高维空间中得到Φ(X). 相应的非线性形式可用下式表达:
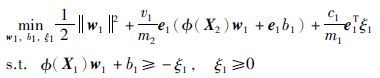
|
(8) |
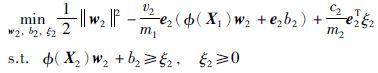
|
(9) |
相应的对偶形式为
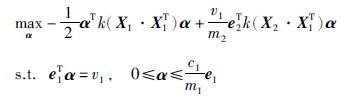
|
(10) |
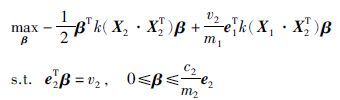
|
(11) |
同理可求得w与b的值如下式:

|
(12) |
定理 设α*为式(10)的解,则α*j=0,对应的样本分布在正类分类平面正的一侧; α*j=c1/m1,对应样本分布在正分类平面负一侧或错分;0 <α*jc1/m1对应样本分布在正分类平面上. 则下式成立:

|
对应样本分布在负分类平面上:
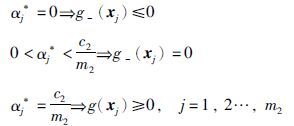
|
证明 正类分类平面KKT条件证明: 由式(10)可知正类分类超平面可用下式表示:
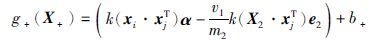
|
(13) |
令H1=k(xi·xj)m1×m1,H2=k(X2·xj)m1×m2
其中e=(1,…,1)T,α=(α1,…,αi).
把(10)式改写为如下形式:
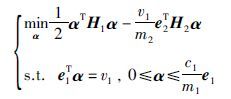
|
(14) |

|
(15) |
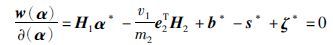
|
(16) |
则式中α*为式(14)的解条件为,拉格朗日系数b*,ζ*,s*,满足下式关系:

|
(17) |
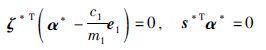
|
(18) |
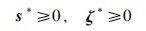
|
(19) |
由式(17)、 式(19)可知:
因为:
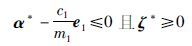
|
所以:
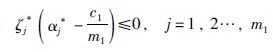
|
又由式(18)知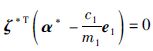
所以:
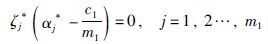
|
(20) |
同样,由于α*≥0且s*≥0
由式(18)知
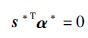
|
(21) |
所以:s*jα*j=0,j=1,2…,m1
① 当α*j=0时,由式(18)知: ζ*j=0,代入式(15)可得:
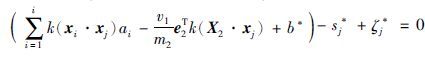
|
所以:g+(X+)=s*j≥0,j=1,2…,m1
② 当0 <α*jc1/m1时,由式(20)、 式(21)知:

|
所以: g+(X+)=0,j=1,2…,m1
③ 当α*j=c1/m1时,由(21)知: s*j=0
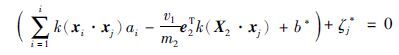
|
所以: g+(X+)=-ζj*≤0,j=1,2…,m1
证毕.
当分类平面为负时有类似证明,这里不再赘述.
基于KKT条件的传统支持向机增量算法,在进行增量训练时正负样本不作区分,同时放入正负增量样本,即可得到需保留的训练数据. 参数间隔孪生支持向量机与传统支持向量机最大的不同在于它构造了一对相互不平行的超平面,两超平面都需求解出. 参数间隔孪生支持向量机在进行增量学习时,正类样本需要代入正类分类平面中进行判别,负类样本代入负类分类面中判别.
4 TPMSVM增量学习算法增量学习关键步骤是找到使分类平面变化的样本,通过上面的分析可知: 新增正类样本中符合g+(x+) <0则表明样本在分类间隔内或错分,这些样本可能改变分类平面,即违背KKT条件的样本点. 而当g+(x+)≥0时,表明这类样本在原正分类平面上或正的一侧,不会改变分类平面的位置. 负类时同理. 当新增样本使分类平面发生改变时,原始数据中非支持向量也可变为支持向量. 随着新增数据加入,分类平面变化如图 1所示.
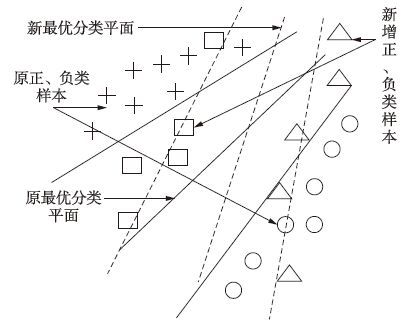
|
| 图 1 新增样本对分类平面影响 Figure 1 Effect of new sample on classification plane |
原训练样本中一些数据并不包含下次分类的必要信息[5]. 去除原始训练数据中非必要分类信息可以加快训练速度,而保留新增信息中的必要分类信息又是保证分类精度的关键. 一些相关文献对如何合理地去除增量学习过程中的冗余数据作了研究[8-10].
针对原训练样本,首先得到其分类平面,保留离分类平面距离较近的数据,因为这些离分类面比较近的非支持向量也可能转化为支持向量. 这样既可以达到数据约简的目的,又可以保存分类回归所必须的数据. 设定合理的d值,可以达到上述目的. 计算点到平面的公式如下:
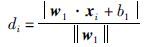
|
(12) |
式中w1和b1可通过式(12)得到可由式(22)计算出所有原始训练样本到分类平面的距离,然后求出平均距离daveragr最远距离dmax,d+在这两个值间取值,约减掉大于d+所对应的数据,负类时同理可得.
由图 1可知: 仅仅考虑增量样本中违背KKT条件的样本是不合理的. 增量数据中除了违反KKT条件,其附近数据也包含新的分类平面一些特征信息[11]. 这部分样本满足KKT条件样本但与原分类面间隔比较近. 对于新增样本可设定广义KKT条件[12],对于正类通过判断g+(x+)≤0+ε,ε≥0来确定新增样本是否参加训练. ε的大小决定参加训练新增样本的多少. 负类时判别条件: g-(x-)≥0+ξ,ξ≤0.
参数ε的取值取决于新增样本靠近原分类平面的程度. 对于在正分类平面左侧的样本,式子f(x)=wixi+bi的值为正,在其右侧样本对应的值为负值,而右侧的值已通过KKT条件选出作为训练集,所以不需考虑. 只需计算左侧数据在正分类平面的分布即可. 利用式(22),但需要去除wixi+bi的绝对值符号,以便区分数据在左侧还是右侧,只计算结果为正的增量数据到正分类平面的平均距离dg,一般取1/4dg到1/2dg之间的值即可,负类同理.
具体增量学习步骤如下:
步骤1: 训练原始样本得到正、 负类分类器g+(x),g-(x).
步骤2: 设定d+、 d-值,得到参加分类器训练的原始数据,并验证分类正确率,正确率不变或下降不大则不需调整d+的值,相反则需要调整. 由此步骤得到约减后的训练数据集,这些数据中包含着支持向量.
步骤3:设定ε、 ξ值,正类增量样本输入到由原始数据集训练得到的正分类器g+(x)中,选出违背广义KKT条件的样本,然后将这些选出的增量数据放入由步骤2得到的训练样本中,一起训练得到新的正类分类器g+(x),负类同理. 如果没有违背KKT条件数据则转到步骤4.
步骤4: 没有违背广义KKT条件样本,则原分类器不改变. 进入下一次增量训练.
每到来一批新的数据,则执行步骤2~4一次,得到新的正、 负类分类器.
5 实验数据及手段本文采用UCI数据库balance[13]和letter[14]数据进行验证,balance数据集为3分类,共625个数据,左类290个,右类288个,平衡类49个. 取左类160个数据作为负类训练数据,取右类160个,平衡类25个数据作为正类训练数据. 剩余280个样本数据作为验证样本. letter数据集中选取A,B,C为正类,D,E为负类. 按1∶1的比例选取1 000个训练数据和800个测试数据. 依据经验两组测试数据都进行5次等量增量训练,数据如表 1、2.
| 算法 | 对比算法 | 本文算法 | 非增量法 | |||
| 类别 | 正类 | 负类 | 正类 | 负类 | 正类 | 负类 |
| 初始数量 | 40 | 40 | 40 | 40 | 40 | 40 |
| 增量数量 | 29 | 24 | 29 | 24 | 0 | 0 |
| 测试数量 | 280 | 280 | 280 | |||
| 算法 | 对比算法 | 本文算法 | 非增量法 | |||
| 初始数量 | 150 | 100 | 150 | 100 | 150 | 100 |
| 增量数量 | 90 | 60 | 90 | 60 | 0 | 0 |
| 测试数量 | 800 | 800 | 800 | |||
为了体现所提出的增量算法在约减数据的同时扩展KKT条件的优越性,本文参照传统基于SVM的KKT增量算法原理并对其进行一定改进,分别利用TPMSVM和SVM设计了一种对比增量方法,并分别得到对比增量法1和对比增量法2,同时与基于TPMSVM的非增量法进行对比. 步骤如下:
步骤1:训练原始样本得到正、 负类分类器g+(x),g-(x).
步骤2: 找出违背KKT条件的数据,并与原始数据合并形成新的训练集并训练,得到新的分类器. 如果没有违背KKT条件数据则转到步骤3.
步骤3: 没有违背广义KKT条件样本,则原分类器不改变. 进入下一次增量训练.
每到来一批新的数据,则执行步骤2~3一次,得到新的正、 负类分类器.
6 实验结果及分析本文仿真实验在Matlab 8.1环境下编程实现,采用径向基核函数.
因为本文所用初始样本是整个样本集中很小一部分,同时本文所提算法中每次保留数据时d+的取值不同,所以算法所用时间随增量次数出现增加的现象.
由图 2及表 3各算法的balance数据集对比结果可以看到,保留原数据集的有效信息,除去无用数据可加快训练速度,对比增量法1和本文增量法精确度相当,但本文增量方法速度更快. 在样本维数较低的情况下,对比增量法1虽然所用训练时间比对比增量法2多,但精度上对比增量法2更高,这说明在正、 负训练样本不均衡情况下利用TPMSVM可获得更高的准确率. 本文增量方法在保持一定精度同时,相比非增量法节约了大量训练时间. 由于过多增量数据进入分类间隔内,使模型泛化性能有所降低,所以这几种方法不同程度地出现了随着增量次数的增加准确率降低的现象.
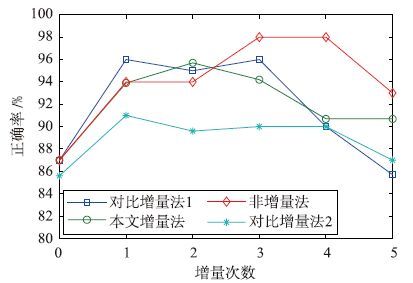
|
| 图 2 balance数据正确率对比图 Figure 2 Comparison of balance data correct rate |
| 算法 | 对比增量法1 | 对比增量法2 | 本文增量法 | 非增量法 |
| 初始样本 | 0.23 s | 0.22 s | 0.23 s | 0.23 s |
| 增量1 | 0.4 s | 0.4 s | 0.17 s | 0.5 s |
| 增量2 | 0.5 s | 0.5 s | 0.27 s | 0.7 s |
| 增量3 | 0.8 s | 0.6 s | 0.23 s | 0.9 s |
| 增量4 | 0.9 s | 0.62 s | 0.3 s | 1.4 s |
| 增量5 | 1.15 s | 0.64 s | 0.29 s | 2.1 s |
由图 3及表 4各算法letter数据集实验结果可知: 对比增量法1所用训练时间比本文增量法要少,这是由于利用狭义KKT条件判别的数据中,极少新增数据被利用到下次训练,新增数据中很大一部分有效数据被遗失,导致正确率不能随新增数据加入有所提高. 本文增量法利用广义KKT条件弥补这一缺陷,其能使有效新增数据进入训练,从而提高分类准确率. 狭义KKT条件存在局限性的原因是没有考虑证明过程中拉格朗日子ζ和s的影响. 广义KKT条件中松弛因子ε和ξ的引入弥补了这一缺陷,因此明显提高了分类精度. 对比增量法2与非增量法对比可以看出: TPMSVM在处理高维度且正、 负训练样本不均衡情况的大量样本的训练比传统SVM拥有更快的训练速度和更高的准确率. balance数据和letter数据这两个实验对比也间接说明增量数据在一定的数量和维数内,增量次数的多少不会对准确率造成较大影响.
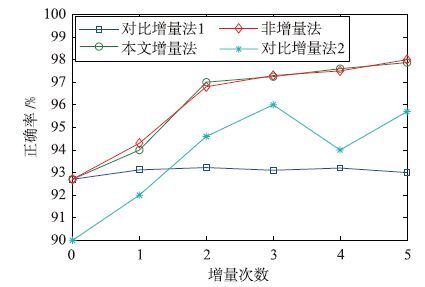
|
| 图 3 letter数据正确率对比图 Figure 3 Comparison of letter data correct rate |
| 算法 | 对比增量法1 | 对比增量法2 | 本文增量法 | 非增量法 |
| 初始样本 | 1.4 s | 1.8 s | 1.4 s | 1.4 s |
| 增量1 | 1.08 s | 3.5 s | 3.1 s | 3.3 s |
| 增量2 | 1.6 s | 3.8 s | 3.3 s | 6.2 s |
| 增量3 | 1.5 s | 6.8 s | 4.8 s | 12.6 s |
| 增量4 | 1.6 s | 430 s | 5.6 s | 190 s |
| 增量5 | 1.6 s | 750 s | 6.3 s | 69 s |
本文由TPMSVM的KKT条件证明入手,并对KKT条件进行合理扩展,提出了一种适用于TPMSVM的增量算法,该算法选取新增数据中违背广义KKT条件和部分满足条件原始数据参加分类器的训练. 针对初始训练样本与增量样本相差不大的增量学习问题,该算法的仿真获得了较好的验证结果,即该算法在保持一定分类精度的前提下,提高了TPMSVM训练速度. 如何更加准确地确定广义KKT条件参数ε的取值是下一步研究的重点.
| [1] | Hao P Y. New support vector algorithms with parametric insensitive/margin model[J]. Neural Networks , 2010, 23 (1) : 60–63. DOI:10.1016/j.neunet.2009.08.001 |
| [2] | Khemchandani J R, Chandra S. Twin support vector machines for pattern classification[J]. Pattern Analysis and Machine Intelligence , 2007, 29 (5) : 905–910. DOI:10.1109/TPAMI.2007.1068 |
| [3] | Xin J P. TPMSVM: A novel twin parametric-margin support vector machine for pattern recognition[J]. Pattern Recognition , 2011, 44 : 2678–2692. DOI:10.1016/j.patcog.2011.03.031 |
| [4] | Syed N, Sung K. Handling concept drifts in incremental learning with support vector machines[C]//Proceedings of the 5th ACM SIGKDD International Conference. New York, NY, USA: ACM, 1999: 316-321. http://cn.bing.com/academic/profile?id=2078382802&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] | 王晓丹, 郑春颖, 吴崇明, 等. 一种新的SVM对等增量学习算法[J]. 计算机应用 , 2006, 26 (10) : 2440–2443. Wang X D, Zheng C Y, Wu C M, et al. New algorithm for SVM-based incremental learning[J]. Computer Applications , 2006, 26 (10) : 2440–2443. |
| [6] | 曹健, 孙世宇, 段修生, 等. 基于KKT条件的SVM增量学习算法[J]. 火力与指挥制 , 2014 (7) : 139–143. Cao J, Sun S Y, Duan X S, et al. SVM incremental learning algorithm based on KKT conditions[J]. Fire Control & Command Control , 2014 (7) : 139–143. |
| [7] | 朱发, 业宁, 潘冬寅, 等. 基于最小样本平面距离的支持向量机增量学习算法[J]. 计算机工程与设计 , 2012, 33 (1) : 346–350. Zhu F, Ye N, Pan D Y, et al. Incremental support vector machine approach based on minimum sample plane distance[J]. Computer Engineering and Design , 2012, 33 (1) : 346–350. |
| [8] | 萧嵘, 王继成. 一种SVM增量学习算法α-IsvM[J]. 软件学报 , 2011, 12 (12) : 818–824. Xiao R, Wang J C. An SVM incremental learning algorithm for α-IsvM[J]. Software Journal , 2011, 12 (12) : 818–824. |
| [9] | 孔波, 刘小茂, 张钧. 基于中心距离比值的增量学习算法[J]. 计算机应用 , 2006, 26 (6) : 1434–1436. Kong B, Liu X M, Zhang J. Incremental learning algorithm based on central distance ratio[J]. Computer Application , 2006, 26 (6) : 1434–1436. |
| [10] | 申骁勇, 雷英杰. 一种SVM增量学习淘汰算法[J]. 计算机工程与应用 , 2007, 43 (6) : 171–173. Shen X Y, Lie Y J. Sifting algorithm for incremental SVM learning[J]. Computer Engineering and Application , 2007, 43 (6) : 171–173. |
| [11] | 张灿淋, 姚明海, 童小龙, 等. 一种新的基于KKT条件的错误驱动SVM增量学习算法[J]. 计算机系统应用 , 2014 (1) : 144–148. Zhang C L, Yao M H, Tong X L, et al. A new error-driven incremental SVM learning algorithm based on KKT conditions[J]. Application of Computer System , 2014 (1) : 144–148. |
| [12] | 赵莹, 万福永. 支持向量机的增量学习算法及其在多类分类问题中的应用[C]//第25届中国控制会议论文集(下册). 北京: 中国自动化学会控制理论专业委员会, 2006: 4. Zhao Y, Wan F Y. The incremental learning algorithm of support vector machine and its application in multi class classification problems[C]//Proceedings of the Twenty-fifth Conference in China Control (2). Beijing: China Automation Society Control Theory Professional Committee, 2006: 4. |
| [13] | Hume T. Balance scale weight & distance database[EB/OL]. [2015-06-13]. http://archive.ics.uci.edu/ml/datasets/Balance+Scale. |
| [14] | Slate D J. Database of character image features; try to identify the letter[EB/OL]. [2015-6-13]. http://archive.ics.uci.edu/ml/datasets/Letter+Recognition. |



