1 引言

1971年，美国华裔科学家Leon Chua基于对称性原理，预测除了电阻、 电容和电感三种无源基本电路元件之外，还应该存在第4种无源电路基本元件——忆阻器^[1]. 2008年，惠普实验室成功研制出了固态忆阻器，并将成果发表在《Nature》杂志上^[2]. 由于忆阻器具有记忆特性、 纳米尺度、 模拟神经突触等特点，使得忆阻器在人工神经网络、 保密通信、 存储器、 人工智能计算机等新兴信息技术领域都有潜在的应用前景^[2-7].

由于忆阻器神经网络在图像处理、 优化问题、 线性规划等方面都有广泛的应用. 近年来，忆阻器神经网络的动态特性和应用受到很多学者的关注，如稳定性、 耗散性、 周期振荡等，并且取得了许多科研成果^[8-10]. 文^[8]利用非光滑分析、 李亚普诺夫函数及不等式的方法分析了忆阻器递归神经网络的全局一致稳定性. 文^[9]基于M矩阵理论和LaSalle不变集理论，研究了忆阻器神经网络的耗散性. 文^[10]采用了集值分析中的拓扑度理论，微分包含理论和李亚普诺夫函数方法，探讨了忆阻器神经网络的周期动态性.

同步性是忆阻器神经网络动态特性中最重要的特性之一. 文^[11]研究了基于周期性间歇控制忆阻器神经网络的指数同步，采用非光滑分析、 李亚普诺夫函数及不等式的方法，获得了指数同步的充分条件. 文^[12]基于驱动—响应概念和微分包含的理论，研究了混沌忆阻器神经网络的全局反同步. 文^[13]采用了非光滑分析和李亚普诺夫函数，研究了忆阻器递归神经网络的延迟同步.

可见，研究忆阻器神经网络的同步性问题，非光滑分析的方法应用非常广泛. 从上述文献中可知，忆阻器神经网络的同步、 反同步和延迟同步都有相关的研究，但是对于忆阻器神经网络延迟反同步的研究并不多. 文^[14]采用了李亚普诺夫函数的方法，研究了超混沌复杂系统的延迟反同步. 反同步控制已经成功地应用到很多领域，如图像处理、 信息科学等^[15-16]. 延迟同步控制在保密通信中也有很大的应用前景^[17]. 在通信系统中通过应用反同步控制，就可以在同步与反同步之间连续地传送数字信号，这就增强了通信系统中的安全性与保密性^[12]. 而延迟反同步也属于反同步，因此延迟反同步的研究具有重要的意义.

本文在前人研究的基础上，对忆阻器神经网络的模型作了描述，并基于非光滑分析和控制理论，研究了混沌忆阻器神经网络的延迟反同步. 同时在文^[11]的基础上，对充分性判据作了推广，使得定理不仅适用于反同步，也同样适用于延迟反同步，从而有助于推动忆阻器神经网络的延迟反同步研究.

2 系统模型

考虑如下具有时滞的混沌忆阻器神经网络^[18]：

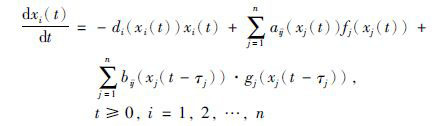
(1)

其中，x_i(t)是第i个神经元的状态变量，d_i(x_i(t))表示自反馈变量，a_ij(x_j(t))和b_ij(x_j(t-τ_j))是连接权值，τ_j为时滞且满足max_jτ_j=τ，f_j(·)和g_j(·)为激活函数. 传统的神经网络权值采用的是电阻，而上述神经网络的权值采用的是忆阻器. 根据忆阻器的特点，将这些权值表示为

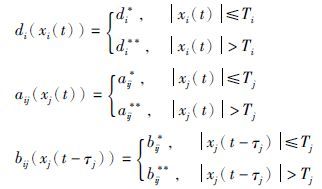
(2)

式中，d^*_i ＞0、 d^**_i＞0、 a^*_ij、 a^**_ij、 b^*_ij和b^**_ij都是常数，T_j＞0，i, j=1，2，…，n.

将系统(1)作为驱动系统，其相应的响应系统为^[18]

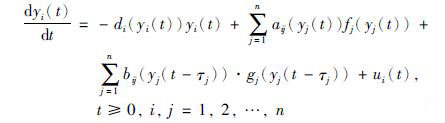
(3)

同理，将系统(3)的权值表示为

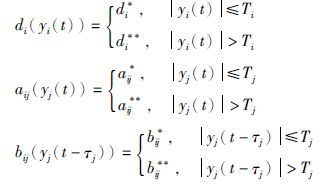
(4)

本文的目标是设计合适的控制器使得驱动系统与响应系统能够实现延迟反同步. 考虑线性反馈控制器：

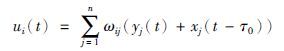
(5)

式中，ω_ij为控制器增益且Φ=(ω_ij)_n×n是一个常数矩阵，i, j=1，2，…，n, τ₀为延迟时滞且τ₀ ＞0.

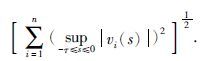
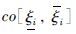
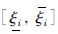
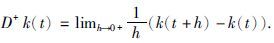
在本文中，所有系统的解都是在Filippov意义下的^[19]. 在Banach空间中，对于v_i(s)∈C([-τ，0]，R)，定义||v||_c=对于所有的连续函数C((-τ，0)，Rⁿ)，在Banach空间中，表示为的凸面. 对于一个连续函数k(t)∶R→R，D⁺k(t)被称为右上Dini导数而且被定义为 系统(1)和系统(3)的初始条件分别为x_i(s)=φ_i(s)，y_i(s)=ψ_i(s)，φ_i(s)，ψ_i(s)∈C([-τ，0]，R)，i=1，2，…，n.

应用微分包含和集值映射^[19-20]的理论，系统(1)可以描述为

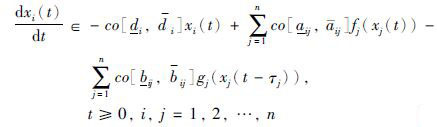
(6)

同理，系统(3)也可以描述为

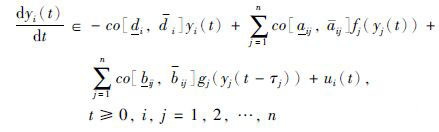
(7)

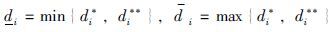
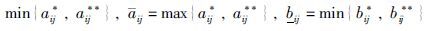
其中，，a_ij=，b_ij=max｛b^*_ij，b^**_ij｝.

记e_i(t)=y_i(t)+x_i(t-τ₀)，由式(6)、 (7)可以得到下面的同步误差系统：

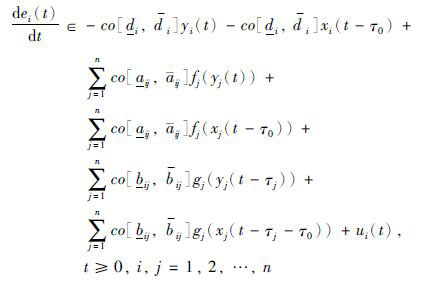
(8)

若D∈co[d_i，d_i]，A∈co[a_ij，a_ij]，B∈co[b_ij，b_ij]，那么上式也可以表示为

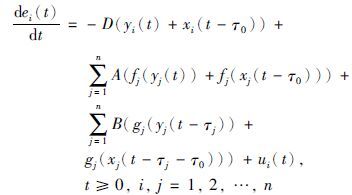
(9)

假设1 对于∀s₁，s₂∈R，j=1，2，…，n, 神经元激活函数f_j，g_j是Lipschitz连续的，满足以下不等式：

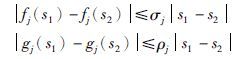
(10)

其中，s₁≠s₂，σ_j、 ρ_j是非负常数.

定义1^[21] 对于任意的φ=(φ₁(t)，φ₂(t)，…，φ_n(t))，ψ(t)=(ψ₁(t)，ψ₂(t)，…，ψ_n(t))∈C([-τ，0]，Rⁿ)，如果存在常数M≥1和μ ＞0，使得不等式e(t)²≤Mψ(t)+φ_τ0²_cexp(-μ(t-τ₀))(t≥τ₀)成立，其中μ为延迟反同步率，φ_τ0为x(t)在t≥τ₀时的初始向量，那么驱动系统(1)与响应系统(3)实现指数延迟反同步.

引理1^[22] 对于-∞ ＜a＜b≤+∞，若z_i(t)∈C([a, b)，R)(i=1，2，…，n)且z_i(t)满足下面的积分延迟不等式：

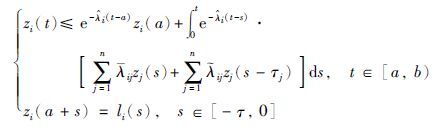
其中，0≤τ_j≤τ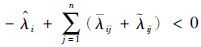，$\hat \lambda $_i、λ_ij和$\hat \lambda $_ij是正数，且假设$\hat \lambda $_i、λ_ij、$\hat \lambda $_ij和z_i(t)满足与z_i(t)≤T||l||_c²(t∈[a-τ，a]，i=1，2，…，n)，则z_i(t)≤Tl²_c，t∈(a, b)，其中T ＞0且是一个正常数，i=1，2，…，n.

引理2^[12](Halanay不等式) 如果τ≥0且τ为常数，在[-τ，+∞)上，ν(t)是一个非负的函数且ν(t)满足： dν(t)dt≤-aν(t)+b(supt-τ≤s≤tν(s))，t≥0，式中a. ＞b＞0，那么ν(t)≤(sup-τ≤s≤0ν(s))exp(-θt)，t≥0，其中θ为有界的收敛率且唯一的正数解为θ=a-bexp(θτ).

引理3 如果假设1成立，则下面的不等式也成立：

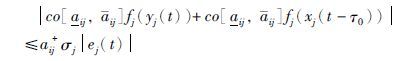
(11)

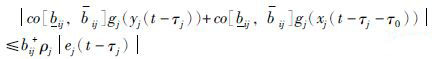
(26)

上式中，a_ij⁺=max｛a_ij^*，a_ij^**｝，b_ij⁺=max｛b_ij^*，b_ij^**｝.

证明 首先证明不等式(11a)，当y_i(t)=0和x_i(t-τ₀)=0时，显然式(11a)成立； 当y_i(t) ＜0且x_i(t-τ₀) ＜0时，|co[a_ij，a_ij]f_j(y_j(t))+co[a_ij，a_ij]f_j(x_j(t-τ₀))=co[a_ij，a_ij]f_j(y_j(t))+f_j(x_j(t-τ₀))|≤a_ij⁺σ_je_j(t)|； 当y_i(t) ＞0且x_i(t-τ₀)＞0时，co[a_ij，a_ij]f_j(y_j(t))+co[a_ij，a_ij]f_j(x_j(t-τ₀))≤a⁺_ijσ_je_j(t)，当x_i(t-τ₀) ,0 ＜y_i(t)或y_i(t)＜0＜x_i(t-τ₀)时，co[a_ij，a_ij]f_j(y_j(t))+co[a_ij，_ij]f_j(x_j(t-τ₀))≤co[[a_ij，a_ij]f_j(y_j(t))+f_j(x_j(t-τ₀))≤a⁺_ijσ_je_j(t).同理，采用类似分析，不等式(11b)也成立.

3 主要结果

定理1 若假设1成立，对于给定正数m_i，i=1，2，…，n, 总可以设计状态反馈控制器(5)，使控制器增益ω_ij，i, j=1，2，…，n, 满足以下不等式：

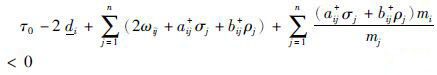
(12)

从而使驱动系统(1)与响应系统(3)实现延迟反同步.

证明 由式(12)得出，至少存在一个充分小的正数ε，使得以下不等式成立：

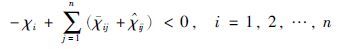
(13)

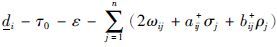
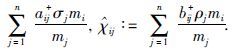
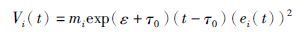
其中，χ_i∶=2，χ_ij∶=因此，选取李亚普诺夫函数为

(14)

对V_i(t)计算沿式(8)的右上Dini导数，可得

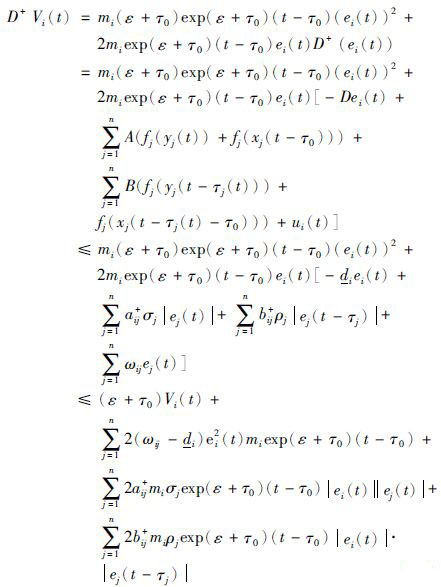
(15)

进一步地，由V_j(t)=m_jexp(ε+τ₀)(t-τ₀)(e_j(t))²，V_j(t-τ_j)=m_jexp(ε+τ₀)(t-τ₀)(e_j(t-τ_j))²，可以得到：

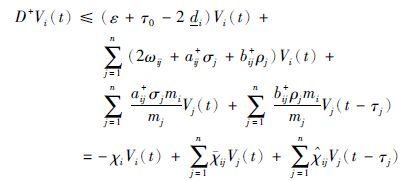
(16)

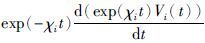
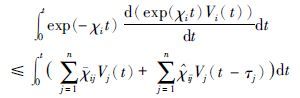
将展开D⁺V_i(t)+χ_iV_i(t)，对上式求积分，并由式(16)得

进而可以得出

进一步地，由上式可以得到：

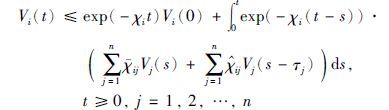
(17)

由于误差系统(8)的初始条件为e(s)=φ_τ0+ψ(s)=φ(s)，s∈[-τ，0]，i=1，2，…，n, 可以得到不等式：

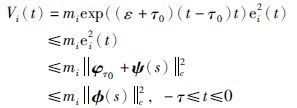
(18)

进一步地，利用引理1，由式(13)和式(18)可以得到：

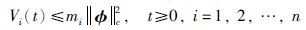
(19)

因此，

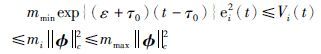
(20)

其中，.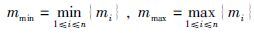

于是，由式(20)可以得到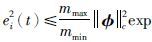(-(ε+τ₀)(t-τ₀)).

最后，可以得到e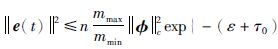(t-τ₀)｝，t≥0. 由定义1，得出延迟反同步误差e(t)可以收敛到0，并且得出延迟反同步率为ε+τ₀. 因此，定理证明完成.

推论1 若假设1成立，设计状态反馈控制器(5)，使控制器增益ω_ij，i, j=1，2，…，n, 满足以下不等式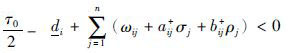：，那么驱动系统(1)与响应系统(3)实现延迟反同步.

证明 通过选取m_i=1，可以直接由定理1得到推论1. 推论1给出了一个简明的方案，驱动系统(1)与响应系统(3)可以实现延迟反同步.

定理2 在假设1成立的前提下，如果状态反馈控制器(5)增益Φ=(ω_ij)_n×n为负定的且满足下面的条件：

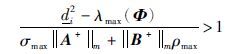
(21)

那么驱动系统(1)与响应系统(3)可以实现延迟反同步，其中，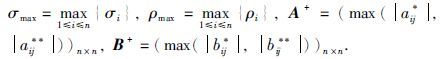

证明 构建一个李亚普诺夫函数为

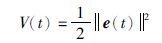
(22)

对V(t)计算沿式(8)的时间导数，可得

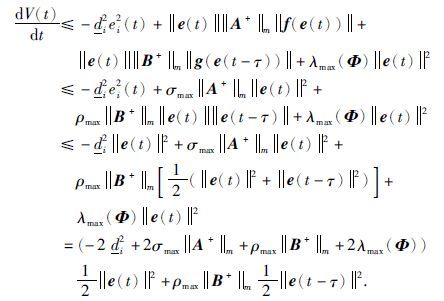
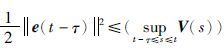
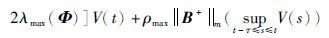
由于，因此，可以进一步地得出：

(23)

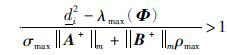
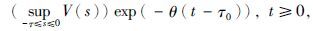
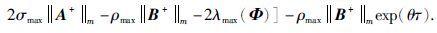
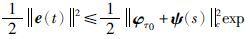
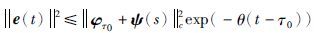
进一步地，将引理2应用到式(23)中，可以得出： 如果，那么2d_i²-2σ_max||A⁺||_m-ρ_max||B⁺||_m-2λ_max(Φ) ＞ρ_maxB_m⁺. 于是可以得到V(t)≤其中θ=2d_i²-因此，可以得出>(-θ(t-τ₀))，即，t≥0. 根据定义1，得出延迟反同步误差e(t)可以收敛到零，并且得出延迟反同步率为θ，证明完成.

注1 文^[14]研究了一般混沌系统的延迟反同步，然而忆阻器神经网络也是一类系统. 到目前为止，对于时滞混沌忆阻器神经网络延迟反同步控制的问题研究很少. 因此，在本文中，对时滞混沌忆阻器神经网络延迟反同步控制问题的研究补充和扩展了早期的研究成果.

注2 本文的定理1与文^[12]中的定理2相似，但文^[12]中的定理仅适用于忆阻器神经网络的反同步控制，而本文中的定理不仅适用于忆阻器神经网络的反同步控制(τ₀=0)，也同样适用于忆阻器神经网络的延迟反同步控制(τ₀ ＞0).

注3 为了研究忆阻器神经网络的动态特性，在文^{[12, 23-24]}中作了下面的假设：

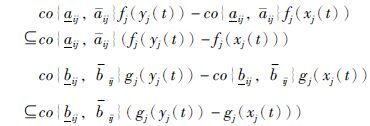
(24)

该假设条件只能在部分情况下满足，而引理3更容易满足，而且容易验证，本文使用引理3，减少了假设条件，因此本文减小了保守性.

4 数值例子

本节将证明所提的定理的有效性.

例1 考虑下面的2维忆阻器神经网络系统：

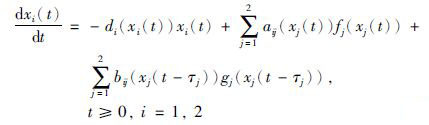
(25)

其中，

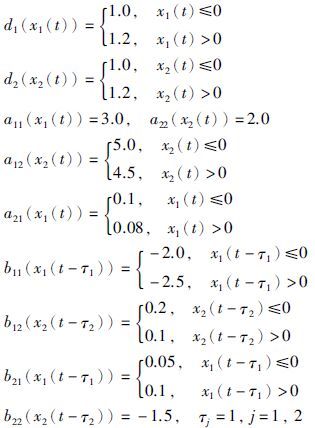
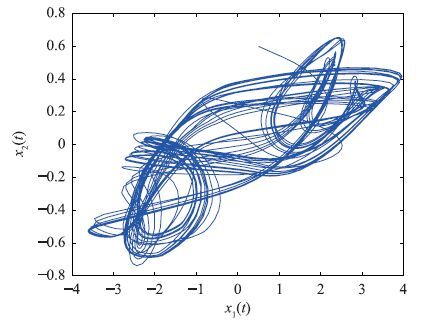
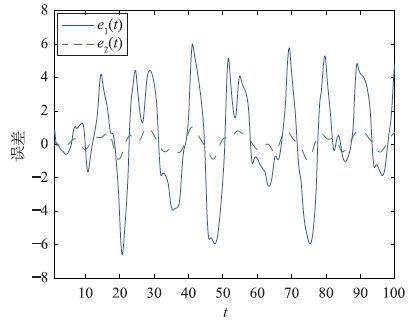
选取激活函数为f_j(x_j)=g_j(x_j)=tanh(x_j)，j=1，2. 将系统(25)作为驱动系统，其初始条件为x₁(s)=0.5，x₂(s)=0.6，∀s∈[-1，0)，其相图如图 1所示. 选取τ₀=1，在没有引入控制器的前提下，图 2分别给出了误差e₁(t)与e₂(t)随时间变化的曲线. 图 2中显示同步误差没有趋于0，表明驱动系统(25)与响应系统(3)没有达到延迟反同步.

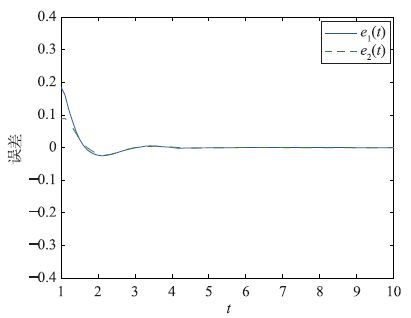
由式(7)可以得到d₁=1，d₂=1. 由式(11)可以得到a₁₁⁺=3，a₁₂⁺=5，a₂₁⁺=0.1，a₂₂⁺=2.0，b₁₁⁺=2.5，b₁₂⁺=0.2，b₂₁⁺=0.1，b₂₂⁺=1.5. 选取σ₁=ρ₁=1，σ₂=ρ₂=0，m_i=1，控制器增益ω₁₁=-8，ω₁₂=2，ω₂₁=2，ω₂₂=-8. 将上面的参数代入定理1中的条件，不等式(12)成立. 在引入了状态反馈控制器(5)的同时，图 3分别给出了同步误差e₁(t)与e₂(t)随时间变化的曲线. 由图 3可以看出同步误差趋于0，驱动系统(25)与响应系统(3)实现了延迟反同步.

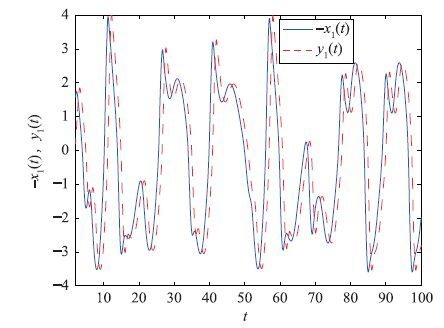
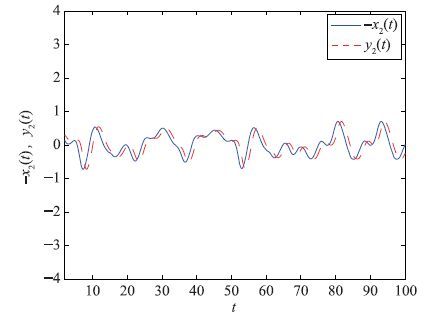
相应地，当τ₀=1时，图 4和图 5给出了反向驱动系统与响应系统(3)的状态响应曲线，即驱动系统(25)与响应系统(3)实现了延迟反同步.

5 结语

本文研究了基于时滞混沌忆阻器神经网络的延迟反同步控制问题. 在文［11-14,21-25]的基础上，首先基于非光滑分析和控制理论，并采用李亚普诺夫函数和Halanay不等式的方法，对充分性判据作了推广，使得定理应用范围更加广泛，并且减少了假设条件，从而延伸并改善了前人的工作. 最后，仿真结果验证了所提定理的有效性. 在此基础上，忆阻器神经网络在分布时滞或者混合时滞下的延迟反同步控制问题也是值得深入研究的.