1 引言
支持向量机理论[1]通过结构风险最小化原则提高学习机的泛化能力. 它在解决小样本、 非线性及模式识别问题中表现出许多优势,可推广应用到函数拟合研究中. 但是,其参数的设置对SVR(support vector regression)方法的学习性能及泛化性能具有较大影响. 如何减少参数设置对回归影响成为对支持向量机研究的一个热点. 同时,如何加快支持向量机训练速度也成为针对该算法研究的一个主要的方向.
传统方法所确定的支持向量回归参数,并不完全适合待回归区域,在运算过程中无法随数据分布而改变. 当数据分布复杂时,一组特定参数可能无法满足要求,导致回归曲线并不理想,不能达到要求的精度. 因此,如何根据数据分布实时设定参数成为解决问题的关键. 相关研究提出了一系列能够根据数据分布自动地调节参数设置的支持向量回归算法. 一方面获得比传统的固定参数方法更佳的回归性能,另一方面简化了参数的设置. 例如,Hao等人提出的Par-V-SVR(V-support vector machine with parametric in-sensitive/margin model)方法[2],使原本固定的参数ε随样本变化,使其更好地适应了数据样本的分布. 但是,核函数与正则参数依据需要人为设定. 在Hao工作基础上,Chen等人提出一种柔性支持向量机[3]算法,采用广义的损失函数和敏感损失函数实现参数函数化自动调节,但其算法计算量巨大不适于在线应用. 易辉等人提出另一种柔性支持向量同归法F-SVR(flexible support vector regression)[4]. 该算法实现了针对不同区间调整不同区域的参数,但由于不同区域间存在相互干扰现象,依靠经验选取参数方法[5]并不适用,使该算法在参数选择上更加困难、 不易收敛. 本文结合分段回归思想与区间复杂度划分的方法改善了参数设置对支持向量机回归效果的影响.
对于如何加快求解问题,相关研究提出许多方法,文[6-7]通过对二次规划机理研究提出smo算法和svmlight算法. 文[8-9]中根据支持向量机分类的几何性质,通过直接求取支持向量达到快速求解的目地. 文[10-11]通过聚类思想得到部分支持向量,加快了求解速度,但却使分类精度有所下降. 文[12]提出了根据样本类中心压缩数据的算法,取得了较好的分类效果. 一些数据在回归过程中并非必要,删除这些数据不仅不会影响回归,还能加快求解二次规划问题. 本文根据回归问题中数据在超球体内的分布特性,和欧氏距离与样本中心点距离,有选择地删除一些无用数据,即针对回归问题的向量预选取. 结合向量预选取及分段回归的方式,提出一种向量预选取的分段支持向量机回归算法.
2 支持向量机分段回归在传统支持向量机回归中,输入样本x首先通过非线性映射φ(x)映射到一个高维的特征空间,然后在这个特征空间中建立一个线性模型来估计回归函数,模型公式如下:
|
(1) |
其中,w为权向量; b为阈值. 对于给定的训练数据集(x1,y1),(x2,y2),(x3,y3)…(xn,yn),如果采用ε不敏感损失函数,则对应的支持向量机称为ε-支持向量机,其约束优化问题可表示为
|
(2) |
应用支持向量机对整个区间回归,关键是找到一组合适的参数满足下式:
|
(3) |
式(3)中左侧式子表示经验风险,右侧式子为置信范围,它们的和就是结构风险.
传统支持向量机参数设置直接影响了回归精度,针对不同的区域设置不同的参数可以减少参数设置对回归的影响.
对式(3)中左侧式子进行展开,由支持向量回归[13]定义可知,一个区间所划分的不同区域属于独立同分布的概率分布,则有如下等式成立:

|
(4) |
式(4)中f(x, w, γ)为预测函数集,R(w, γ)为支持向量回归的经验风险函数,l(y, f(x, w, γ)为损失函数,p(x, y)为概率分布.
假设把区间分为两个区域,两个区域的权向量分别为w1和w2
|
(5) |
式(5)下标为j时同理.
式(5)可以改写成为如下形式:
w为整个区间的权向量
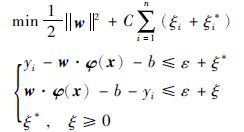
|
(6) |
通过解对偶问题得到式(5)的解:
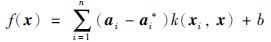
|
(7) |
式中,ai和ai*为拉格朗日乘子,它们只有一小部分不为0,它们对应的样本就是支持向量; k(x, xi)为核函数. 通常采用径向基核函数:
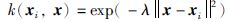
|
(8) |
其中λ为核参数.
3 区间划分式(9)为区间复杂度评估函数[4]. 给定区间样本(xi,yi),下式可用于评估分的复杂度:
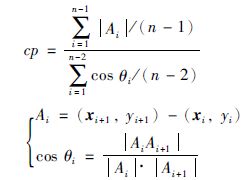
|
(9) |
文[4]中提出的复杂度一定程度上显示了曲线的复杂程度,cp值越大则数据越复杂,拥有相同密度却有不同变化趋势的样本,变化趋势大则表示图形复杂. 具有相同的变化趋势,而数据的密度不同,则密度大的复杂度小.
相邻不同区间cp绝对值的值差值越大则表明两区间复杂度差异越大.
定义1 子区间的复杂度与整个区间复杂度的比值为该区间的曲线特征. 曲线特征表达式即:
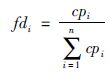
|
(10) |
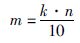
|
(11) |
式(10)中k为区间分段数,n为训练样本数.
对于不同的k值,在待分区间内对样本进行m次随机划分. 分别测试k=1,2,3,4,5时h的值,h的值取最大值时所对应的k值作为最终区间划分值. h的计算方法如式(12)所示:
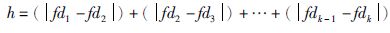
|
(12) |
在应用支持向量机线回归建模时,庞大的数据会使求解二次规划问题变得很困难,减少不必要的样本数据数量,可以大大减少算法运行时间. 如何合理地减少数据成为解决这一问题的关键. 拉格朗日乘子不为零,即为支持向量,只有这些乘子所对应的数据才对回归有作用.
如图 1所示支持向量回归可以看成一种特殊的二分类问题,我们无需指定正负类样本,算法根据参数自动划分,回归曲线在这两类样本所对应的支持向量间. D3、 D4所在空间为支持向量所在区域,只有这部分区域内才是有效信息. 针对支持向量回归中这类几何特性可知,D2之间区域范围必定为无用信息.
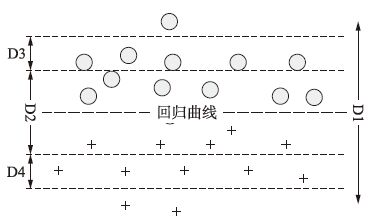
|
| 图 1 回归曲线示意图 Figure 1 Schematic diagram of regression curve |
由此出发点考虑,除去这些无用的数据,势必会加快支持向量机回归的速度. 这时出现一个如何确定D2范围的问题.
高维空间内,样本中心坐标计算公式如下:
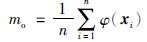
|
(13) |
虽然我们不知道φ(x)的具体表达式,但可用下式计算x到达样本中心的距离[14]:
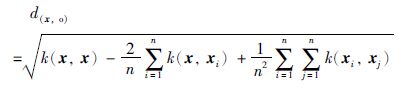
|
(14) |
步骤1 如图 2所示,将数据映射到高维空间,根据式(14)可以计算任意x到样本中心点的距离,这样就可以找到样本与样本中心欧氏距离最大的一点,距离记为a,然后计算其它点到样本中心的欧氏距离的平均值,距离记作b, 距样本中心最近一点距离记作c; a、 b、 c将整个超球体空间分为两个区域,分别定义为外环和内环. 内环区域就是数据约简区间. 由于将空间距离转化为平面距离,它不足以表征空间分布所有特性,所以数据约减前,要通过一部分数据验证支持向量的大概分布范围,当支持向量分布比较均匀时,本文提出的方法会导致回归精度下降.
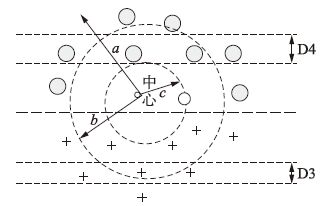
|
| 图 2 数据分布示意图 Figure 2 Schematic diagram of data distribution |
在约简范围内不仅有非支持向量还有支持向量和近似支持向量[15],近似支持向量是有可能成为支持向量的数据. 当参数设置比较恰当时,这些数据并不起作用,相反则这些向量起到作用. b到c范围内包含了这三类向量. 删除支持向量的同时删除近似支持向量,这种不当的删除数据会导致回归信息失真.
步骤2 计算约简区间内数据个数CB,计算其占总数据的百分比CA,一般情况下支持向量占总数30%~50%,此时可计算大约支持向量数量: M=0.4×CB. 某些情况下待约简区域需进行一定的调整. 如果CA小于30%,则要通过σ1进行修正,使待删区域RD整体向样本中心收缩. 有时待删数据是连续的,较大程度上损失了回归信息,这时就要对此待删区间w进行调整. 调整公式为
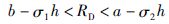
|
(15) |
其中h=a-b,同时需要对此待删区间进行随机取值,目的是减少对支持向量和拟支持向量数据的误删除.
步骤3 式(15)中的参数σ1、 σ2为(0,1)之间的缩放因子,其取值对于待删区域选择的影响很大. 一般取σ1=σ2,设定σ的初值0.1~0.15,通过调整步长(设为0.05),使σ逐渐扩大,从而使待删区域进行移动,避开数据相关性较大区域,最终找到一个合适的区域. 把连续数据和其占被删数据的百分比(大约为5%~10%)作为评判待删区域w是否合适的标准之一. 另一个标准为平方相关系r, 它的值要大于0.8.
向量预选取的分段支持向量机回归算法流程如图 3所示.
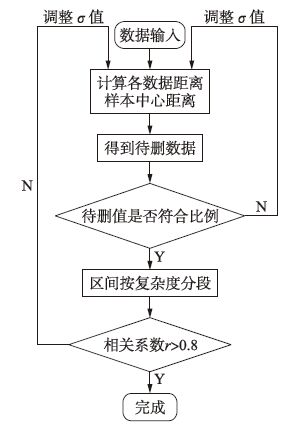
|
| 图 3 向量预选取的分段支持向量机回归算法流程 Figure 3 The process of vector pre-selected piecewise regression algorithm of support vector machines |
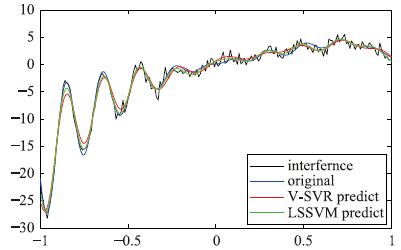
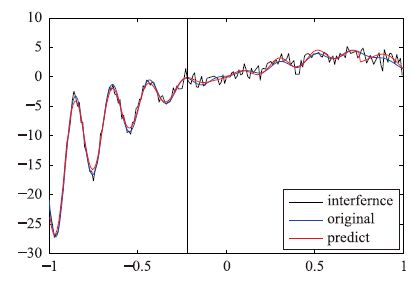
图 4和图 5的测试函数取自文[4],取400样本,区间[-1, 1],并加入随机干扰信号,信噪比19,其中200个样本进行训练,200个样本进行测试. 图 7数据取自UCI数据库[16]. 该数据因变量为中位数(MEDV),自变量有13个分别为: CRIM,ZN,INDUS,CHAS,NOX,RM,AGE,DIS,RAD,TAX,PTRATIO,B,LSTAT. CRIM分布范围广,但大多集中在0附近,存在偏态,做如下变换CRIM=ln(CRIM).
|
| 图 4 对比回归测试 Figure 4 Contrast regression testing |
|
| 图 5 p-p-SVR回归测试 Figure 5 p-p-SVR regression testing |
|
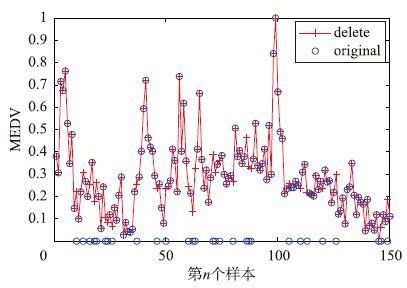
| 图 6 删除点位置 Figure 6 Deleted point position |

|
| 图 7 对比回归测试 Figure 7 Contrast regression testing |
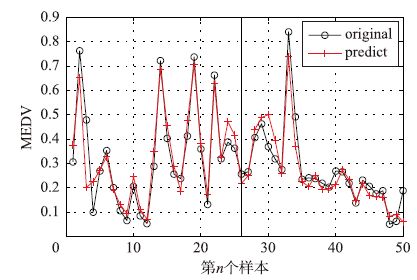
原数据共506个,取前150个数据进行测试. 图 7为未删除数据时用传统SVR进行回归得到的回归曲线. 图 8为删除数据位置后,得到的测试数据回归曲线.
| 算法 | V-SVR | LSSVM | p-p-SVR |
| 训练时间 | 0.06 | 0.05 | 0.502 9 |
| 算法 | 支持向量数 | 删除数据数 | 样本数 | σ值 |
| V-SVR | 71 | 0 | 200 | |
| LSSVM | 200 | 0 | 200 | |
| p-p-SVR | 34 | 33 | 200 | σ=1/5 |
在输入为单维的情况下,由图 4和图 5对比可看到,利用V-SVR(V-support vector machine)和LSSVM(least square support vector regression)得到的回归结果是前半部分欠拟合,而后半部分过拟合. p-p-SVR两部分回归的精度有所提高,删除的数据并没有使回归精度降低. 由表 1三种算法计算时间比较可以看出,减少支持向量数量,并没有使回归更加迅速. 这是由于本例中输入量维度较少,使向量预选取的优点不能体现.
在输入为多维的情况下,由图 6和图 8可以看出本文提出的预选向量算法在不影响回归精度的前提下,依然可以有效地对数据进行删除. 图 7与图 8对比体现了分段回归的方法使回归精度相对于V-SVR和LSSVM有所提高. 由表 3可以看出本文算法训练时间少于V-SVR,证明了本文所提预选向量算法的有效性. 表 3与表 1的对比体现了在输入量维度较大时,本文所提出的向量预选取可以减少运算的优势.
|
| 图 8 p-p-SVR测试回归 Figure 8 p-p-SVR test regression |
| 算法 | V-SVR | LSSVM | p-p-SVR |
| 训练时间 | 0.04 | 0.008 | 0.013 |
| 算法 | 支持向量数 | 删除数据数 | 样本数 | σ值 |
| V-SVR | 52 | 0 | 100 | |
| LSSVM | 100 | 0 | 100 | |
| p-p-SVR | 41 | 28 | 100 | σ=1/8 |
本文通过对支持向量回归空间特性的分析提出了预选向量方法,根据不同复杂度区间提出了分段回归的方法. 向量预选取分段支持向量机回归算法在一定程度上减少训练样本的个数,针对输入为高维度的训练样本的回归问题,提高了训练速度的同时,使回归精度有所提高. 它有效地克服了F-SVR参数选择和传统SVR在某一区间回归精度差的问题. 如何更加快速准确地确定收缩因子σ的值是下一步主要研究的问题.
| [1] | Vapnik V N. The nature of statistical learning theory[J]. Berlin, Germany: Springer-Verlag , 1995 . |
| [2] | Hao P Y. New support vector algorithms with parametric in-sensitive/margin model[J]. Neural Networks , 2010, 23 (1) : 60–73. DOI:10.1016/j.neunet.2009.08.001 |
| [3] | Xiao B C, Jian Y, Jun L. A flexible support vector machine for regression neural[J]. Neural Computing & Applications , 2012, 21 (8) : 2005–2013. DOI:10.1007/s00521-011-0623-5 |
| [4] | 易辉, 宋晓峰, 姜斌, 等. 柔性支持向量回归及其在故障检测中的应用[J]. 自动化学报 , 2013, 39 (3) : 272–284. Yi H, Song X F, Jiang B, et al. A flexible support vector regression and its application in fault detection[J]. Automation Journal , 2013, 39 (3) : 272–284. |
| [5] | Vladimir C, Yun Q M. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks , 2004, 17 (1) : 113–126. DOI:10.1016/S0893-6080(03)00169-2 |
| [6] | Platt J C. Sequential minimal optimization - A fast algorithm for training support vector machines[M]. Berlin, Germany: Springer , 1998 . |
| [7] | Joachims T. Making large-scale support vector machine learning practical[M]. Cambridge, MA, USA: MIT Press , 1999 . |
| [8] | 李庆, 胡捍英. 支持向量预选取的K边界近邻法[J]. 新能源进展 , 2013, 18 (2) : 91–96. Li Q, Hu H Y. The K boundary nearest neighbor of support vector pre-selection[J]. New Energy Progress , 2013, 18 (2) : 91–96. |
| [9] | 杨静, 于旭, 谢志强, 等. 改进向量投影的支持向量预选取方法[J]. 计算机学报 , 2012, 35 (5) : 1002–1010. Yang J, Yu X, Xie Z Q, et al. A support vector selection method for improving vector projection[J]. Computer Journal , 2012, 35 (5) : 1002–1010. |
| [10] | Shi J H, Su M Y, Chen Y S. A novel intrusion detection system based on hierarchical clustering and support vector machines[J]. Expert Systems with Application , 2011, 38 (1) : 175–181. DOI:10.1016/j.eswa.2010.06.036 |
| [11] | Dong X N, Wei Y N. An improved short-term power load combined forecasting with ARMA-GRACH-ANN-SVM based on FHNN similar-day clustering[J]. Journal of Software , 2013, 8 (3) : 341–346. |
| [12] | 庞首颜, 陈松, 魏建猛, 等. 基于类中心的SVM训练样本集缩减改进策略[J]. 重庆交通大学学报: 自然科学版 , 2014, 33 (2) : 154–158. Pang S Y, Chen S, Wei J M, et al. SVM training sample set reduction strategy based on class center[J]. Journal of Chongqing Jiaotong University: Natural Science Edition , 2014, 33 (2) : 154–158. |
| [13] | 胡良谋, 曹克强, 徐浩军, 等. 支持向量机故障诊断及控制技术[M]. 北京: 国防工业出版社 ,2011 . Hu L M, Cao K Q, Xu H J, et al. A support vector machine fault diagnosis and control technology[M]. Beijing: Defense Industry Press , 2011 . |
| [14] | 焦李成, 张莉, 周伟达, 等. 支撑矢量预选取的中心距离比值法[J]. 电子学报 , 2001, 29 (3) : 383–386. Jiao L C, Zhang L, Zhou W D, et al. A center distance ratio of support vector pre selection[J]. Electronic Journal , 2001, 29 (3) : 383–386. |
| [15] | 蒋刚, 肖建. 一种支持向量预提取方法及应用[J]. 广西师范大学学报: 自然科学版 , 2006, 24 (4) : 123–126. Jiang G, Xiao J. A support vector extraction method and application[J]. Journal of Guangxi Normal University: Natural Science Edition , 2006, 24 (4) : 123–126. |
| [16] | Harrison D, Rubinfeld, D L. Hedonic prices and the demand for clean air[J]. Journal of Environmental Economics & Management , 1978, 43 (6) : 81–102. |



