1 引言
公司和终端用户越来越依赖于云服务商提供的服务,如软件即服务(SaaS)、 云平台即服务(PaaS)和基础设施即服务(IaaS)等[1-2]. 然而,客户和云服务商间能否遵守服务水平协议(SLA)则主要取决于硬件资源的可用性. 例如,在北美洲,云数据中心突发故障的平均代价是每分钟5 000美元[3]. 虚拟化技术[4]在云计算中扮演着重要角色,它可使许多其他服务在同一硬件资源中共存. 此时,如果发生硬件故障将导致多个客户的资源失能,给云服务器造成严重损失. 本文重点研究基础设施即服务(IaaS),更准确的说,重点研究云骨干技术中的网络即服务(NaaS). 云服务商(CP)依托其主干向客户租赁虚拟网络资源. 在NaaS服务中,每个客户将请求由其拓扑结构定义的虚拟网络(VN)以及虚拟路由器和使用链路的容量(比如处理能力,内存和带宽等).
虚拟网络嵌入问题已经被广泛的研究,文[5]提出一种生存型虚拟网络嵌入算法(SVNE)来处理底层链路故障. SVNE包括3个独立步骤: 首先,CP在没有到达任何VN请求之前,利用链路选择算法为每条底层链路计算一组潜在备份迂回路径. 然后,当VN请求到达时利用D-VINE(based on the topological structure of the virtual network embedded algorithm)算法[6]来嵌入VN请求. 最后,如果有一条底层链路发生故障,则进行被动式备份迂回路径优化. 然而该文假设底层节点可永久运行,这显然不切实际. 文[7]提出一种融合了VN映射和底层链路备份的远程访问算法RMap(Combines VN mapping and the underlying link backup remote access algorithm). 然而,RMap只保证了受压链路得到保护,非受压链路则没有得到保护. 因此,如果非受压链路发生故障,则涉及该底层链路的所有虚拟网络都将受到影响. 文[8]提出基于人工蜂群元启发式算法的预防性VN嵌入策略PR-VNE(heuristic algorithm based on artificial colony yuan preventive. vn embedding strategy). 然而,PR-VNE没有采取任何补救性机制来应对硬件故障. 一旦发生物理故障,受到影响的所有VN将从底层网络(SN)中消失,违反了签署过的服务水平协议,迫使CP付出代价,降低了云计算性能. 为此,本文提出一种面向虚拟网络嵌入的协作博弈(CG-VNE)方法,以提升云供应商的收入和处理物理故障的能力. 其目的是: (1) 对SN中的物理资源进行公平管理; (2) 接受更多新客户,使供应商的收入最大化; (3) 将受到物理故障影响的客户数量降到最低; (4) 对受到影响的VN重新映射.
VN嵌入问题是个多目标非线性优化问题,该问题是NP难题[9]. 为了避免指数级复杂性,根据相同利益博弈(IIG)理论[10],CG-VNE方法将VN嵌入问题阐述为两个互相嵌套的IIG博弈. 第1个博弈处理虚拟节点映射问题,第2个博弈处理虚拟链路的嵌入问题. 在前一种博弈中,认为每个虚拟路由器是一个虚拟博弈方,其特征可用它的初始嵌入底层节点和一组行为(即策略)来描述. 本文将行为集定义为虚拟路由器可移动的一组物理路由器(比如单跳相邻路由器等). 为了估计虚拟路由器博弈方的行为收益,提出进行第2次IIG博弈,以便对其连接的虚拟链路进行映射. 虚拟链路博弈由虚拟博弈方构成. 每个博弈方可从虚拟链路和托管着与上述虚拟链路相连的虚拟路由器的底层路由器两个方面进行描述. 与虚拟路由器博弈类似,每个虚拟链路博弈方可用一组行为进行描述,每次利用收益函数进行优选. 本文IIG博弈属于势力场博弈,存在纳什平衡. 为了达到这种平衡,CG-VNE采用了文[11]中的最优响应算法,以保证可收敛到纳什平衡. 通过全面的仿真实验,评估了CG-VNE相对其他虚拟网络嵌入算法的性能. 实验结果表明,在新VN拒绝率、 云服务收入及受到故障影响的VN率3个方面,CG-VNE的性能更优.
2 问题描述本节给出可靠性VN嵌入问题的定义. 首先描述如下模型: (1) 网络模型(即底层网络和虚拟网络); (2) 物理设备(即路由器和链路)故障. 然后,详细给出基于博弈论的问题定义,以及博弈方、 收益和效用函数的确切定义.
2.1 网络和物理故障模型为了描述方便,用D表示VN,用G表示SN. 本文从可靠性、 带宽、 处理性能和内存4个角度来描述每个底层设备(即路由器和链路). 假设,G中的资源是有限的,G无法托管无限多个VN请求. 物理设备可靠性与其年龄成反比. 即物理设备使用时间越长,发生故障的概率越大. 因此,只有对G实现VN嵌入,才能尽量提高VN请求的接受率以及受到物理故障影响的VN恢复率. 因此,通过接受更多客户,降低由于故障导致的惩罚代价,CP可实现其收益最大.
将SN描述为一种无向图G=(V(G),E(G)),其中V(G)和E(G)分别表示物理路由器集合及其所连的链路集合. 每个物理路由器w∈V(G)从以下方面描述: (1) 剩余处理性能B(w); (2) 剩余内存M(w); (3) 类型: 接入型还是核心型X(w); (4) 在时间t时的可靠性Rn(w, t). 请注意,如果X(w)=1,则w是一种接入路由器(access router). 否则,X(w)=0. 类似地,每条物理链路e∈E(G)可从如下方面描述: (1) 剩余带宽C(e); (2) 容量带宽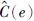
本文将故障间的平均时间(mean time between failures, MTBF)建模为Weibull分布[12]. 相应地,可以估计设备在任何时刻的可靠性. MTBF的累积分布函数(CDF)定义如下:
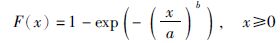
|
(1) |
其中,a和b是Weibull分布的参数. 本文假设物理网络的年龄不同. 即G中的任意设备均有其自己的初始年龄,比如底层节点w和底层链路e的初始年龄分别为A(w)和A(e). 因此,SN中的设备分为3组: (1) 年轻组; (2) 成年组; (3) 老化组. 请注意,Rn(w, t)=F(A(w)+t),且Rl(e, t)=F(A(e)+t),其中t是当前仿真时间.
同时,将VN请求表述为一种无向图D=(V(D),E(D)),其中V(D)和E(D)分别表示虚拟路由器集合及其虚拟链路集合. 每个虚拟路由器v∈V(D)可从如下方面描述: (1) 要求的处理性能B(v); (2) 内存M(v); (3) 类型X(v). 此外,每条虚拟链路d∈E(D)可用其带宽要求C(d)来描述.
2.2 基于博弈论的问题描述本文重点讨论底层图G中虚拟图D的映射,同时考虑G的可靠性以及虚拟网络嵌入约束[13],比如(1) 边缘/核路由器; (2) 链路/路由器的剩余容量; (3) 不可分的底层路径,等等. 本文目的如下: (1) 使VN请求的拒绝率最小; (2) 使受到物理故障影响的嵌入式VN的数量最小; (3) 物理故障出现后迅速处理故障. 为此,将可靠性VN嵌入问题表述为一种博弈问题. 一次博弈Γ(N,S,U)可用3个参数描述:
(1) N={N1,…,Np}: 博弈方集合,其中: p为常量.
(2) S是所有博弈方N的行为描述. 它等价于S=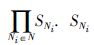
(3) U是博弈问题效用函数向量. U等价于(UN1,…,UNp). UN1表示博弈方Ni的效用函数,且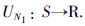
受到相同利益博弈(IIG)理论的启发,本文将可靠性VN嵌入问题表述为两个互相嵌套(交错)的博弈. 第1个博弈Γ1处理虚拟路由器. 在虚拟路由器博弈的每一轮期间,进行第2种博弈Γ2来处理虚拟链路的嵌入. 下文将定义两种博弈的参数.
在第1种博弈Γ1(N1,S1,U1)中,定义一组与虚拟路由器V(D)相对应的虚拟博弈方N1. 假设每个虚拟路由器博弈方在底层图G中均有一个初始映射. 每个虚拟博弈方N1i的行动集S1Ni1由托管着博弈方Ni1的当前底层路由器的K跳相邻路由器和从V(G)中随机选择的一组底层路由器构成. 所有底层路由器sN1i∈S1N1i具有如下特征: (1) 具有足够多的资源(即B(Ni1)≤B(sN1i),M(Ni1)≤M(sN1i)),因此有能力托管博弈方; (2) 具有相同的类型(即X(Ni1)=X(sN1i)). 每个博弈方Ni1的收益函数U1N1i取决于: (1) 托管着博弈方的底层节点wN1i的剩余资源(即内存和处理能力); (2) 它的可靠性; (3) 与其相连的虚拟链路获得的收益. 正式地,
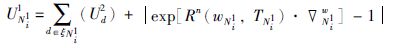
|
(2) |
其中,Ud2表示虚拟链路d的收益函数; ξN1i表示与虚拟路由器博弈方Ni1相连的虚拟链路集合; Rn(wN1i,TN1i)表示在时间TN1i托管着虚拟路由器博弈方的底层路由器w的可靠性. 请注意,TN1i对应于虚拟网络D的离开时间,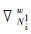
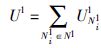
|
(3) |
第2种博弈Γ2(N2,S2,U2)处理基于社交的虚拟链路嵌入问题. 定义一组新的虚拟博弈方N2,每个博弈方Ni2对应于一条虚拟链路d∈E(D)和托管着虚拟路由器末端的两个底层路由器. 博弈方通过使用相同的效用函数来间接地展开合作. 每个虚拟链路博弈方Ni2可由其行动集S2N2i描述. 后者由一组底层路径构成,这些底层路径将托管着虚拟路由器末端的两个物理路由器连接起来. 每条路径sN2i∈S2N2i可托管虚拟链路博弈方Ni2(即C(Ni2)≤C(sN2i)). 虚拟链路博弈方Ni2采取行动sN2i∈S2N2i(即底层路径)时的效用函数U2N2i取决于: (1) sN2i的剩余带宽; (2) sN2i提供的可靠性.
于是,有:
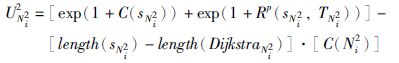
|
(4) |
其中: (1) Rp(sN2i,TN2i)表示虚拟网络D离开物理骨干网G时底层路径sN2i在TN2i时刻的可靠性; (2) length(sN2i)对应于sN2i的跳数; (3) DijkstraN2i表示托管着虚拟链路博弈方Ni2的最短路径. 底层路径sN2i的容量等于其底层链路的最小剩余带宽. 此外,底层路径sN2i的可靠性Rp(sN2i,TN2i)等于其所有底层链路和节点的可靠性乘积. 效用函数为
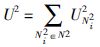
|
(5) |
于是,可知U1N1i和U2N2i的收益函数使VN的可靠性最大. 实际上,后面的函数与所选择的底层资源的可靠性成正比. 此外,两个收益函数包括了剩余资源的数量,因此考虑了新的VN请求的接受率. 类似地,U1N1i和U2N2i与SN中的剩余资源成正比. 通过这种方法,可以避免底层资源的拥塞,并实现其使用率的负载均衡最大化.
各种博弈策略的主要目的均是实现纳什均衡(NE). NE是指这样一组行为,每个博弈方Ni采取一种行为后,没有博弈方会单方面地更改其行为. 换句话说,如果假设其他博弈方的策略保持不变,则NE所表示的稳态下,各方单方面背离其选择并不会提升其收益. 正式地,如果对∀Ni∈N,∀sNi∈SNi,有UNi(s*Ni,S*-Ni)≥UNi(sNi,S*-Ni)且S*-Ni=S*\s*Ni,则策略S*=(s*N1,…,s*Np)为NE均衡.
然而,NE均衡并不一定存在. 下文将证明本文模型包括至少一种NE均衡. 如上文所示,本文的可靠性VN嵌入被阐述为一种相同利益博弈(IIG). IIG是势力场博弈的特殊情况[14],可定义势函数等价于所有博弈方共享的共同效用函数. 于是,可利用满足如下条件的势函数f来描述势力场博弈:
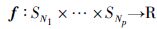
|
(6) |
其中∀Ni∈N,∀sNi1,s2Ni∈SNi∶f(sNi1,S1-Ni)-f(s2Ni,S2-Ni)=UNi(sNi1,s1-Ni)-UNi(s2Ni,s2-Ni). 势力场博弈具有如下两种属性: (1) 每个有限(即行为基数|S|有限)势力场博弈至少有一种纯策略达到纳什平衡. (2) 所有纳什平衡要么使效用函数U局部最大,要么使其全局最大. 因此,可认为本文高可靠性VN问题存在NE平衡. 下节将详细讨论可实现博弈Γ1(N1,S1,U1)和Γ2(N2,S2,U2)达到纳什平衡的算法CG-VNE.
3 CG-VNE算法第2小节将高可靠性VN问题描述为两种交替博弈Γ1和Γ2. 为了实现NE平衡,每个博弈方Ni每次从其行为集SNi中选择最优行为来运行最优响应算法(BR)[11]. 为了到达NE稳态,根据BR算法运行算法1. 该算法的步骤如下. 首先,对每个博弈方Ni,它可确定其行为集SNi. 然后,确定每个博弈方Ni的次序. 于是,每个博弈方Ni在轮到自己的次序时,从SNi中选择可使其收益函数UNi最大的最优行为(即运行BR算法). 一旦所有博弈方N={Ni}操作结束,则评估效用函数U. 如果先前值和新值间的差值低于预定义的阈值εΓ,则认为到达NE平衡. 否则,从决定次序的步骤开始重复上述过程.
| 算法1: NE计算 |
| 1: 输入: Γ(N,S,U) |
| 2: 输出: 表示NE的s*=(sN1*,…,s*Np),s*∈S |
| 3: 确定每个博弈方Ni∈N的行为集SNi |
| 4: 计算每个博弈方Ni的初始收益U0Ni |
5: 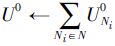
|
| 6: repeat |
| 7: {Nj}←TurnPlayers(N) |
| 8: for j←1 toN do |
| 9: s*Nj←{s*Nj∈SNj: UNj(s*Nj)=maxsNj∈SNj[UNj(sNj)]} |
| 10: U*Nj∈UNj(s*Nj) |
11: 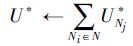 |
12:  |
| 13: U0←U* |
14: 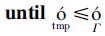
|
第1个博弈Γ1(N1,S1,U1)处理虚拟路由器的映射问题. 然而,虚拟路由器的收益U1N1i取决于与其相连的虚拟链路的收益(见式(2)). 为了映射虚拟链路,需要求解博弈Γ2(N2,S2,U2). 可以看出,从这个角度讲,两个博弈是互相交错的. 本文算法的伪代码见算法2.
| 算法2: CG-VNE |
| 1: 输入: G=(V(G),E(G)),D=(V(D),E(D)) |
| 2: 输出: G中D的映射 |
| 3: 确定D的初始嵌入 |
| 4: 构建Γ1的博弈方集合: N1←V(D) |
| 5: 确定每个博弈方Ni1∈N1的行为集S1N1i |
6: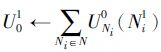 |
| 7: repeat |
| 8: {Nj1}←TurnPlayers(N1) |
| 9: for j←1 to |N| do |
| 10:for each N1j, k∈S1N1j do |
| 11:构建第2个博弈Γ2的博弈方集合: N2←与Nj1相连的虚拟链路 |
| 12:确定每个博弈方Nk2∈N2的行动集S2N2k |
| 13: NE(Γ2(N2,S2,U2))计算 |
| 14:选择可使收益函数UN1j1最大的最优候选Nj, k1*∈S1N1j(最大值等于U1best(Nj1)) |
15: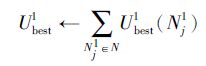 |
16: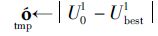 |
17: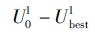 |
18: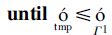 |
每个虚拟路由器博弈方SNi1的候选由托管虚拟博弈方Ni的初始底层路由器的H-邻域以及为了避免局部最优而随机选择的一部分底层候选构成. 通过这种方法,可以重点研究邻域和远程解. 将虚拟链路路径的候选连接起来后,可以首先在源节点和目的地间生成L条(L first)K-最短路径. 最后,在博弈Γ1和Γ2中,博弈方的次序(即TurnPlayers步骤)遵守离散均匀分布.
CG-VNE通过两个步骤处理可靠性问题. 第1步是预防性步骤,在候选S1和S2的选择期间执行. 实际上,两个交错博弈Γ1和Γ2的收益和效用函数,可促使选择可靠性较高(即故障概率较低)的资源. 相应地,本文方法通过避免非可靠性底层资源(即路由器和链路)来防止故障的发生. 第2步是一种被动策略. 当发生故障时,CG-VNE执行恢复流程. 实际上,本文算法是对受到影响的虚拟资源(即路由器和链路)进行重新嵌入. 利用同样的博弈Γ1和Γ2来嵌入受到影响的虚拟资源. 被动策略是受到了底层资源消耗优化的启发. 实际上,专门分配了可能未被使用的备份资源,以缓解网络压力. 为了保证恢复效果,本文根据文[15]设计了一种中央底层控制器,存储所有虚拟资源的检测点.
算法CG-VNE的时间复杂度主要取决于博弈Γ1(N1,S1,U1)和博弈Γ2(N2,S2,U2). 其中,在博弈Γ1(N1,S1,U1)中,它的主要时间开销在于从底层图G中的初始映射中确定博弈方N1i的行动集S1Ni1后进行虚拟节点映射,该问题的难度取决于G的规模,依据文[10]可知,它可在多项式时间内实现纳什均衡. 在博弈Γ2(N2,S2,U2)中,它的主要时间开销在于NE计算,而根据算法1可知,NE计算主要取决于效用函数U,每次利用效用函数U进行优选,是一种势力场博弈,依据文[14]可知,该博弈可在多项式时间内实现U最大化,即实现纳什均衡. 综上所述,算法CG-VNE的时间复杂度是可控的,能够满足终端用户对于云供应商所提供的服务的需求.
4 性能评估本节通过全面的仿真实验来评估CG-VNE算法的有效性. 首先描述考虑了SN可靠性和设备年龄的离散事件模拟器. 然后定义了性能指标,并将本文算法与其他主流生存型嵌入式虚拟网络策略如SVNE[5]、 RMap[7]和PR-VNE[8]进行了性能比较.
4.1 仿真环境
部署了一种离散事件高可靠性VN映射模拟器. 为此,采用文[16]中的GT-ITM(Georgia tech internetwork topology models)来生成随机SN和VN拓扑结构. 利用速率为IA的泊松过程来模拟VN请求的到达情况. 利用均值为mL的指数分布来模拟VN的寿命. 将SN的规模设置为100. 此时,接入路由器和核心路由器的比例分别固定为20%和80%. 此外,根据范围为[3, 10]的离散均匀分布来设置VN的规模. 接入型虚拟节点的比例相同,比如每个VN的SN为20%. 请注意,在两种情况下(SN和VN),每对路由器随机相连的概率为0.5. 到达率IA和VN的平均寿命mL分别设置为每100个单位时间4个请求及1 000个时间单位. 根据范围为[50, 100]的连续均匀分布来调整底层节点和链路的容量(即B(w),M(w),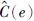
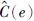
对于SN的可靠性,模拟MTBF的Weibull分布的参数a和b分别设置为25×104和1.5. 请注意,将a和b调整后,获得的每个物理设备的寿命(≈6×105)大约是仿真时间(≈6×104)的10倍. 此外,SN中年轻设备的比例设为30%. 本文研究相对于SN中成年部分(及老化部分)的性能. 因此,物理设备的初始年龄在其群组范围内(即年轻,成年和老化组)遵守均匀分布. 在本文模拟器中部署了CG-VNE及其他几种相关算法: PR-VNE算法、 生存型虚拟网络嵌入算法(SVNE)和RMap算法. 将VN请求数量设置为2 000. 将CG-VNE的参数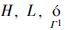
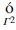
下面给出衡量CG-VNE的各个指标的定义.
(1) Q: 仿真期间VN请求的拒绝率. 即没有在SN中映射的VN的比率.
(2) F: 已经部署的VN中,在仿真期间受到物理故障影响的VN的比率. 实际上,对一个VN来说,如果它有至少一个组件(即虚拟路由器或链路)受到物理故障的影响,即认为该VN受到影响.
(3) G: 评估SN供应方的收益情况,计算方法是所有被接受的VN请求的总收益G1,减去整个仿真期间因物理故障导致的向客户支持的惩罚G2(G=G1-G2). G1的定义见文[6]. 它取决于被请求的资源量及主干网络SN中虚拟网络的寿命. 将惩罚G2定义为向客户支付的罚金. 代价与惩罚率为δ时VN的剩余时间成正比. 正式地,如果用D来表示各个VN,则有:
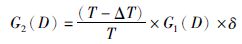
|
(7) |
其中ΔT表示物理故障发生前SN的托管持续时间,δ是惩罚率. 本文仿真将惩罚率设置为50%.
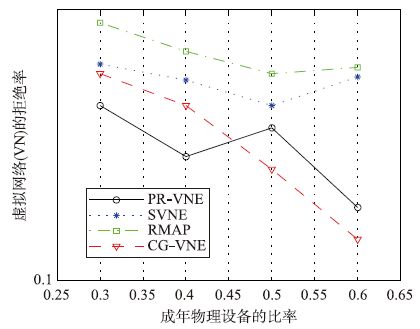
4.3 仿真结果图 1比较了CG-VNE和其他相关算法的VN请求拒绝率Q. 从图 1可以看到,当成年设备的比例大于45%或者老化设备不到25%时本文算法优于其他算法. 这一现象的原因在于故障恢复期间采用的资源分配策略. 实际上,如果它能够重新分配受到影响的虚拟资源,则即使出现物理故障,CG-VNE也可以在云主干中维护一个VN,而PR-VNE不是如此. 如果物理故障影响到了虚拟网络内一个或一个以上的设备,则分配给它的所有资源都将被释放. 换句话说,在物理故障期间,PR-VNE不会做出响应,为受到影响的VN分配的所有资源都将被释放. 另外可以注意到,虽然RMap和SVNE没有对故障做出响应,但是CG-VNE的拒绝率仍然低于RMap和SVNE.
|
| 图 1 拒绝率Q Figure 1 Rejection rate Q |
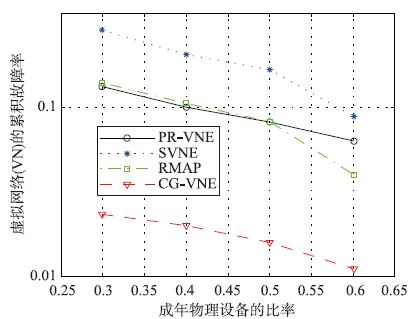
图 2评估了物理故障导致的未被修复的VN的影响率F. 可以明显看出,由于在映射期间采取了恢复机制和防护措施(见收益函数),CG-VNE的性能优于其他策略. 例如,当成年设备的比例等于30%,老化设备为40%时,CG-VNE将故障导致的VN崩溃率下降了85%左右. 被影响的VN的下降幅度相对于成年设备来说更为明显. 主要原因是SN的故障下降. 实际上,当成年设备数量上升时,SN更为年轻.
|
| 图 2 受到故障影响的VN的比率F Figure 2 The ratio of VN affected by fault F |
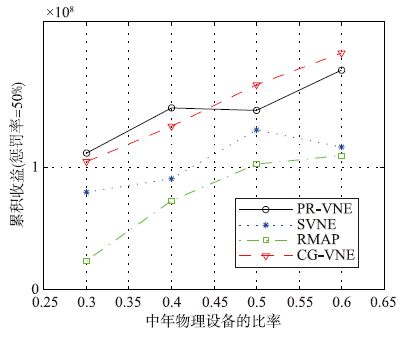
图 3评估了仿真结束时CP的收入G. 随着中年物理设备的比率增加,CG-VNE的收益呈直线上升的趋势. 当中年设备的比例大于45%后,CG-VNE的收益要高于其他3种算法的收益. 仔细分析其原因可知,G主要取决于VN的接受率(图 1)和物理故障导致的惩罚(图 2). 此外,需要指出的是,支付的惩罚总额低于接受新客户获得的收益. 然而,本文没有评估云提供商的坏名声对泊松过程到达率的影响. 本文认为,考虑云供应商的频繁故障将会增加本文方法的收益.
|
| 图 3 收益G Figure 3 The earnings G |
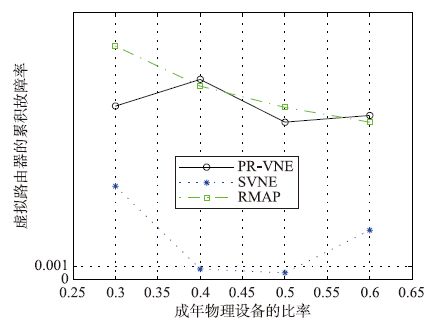
图 4中给出了受到物理故障影响的虚拟路由器的比率. 在图 4中,不管成年物理设备的比率如何变化,CG-VNE的数值为0,所以在图中没有给出(在Y轴对数标度中无法表示0). 这表明CG-VNE成功恢复了底层路由器故障导致的所有虚拟节点,要优于其他的3种算法.
|
| 图 4 受到故障影响的虚拟路由器的比率 Figure 4 Affected by the failure of the ratio of the virtual router |
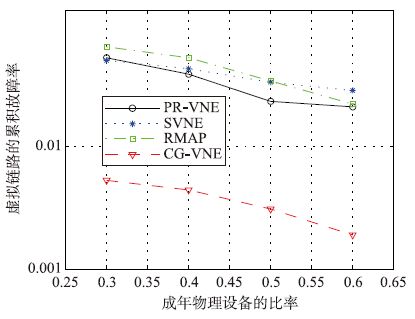
图 5给出了受到物理故障(路由器和链路)影响的虚拟链路的比率. 可以发现,与其他算法相比,CG-VNE显著降低了受到影响的虚拟链路的比率. 例如,当成年设备比率为30%时(即最老配置),CG-VNE将受到影响的虚拟链路的比率下降了88%左右. 因此可以认为,虚拟博弈Γ1和Γ2非常高效. 最后,在不考虑可靠性目标的情况下评估了本文方法的性能. 假设没有任何故障发生,SN保持工作. 为此,比较了基于协作博弈的高可靠性虚拟网络嵌入策略(CG-VNE)和其他相关算法实现的VN请求拒绝率和收入. 采用与文[13]相同的场景. 结果见表 1. 全面的仿真实验表明,除了D-VINE外,CG-VNE的性能优于其他所有虚拟网络嵌入算法. 实际上,CG-VNE的VN拒绝率为1.01±0.13%,而D-VINE只有0.65%. 后一种策略采用分割策略处理链路映射问题,处理方法与本文不同. 因此,D-VINE接受更多客户的概率更高. 尽管如此,CG-VNE的性能水平与基于分割策略的D-VINE非常接近.
|
| 图 5 受到故障影响的虚拟链路的比率 Figure 5 Affected by the failure of the ratio of virtual link |
本文研究了经证明为NP难题的可靠性VN嵌入问题,提出一种新的被动算法CG-VNE. 据研究所知,在本文之前还没有其他文献研究过VN环境的响应问题. 本文方法以博弈论为基础,设计了两种互相交替的IIG博弈来解决可靠性VN嵌入问题的复杂性. 该模型的目标是使云供应商的收入最大化,使SN故障导致的请求拒绝率最小化. 全面的仿真实验表明,CG-VNE在拒绝率、 CP收入和受到底层故障影响的VN率3个方面的性能要优于目前大多数主流算法.
| [1] | 张逢喆, 陈进, 陈海波, 等. 云计算中的数据隐私性保护与自我销毁[J]. 计算机研究与发展 , 2015, 48 (7) : 1155–1167. Zhang F Z, Chen J, Chen H B, et al. Lifetime privacy and self-destruction of data in the cloud[J]. Journal of Computer Research and Development , 2015, 48 (7) : 1155–1167. |
| [2] | 李德毅, 张天雷, 黄立威. 位置服务: 接地气的云计算[J]. 电子学报 , 2014, 42 (4) : 786–790. Li D Y, Zhang T L, Huang L W. A down-to-earth cloud computing: Location-based service[J]. Acta Electronica Sinica , 2014, 42 (4) : 786–790. |
| [3] | Rahman A, Liu X, Kong F. A survey on geographic load balancing based data center power management in the smart grid environment[J]. IEEE Communications Surveys & Tutorials , 2014, 16 (1) : 214–233. DOI:10.1109/SURV.2013.070813.00183 |
| [4] | 叶可江, 吴朝晖, 姜晓红, 等. 虚拟化云计算平台的能耗管理[J]. 计算机学报 , 2012, 35 (6) : 1262–1285. DOI:10.3724/SP.J.1016.2012.01262 Ye K J, Wu Z H, Jiang X H, et al. Power management of virtualized cloud computing platform[J]. Chinese Journal of Computers , 2012, 35 (6) : 1262–1285. DOI:10.3724/SP.J.1016.2012.01262 |
| [5] | Rahman M R, Boutaba R. SVNE: Survivable virtual network embedding algorithms for network virtualization[J]. IEEE Transactions on Network and Service Management , 2013, 10 (2) : 105–118. DOI:10.1109/TNSM.2013.013013.110202 |
| [6] | Chowdhury M, Rahman M R, Boutaba R. Vineyard: Virtual network embedding algorithms with coordinated node and link mapping[J]. IEEE/ACM Transactions on Networking (TON) , 2012, 20 (1) : 206–219. DOI:10.1109/TNET.2011.2159308 |
| [7] | Yang Y, Chen S Z, Li X, et al. Rmap: An algorithm of virtual network resilience mapping[C]//2011 7th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM). Piscataway, NJ, USA: IEEE, 2011: 1-4. |
| [8] | Soualah O, Fajjari I, Aitsaadi N, et al. PR-VNE: Preventive reliable virtual network embedding algorithm in cloud′s network[C]//2013 IEEE Global Communications Conference (GLOBECOM). Piscataway, NJ, USA: IEEE, 2013: 1303-1309. |
| [9] | Chowdhury M, Rahman M R, Boutaba R. Vineyard: Virtual network embedding algorithms with coordinated node and link mapping[J]. IEEE/ACM Transactions on Networking (TON) , 2012, 20 (1) : 206–219. DOI:10.1109/TNET.2011.2159308 |
| [10] | Halpern J Y, Pass R. Algorithmic rationality: Game theory with costly computation[J]. Journal of Economic Theory , 2015, 15 (6) : 246–268. |
| [11] | Srivastava V, Neel J O, MacKenzie A B, et al. Using game theory to analyze wireless ad hoc networks[J]. IEEE Communications Surveys and Tutorials , 2015, 7 (14) : 46–56. |
| [12] | Chuah C N. Characterization of Failures in an Operational IP Backbone Network[J]. IEEE/ACM Transactions on Networking , 2008, 16 (4) : 749–762. DOI:10.1109/TNET.2007.902727 |
| [13] | Fajjari I, Aitsaadi N, Pujolle G, et al. VNE-AC: Virtual network embedding algorithm based on ant colony metaheuristic[C]//2011 IEEE International Conference on Communications (ICC). Piscataway, NJ, USA: IEEE, 2011: 1-6. |
| [14] | Wang C, Yuan Y, Wang C, et al. Virtual bandwidth allocation game in data centers[C]//2012 International Conference on Information Science and Technology (ICIST). Piscataway, NJ, USA: IEEE, 2012: 682-685. |
| [15] | Sapuntzakis C P, Chandra R, Pfaff B, et al. Optimizing the migration of virtual computers[J]. ACM SIGOPS Operating Systems Review , 2012, 36 (11) : 377–390. |
| [16] | Egilmez H E, Civanlar S. An optimization framework for QoS-enabled adaptive video streaming over OpenFlow networks[J]. IEEE Transactions on Multimedia , 2013, 15 (3) : 710–715. DOI:10.1109/TMM.2012.2232645 |
| [17] | Zhu Y, Ammar M H. Algorithms for assigning substrate network resources to virtual network components[C]//25th IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies. Piscataway, NJ, USA: IEEE, 2006: 1-12. |



