1 引言
Buck型变换器是一种基本的电力电子变换器. 该类变换器可以采用输出电压闭环控制的单环路控制结构,也可以采用电压外环、 电流内环的双环路控制结构[1]. 主要控制目标是将输出电压稳定在给定值.
控制方案对变换器系统的动、 静态性能有重要影响[2]. 目前,线性控制如比例—积分(proportion-integration, PI)控制用于变换器,可以满足多数场合的应用要求. 同时电力电子变换器本身都具有很强的非线性,鉴于此,为进一步改善控制性能,近年来国内外学者对采用非线性控制方案的功率变换器进行了深入研究,例如滑模控制[3-5]、 反步控制[6]、 无源控制[7-9]和自适应控制[10-12]等. 模型参考自适应控制(model reference adaptive control, MRAC)是自适应控制的一个重要分支,可以用来解决性能规范由参考模型规定的控制问题,已经在电机、 电力系统以及飞行器等被控对象上得到实际应用,并取得了良好的控制效果[13]. 在MRAC方案下,控制系统可根据自适应律对控制器参数进行动态调节,使被控对象的动、 静态性能逼近给定的参考模型,这同样适用于输入电压变化范围较宽或电路参数存在变化的电力电子变换器.
目前,国内外学者对基于MRAC的电力电子变换器进行了一些研究: 文[14]基于Buck-Boost变换器的小信号模型和所选取的参考模型对控制器进行设计,利用递归最小二乘法估计不确定参数,实现了变换器的模型参考自适应数字控制方案; 为了使得Zeta变换器输出电压可调节并准确跟踪参考信号,文[15]将模型参考自适应控制与神经网络结合起来实现了对Zeta变换器输出电压的控制; 文[16]则在Buck-Boost变换器状态空间平均模型基础上提出了一种无源自适应控制策略. 现有研究基本证实了MRAC在电力电子变换器控制中的有效性. MRAC方案有多种,有基本的MIT方案、 基于李亚普诺夫稳定性理论和超稳定性理论的设计方案等. MIT方案是早期提出的MRAC方案,具有结构简单、 动态过程总偏差小、 偏差消除速率快、 在线计算量较小等优点,具有一定的工程实用价值. MIT MRAC方案下,参考模型和自适应控制器参数对控制性能影响较大,但是在变换器控制中,如何选取相关模型,以及如何配置其中的关键参数等问题现有文献讨论还不够充分,有必要做更深入的分析. 这里具体结合Buck变换器进行研究.
首先建立Buck变换器小信号模型,然后对MRAC方案进行设计,其中包括自适应律、 参考模型以及Buck变换器MIT方案的设计; 最后在Matlab/Sinulink环境下进行仿真验证. 本文提供的设计方案对其他类型的电力电子变换器的控制也具有一定参考价值.
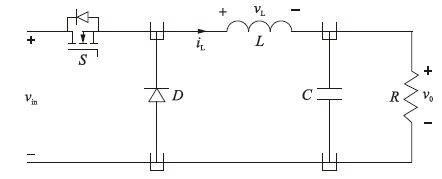
2 Buck变换器小信号模型 2.1 时域模型图 1为单相Buck变换器电路拓扑示意图.
|
| 图 1 Buck变换器电路拓扑图 Figure 1 Circuit topology of Buck converter |
vin、 vin分别为输入、 输出电压,L、 C分别为滤波电感和滤波电容,R为负载电阻.
假设电感电流处于连续模式,开关频率fs足够高,即满足低频假设和小纹波假设,则可得系统的平均变量状态方程[17],如式(1)所示.
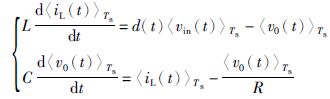
|
(1) |
式中,Ts=1/fs,为开关周期; d(t)为t时刻的开关导通占空比; 〈x(t)〉Ts代表变量在一个开关周期内的平均值.
在t时刻取小信号扰动,此时可将变换器中变量x(t)的平均变量〈x(t)〉Ts分解为直流分量X与交流小信号分量(t)两项之和. 对Buck变换器的各变量应用上述分解方法分解,可得式(2)所示方程组.
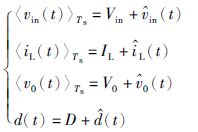
|
(2) |
其中,Vin、 V0、 IL和D分别为上述对应参数的直流分量,即各参数在t时刻的稳态值.
假设系统同时满足小信号假设,即满足式(3)所示的大小关系:
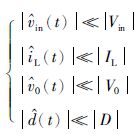
|
(3) |
将式(2)代入式(1),同时忽略小信号乘积项,可得系统时域模型,如式(4)所示.
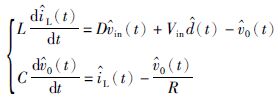
|
(4) |
对式(4)两边同时进行拉普拉斯变换,可得式(5)和式(6)所示的频域模型.
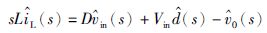
|
(5) |

|
(6) |
式(5)中令in(s)=0、 再由式(5)、 式(6)可以得到控制输出到输出电压之间的传递函数,如式(7)所示:
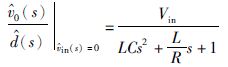
|
(7) |
式(7)即为设计电压环模型参考自适应控制所需的被控对象传递函数表达式.
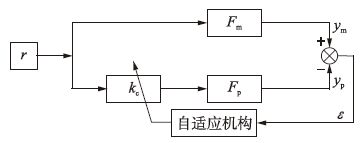
3 MRAC方案设计具有可调增益的自适应控制方案[18-19]结构图如图 2所示. 其中,r为输入信号,即给定参考信号; Fp为被控对象传递函数,即从控制输出到输出信号之间的传递函数; kc为可调增益; Fm为参考模型传递函数,人为设定; ym为参考模型的输出,即理想输出; yp为被控对象的输出,即实际输出.
|
| 图 2 MRAC系统结构图 Figure 2 Structure diagram of MRAC system |
如果实际输出和理想输出不相同,就会产生偏差ε,自适应控制就是利用这个偏差,通过一定的自适应律对参数kc进行动态调整,使得ε(t)尽可能接近0,从而使得实际输出尽可能地跟踪理想输出. 其中自适应律的设计是关键,直接影响控制器的参数收敛效果和系统稳定性. 由于这个方案是由美国麻省理工学院(MIT)最早提出来的,因此又称为MIT自适应方案.
3.1 MIT方案原理及控制器设计如图 2所示,引入广义误差ε(t),定义如下:
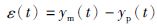
|
(8) |
设性能指标泛函为
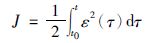
|
(9) |
现用梯度寻优法确定kc的调节规律,即系统的自适规律,使得J达到最小,同时limt→0 e(t)=0. 这里正反映了自适应控制的一个重要思想: 设计目的是使J尽可能小,而非kcFp→Fm[19]. 根据梯度法的性质可知,使J下降的方向是负梯度方向,因此参数kc的修正量为
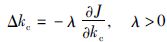
|
(10) |
则调整后的kc为
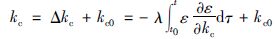
|
(11) |
式中,kc0为kc的初值,人为选取; λ为调节步长,通常为一个很小的正数. 将式(11)两边对时间t求导,得到:
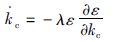
|
(12) |
求式(8)对kc的偏导数,并且考虑到ym与kc无关,可得:
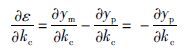
|
(13) |
把式(13)代入式(12),可得:
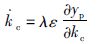
|
(14) |
经过模型匹配过程可得:
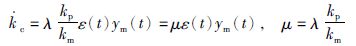
|
(15) |
其中,kp、 km分别为被控对象和参考模型传递函数中的增益系数,μ为最终调节步长. kp是不确定的,则μ同样也是不确定的,但是在实际中,μ用一个较小的常数替代即可. 由式(15)得可调增益kc的自适应律为
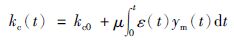
|
(16) |
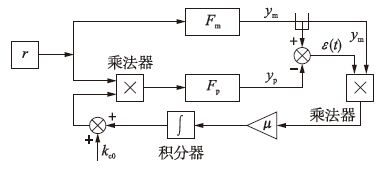
结合自适应律和图 2可以得到MIT MRAC方案结构图,如图 3所示.
图 3所示方案中,调节步长μ对系统的收敛有显著影响. 总体上来说,增大μ的取值,不利于系统收敛,甚至会引起振荡; 减小μ的取值,有利于系统稳定,但是会延长调节时间. 实际设计中,可以结合仿真,从较小取值开始,在保证系统收敛的情况下,适当增大μ的取值,直到取得合适的收敛速度.
|
| 图 3 MIT MRAC方案结构图 Figure 3 Structure diagram of MIT MRAC scheme |
初值kc0不影响系统输出的稳态值,只影响系统运行初期的过渡过程. 具体设计中,可以参考仿真结果进行设置. 另外,为防止输出过冲太大,可对控制器输出进行适当限幅.
3.2 参考模型的设计参考模型是决定系统动静态性能的重要环节. 选取合适的参考模型有利于系统表现出良好的性能. 为了真正实现较小的ε(t),达到良好的跟踪效果,可将Fm与Fp取相同阶数. 结合式(7)所示的Buck变换器控制—输出传递函数的表达形式,这里采用典型的二阶系统模型作为参考模型Fm的设计目标.
典型的二阶系统模型[20]如式(17)所示,其中ξ为系统的阻尼比,ωn为系统的固有频率. 该模型的直流稳态增益为1.
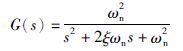
|
(17) |
考虑到欠阻尼(0<ξ<1)二阶系统的单位阶跃响应为一个收敛响应,系统性能稳定,并且系统稳态误差ess为0,所以这里选用欠阻尼系统.
单位阶跃信号输入下系统的超调量σ、 上升时间tr和调节时间ts等均是二阶系统的重要性能指标,可以作为二阶模型参数设计的依据. 超调量和快速性指标互相制约,为兼顾响应的快速性,在设计二阶系统时,有必要允许一定的超调量.
结合欠阻尼条件下各性能指标之间的关系式,参考模型的设计步骤如下:
1) 先给定合适的超调量,然后按照式(18)所示的阻尼比表达式确定阻尼比. 通常选取σ%=1.5%~25.4%[20-21].
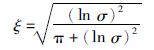
|
(18) |
2) 根据给定的上升时间指标和1)中得到的阻尼比参数,利用式(19)求得系统的固有频率ωn.
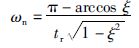
|
(19) |
3) 将求得的ξ、 ωn代入式(20),确认调节时间ts是否满足要求,其中Δ为允许的误差带宽度.
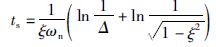
|
(20) |
按照上述设计步骤,这里给定超调量约为5%,代入式(18)得ξ=0.687 7. 设定上升时间为0.5 s, 由式(19)可得固有频率ωn=6.42 rad/s. 将ξ、 ωn代入式(20),可求得调节时间ts=0.959 s, 其中,Δ取0.02. 由以上数据可知相关性能参数基本符合实际要求. 所以最终参考模型如式(21)所示.
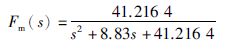
|
(21) |
Buck变换器输出电压闭环MIT MRAC控制方案的基本架构如图 4所示.
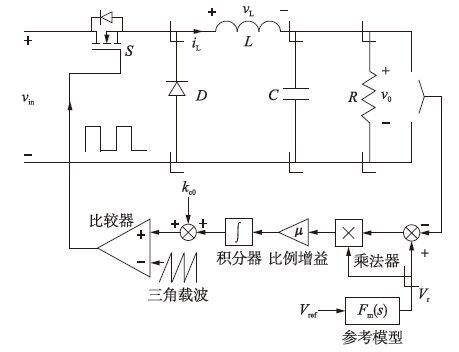
|
| 图 4 基于MIT MRAC方案的电压控制基本架构图 Figure 4 Basic architecture diagram of voltage control based on MIT MRAC scheme |
主要工作原理如下: Vref为输出电压参考,参考模型Fm(s)的输出Vr与采样的输出电压vin作差,产生的误差信号通过乘法器与Vr相乘,相乘后得到的信号经过比例增益(调节步长)和积分器再与可调增益kc的初值kc0相加作为调制信号,此后,调制信号作为比较器的正相输入与负相输入的三角载波进行比较,得到具有一定占空比的方波控制信号控制开关管S的导通与关断,实现电路整体的正常运作.
系统具有如下参数: 输入电压vin=400 V; 电感L=1 mH; 电容C=2 000 μF; 负载电阻R=10 Ω,开关频率fs=20 kHz(同时也为三角载波频率).
将上述系统参数带入式(7)可得被控对象传递函数Fp(s),如式(22)所示:
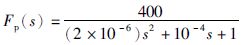
|
(22) |
下面将通过频域和时域的仿真进行相关验证.
4 仿真验证在Matlab/Simulink环境下进行了仿真,仿真包括以下几个方面内容:
1) 参考模型的验证;
2) 电压环MIT MRAC方案有效性验证;
3) MIT控制器关键参数取值对系统性能影响验证.
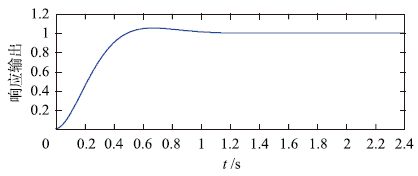
4.1 参考模型的验证下面对3.2节所设计的参考模型进行验证. 以单位阶跃信号为输入,观察所选参考模型的响应效果,分析各动态性能指标. 响应曲线如图 5所示.
|
| 图 5 参考模型单位阶跃响应曲线 Figure 5 Unit step response curve of reference model |
观察和分析曲线可知,超调量、 上升时间和调节时间与设计指标基本一致,满足要求.
4.2 电压环MIT MRAC方案有效性验证按照3.2节设计的二阶参考模型和3.3节中系统参数的设定,进行了频域仿真和时域仿真.
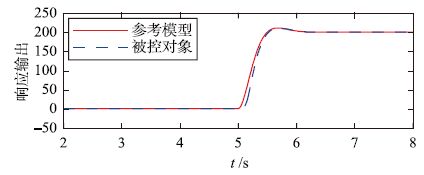
4.2.1 频域仿真输入信号(输出电压参考)是一个阶跃信号,初始值为0,终值为200,阶跃时间为5 s, 调节步长μ为0.000 002,kc的初值kc0=0,仿真时间为10 s. 仿真结果如图 6所示.
|
| 图 6 频域仿真结果 Figure 6 Result of frequency-domain simulation |
频域仿真结果证实,在所选取的参考模型下,被控对象输出跟踪参考模型输出的效果良好.
4.2.2 时域仿真在恒定和变化的输出电压参考下分别对不变负载、 突加负载100%和突卸负载50%三种情况进行时域仿真,观察和分析输出电压的控制效果,验证MIT MRAC方案的有效性.
其中调节步长μ=0.000 2,kc的初值kc0=0,仿真时间为10 s, 在t=5 s时改变负载.
1) 输出电压参考为恒定200 V.
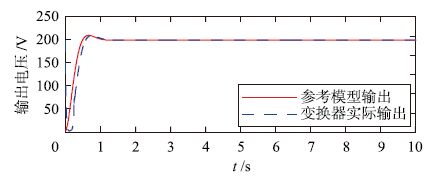
不变负载下输出电压和参考模型输出波形如图 7所示.
|
| 图 7 不变负载下输出电压波形 Figure 7 Waveform of output voltage under constant load |
图 7证实,对于负载不变的情况,变换器实际输出电压跟踪参考模型输出效果良好,输出电压能够快速稳定在给定值.
突加负载和突卸负载下输出电压和参考模型输出波形如图 8和9所示.
|
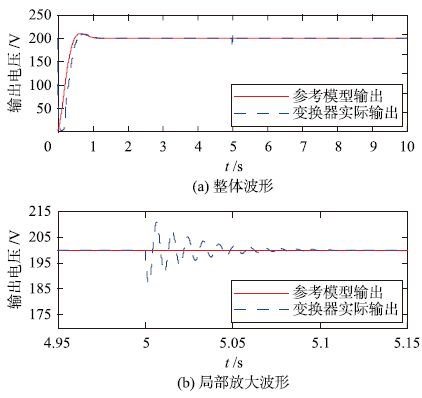
| 图 8 突加负载100%下输出电压的波形 Figure 8 Waveforms of output voltage under sudden increase of load by 100% |
|
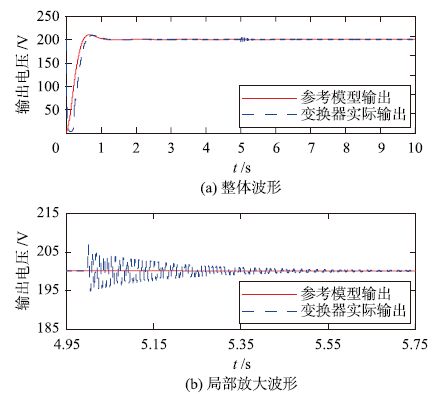
| 图 9 突卸负载50%下输出电压的波形 Figure 9 Waveforms of output voltage under sudden decrease of load by 50% |
图 8和图 9证实,对于负载突变的情况,变换器实际输出电压可以很好地跟踪参考模型输出. 负载突变后输出电压振荡幅度较小,持续时间短,突加负载后0.1 s左右重新稳定在给定值,突卸负载后0.6 s左右重新稳定在给定值,具有良好的快速性能.
2) 输出电压参考输入为方波脉冲信号,谷值为150,幅值为250,周期为5 s, 脉冲宽度为40%. 在t=5 s时改变负载.
不变负载下输出电压和参考模型输出波形如图 10所示.
|
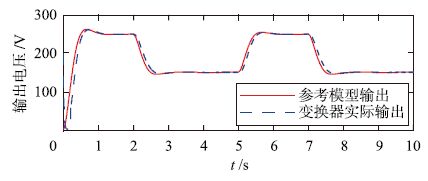
| 图 10 不变负载下输出电压的波形 Figure 10 Waveform of output voltage under constant load |
图 10证实,在负载不变的情况下,变换器实际输出电压可以较好地跟踪参考模型输出,输出电压能够快速稳定在给定值.
突加负载和突卸负载下输出电压和参考模型输出波形如图 11和12所示.
|
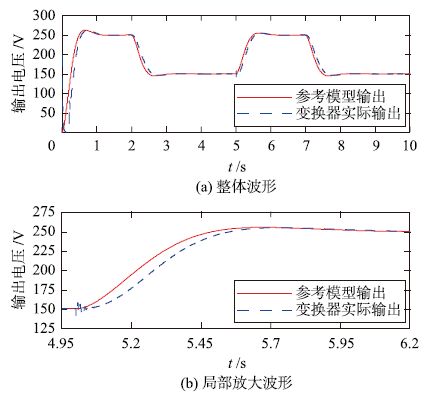
| 图 11 突加负载100%下输出电压的波形 Figure 11 Waveforms of output voltage under sudden increase of load by 100% |
图 11和12证实,在负载突变的情况下,变换器实际输出电压跟踪参考模型输出效果良好. 负载突变后输出电压振荡幅度小,持续时间较短,突加和突卸负载后1 s左右重新稳定在给定值,稳定快速.
|
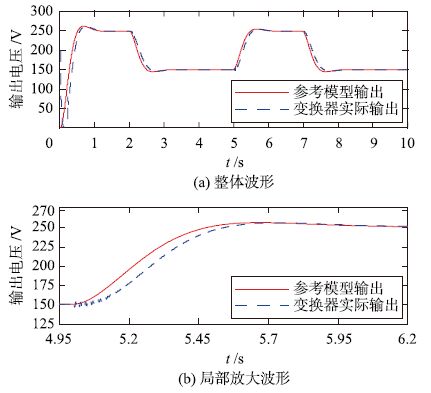
| 图 12 突卸负载50%下输出电压的波形 Figure 12 Waveforms of output voltage under sudden decrease of load by 50% |
时域仿真结果表明,在所选参考模型和控制器参数下,对于输入或负载变化的情况,输出电压能够较好地跟踪参考模型的输出,快速稳定在给定值,并且具有良好的性能. 系统的稳定性和动静态性能良好,抗干扰能力强,参考模型的选取合理.
频域和时域仿真表明了MIT MRAC方案用于Buck变换器输出电压控制的可行性和有效性.
4.3 MIT控制器关键参数取值对系统影响验证这里主要验证MIT控制器的关键参数调节步长μ和可调增益kc的初值kc0的不同取值对系统性能的影响,即验证3.1节中相关结论的正确性.
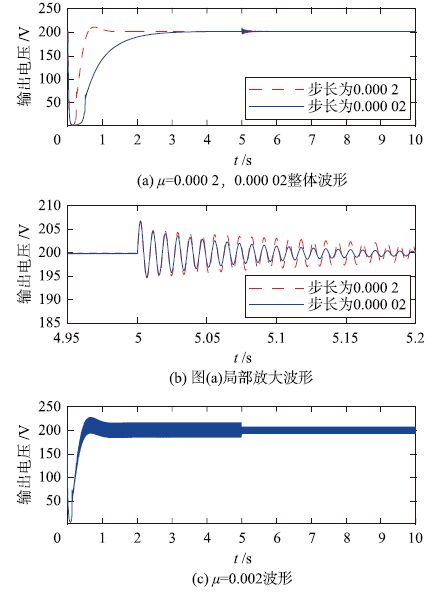
1) 相同初值,不同步长. 这里同取初值kc0=0,调节步长μ分别取0.002、 0.000 2和0.000 02,观察在输出电压参考为恒定200 V突卸负载50%情况下三种不同调节步长所对应的输出电压的波形. 仿真时间为10 s. 仿真结果如图 13所示.
|
| 图 13 不同调节步长下输出电压的波形 Figure 13 Waveforms of output voltage under different adjusting step |
通过对图 13的观察和分析可知,调节步长μ取0.000 2和取0.000 02相比,具有更好的快速性能,输出电压稳定在给定值所需时间较短,但是负载突变后输出电压振荡幅度较大; μ取0.002时整个过程趋于振荡,稳定性能较差.
仿真结果表明,增大调节步长μ不利于系统稳定,甚至会引起系统振荡,但是参数调节时间较短; 适当减小调节步长有利于系统稳定,但是会延长调节时间.
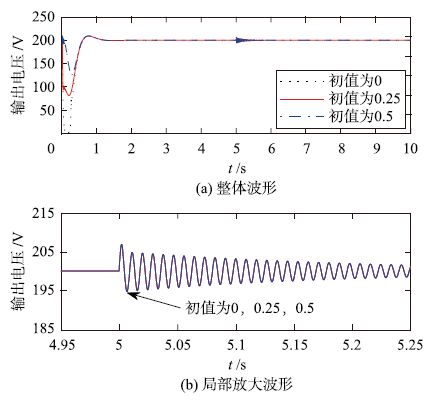
2) 相同步长,不同初值. 这里同取调节步长μ=0.000 2,可调增益kc初值kc0分别取0、 0.25和0.5,观察在输出电压参考为恒定200 V突卸负载50%情况下三种不同初值所对应的输出电压的波形,仿真时间为10 s, 仿真结果如图 14所示.
|
| 图 14 不同kc初值下输出电压的波形 Figure 14 Waveforms of output voltage under different initial value of kc |
图 14证实,初值kc0取0、 0.25和0.5三种情况下,除了系统初始状态下的过渡过程存在一定的差异,稳定后的性能基本相同.
仿真结果表明,初值kc0只是影响系统初始时刻的过渡过程,并不影响系统稳态后的增益系数,也不影响系统的稳态输出.
5 结论本文对基于MIT MRAC电压控制的Buck变换器进行研究和仿真,得到如下结论:
1) MIT MRAC方案适用于Buck变换器的输出电压闭环控制;
2) 参考模型是影响控制系统动静态性能的关键因素,实际中可根据期望的性能指标设计合适的参考模型;
3) 系统稳定后,实际输出与理想输出相等;
4) 可调增益kc的初值kc0影响系统初始时刻的过渡过程,不影响系统的稳态输出;
5) 参数调节步长μ对系统稳定有重要影响,在适当范围内减小调节步长有利于系统稳定,但会延长调节时间.
| [1] | 周国华, 许建平. 开关变换器调制与控制技术综述[J]. 中国电机工程学报 , 2014, 34 (6) : 815–831. Zhou G H, Xu J P. A review of modulation and control techniques for switching converters[J]. Proceedings of the CSEE , 2014, 34 (6) : 815–831. |
| [2] | 卢伟国, 赵乃宽, 郎爽, 等. DC/DC降压变换器非线性控制及纹波补偿策略[J]. 中国电机工程学报 , 2013, 33 (33) : 35–41. Lu W G, Zhao N K, Lang S, et al. Nonlinear control of a DC/DC buck converter and its ripple compensation strategy[J]. Proceedings of the CSEE , 2013, 33 (33) : 35–41. |
| [3] | Tan S C, Lai Y M, Tse C K. Indirect sliding mode control of power converters via double integral sliding surface[J]. IEEE Transactions on Power Electronics , 2008, 23 (2) : 600–611. DOI:10.1109/TPEL.2007.915624 |
| [4] | 吴宇, 皇甫宜耿, 张琳, 等. 大扰动Buck-Boost变换器的鲁棒高阶滑模控制[J]. 中国电机工程学报 , 2015, 35 (7) : 1740–1748. Wu Y, Huangfu Y G, Zhang L, et al. A robust high order sliding mode for Buck-Boost converters with large disturbances[J]. Proceedings of the CSEE , 2015, 35 (7) : 1740–1748. |
| [5] | 倪雨, 许建平, 于海坤, 等. 控制受限滑模控制Buck变换器设计[J]. 中国电机工程学报 , 2010, 30 (18) : 26–32. Ni Y, Xu J P, Yu H K, et al. Design of sliding mode control Buck converter with bounded input[J]. Proceedings of the CSEE , 2010, 30 (18) : 26–32. |
| [6] | 王艳, 陈进军, 纪志成. 基于SG的Buck变换器自适应反步法控制[J]. 控制工程 , 2009, 16 (6) : 662–665. Wang Y, Chen J J, Ji Z C. Adaptive backstepping control for buck converter via system generator[J]. Control Engineering of China , 2009, 16 (6) : 662–665. |
| [7] | 王久和. 基于EL模型的Boost型DC/DC变换器无源控制器[J]. 北京信息科技大学学报: 自然科学版 , 2012, 27 (5) : 17–20. Wang J H. Passivity based controller of Boost type DC/DC converter based on EL model[J]. Journal of Beijing Information Science and Technology University: the Science edition , 2012, 27 (5) : 17–20. |
| [8] | Lee T S. Lagrangian modeling and passivity-based control of three-phase AC/DC voltage-source converters[J]. IEEE Transactions on Industrial Electronics , 2004, 5 (4) : 892–902. |
| [9] | 李鑫, 李乃文, 杨桢, 等. 零电流开关准谐振Boost变换器的无源控制[J]. 电力电子技术 , 2012, 46 (2) : 15–17. Li X, Li N W, Yang Z, et al. Passivity-based control of zero-current-switching quasi-resonant Boost converter[J]. Power Electronics , 2012, 46 (2) : 15–17. |
| [10] | 谢桢, 付立军, 肖飞, 等. 直流变换器模式快速识别PI自适应控制策略[J]. 电机与控制学报 , 2013, 17 (1) : 25–30. Xie Z, Fu L J, Xiao F, et al. Fast mode identification PI adaptive control strategy for DC/DC converter[J]. Electric Machines and Control , 2013, 17 (1) : 25–30. |
| [11] | 郭鑫, 任海鹏. 三相PWM变换器的负载自适应控制[J]. 电子学报 , 2015, 43 (10) : 2088–2094. Guo X, Ren H P. Load adaptive control for three-phase PWM converter[J]. Acta Electronica Sinica , 2015, 43 (10) : 2088–2094. |
| [12] | 吴延华, 邱丽. 基于DSP自适应模糊控制的直流电源研究[J]. 机电工程 , 2012, 29 (12) : 1467–1470. Wu Y H, Qiu L. Design of DC power based on DSP self-adaptive fuzzy control[J]. Journal of Mechanical & Electrical Engineering , 2012, 29 (12) : 1467–1470. |
| [13] | 周涛, 王磊. 基于跟踪微分器的模型参考自适应控制[J]. 电光与控制 , 2012, 19 (10) : 46–49. Zhou T, Wang L. Model reference adaptive control based on tracking differentiators[J]. Electronics Optics & Control , 2012, 19 (10) : 46–49. |
| [14] | Li Y F, Tsai M F, Tseng C S, et al. Model reference adaptive control design for the Buck-Boost converter[C]//Annual Conference on IEEE Industrial Electronics Society. Piscataway, NJ, USA: IEEE, 2012: 543-548. |
| [15] | Moaveni B, Abdollahzadeh H, Mazoochi M. Adjustable output voltage zeta converter using neural network adaptive model reference control[C]//2nd International Conference on Instrumentation Control and Automation. Piscataway, NJ, USA: IEEE, 2011: 552-557. |
| [16] | 王丙元, 冯辉. 无源自适应控制Buck-Boost变换器研究[J]. 电力电子技术 , 2012, 46 (11) : 32–35. Wang B Y, Feng H. Research on the Buck-Boost converter adopting a passivity-based adaptive control strategy[J]. Power Electronics , 2012, 46 (11) : 32–35. |
| [17] | 程红, 王聪, 王俊. 开关变换器建模控制及其控制器的数字实现[M]. 北京: 清华大学出版社 ,2013 : 25 -35. Cheng H, Wang C, Wang J. Modeling、 control and digital controller implementation of switching power converters[M]. Beijing: Tsinghua University Press , 2013 : 25 -35. |
| [18] | 李言俊, 张科. 自适应控制理论及应用[M]. 西安: 西北工业大学出版社 ,2005 : 40 -44. Li Y J, Zhang K. Adaptive control theory and applications[M]. Xi′an: Northwestern Polytechnical University Press , 2005 : 40 -44. |
| [19] | 韩正之, 陈彭年, 陈树中. 自适应控制[M]. 北京: 清华大学出版社 ,2014 : 64 -71. Han Z Z, Chen P N, Chen S Z. Adaptive control[M]. Beijing: Tsinghua University Press , 2014 : 64 -71. |
| [20] | 胡寿松. 自动控制原理[M]. 5版. 北京: 科学出版社 ,2007 : 76 -80. Hu S S. The principle of automatic control[M]. 5th ed. Beijing: Science Press , 2007 : 76 -80. |
| [21] | 袁安富. 自动控制原理[M]. 北京: 北京交通大学出版社 ,2008 : 62 -85. Yuan A F. Automatic control principle[M]. Beijing: Beijing Jiaotong University Press , 2008 : 62 -85. |



