2. 国家信息农业工程技术中心, 江苏 南京 210095
2. National Engineering and Technology Center for Information Agriculture, Nanjing 210095, China
1 引言
迁移学习是运用已存在的知识对不同但相关领域问题进行求解的一类新型机器学习方法[1]. 相比于传统的机器学习方法,迁移学习的训练数据和测试数据间没有同分布要求,更适用于大数据时代数据变化快、 样本时效性强的特点,是近年来机器学习领域的研究热点[2-5]. 基于特征的迁移是迁移学习的常用方法,根据对样本特征的处理又可以分为基于特征选择和特征映射方法: 基于特征选择的方法首先提取不同领域的共有特征,再利用共有特征进行知识迁移[6-7]; 而基于特征映射的方法将不同领域样本的特征由原始高维特征空间映射到低维潜在特征子空间(latent feature subspace)中,使得不同领域样本的特征分布在子空间内相似,进而可以基于子空间特征训练得到同时适用于源领域和目标领域的预测模型[8-11].
尽管迁移学习算法理论研究已趋于成熟,但大多数迁移学习算法只能够解决单个类别标记的“单标记数据”迁移问题,而现实世界中还包含许多被标注了多个类别标记的“多标记数据”[12]. 如何从相关领域的多标记数据中提取知识迁移到目标问题域中是迁移学习急需解决的问题.
目前针对多标记数据的迁移学习主要有两类方法: 一类方法将多标记迁移学习问题转化为多个单标记迁移学习问题处理[13]. 该方法对多标记数据中的每一个类别标记采用独立的单标记迁移学习算法学习并预测,不同类别标记的分类算法间彼此独立. 然而,一个多标记数据包含的不同标记之间往往存在相关联的语义,研究发现忽视标记间的关联关系而对每个标记独立学习不利于算法的学习和预测[14]. 另一类方法将已有的单标记迁移学习算法或多标记传统机器学习算法改进为多标记迁移学习算法,使其能够处理多标记迁移学习问题. Cheng[15]针对多模态多标记数据的迁移学习问题,将Lasso模型改进为多模态多标记特征选择模型,模型提取不同模态多标记数据间的公共特征,并采用多核相关向量机(relevance vector machine, RVM)基于公共特征进行预测. Fu[16]针对多标记数据的零样本学习问题,采用深度学习构造样本的文本语义表示,并通过构造标记关系的幂集与样本语义文本的KNN图建立样本与标记间的关系. Han[17]针对多标记迁移学习中特征向量维数过高的问题提出基于稀疏表示的多标记迁移学习算法,将源领域特征与标记的关联关系映射到低维子空间中,目标领域通过与源领域共享子空间的方式学习源领域的知识. 上述多标记迁移学习算法均通过共享子空间的方法实现知识迁移,但由于源领域与目标领域样本的原始特征分布不同,相应子空间内的潜在特征分布也可能不同,此时源领域子空间中的潜在特征不一定适用于目标领域,无法促进目标领域的学习.
为了减小源领域与目标领域的多标记数据在子空间内的分布差异,本文提出一种基于最大均值差异的多标记迁移学习算法(Multi-Label Transfer Learning via Maximum mean discrepancy, M-MLTL). 算法通过分解源领域的“特征—标记”关系矩阵将标记间的关联关系嵌入潜在特征子空间,目标领域与源领域通过共享子空间迁移知识; 采用最大均值差异(maximum mean discrepancy, MMD)[18]作为评价指标,最小化不同领域的子空间特征概率分布差异,从而充分利用源领域的数据.
2 最大均值差异假设分别存在一个满足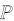
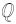
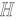
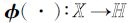
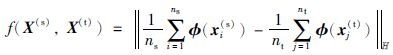
|
(1) |
MMD度量就是使用源域数据集与目标域数据集的总体均值之差来表示源域与目标域之间的分布差异. 目前MMD已被广泛应用于单标记迁移学习研究中[19-21],但仍没有被用于多标记迁移学习领域中.
3 基于最大均值差异的多标记迁移学习算法首先描述本文的问题,假设存在已标记源领域样本集D(s)={(x(s)1,y(s)1),…,(x(s)ns,y(s)ns)}和未标记的目标领域样本集D(t)={x(t)1,…,x(t)nt},构造用于预测目标领域的样本标记Y(t)=[y(t)1,…,y(t)nt]的预测模型,其中D(s)和D(t)的样本特征概率分布不同. 为叙述方便,表 1给出了本文中的常用符号.
| 符号 | 描述 |
| D(s),D(t) | 源/目标领域样本集 |
| X(s),X(t) | 源/目标领域样本特征矩阵 |
| Y(s),Y(t) | 源/目标领域样本标记矩阵 |
| Z(s),Z(t) | 源/目标领域样本潜在特征矩阵 |
| ns,nt | 源/目标领域样本数量 |
| d | 样本输入特征数量 |
| m | 样本类别标记数量 |
| g | 低维子空间特征数量 |
本文通过构造一个理想的潜在子空间,将标记间关系嵌入潜在特征中并保证源领域与目标领域的潜在特征分布相似. 如何将标记间关联关系嵌入潜在子空间及如何最小化子空间中的分布差异是本算法的两个关键问题.
3.1.1 潜在子空间嵌入
潜在特征表达了介于样本输入特征的低级语义和类别标记的高级语义间的中间语义,因此必须建立输入特征和类别标记间的关系. 基于上述考虑,算法构造“特征—标记”关系矩阵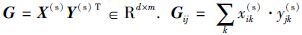
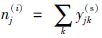
受潜在语义分析(latent semantic analysis, LSA)[22]启发,算法通过分解关系矩阵G将训练样本的输入特征和类别标记关系嵌入潜在子空间:
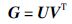
|
(2) |
其中U∈Rd×g,V∈Rm×g,g是潜在特征的个数,矩阵U的行向量ui是第i个输入参数的潜在特征表示. 类似地,矩阵V的行向量vj是第j个标记的潜在特征表示. 为方便求解,式(2)的矩阵分解问题可以表示成式(3)的优化问题:
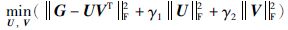
|
(3) |
其中,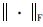
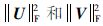
根据上述分解,可以得到源领域和目标领域数据在基U下的潜在特征,即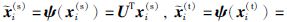
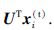
由于源领域和目标领域的样本特征分布不同,源领域和目标领域在子空间中的潜在特征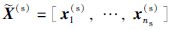
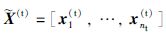
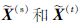
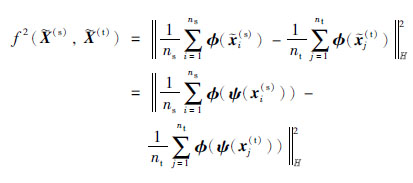
|
(4) |
其中,φ(·)是特征映射核函数,φ(ψ(·))也可以看作一个特征映射核函数. 这里构造一个线性映射核函数φ(ψ(x))=UTx,故有:
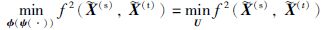
|
其中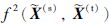
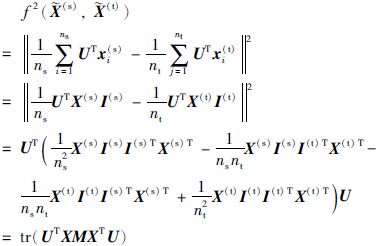
|
(5) |
其中,X=[X(s),X(t)]∈Rd×(ns+nt),I(s)=[1,…,1]T∈Rns×1,I(t)=[1,…,1]T∈Rnt×1,参数矩阵M构造如下:
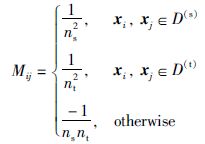
|
(6) |
结合式(3)和式(5),所提模型可描述为如下的优化问题:
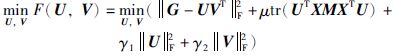
|
(7) |
其中μ≥0.
3.2 优化问题求解优化问题(7)有两个待优化变量U、 V,当固定U时目标问题是一个关于V的凸优化问题,反之亦然. 因此,本文拟采用交替迭代算法来求解,其求解过程如下:
步骤1 固定U求解V. 令F(U,V)关于V的偏导数为0,得到:
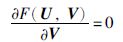
|
(8) |
经过化简,得到关于VT的线性方程组:
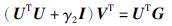
|
(9) |
由于UTU+γ2I是对称正定的,该方程可以采用共轭梯度法(Conjugate Gradient method, CG)[23]求解.
步骤2 固定V求解U. 与求解V类似,令F(U,V)关于U的偏导数为0,得到:
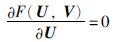
|
(10) |
通过矩阵变换得到:
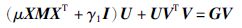
|
(11) |
上述方程是一个Sylvester方程,可以利用Bartels-Stewart算法[24]求解.
步骤3 重复步骤1~2,直到收敛.
3.3 算法步骤经上述分析,所提算法详细步骤描述如下:
| input 源领域样本输入矩阵X(s)∈Rd×ns和标记矩阵Y(s)∈{0,1}m×ns; 目标领域样本输入特征矩阵X(t)∈Rd×nt; 控制参数μ、 γ1和γ2,潜在特征的数量g. |
| Step 1 计算子空间矩阵U和V: G=X(s)Y(s)T 随机初始化矩阵U和V; repeat U不变,用CG算法求解式(9)中的矩阵V; V不变,用Bartels-Stewart算法求解式(11)中的矩阵U; until 收敛. Step 2 计算样本的潜在特征: (s)=UTX(s),(t)=UTX(s). Step 3 采用基分类算法预测目标领域样本类别标记Y(t). 采用RankSVM[ |
| output 目标领域样本的预测标记矩阵Y(t). |
所提模型的求解主要包括式(9)中线性方程的求解与式(11)中Sylvester方程的求解两个部分. 其中CG时间复杂度为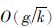
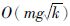
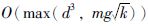
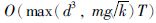
本文采用两个已被广泛认可的多标记图像数据集Corel5k[25]和ESPGame[26]构造实验数据集,选择4种对比算法基于5项评价指标验证本文所提模型的预测精度和计算时间. 本节首先对实验数据集、 评价指标和对比算法做详细介绍,再结合实验结果从分类精度、 关键参数和样本数量对算法的影响及计算时间三个方面分析所提算法的性能.
4.1 实验数据集构造本文采用Corel5k和ESPGame交替作为源领域和目标领域组成实验数据集“Corel5k vs ESPGame”和“ESPGamevs Corel5k”. 其中,Corel5k包含了5 000张图像和260个类别关键字,每张图像被手工标注1~5个关键字. ESPGame数据集包含的图像比Corel5k更多样,除了照片还包括商标、 涂鸦等类型的图像.
本文实验选取上述两个数据集共有的10个标记作为目标标记,图像的特征采用文[27]中提取的Dense SIFT视觉描述子. 从两个样本集中各随机抽取1 200个样本作为实验样本.
4.2 评价指标与单标记学习算法不同,多标记学习算法不仅会输出一个分类函数h∶X→2m,通常还会输出一个标记排序函数rank(xi,yji),一个理想的函数rank对于所有yji=1且yhi=0的情况都满足rank(xi,yji) <rank(xi,yhi). 为了能够从多个方面综合反映算法的预测效果,本文选取了5个目前被广泛采用的多标记学习评价指标[19, 28]: Hamming Loss、 Ranking Loss、 One Error、 Coverage、 Average Precision. 其中,Hamming Loss是针对分类函数h准确率的评价指标,Hamming Loss值越小表示算法的分类越准确; 其余4个指标用于评价排序函数rank的效果,Average Precision值越大表示函数rank的预测越好,其余的3个指标(Ranking Loss、 One Error、 Coverage)值越小说明排序函数rank的预测越好.
4.3 对比算法介绍为验证本文所提算法的性能,本文选择了以下4个多标记算法(见表 2)作为对比. 各算法分别采用不同的降维方法,但都采用线性核函数的RankSVM[29]作为基础分类器. 其中BL(base line)是原始RankSVM分类算法,该算法直接利用图像的Dense SIFT视觉描述子作为输入特征进行分类; LIFT(multi-label learning with Label spec IficFeaTures)[30]是目前最新的多标记学习算法,算法通过构造新的标记特征表示标记间关系; S-MLTL(Multi-Label Transfer Learning with Sparse representation)[17]是典型的多标记迁移学习算法,算法通过共享潜在子空间迁移知识; M-MLTL是本文提出的多标记迁移学习算法,本算法相较于S-MLTL进一步考虑了源领域与目标领域的分布差异; 为了验证MMD正则项对算法学习效果的影响,在实验中令μ=0得到M-MLTL算法的对比算法MLTL. MLTL算法不包含MMD正则项,仅通过分解关系矩阵构造低维子空间. 本实验中M-MLTL算法的参数μ取值为30,其它对比算法的参数设置均采用原文中的默认值.
4.4 多标记图像分类5种多标记算法的图像分类结果如表 2所示,评价指标的最优结果被加粗表示. 由表 2可知,在数据集“Corel5k vs ESPGame”上,新算法的Ranking Loss、 One Error、 Coverage、 Average Precision四个评价指标都取得了最好的效果,但Hamming Loss指标上M-MLTL与MLTL、 LIFT和BL算法相比没有明显的优势. 在数据集“ESPGame vs Corel5k”上,新算法的Hamming Loss、 Ranking Loss、 Coverage三个评价指标取得了最好的效果,但S-MLTL算法在One Error和Average Precision两个评价指标上略优于M-MLTL.
| 数据集 | 评价指标 | 算法 | ||||
| M-MLTL | MLTL | S-MLTL | LIFT | BL | ||
| Corel5k vs ESPGame | Hamming Loss↓ | 0.110±0.000 | 0.110±0.000 | 0.198±0.035 | 0.110±0.000 | 0.115±0.000 |
| Ranking Loss↓ | 0.449±0.005 | 0.480±0.018 | 0.545±0.000 | 0.534±0.020 | 0.576±0.000 | |
| One Error↓ | 0.873±0.004 | 0.903±0.018 | 0.941±0.000 | 0.927±0.008 | 0.940±0.000 | |
| Coverage↓ | 4.218±0.046 | 4.506±0.161 | 5.118±0.000 | 4.946±0.171 | 5.351±0.000 | |
| Average Precision↑ | 0.326±0.003 | 0.319±0.003 | 0.270±0.000 | 0.266±0.005 | 0.240±0.000 | |
| ESPGamevsCorel5k | Hamming Loss↓ | 0.103±0.000 | 0.107±0.001 | 0.179±0.000 | 0.107±0.006 | 0.107±0.000 |
| Ranking Loss↓ | 0.602±0.009 | 0.613±0.006 | 0.677±0.018 | 0.657±0.026 | 0.679±0.000 | |
| One Error↓ | 0.950±0.006 | 0.958±0.000 | 0.884±0.018 | 0.951±0.015 | 0.971±0.000 | |
| Coverage↓ | 5.459±0.078 | 5.557±0.055 | 6.130±0.161 | 5.945±0.246 | 6.149±0.000 | |
| Average Precision↑ | 0.227±0.005 | 0.218±0.000 | 0.242±0.003 | 0.203±0.018 | 0.186±0.000 | |
| 数据集 | 评价指标 | 算法 A1∶M-MLTL,A2∶MLTL,A3∶S-MLTL,A4∶LIFT,A5∶BL |
| Corel5k vs ESPGame | Hamming Loss | A1=A2=A4=A5>A3 |
| Ranking Loss | A1>A2>A4>A3>A5 | |
| One Error | A1>A2>A4>A5>A3 | |
| Coverage | A1>A2>A4>A3>A5 | |
| Average Precision | A1>A2>A3>A4>A5 | |
| ESPGame vs Corel5k | Hamming Loss | A1>A5>A2>A4>A3 |
| Ranking Loss | A1>A2>A4>A3>A5 | |
| One Error | A3>A1>A4>A2>A5 | |
| Coverage | A1>A2>A4>A3>A5 | |
| Average Precision | A3>A1>A2>A4>A5 | |
| 综合排序 | A1(38)>A2(27)>A4(19)>A3(17)>A5(8) | |
为了更直观地比较各项评价指标上算法的表现,本文综合两个数据集的结果,对每项评价指标上所有算法的结果排序,用A1>A2表示在该项指标下算法A1优于算法A2. 根据排序结果对每个算法打分,算法在某个指标中排第i名则获5-i分,最后以算法在所有指标上的得分总和作为该算法的综合评分,排序结果见表 3. 算法综合表现排名由高到低依次为M-MLTL、 MLTL、 LIFT、 S-MLTL、 BL,其中S-MLTL与LIFT差距不大. 值得注意的是,M-MLTL算法的各项指标都优于MLTL算法,说明MMD正则项对算法的学习效果起到了积极作用. LIFT和S-MLTL算法在不同数据集的各项指标上各有优劣但综合排名相近,虽然均高于没有经过降维操作的BL算法但综合表现低于本文所提算法,这是因为这2种算法在降维的过程中没有考虑不同领域数据在子空间中的特征分布差异,所以分类效果不理想.
表 4提供了两组实验样例及各算法的分类结果. 在左边一组样例中,测试样本的期望标记是“sand, sea”,该测试样本与该组第2张训练样本相似,与第1张训练样本差异较大. 因此,LIFT和BL作为普通多标记的学习算法仅识别了与第2张训练样本相同的标记“sand”; 而M-MLTL、 MLTL和S-MLTL三种多标记迁移学习算法都采用了分解“特征—标记”关系矩阵的子空间构造方法,可以通过对该组第1张训练样本的学习放大“sand”和“sea”在子空间的关联特征,进一步识别“sea”标记. 在右边一组样例中,训练样本普遍较灰暗,而测试样本较明亮,这样的特征分布差异导致没有考虑不同领域特征分布差异的MLTL等算法未能识别任何标记,而M-MLTL引入MMD作为指标,通过缩小训练样本与测试样本在子空间中的特征分布差异,成功识别所有标记. 上述两组实验样例说明: 通过分解“特征—标记”关系矩阵构造子空间的方法能够发掘标记间的关联特征; 通过引入MMD正则项减小训练样本与测试样本在子空间中的分布差异,能够有效提高迁移学习算法的分类精度. MMD作为指标,通过缩小训练样本与测试样本在子空间中的特征分布差异,成功识别所有标记. 上述两组实验样例说明: 通过分解“特征—标记”关系矩阵构造子空间的方法能够发掘标记间的关联特征; 通过引入MMD正则项减小训练样本与测试样本在子空间中的分布差异,能够有效提高迁移学习算法的分类精度.
4.5 参数μ对分类效果的影响MMD正则项是本模型的关键成分,其对目标函数值的影响受参数μ控制. 为了讨论参数μ对算法分类效果的影响,本次实验令μ的取值以5为步长由5逐步增加到50. 算法在“Corel5k vs ESPGame”数据集上的各项指标变化见图 1. 其中,参数μ取值的变化对所有指标均有不同程度的影响,具体表现如下:
1) 当μ<25时,随着μ的增大所有指标都有提升,这个阶段μ取值较小,MMD正则项没有完全发挥作用;
2) 当μ>30时,随着μ的增大所有指标都不断下降,这个阶段μ取值过大,使得目标函数中除MMD正则项的其它部分(如“特征—标记”关系矩阵分解)被忽视.
综上,在该数据集上,当μ∈[25, 30]时算法性能最佳. 综合考虑各评价指标,本文实验中可取μ=30.

|
| 图 1 参数μ对分类效果的影响 Figure 1 Influence on the classification results with different parameter μ |
源领域样本数量是迁移学习算法效果的重要影响因素,因此当源领域样本数量增加时,算法分类效果的变化. 实验采用“Corel5k vs ESPGame”数据集,随机抽取500~1 200个源领域样本组成训练数据集训练上述的5种多标记算法,并测试算法在目标领域的预测效果. 算法的5项评价指标随样本数量的变化情况见图 2. 如图所示,随着源领域样本数的增加,BL、 LIFT和S-MLTL的各项指标相对于其它2个算法较稳定; MLTL的多数指标没有明显的变化,但One Error有增大的趋势,这是因为随着样本数量增加,源领域与目标领域特征的分布差异更明显,源领域的特征越来越不适用于目标领域; M-MLTL的Hamming Loss没有明显变化,但其它指标均有不同程度的提升,这说明对源领域知识的学习提高了目标领域的预测效果. 值得注意的是,当训练样本数为500时MLTL算法的各项指标都优于M-MLTL,这是由于本文中的MMD正则项采用的是线性核函数,即采用源域数据集和与目标域数据集的总体均值之差评价分布差异,而小数量样本可能存在选择性偏差(sample selection bias),不能代表整个源领域的分布情况,此时可以将控制参数μ的取值降低以提升算法的分类精度. 当样本数大于1 000时,M-MLTL的各项指标都赶超MLTL. 因此,M-MLTL算法在大样本情况下更有优势.

|
| 图 2 源领域样本数量对分类效果的影响 Figure 2 Influence on the classification results with differentsource domain data number |
低维子空间特征数量和训练样本的个数都会影响算法的计算时间. 实验采用“Corel5k vs ESPGame”数据集,测试不同的潜在子空间特征数和训练样本个数影响下3种降维算法的计算时间.
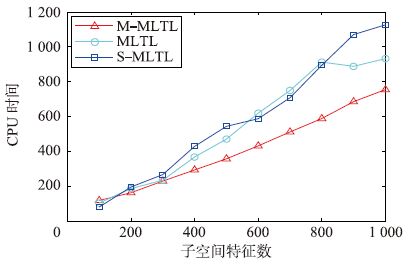
M-MLTL、 MLTL和S-MLTL的计算时间随子空间特征数的变化情况见图 3. 3种算法的计算时间都随子空间特征数增加而增长,其中S-MLTL的计算时间随子空间特征数增加阶梯上涨,MLTL的计算时间变化与S-MLTL类似. 而M-MLTL计算时间与子空间特征数线性相关,这与3.4节的时间复杂度分析相符. 当子空间特征数小于200时S-MLTL和MLTL的计算耗时都小于M-MLTL,但M-MLTL的计算时间随子空间特征数的增加变化相对较小,当子空间特征数大于200时M-MLTL计算时间小于其它两种算法.
|
| 图 3 不同子空间特征数的计算时间 Figure 3 Computational time of different subspace feature number |
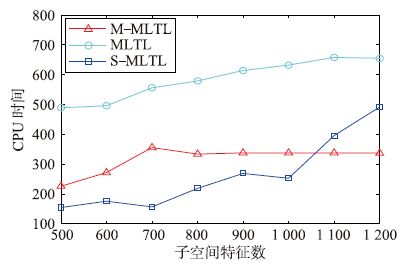
图 4显示了算法计算时间随训练样本增加的变化情况. 由图可知,当样本数量小于700时,3种算法的计算时间都随样本数增加而增长; 但当样本数量大于700时,M-MLTL的计算时间不再受样本数量的影响,而另2种算法的计算时间仍在持续增长,这与3.4节的结论相符,因此本文的算法在大样本学习中计算效率更有优势.
|
| 图 4 不同训练样本数量的计算时间 Figure 4 Computational time ofdifferent training data number |
本文提出了一种新多标记迁移学习算法,通过分解“特征—标记”关系矩阵将源领域样本的标记间关联关系嵌入共享的潜在子空间,同时引入最大均值差异最小化源领域与目标领域在共享子空间中的特征分布差异. 新算法着重解决了多标记迁移学习中共享子空间的领域适应问题. 在多标记图像分类实验中,新算法比目前已有的同类算法有更好的分类效果和较高的计算效率. 同时,新算法关键计算的耗时不受样本数量的影响,因此新算法可以应对大样本的学习问题.
然而当训练样本数量较少时,由于存在选择性偏差,训练样本不能代表整个领域的分布情况,新算法的优势不明显. 如何解决小样本多标记迁移中存在的选择性偏差问题将是下一步的研究方向.
| [1] | 庄福振, 罗平, 何清, 等. 迁移学习研究进展[J]. 软件学报 , 2015, 26 (1) : 26–39. Zhuang F Z, Luo P, He Q, et al. Survey on transfer learning research[J]. Journal of Software , 2015, 26 (1) : 26–39. |
| [2] | Shao L, Zhu F, Li X. Transfer learning for visual categorization: A survey[J]. IEEE Transactions on Neural Networks and Learning Systems , 2014, 26 (5) : 1019–1034. |
| [3] | Jia C, Kong Y, Ding Z, et al. Latent tensor transfer learning for RGB-D action recognition[C]//Proceedings of the ACM International Conference on Multimedia. New York, NJ, USA: ACM, 2014: 87-96. |
| [4] | Perlich C, Dalessandro B, Raeder T, et al. Machine learning for targeted display advertising: Transfer learning in action[J]. Machine Learning , 2014, 95 (1) : 103–127. DOI:10.1007/s10994-013-5375-2 |
| [5] | 许敏, 王士同, 顾鑫. TL-SVM: 一种迁移学习算法[J]. 控制与决策 , 2014, 29 (1) : 141–146. Xu M, Wang S T, Gu X. TL-SVM: A transfer learning algorithm[J]. Control and Decision , 2014, 29 (1) : 141–146. |
| [6] | Zhuang F, Luo P, Xiong H, et al. Exploiting associations between word clusters and document classes for cross-domain text categorization[J]. Statistical Analysis and Data Mining: The ASA Data Science Journal , 2011, 4 (1) : 100–114. DOI:10.1002/sam.v4.1 |
| [7] | Dai W, Xue G R, Yang Q, et al. Co-clustering based classification for out-of-domain documents[C]//Proceedings of the 13th ACM SIGKDD international conference on Knowledge discovery and data mining. New York, NJ, USA: ACM, 2007: 210-219. |
| [8] | 董爱美, 王士同. 共享隐空间迁移SVM[J]. 自动化学报 , 2014, 40 (10) : 2276–2287. Dong A M, Wang S T. A Shared latent subspace transfer learning algorithm using SVM[J]. Acta Automatica Sinica , 2014, 40 (10) : 2276–2287. |
| [9] | 张倩, 李海港, 李明, 等. 基于马尔可夫逻辑网的关联规则迁移学习[J]. 信息与控制 , 2014, 43 (6) : 715–721. Zhang Q, Li H G, Li M, et al. Association rule transfer learning based on Markov logic network[J]. Information and Control , 2014, 43 (6) : 715–721. |
| [10] | Zhou J T, Pan S J, Tsang I W, et al. Hybrid heterogeneous transfer learning through deep learning[C]//Twenty-Eighth AAAI Conference on Artificial Intelligence. Menlo Park, USA: AAAI, 2014: 2213-2219. |
| [11] | Yang P, Gao W. Multi-view discriminant transfer learning[C]//Proceedings of the Twenty-Third international joint conference on Artificial Intelligence. Menlo Park, USA: AAAI, 2013: 1848-1854. |
| [12] | Zhang M L, Zhou Z H. A review on multi-label learning algorithms[J]. IEEE Transactions on Knowledge and Data Engineering , 2014, 26 (8) : 1819–1837. DOI:10.1109/TKDE.2013.39 |
| [13] | Mei S. Predicting plant protein subcellular multi-localization by Chou′s PseAAC formulation based multi-label homolog knowledge transfer learning[J]. Journal of Theoretical Biology , 2012, 310 : 80–87. DOI:10.1016/j.jtbi.2012.06.028 |
| [14] | Tawiah C, Sheng V. Empirical comparison of multi-label classification algorithms[C]//Twenty-Seventh AAAI Conference on Artificial Intelligence. Menlo Park, USA: AAAI, 2013: 1645-1646. |
| [15] | Cheng B, Liu M, Zhang D. Multimodal multi-label transfer learning for early diagnosis of Alzheimer′s disease[M]. Berlin, Germany: Springer-Verlag , 2015 : 238 -245. |
| [16] | Fu Y, Yang Y, Hospedales T, et al. Transductive multi-label zero-shot learning[C]//British Machine Vision Conference. Durham, UK: BMVA Press, 2015. |
| [17] | Han Y, Wu F, Zhuang Y, et al. Multi-label transfer learning with sparse representation[J]. IEEE Transactions on Circuits and Systems for Video Technology , 2010, 20 (8) : 1110–1121. DOI:10.1109/TCSVT.2010.2057015 |
| [18] | Gretton A, Borgwardt K M, Rasch M, et al. A kernel method for the two-sample-problem[C]//Advances in neural information processing systems. New York, NJ, USA: ACM, 2006: 513-520. |
| [19] | Pan S J, Kwok J T, Yang Q. Transfer Learning via Dimensionality Reduction[C]//Twenty-Third Conference on Artificial Intelligence. Menlo Park, USA: AAAI, 2008: 677-682. |
| [20] | Long M, Wang J, Ding G, et al. Adaptation regularization: A general framework for transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering , 2014, 26 (5) : 1076–1089. DOI:10.1109/TKDE.2013.111 |
| [21] | Yang Y, Zha Z J, Gao Y, et al. Exploiting web images for semantic video indexing via robust sample-specific loss[J]. IEEE Transactions on Multimedia , 2014, 16 (6) : 1677–1689. DOI:10.1109/TMM.2014.2323014 |
| [22] | Dumais S T. Latent semantic analysis[J]. Annual review of information science and technology , 2004, 38 (1) : 188–230. |
| [23] | Hestenes M R, Stiefel E. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards , 1952, 49 (6) : 409–436. DOI:10.6028/jres.049.044 |
| [24] | Bartels R H, Stewart G W. Solution of the matrix equation AX+XB=C[J]. Communications of ACM , 1972, 15 (9) : 820–826. DOI:10.1145/361573.361582 |
| [25] | Duygulu P, Barnard K, deFreitas J F G, et al. Object recognition as machine translation: Learning a lexicon for a fixed image vocabulary[M]//Lecture Notes in Computer Science: vol. 2353. Berlin, Germany: Springer-Verlag, 2002: 97-112. |
| [26] | Von Ahn L, Dabbish L. Labeling images with a computer game[C]//Proceedings of the SIGCHI conference on Human factors in computing systems. New York, NJ, USA: ACM, 2004: 319-326. |
| [27] | Guillaumin M, Mensink T, Verbeek J, et al. Tagprop: Discriminative metric learning in nearest neighbor models for image auto-annotation[C]//2009 IEEE 12th International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 2009: 309-316. |
| [28] | Steinwart I. On the influence of the Kernel on the consistency of support vector machines[J]. Journal of Machine Learning Research , 2002, 2 (1) : 67–93. |
| [29] | Elisseeff A, Weston J. A kernel method for multi-labelled classification[C]//Advances in neural information processing systems. Cambridge, Massachusetts, USA: MIT Press, 2001: 681-687. |
| [30] | Zhang M L, Wu L. LIFT: Multi-label learning with label-specific features[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015, 37 (1) : 107–120. DOI:10.1109/TPAMI.2014.2339815 |




