1 引言
21世纪以来,离群点检测(又称为异常检测)作为机器学习领域的重要分支之一,越来越受到人们的关注. 与聚类发现数据集中的多数模式不同,离群点检测通过捕获那些偏离多数模式的异常情况,进而发现似由不同模式产生的,明显不同于其它数据对象的离群点[1]. 目前,离群点检测广泛地运用于传感网络入侵检测、 图像处理、 工业控制系统监控与预警等多个方面,起到监测异常、 预警提示的作用[2-3].
离群点(outlier)可以分为全局离群点、 情境离群点、 集体离群点. 21世纪伊始,由于基于密度的离群点检测算法(local outlier detection algorithm)的提出,又引进了局部离群点的概念[1]. 情境离群点是局部离群点的推广,全局离群点是情境离群点的特例. 由于环境的复杂多变性,在某种情境下,对于整体数据集上正常的数据对象,却可能是当前情境下的离群点,比如某化工仓储企业的所有储罐信息数据,某些数据对象对于整体来说是正常的,但在它对应的局部储罐内,它却是离群点; 甚至在同一个储罐内,由于现场的装卸船作业过程复杂、 持续时间长等原因,数据对象整体平滑,却在局部存在很大波动,即出现局部离群点,及时准确地发现这些离群点对于企业生产来说是至关重要的. 因此在某些情况下,局部离群点的检测要比全局离群点和集体离群点的检测更加灵活、 更有意义.
传统的局部离群点检测算法在处理对象时将对象糅杂在一个特征向量中. 一方面,使用糅杂手段可能导致对象丢失部分本质特征和关键信息,算法无法准确检测离群点; 另一方面,提取后的特征向量需尽可能代表对象,导致向量维度增加,计算复杂度提高. 因此,此类方法对于具有明确、 单一语义的对象可以很好的适用,但面对复杂、 多义的数据集合[4],传统的局部离群点检测算法通过简单的分割和特征提取是无法满足检测要求的.
针对上述问题,本论文提出了一种基于多示例学习(multi-instance learning, MIL)的局部离群点检测算法. 算法采用MIL框架,根据多义对象的各个语义差异提取相应的特征作为示例,并组成多示例包. 然后算法采用退化策略,将原本多示例问题转化为单示例问题,进行计算; 再采用权重调整方法,对不同示例集,根据其自身特点分配不同权重. 最后,结合权重计算综合离群点因子,通过综合离群点因子标记对象是否为局部离群点. 算法已运用在某化工仓储企业的实时监控系统中,并使用企业现场监控数据和公共数据集与LOF算法[5]及其改进算法进行比较,发现所提算法提高了检测的准确性、 全面性和高效性.
2 研究背景 2.1 局部离群点2000年,Breunig等人[5]提出了一种基于密度的局部离群点算法——LOF. 其通过给定的k系数,计算各个对象的局部可达密度,局部离群因子. 该算法最终通过局部离群因子量化对象的离群程度,此算法为局部离群点的经典算法.
自基于密度的局部离群点算法被应用以来,人们对局部离群点检测的理解不断加深. 目前基于LOF的改进算法可以被分为如下两大类:
基于特定数据集上的优化: 2001年,西蒙弗雷泽大学Jin等人[6]针对给定的大数据集,提出了一种仅寻找前n个局部离群点的方法,优化LOF在大数据集中计算量大的缺点. 2002年,Tang等人[7]针对稀疏的、 低密度的数据集,提出了一种计算平均连接距离的新方法,增加了连接路径的计算,用与邻域的平均距离作为离群系数,评估对象的离群程度. 2006年,Chawla等人[8]针对空间维度问题,提出了SLOM(spatial local outlier measure)算法,将数据分割成空间属性、 非空间属性. 2007年,薛安荣等人[9]针对文[8]中的算法,提出了SLOF(spatial local outlier factor)算法,优化SLOM的波动问题. 2014年,周世波等人[10]提出了DBLOD(deviation-based local outlier detection)算法,对数据集进行分区预处理,以块为单位刻画数据对象.
基于算法结构上的优化: 2003年,Papadimitriou等人[11]提出了LOCI(the local correlation integral)算法,自动获取临界值,提高检测效率. 2009年,Gao等人[12]提出一种多粒度局部离群检测(a multi-granularity local outlier detection, MLOD)的方法,减少计算邻域的复杂度. 2010年,Hu等人[13]提出DLOF(a density-based local outlier factor)算法,引入信息熵的概念,在计算对象之间的距离时,采用加权距离提高精度. 2012年,Goldstein[14]提出了FastLOF算法,使用E-M(expectation-maximization)算法,并通过数据集分块来减少LOF中对K邻近距离的计算,但是算法受给定块个数的影响.
2.2 多示例学习1997年,药理学上,针对药物活性预测的研究,Dietterich等人[15]提出了MIL方法. 在MIL中,每个对象被定义为一个训练包(bag),包中包含多个示例(用属性—值对的形式表示),通过对多个包中的多个示例的学习,进行预测. MIL能够应对多义、 复杂的数据对象,保留数据对象的本质,同时经过处理,能够区别每个示例在整个包中的比重,进而获取起关键性作用的示例,为机器学习打开了一个盲区. 因此MIL在国际机器学习界引起了极大的重视. 目前解决MIL问题的方法有很多[16],主要可以分为下面两大类:
基于机器学习方法的优化: 1998年,Wang和Zucker[17]将惰性学习(lazy learning)运用于MIL中. 2002年,Zhou和Zhang[18]将神经网络集成到多示例问题中,提出BP-MIP(BP for multi-instance problems)分类算法. 2003年,Andrews等人[19]将支持向量机(support vector machines, SVM)与MIL结合. 2009年,Zhou等人[20]提出了miGraph算法,将包看作non-i.i.d.例子,通过将包映射到无向图或者构造矩阵的方式获得图核,进行学习.
基于不同数据集合的优化: 2006年,Chen等人[21]通过嵌入式实例选择技术,解决大规模MIL问题. 2014年,Wei等人[22]运用映射的思想优化了多示例学习在大数据集上的可扩展性. 同年,Zhang等人[23]提出了MICS(multi-instance covariate shift)方法,应对在包层和示例层的分布会变化的情况.
现实世界中的对象是具有多义性和复杂性的,一个对象中可能存在多种类型的内在属性和特征. 传统的局部离群点算法往往忽略了这一点,而正是由于MIL是针对这一特性的学习框架,本文将MIL运用于局部离群点检测算法中,提出MIL-LOF算法,以便在离群点的检测上获得更好的效果.
3 MIL-LOF算法目前,局部离群点检测算法通常采用基于密度的离群点检测方法,将数据对象周围的密度与对象领域周围的密度进行比较. 离群点对象周围的密度明显不同于其领域周围的密度. 由于算法模型采用一个特征向量表示一个真实对象,所以对象的多方面属性被糅合在一起,即使出现对真实对象的拆分,也仅是用于确定情境属性或者空间属性[9],未能深入挖掘. 在对象明确、 单一的情况下,算法能够适用. 但如上所述,现实世界中诸如电力、 化工、 能源等企业,数据是复杂多义的[24],对象可以由多种方式进行标记. MIL-LOF算法正是扩展了局部离群点算法对复杂对象集的支持.
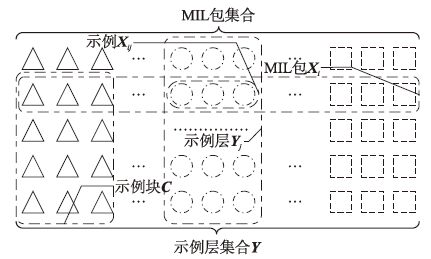
3.1 相关定义定义1 MIL包集合,根据文[15]中定义,给定集合X,∀Xi∈X,称Xi为一个包,包内含有多个示例. 则定义X为MIL包集合. 若Y=XT,则定义Y为其对应的示例层集合.
定义2 示例块,示例块从示例层方面表示MIL包集合的子集,定义其为C={YijYij∈Yj,Yj∈Y}.
上述定义数据集合图形化表述如图 1所示.
定义3 综合局部离群点因子,是度量示例Xi的差异程度的量化,给定∀Xij∈Xi,定义综合局部离群点因子为
|
| 图 1 数据集合剖解图 Figure 1 Anatomy of data collection |
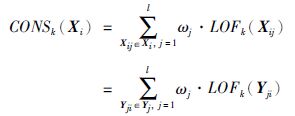
|
(1) |
其中ωj是权重系数W中示例Xij对应的权重. 由行业专家或者缺失权重系数给定,定义缺失权重系数为

|
(2) |
LOFk(Xij)、 LOFk(Yji)来自文[5]中,本文用于表示Xij在C中与其它示例表现的行为的差异程度. 由于C的不同,各Xij对Xi的影响程度也存在差异,所以采用权重机制,从而获得更好的度量效果.
定义4 局部离群点域,给定MIL包集合X中第k个最大差异度为gdiverk,定义局部离群点域为
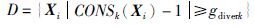
|
(3) |
其中,
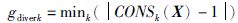
|
(4) |
表示局部离群点的范围空间,域内点即为局部离群点.
3.2 算法思想随着存储技术的高速发展,数据集合愈趋复杂,这给传统的局部离群点检测带来了诸多挑战. MIL自提出以来被用于各类数据挖掘技术中,用于处理复杂的数据集合,诸如,文[24]中用于预测全基因组蛋白质的功能、 文[25]中用于分类与聚类技术. 这类系统中,MIL主要负责数据的拆分与合并过程的处理,与分类与聚类技术耦合性低. 因此,MIL-LOF算法将MIL运用于同样作为数据挖掘一大分支的离群点检测中是完全可行的.
运用MIL技术,数据集合被转化成一个MIL包集合,各个包内含有多个示例. 因此,原先糅杂在一起的对象按照专家设定的语义被有条理地规划到各个示例中,每个对象由一个装有多个示例的包表示,包中的每个示例代表此对象在其特定语义下的解释. 如图 1所示,包完整地、 结构化地保留了对象的整体特征,避免了传统算法提取过程中的丢失. 由定义1可知,通过简单的矩阵转置,转化后的MIL包集合便可转置成示例层集合. 在示例层集合层面上,算法通过计算各示例之间的相对密度确定正例、 反例. 最后,算法通过再次矩阵转置,在MIL包集合层面上,综合计算各包之间的相对度度量,确定局部离群点. MIL-LOF算法采用退化策略[25],通过矩阵转置与分解,将MIL问题退化为传统的单示例问题,将对MIL块的问题转化为对示例块的问题. 不仅有效地解决了在复杂对象集上的问题,提高算法检测的全面性,而且发现,在退化过程中特征向量的维度也随之减少. 由FastLOF算法[13]可知,定义3中LOFk(Xij)的计算性能受维度的影响很大,因此向量维度的减少,使算法复杂度下降.
MIL-LOF算法同时采用了定义4的权重调整策略,专家给定的语义的同时,也给定其所占比重,在缺失情况下,算法采用缺失权重机制. 根据传统MIL定义,如果包内存在至少一个正例,则此包为正包,不包含任何正例,则为反包. MIL-LOF算法优化这一定义,将MIL与LOF结合,通过权重调整策略,将所有正例、 反例都作为判断正包或反包的因子,分配不同权重. 使MIL-LOF算法对真实数据的适应性更强,提高了局部离群点检测的准确性.
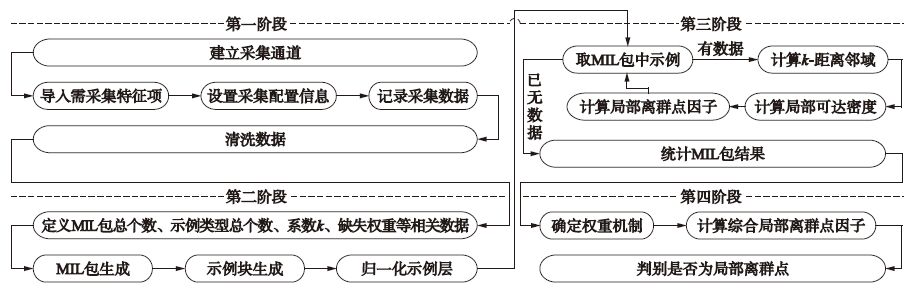
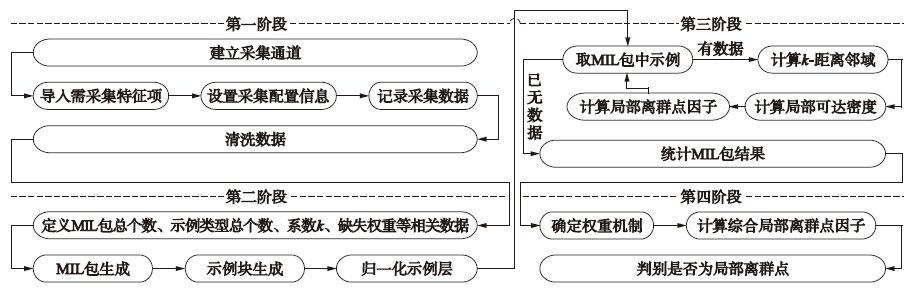
MIL-LOF算法由4个阶段构成. 第一阶段: 预处理,进行数据采集与清洗; 第二阶段: 初始化,根据MIL原理,对数据进行转化处理; 第三阶段: 局部离群点因子计算,根据定义3,对退化后的单示例在其对应示例块中计算局部离群点因子; 第四阶段: 局部离群点检测,根据定义3、 4,计算多示例对象的综合局部离群点因子,确定局部离群点域,标识局部离群点. 具体如图 2所示.
3.3 算法描述算法描述,如表 1所示.
3.4 算法复杂度分析
由上述算法描述可知,MIL-LOF算法是针对多义而又复杂的数据集设计的,其核心为步骤1数据集的结构化过程,通过基于MIL的结构化处理,杂乱的数据集合被组合成一个有序、 全面的MIL包集合. 算法进而使用转置矩阵,转化成示例层集合和示例块,将问题退化到示例层进行运算. 算法的计算复杂度基本由示例数量与维度决定的. 假设,数据集合数目为n, 属性维度为d, 示例层数目m, 领域数为k, 则MIL-LOF算法计算特征之间的距离的平均复杂度为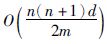

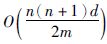

|
| 图 2 算法流程图 Figure 2 Algorithm flowchart |
|
输入: X: 整体MIL包集合 n, l, m: 整体MIL包集合中MIL包总个数、 示例类型总个数、 示例中含特征属性的总个数 W: 缺失权重系数 |
|
1 for ∀Xi∈X do 2 MIL_bag(X),生成MIL包集合; 3 end 4 Y=XT,转化成示例层集合,便于退化策略的计算 5 for ∀Yi∈Y do 6 MIL_block(Y),生成示例块集合; 7 end 8 if(W==null) 9 Init_w(W),初始化缺失权重系数 10 end 11 for ∀Yi∈Y do 12 for ∀Yij∈Yido 13  归一化示例层集合; 归一化示例层集合; 14 end 15 end 16 for ∀Xi∈X do 17 for ∀Yji∈Y,Xi do 18 LOFk(Yji),计算示例块中局部离群因子; 19 end 20 CONSk(Xi),计算综合局部离群点因子; 21 end 22 gdiverk(CONSk(X)),计算最大差异度; 23 Statistics(D),计算局部离群点域,统计离群点. 24 end |
|
输出: CONS: 数据集合的综合局部离群点集合. D: 数据集合中的局部离群点域范围. |
同时,MIL-LOF算法中运用了权重机制如式(3)所示,将所有示例作为判别MIL 包的因子,提高算法全面性、 准确性.
4 MIL-LOF算法的仿真与分析本节利用某化工仓储企业的真实数据集和标准数据集上的采样数据,对MIL-LOF离群点算法的有效性与性能进行分析,并与LOF算法、 DBLOD算法以及KNMOD算法进行比较. 算法仿真运行的硬件环境: CPU为Intel(R) Core(TM) i3-3220 3.30 GHz; 内存为4.00 GB; 操作系统为Windows 7,实验程序用Java、 Python编写,开发环境为JDK1.7、 IDLE(Python GUI).
4.1 工业控制数据集某化工仓储企业的储罐存储的化工原料其价值和危险性都很高,储罐的状态和储量是企业的根本. 目前的工业控制系统只能监控实时数据和对超出阈值的特定项进行报警. 但企业仍然发现储罐的储量会不定期的莫名减少. 如何预防此类事件的发生,并找出储量缺少的原因成为企业的一大难题. 通过调研与分析,此化工仓储企业将MIL-LOF算法集成到工业控制系统中,系统根据专家定义,通过中间采集程序,每两小时采集一次工业控制数据,并记录入数据库. MIL-LOF算法从数据库中获取数据,进行分析,得出异常数据(局部离群点),并生成报表. 通过企业反馈证明算法能够有效地检测出异常数据,为企业减少了损失.
此化工仓储企业拥有70个储罐,采用随机采样的方式,截取在2015年2月1号0点到3月31号12点作为实验数据源,根据专家定义,数据包含设备开关状态、 静态设置特征、 动态实时特征等形式数据,共计49 210项,且都经过现场专门人员审核过,已含有标记位,便于算法的验证. 部分数据如表 2所示.
首先对原始数据进行清洗,集合中49 210项经过第一阶段数据整理与清洗,剩余48 912项. 算法以不同语义作依据,采用MIL技术,将数据结构化为MIL包,比如表 2中第一条1101的数据X1101(深色部分),经过MIL结构化后,此MIL包内装有3个示例,分别对应着设备开关状态语义X11011=(0,1,0)、 静态设置特征X11012=(0.001 2,0.900 6,0,0.909 5)、 动态实时特征X11013=(14.174,6.1,3 757.644,…,-350,4 101.426).
| 特征项 | 1 | 2 | 3 | 4 | … | n-3 | n-2 | n-1 | n |
| 1101 | 14.174 | 6.1 | 3 757.644 | 26.446 | … | 0.001 2 | 0.900 6 | 0 | 0.909 5 |
| 1102 | 18.831 | 4.33 | 5 027.457 | -0.659 | … | 0.000 8 | 0.916 7 | 0 | 0.926 9 |
| 1106 | 16.273 | 4.4 | 4 118.508 | 0 | … | 0.000 8 | 0.917 8 | 0 | 0.927 9 |
| | | | | | | | | | |
| | | | | | | | | | |
| 1204 | 32.767 | 3.26 | 0 | 0 | … | 0.000 8 | 0.874 1 | 0 | 0.879 2 |
| 1206 | 9.513 | 16.23 | 2 428.385 | -108.068 | … | 0.001 1 | 0.791 6 | 10 | 0.798 7 |
| 1207 | 2.705 | 23.29 | 712.641 7 | -90.039 | … | 0.001 1 | 0.879 | 0 | 0.875 2 |
| 1208 | 8.049 | 3.71 | 1 875.34 | 0.063 | … | 0.000 9 | 0.791 3 | 0 | 0.798 6 |
由于仿真环境的限制和不同储罐存储的物料及其本身材质等的差异性,仿真实验在70个储罐中随机抽取1个储罐作为检测对象集合. 取出随机抽样中的一个储罐——1310号储罐,其存储的为冰醋酸,材质为316l(不锈钢),其对象集合数703项,共20个离群点,根据Goldstein[14]的分析,设置系数k为集合数的平方根26. 运用MIL-LOF算法以及LOF算法、 DBLOD算法、 KNMOD算法进行检测,结果如图 3所示.
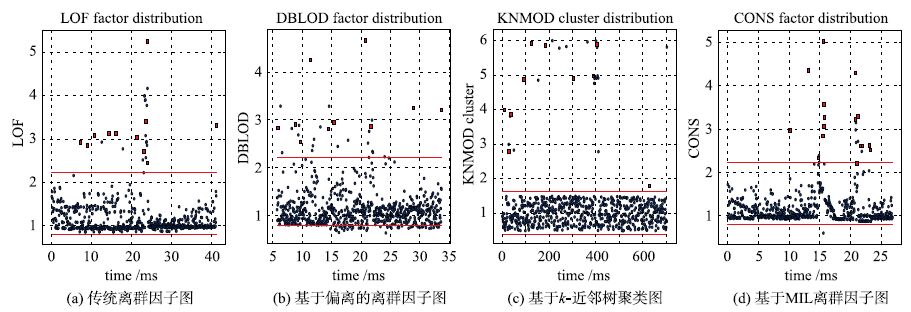
|
| 图 3 工业控制数据集中离群点因子分布图 Figure 3 Distribution of outlier factor in industrial data set |
根据定义8,图中红色直线为离群点因子分割线,其内部为正常数据,其外部为局部离群点域. 图 3(a),局部离群点域中检测正确为11个(红色方块标出),共用时40.822 4 ms; 图 3(b),局部离群点域中检测正确为10个,共用时34.085 6 ms; 图 3(c),局部离群点域中检测正确为10个,共用时29.482 2 ms. 图 3(d),局部离群点域中检测正确为18个,共用时26.781 3 ms. 实验发现,在特定的工业数据集上,MIL-LOF算法在精确度和效率上都呈现出了良好的结果.
4.2 KDD CUP99数据集为了证明算法的可推广性和使用性,算法选用KDD CUP99数据集进行了对比实验,KDD CUP99是在1999年举行KDD竞赛时采用的数据集,来自1998年美国国防部高级规划署(DARPA)在MIT林肯实验室进行了一项入侵检测评估项目. 项目收集了9周时间的TCPdump网络连接和系统审计数据,仿真各种用户类型、 各种不同的网络流量和攻击手段. 数据集包含500万条记录,每条记录含42个属性,其中41个为特征属性和1个标签属性,其中41个特征属性又被分为4大类. 为了构造适用于离群点检测的数据集,需要对数据集进行分类和提取,并确定多义对象的拆分依据. 为了简化实验,论文使用特征属性的类型作为MIL的拆分依据.
仿真系统首先按照记录的不同标签属性,将记录分别存入不同的文件中,然后系统采用随机抽样的方式分别从正常数据文件中,提取5 000作为测试数据集D1,最后同样采用随机抽样的方式从各攻击类型的文件中抽取若干数量的攻击数据,共计50条,附加到测试数据集中. 将检测结果与实际标签作对比,计算检测的准确度.
如图 4(a)所示,局部离群点域中检测正确为18个(红色方块标出),共用时261.143 ms; 图 4(b),局部离群点域中检测正确为31个,共用时157.125 ms; 图 4(c),局部离群点域中检测正确为33个,共用时177.045 ms; 图 4(d),局部离群点域中检测正确为37个,共用时133.62 ms. 实验发现,在KDD CUP99数据集上,MIL-LOF算法在精确度和效率上都呈现出了良好的结果.
|
| 图 4 KDD CUP99数据集中离群点因子分布图 Figure 4 Distribution of outlier factor in KDD CUP99 data set |

|
| 图 5 ROC曲线 Figure 5 Receiver operator characteristic curves |
为了检测算法性能,论文采用受试者工作特征曲线(receiver operator characteristic curve, ROC)比较不同算法. 如图 5,横坐标表示假阳性率(1-特异度),纵坐标表示真阳性率(灵敏度). 图 5(a)、5(b)显示在KDD CUP99数据集上,各算法的ROC曲线和AUC(area under ROC curve)值,优化的算法性能均高于传统算法,其中MIL-LOF较好. 由于LOF、 DBLOD、 KNMOD算法都针对局部数据块分析,其中DBLOD采用先分区(聚类),再单独计算偏离度; KNMOD采用先计算相似性,再分割最小生成树. 以上算法都忽略了独立数据的多义性差异,以及其影响. MIL-LOF算法充分考虑数据的复杂性,并运用数据的自身特性,挖掘其更深层次的区别. 如5图(c)、 5(d)的ROC曲线所示,在工业控制数据集上,MIL-LOF的AUC明显高于其他算法.
5 结论通过局部离群点检测,机器学习帮助人们解决了许多难题,越来越受到学者和企业的重视,论文提出一种基于多示例学习的局部离群点检测算法扩展了局部离群点检测的应用领域,弥补了其在真实世界中,针对多义数据的不足,同时提高了算法的效率与准确度. 然而,随着数据量和数据复杂度的不断提升,MIL-LOF算法也存在诸多不足,例如,如何动态的结构化,减少人工的干预; MIL中如何进一步优化退化策略; 在MIL包中,如何动态发现对结果影响较大的示例,分析原因或者动态调整其权重等等,这些都是下一步研究的内容.
| [1] | Han J W, Kamber M. Data mining: Concepts and techniques[M]. New York: Morgan Kaufmann Publishers , 2001 . |
| [2] | Bossers H C M, Hurink J L, Smit G J M. Selection of tests for outlier detection[C]//the IEEE 31st VLSI Test Symposium. Piscataway, NJ, USA: IEEE, 2013: 1-6. |
| [3] | Chiu A L, Fu A W. Enhancements on local outlier detection[C]//International Database Engineering and Applications Symposium. Piscataway, NJ, USA: IEEE, 2003: 298-307. |
| [4] | Zhou Z H, Zhang M L, Huang S J, et al. Multi-instance multi-label learning[J]. Artificial Intelligence , 2012, 176 (1) : 2291–2320. DOI:10.1016/j.artint.2011.10.002 |
| [5] | Breunig M, Kriegel H, Ng R, et al. LOF: Identifying density-based local outliers[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data. New York, NY, USA: ACM, 2000: 93-104. |
| [6] | Jin W, Tung A K H, Han J W. Mining top-nlocaloutliers in large databases[C]//Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: ACM, 2001: 293-298. |
| [7] | Tang J, Chen Z, Fu A, et al. Enhancing effectiveness of outlier detections for low density patterns[C]//6th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin, Germany: Springer-Verlag, 2002: 535-548. |
| [8] | Chawla S, Sun P. SLOM: A new measure for local spatial outliers[J]. Knowledge and Information Systems , 2006, 9 (4) : 412–429. DOI:10.1007/s10115-005-0200-2 |
| [9] | 薛安荣, 鞠时光, 何伟华, 等. 局部离群点挖掘算法研究[J]. 计算机学报 , 2007, 30 (8) : 1455–1463. Xue A R, Ju S G, He W H, et al. Study on algorithms for local outlier detection[J]. Chinese journal of computers , 2007, 30 (8) : 1455–1463. |
| [10] | 周世波, 徐维祥. 一种基于偏离的局部离群点检测算法[J]. 仪器仪表学报 , 2014, 35 (10) : 2293–2297. Zhou S B, Xu W X. Deviation-based local outlier detection algorithm[J]. Chinese Journal of Scientific Instrument , 2014, 35 (10) : 2293–2297. |
| [11] | Papadimitriou S, Kitagawa H, Gibbons P B, et al. LOCI: Fast outlier detection using the local correlation integral[C]//19th International Conference on Data Engineering. Piscataway, NJ, USA: IEEE, 2003: 315-326. |
| [12] | Gao L, Yu S Y, Luo Y P, et al. MLOD: Multi-granularity local outlier detection[C]//IEEE International Conference on Granular Computing. Piscataway, NJ, USA: IEEE, 2009: 171-175. |
| [13] | Hu C P, Qin X L. A density-based local outlier detecting algorithm[J]. Journal of Computer Research & Development , 2010, 47 (12) : 2110–2116. |
| [14] | Goldstein M. FastLOF: An expectation-maximization based local outlier detection algorithm[C]//21st International Conference on Pattern Recognition (ICPR). Piscataway, NJ, USA: IEEE, 2012: 2282-2285. |
| [15] | Dietterich T G, Lathrop R H. Solving the multiple-instance problem with axis-parallel rectangles[J]. Artificial Intelligence , 1997, 89 (1/2) : 31–71. |
| [16] | Amores J. Multiple instance classification: Review, taxonomy and comparative study[J]. Artificial Intelligence , 2013 (1) : 81–105. |
| [17] | Wang J, Zucker J D. Solving the multiple-instance problem: A lazy learning approach[C]//17th International Conference on Machine Learning. San Francisco, CA, USA: Morgan Kaufmann, 2000: 1119-1126. |
| [18] | Zhou Z H, Zhang M L. Neural networks for multi-instance learning[R]. Nanjing: Nanjing University, 2002. |
| [19] | Andrews S, Tsochantaridis I, Hofmann T. Support vector machines for multiple-instance learning[C]//Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2003: 561-568. |
| [20] | Zhou Z H, Sun Y Y, Li Y F. Multi-instance learning by treating instances as non-i.i.d. samples[C]//26th International Conference on Machine Learning (ICML′09). New York, USA: ACM, 2009: 1249-1256. |
| [21] | Chen Y X, Bi J B, Wang J Z. MILES: Multiple-instance learning via embedded instance selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2006 : 1931–1947. |
| [22] | Wei X S, Wu J, Zhou Z H. Scalable multi-instance learning[C]//14th IEEE International Conference on Data Mining (ICDM′14). Piscataway, NJ, USA: IEEE, 2014: 1037-1042. |
| [23] | Zhang W J, Zhou Z H. Multi-instance learning with distribution change[C]//28th AAAI Conference on Artificial Intelligence (AAAI′14). San Francisco, CA, USA: AAAI, 2014: 2184-2190. |
| [24] | Wu J S, Huang S J, Zhou Z H. Genome-wide protein function prediction through multi-instance multi-label learning[J]. ACM/IEEE Transactions on Computational Biology and Bioinformatics , 2014, 11 (5) : 891–902. DOI:10.1109/TCBB.2014.2323058 |
| [25] | Zhou Z H, Zhang M L, Huang S J, et al. Multi-instance multi-label learning[J]. Artificial Intelligence , 2012, 176 (1) : 2291–2320. DOI:10.1016/j.artint.2011.10.002 |
| [26] | 雷小锋, 谢昆青, 林帆, 等. 一种基于K-Means局部最优性的高效聚类算法[J]. 软件学报 , 2008, 19 (7) : 1683–1692. DOI:10.3724/SP.J.1001.2008.01683 Lei X F, Xie K Q, Lin F, et al. An efficient clustering algorithm based on local optimality of K-means[J]. Journal of software , 2008, 19 (7) : 1683–1692. DOI:10.3724/SP.J.1001.2008.01683 |
| [27] | Zhu Q, Fan X, Feng J. Outlier detection based on k-neighborhood MST[C]//2014 IEEE International Conference on Information Reuse and Integration (IRI). Piscataway, NJ, USA: IEEE, 2014: 718-724. |



