1 引言
水下滑翔机是一种依靠浮力驱动的新型自主水下机器人,具有低成本、 长续航力等优点,适合于大范围海洋环境观测[1-3]. 现阶段,一些水下滑翔机已经发展的相当成熟,实现了商业化,如Webb公司生产的Slocum[4]、 华盛顿大学研制的Seaglider[5]和Scripps海洋研究所研制的Spray[6]; 还有一些水下滑翔机现阶段仍处在工程应用阶段,如中国科学院沈阳自动化研究所的SeaWing水下滑翔机[7-9].
深平均流是指不同深度水平方向上海流的平均值,其反映了滑翔机航行区域内海水局部流动情况. Merckelbach给出了水下滑翔机深平均流估算的基本原理[10],将水下滑翔机实际出水位置与静水中船位推算预测位置的矢量差除以滑翔周期时间即可得到该行驶周期的深平均流[10-11]. Smith等利用无迹卡尔曼滤波给出了静水中滑翔机航位推算的不确定性,在此基础上进行深平均流估算[12]. Rusello和Ellis用装载在水下滑翔机上的流速剖面仪来改善水下滑翔机水下船位推算的精度,并近一步进行了深平均流计算[13-14]. 在工程上,深平均流最基本的应用是直接用于指导下一周期水下滑翔机的航向,较精确的深平均流可以提高滑翔机定位、 跟踪及规划的精度. 深平均流还有一些其它的应用,如Dobson利用水下滑翔机得到的深平均流数据来与两个不同的海洋模型预测得到的海流数据进行比较,以确认海洋模型预测的有效性[15]. Kim使用滑翔机实时获取的深平均流数据来修正了安装在滑翔机上加速计的误差[16]. Schaeffer等将水下滑翔机获取的深平均流对高频雷达测得的海流数据进行了验证[17].
在深平均流估算中,一般将GPS(global positioning system)定位误差忽略,而认为对其精准度造成影响的部分仅为水下滑翔机船位推算. 滑翔机水平方向速度对船位推算的精度会产生很大影响,但是很难精确求出水平方向速度,因为滑翔机并不携带测速仪,同时耐压舱压缩变形和海水密度差异都将引起驱动净浮力发生变化,从而造成水下滑翔机运动速度发生变化,并且滑翔机在行驶过程中会存在很大的一段非稳定区间. 文[18]提出了一种较为有效的计算滑翔机水平速度的方法,但是其每次计算均需要相应剖面的三维电子罗盘(TCM)数据和CTD(conductance, temperature, depth)数据,并且计算极为耗时,这在实际应用上会带来很大的不方便. 如何快速地得到较为精确的水下滑翔机的水平方向速度是一个水下滑翔机在行驶中所面临的实际问题.
本文首先介绍了深平均流估算方法. 然后,给出了两种水下滑翔机水平方向速度计算模型: 一种为文[18]所提出的水平方向速度求取模型; 另一种为考虑滑翔机耐压舱压缩和海水密度差异产生额外的净浮力,结合水下滑翔机运动模型而建立的水下滑翔机水平方向速度快速计算模型. 结合3台水下滑翔机海试数据,对这2种速度模型进行比较. 最后,利用快速计算模型得到的速度估计了深平均流,并分析了深平均流的有效性.
2 深平均流估算方法当水下滑翔机从某点Pn开始下潜,经过一个滑翔周期后从Pn+1点浮出,滑翔机实际出水位置Pn+1可以由GPS读出. 假设水下滑翔机运动速度已知,通过船位推算可以获得在静水环境下滑翔机从Pn点经过一个滑翔周期后到达的位置Pn+1,0. 设一个滑翔周期时间为Tn,则该位置环境深平均流为真实出水位置与推算出水位置的矢量差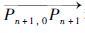

|
(1) |
其中计算Pn+1,0的位置需要用到水下航位推算,其与Pn满足关系:
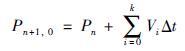
|
(2) |
其中,Δt为导航系统的采样周期,满足条件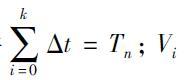
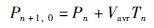
|
(3) |
出于成本考虑,很少有水下滑翔机携带测速装置. 其在海洋中按锯齿状直线运动行驶,真实运动速度会受到多种因素影响: 首先,耐压舱压缩变形和海水密度差异将引起驱动净浮力发生变化,会进一步导致速度不断发生改变; 其次,水下滑翔机剖面周期中存在较长的一段非稳定区间. 这些因素导致精确确定水下滑翔机的水平方向速度较为困难. 下面给出两种水下滑翔机水平方向速度的求取方案.
3.1 基于实时TCM、 CTD数据的水平方向速度模型文[18]提到,水下滑翔机水平方向速度可以利用深度传感器及姿态传感器的数据来求取,其方式如下:
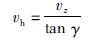
|
(4) |
式中,vz是水下滑翔机深度的差分,γ为滑翔角,vh为水下滑翔机水平方向速度. γ为俯仰角θ和攻角α之差:
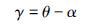
|
(5) |
攻角的表达方式为
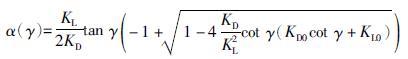
|
(6) |
式中,KL0、 KL、 KD0、 KD分别为水下滑翔机的升力和阻力系数. 当滑翔机结构确定后,这些系数都是常数. 式(4)中所求取的水平方向速度为滑翔机CTD传感器每个采样周期内的值,如果CTD传感器周期为N,则平均后的水平方向速度为
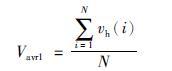
|
(7) |
很显然,这种计算滑翔机水平方向速度的模型需要每个剖面的TCM和CTD数据. 一般说来,水下滑翔机在每个滑翔周期行驶完毕后,会通过GPS以及铱星通讯装置与岸基实时传输这些数据,所需通讯费用较高. 另外,因为海况原因,有时会发生传输失败的情形.
3.2 水平方向速度快速计算模型本部分给出另外一种水下滑翔机水平方向速度的快速求取模型. 其考虑了耐压舱压缩变形、 海水密度差异,非稳定行驶区间等因素. 下面对此进行说明.
对于同一台滑翔机,在给定驱动控制率调节下,其非稳定区间所占的深度范围基本一致,如果设定下潜深度为hmax,则其非稳定区间为[0,h1]和[hmax-Δh,hmax],稳定区间为[h1,hmax-Δh],其中[hmax-Δh,hmax]极小,予以忽略.
在稳定区间内,水下滑翔机进行直线锯齿状稳定运动. 根据水下滑翔机稳态运动特性,其速度可表示为[19]
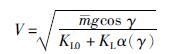
|
(8) |
其中g=9.8 m/s2为重力加速度,为滑翔机所受到的驱动净浮力.
一般认为水下滑翔机的驱动净浮力仅为油囊输出浮力mb. 实际上,当水下滑翔机在海水中运行时,因耐压舱压缩和海水密度差异影响也可导致舱体部分产生净浮力,设这部分附加净浮力为madd(h). 附加净浮力为滑翔机下潜深度h的函数. 滑翔机的总净浮力m(h),即为mb和madd(h)这两部分之和:
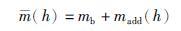
|
(9) |
水下滑翔机在投入水中航行前需要进行配平,设配平密度ρbalance. 在此密度下滑翔机的浮力(油囊提供的驱动浮力为0)和重力相等. 假设油囊体积改变±VB,则油囊提供的净浮力为
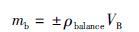
|
(10) |
设滑翔机重力为m,中性体积为Vglider0,则:
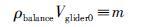
|
(11) |
假定在深度h处,滑翔机舱体的压缩量为ΔV(h),则在此深度下水下滑翔机的体积为
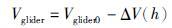
|
(12) |
一般认为,舱体压缩量和深度成正比关系,即可以用κh来表示ΔV(h),于是深度h处的滑翔机体积为

|
(13) |
其中系数κ的单位为L/m.
假定深度h处的海水密度为ρ(h),则在该深度处因海水密度和舱体压缩导致的舱体部分净浮力为
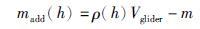
|
(14) |
海水密度ρ(h)主要是由海水的温度、 盐度和压力决定,可以通过CTD传感器测量海水的温度、 盐度和深度来计算获取. 对于从时间和空间上跨度较小的海域,认为海水密度随深度变化规律基本一致. 因此,可以采用拟合公式来获得近似的海水密度表达式.
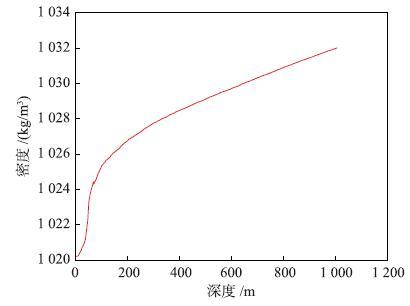
按照常用的EOS-80方程[20],基于CTD测量数据可以得到不同深度下海水密度(如图 1所示),采用多项式对其进行拟合:
|
| 图 1 海水密度垂直剖面 Figure 1 Seawater density in a vertical profile |
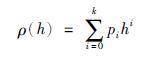
|
(15) |
水下滑翔机在稳定运动滑翔区间,因海水密度差异和舱体压缩导致的附加驱动净浮力为
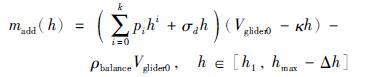
|
(16) |
附加驱动浮力随着深度变化而不断变化. 由式(8)可知,速度也将随深度而不断变化. 为了降低计算量,需要对水下滑翔机运动速度计算进行简化. 将稳定区间内的速度平均化为
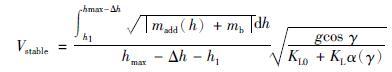
|
(17) |
其中,h1、 hmax-Δh是稳定区间的上下限.
除了稳定滑翔运动区间外,水下滑翔机滑翔周期中还存在一段非平稳区间[0,h1]. 对于非稳定区间,平均运动速度可以近似为稳态区间平均速度的一半,即0.5Vstable.
将所得速度取水平方向分量,则水下滑翔机一个滑翔机周期内的水平运动速度为
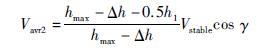
|
(18) |
在本部分首先比较两种速度模型求出的水平方向速度Vavr1与Vavr2,然后再将Vavr2用于求取深平均流并验证其有效性. 取3台不同滑翔机的海试数据进行测试,水下滑翔机相同特征参数为: KL0=0.12,KL=-448.37,KD0=-5.72,KD=-401.49,Vglider0=63.75 L; 耐压舱压缩率系数κ=0.000 268 L/m; Δh=10 m. 3台滑翔机的不同参数列于表 1.
| 名称 | hmax/m | 剖面个数 | h1/m | ρbalance/(kg/m3) | θ/(°) | mb/kg |
| 1000J002 | 1 000 | 30 | 90 | 1 023 | 35,30 | 0.5 |
| 1000J003 | 800 | 21 | 90 | 1 024.5 | 20 | 0.3 |
| 300K002 | 300 | 30 | 45 | 1 023 | 20 | 0.5 |
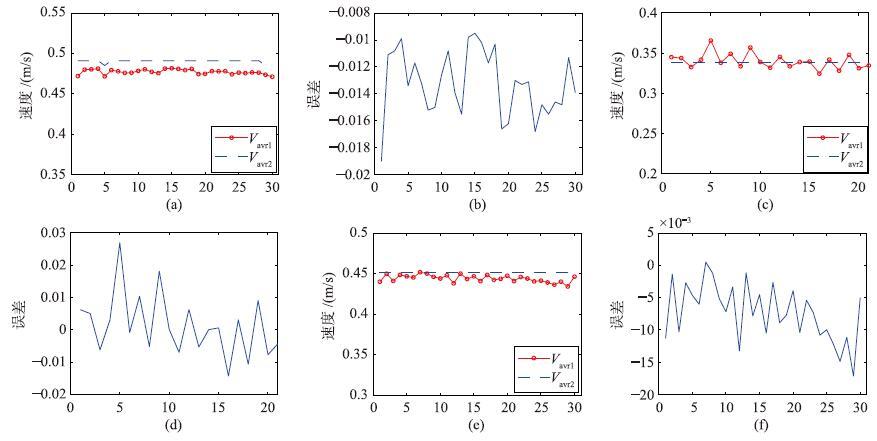
图 2给出了3台滑翔机两种速度模型输出速度的比较及误差,其中1000J002的速度及误差对应图 2(a)和图 2(b),1000J003的速度及误差对应图 2(c)和图 2(d),300K002的速度及误差对应图 2(e)和图 2(f). 表 2为这两种速度模型各自求取一周期速度所需平均CPU耗时.
|
| 图 2 3台水下滑翔机在两种速度计算模型下的速度及其误差 Figure 2 The speeds and errors using two different speed calculation modes of the three gliders |
| 名称 | Time_CPU1/s | Time_CPU2/s |
| 1000J002 | 71.38 | 0.094 |
| 1000J003 | 123.04 | 0.095 |
| 300K002 | 39.81 | 0.094 |
由图 2看出,按第1种速度模型得到的速度Vavr1与第2种速度模型得到的速度Vavr2相差不大,误差一般能够控制在±0.02 m/s以内. 由表 2可以看到,求取Vavr1的时间远多于求取Vavr2的时间. 考虑到水下滑翔机在海上行驶时计算速度的实时性要求,海况及设备造成的通讯问题可能导致TCM和CTD实时数据无法及时传送,故第2种速度模型求得速度的优越性显而易见.
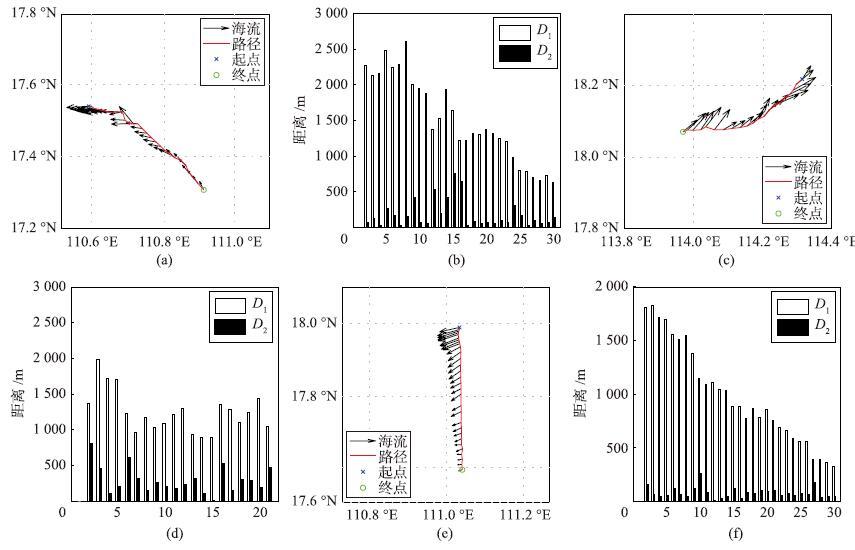
4.2 深平均流验证将3台水下滑翔机1000J002、 1000J003和300K002所求得的Vavr2代入式(3)和式(1),即可得到滑翔机的深平均流,如图 3(a)、 图 3(c)、 图 3(e)所示,其中用蓝色“×”和绿色“”表示每台滑翔机行驶的起点和终点,红色曲线表示每台滑翔机的行驶路线,黑色箭头表示各周期的深平均流.
|
| 图 3 3台水下滑翔机的深平均流及其有效性验证 Figure 3 Depth average currents and the effectiveness tests of the three gliders |
为了验证深平均流估算的正确性,将上一滑翔周期估算的深平均流看下一滑翔周期的深平均流,并将其与下一滑翔周期速度进行矢量求和,于是可以得到基于深平均流估计的下一滑翔周期出水点位置. 将考虑深平均流因素预测的出水点位置、 不考虑深平均流因素预测的出水点位置分别与下一滑翔周期真实出水点位置比较,即可验证深平均流估算的有效性. 先求不含流的出水点预测位置与真实位置的距离,设其为D1,再求含深平均流的出水点预测位置与真实位置的距离,设其为D2. 将D1与D2作成直方图,如图 3(b)、3(d)、 3(f)所示,可以看到对于所有滑翔机的所有周期,考虑深平均流的滑翔机出水点位置预测精度高于不考虑深平均流的滑翔机出水位置预测精度.
5 结论深平均流对水下滑翔机航行路径规划具有重要作用,精确的深平均流可以更好地辅助滑翔机定位与路径规划. 本文研究了滑翔机舱体压缩和海水密度差异对速度的影响,结合滑翔机运动过程给出了一种水下滑翔机水平速度快速计算模型,基于3台水下滑翔机海试数据,将该模型与另外一种较耗时且需要实时传感器数据的水平速度计算模型进行比较,其优越性较为明显. 最后将速度快速计算模型用于深平均流估计,基于该深平均流估算方法,分别计算了这3台水下滑翔机试验海区的深平均流信息,利用获得的深平均流信息可以有效提高水下滑翔机出水位置的预测精度.
| [1] | Leonard N E, Paley D A, Davis R E, et al. Coordinated control of an underwater glider fleet in an adaptive ocean sampling field experiment in Monterey Bay[J]. Journal of Field Robotics , 2010, 27 (6) : 718–740. DOI:10.1002/rob.v27:6 |
| [2] | Fiorelli E, Bhatta P, Leonard N E, et al. Adaptive sampling using feedback control of an autonomous underwater glider fleet[C]//Proceedings of 13th International Symposium on Unmanned Untethered Submersible Technology (UUST), 2003: 1-16. |
| [3] | Bhatta P, Fiorelli E, Lekien F, et al. Coordination of an underwater glider fleet for adaptive sampling[C]//Proceedings of International Workshop on Underwater Robotics. 2005: 61-69. |
| [4] | Sherman J, Davis R E, Owens W B, et al. The autonomous underwater glider "Spray"[J]. IEEE Journal of Oceanic Engineering , 2001, 26 (4) : 437–446. DOI:10.1109/48.972076 |
| [5] | Webb D C, Simonetti P J, Jones C P. SLOCUM: An underwater glider propelled by environmental energy[J]. IEEE Journal of Oceanic Engineering , 2001, 26 (4) : 447–452. DOI:10.1109/48.972077 |
| [6] | Eriksen C C, Osse T J, Light R D, et al. Seaglider: A long-range autonomous underwater vehicle for oceanographic research[J]. IEEE Journal of Oceanic Engineering , 2001, 26 (4) : 424–436. DOI:10.1109/48.972073 |
| [7] | Zhang S, Yu J, Zhang A, et al. Spiraling motion of underwater gliders: Modeling,analysis,and experimental results[J]. Ocean Engineering , 2013, 60 (3) : 1–13. |
| [8] | Huang Y, Yu J, Zhao W, et al. A practical path tracking method for autonomous underwater gilders using iterative algorithm[C]//OCEANS'15 MTS/IEEE Washington. Piscataway, NJ, USA: IEEE, 2015: 1-6. |
| [9] | Yu J, Zhang F, Zhang A, et al. Motion parameter optimization and sensor scheduling for the sea-wing underwater glider[J]. IEEE Journal of Oceanic Engineering , 2013, 38 (2) : 243–254. DOI:10.1109/JOE.2012.2227551 |
| [10] | Merckelbach L M, Briggs R D, Smeed D A, et al. Current measurements from autonomous underwater gliders[C]//9th IEEE/OES Working Conference on Current Measurement Technology. Piscataway, NJ, USA: IEEE, 2008: 61-67. |
| [11] | Chang D, Zhang F, Edwards C R. Real-time guidance of underwater gliders assisted by predictive ocean models[J]. Journal of Atmospheric and Oceanic Technology , 2015, 32 (3) : 562–578. DOI:10.1175/JTECH-D-14-00098.1 |
| [12] | Smith R N, Kelly J, Chao Y, et al. Towards the improvement of autonomous glider navigational accuracy through the use of regional ocean models[C]//ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. New York, NY, USA: ASME, 2010: 597-606. |
| [13] | Ellis D, Washburn L, Ohlmann C, et al. Improved methods to calculate depth-resolved velocities from glider-mounted ADCPs[C]//Current, Waves and Turbulence Measurement (CWTM), 2015 IEEE/OES Eleventh. Piscataway, NJ, USA: IEEE, 2015: 1-10. |
| [14] | Rusello P J, Yahnker C, Morris M. Improving depth averaged velocity measurements from seaglider with an advanced acoustic current profiler, the nortek ad2cp-glider[C]//Oceans 2012. Piscataway, NJ, USA: IEEE, 2012: 1-8. |
| [15] | Dobson C, Mart J, Strandskov N, et al. The challenger glider mission: A global ocean predictive skill experiment[C]//Oceans 2013. Piscataway, NJ, USA: IEEE, 2013: 1-8. |
| [16] | Kim J, Park Y, Lee S, et al. Underwater glider navigation error compensation using sea current data[C]//Proceedings of the 19th IFAC World Congress. Laxenburg, Austria: IFAC, 2014: 9661-9666. |
| [17] | Schaeffer A, Roughan M. Influence of a western boundary current on shelf dynamics and upwelling from repeat glider deployments[J]. Geophysical Research Letters , 2015, 42 (1) : 121–128. DOI:10.1002/2014GL062260 |
| [18] | Claus B, Bachmayer R. Terrain-aided navigation for an underwater glider[J]. Journal of Field Robotics , 2015, 32 (7) : 935–951. DOI:10.1002/rob.2015.32.issue-7 |
| [19] | 朱心科, 俞建成, 王晓辉. 能耗最优的水下滑翔机采样路径规划[J]. 机器人 , 2011, 33 (3) : 360–365. DOI:10.3724/SP.J.1218.2011.00360 Zhu X K, Yu J C, Wang X H. Sampling path planning of underwater glider for energy consumption[J]. Robot , 2011, 33 (3) : 360–365. DOI:10.3724/SP.J.1218.2011.00360 |
| [20] | Fofonoff N P. Physical properties of seawater: A new salinity scale and equation of state for seawater[J]. Journal of Geophysical Research: Oceans , 1985, 90 (C2) : 3332–3342. DOI:10.1029/JC090iC02p03332 |



