1 引言
目前,大中城市普遍存在交通拥堵,这已成为城市经济与社会发展的瓶颈之一. 当前,交通信号控制仍为控制网络内车流及保证交通安全的有效管理手段. 同时,科学技术的快速发展也允许将新的控制理论方法和技术手段引入交通控制领域来解决交通问题[1]. 因此,不同的网络建模与控制方法已被提出,如最优控制方法[2-4]、 模型预测控制方法[5]、 混杂系统建模与控制方法[6-12]、 智能控制方法[13]等.
网络典型场景是: 网络内某些路段拥堵产生车辆排队滞留、 溢流等现象,而其它路段内仍有空间未被充分利用,即网络内车流分布不均衡. 因此,网络均衡为交通控制系统合理控制目标,缓解网络局部拥堵具有实际应用价值. 通常,交通控制系统的优化以路口延误或旅行时间等为性能指标,通过在线或离线优化方法求解最优信号控制方案,如文[4-6, 13]中工作,而均衡性未体现在性能指标中. 文[7, 9-12]提出路口稳态信号控制方法,思想为: 求解路口信号控制策略,使得车辆排队达到期望状态. 若路口期望状态表示路口状态的某种均衡,则稳态信号控制可实现路口某一状态的均衡. 文[7]以路口延误为性能指标,采用离线优化求解达到期望状态的最优信号灯切换时刻. 文[9-11]采用车流清空及其扩展的信号绿时反馈控制策略,使得车辆排队收敛于交通控制中最短信号周期所对应的周期车辆排队,可实现路口各相位饱和度的均衡,信号控制策略需满足非饱和交通条件. 文[12]采用鲁棒控制方法求解绿时反馈控制策略. 文[2-3]采用“存储—转发”(store-and-forward)模型对网络交通流演化建模,应用线性二次最优控制理论提出TUC(traffic-responsive urban control)信号绿时状态反馈控制策略. TUC策略为集中式在线反馈信号控制策略,网络均衡性体现在性能指标中. TUC策略已经过充分验证[14-15],尤其适用于过饱和网络控制. 在TUC策略基础上,文[8]以单个路口为单元,提出网络混杂控制策略. TUC策略性能指标中包含网络均衡性,但未考虑网络内路段动/静态特征的差异性,并且TUC策略的执行需要网络稳态信息,一般而言,网络稳态(期望状态)不易确定.
近20年间,多智能体系统(multi-agent systems, MASs)分布式协作控制由于其广泛的应用吸引了来自于不同学科学者的关注,已成为控制理论前沿研究方向之一,为交通信号控制提供了新的发展空间. 众多MASs协作控制问题可归结为一致性控制问题,MASs一致性含义为通过信息共享与交互,所有智能体的信息状态渐近趋向于同一状态值. 关于MASs一致性已有丰富的理论与应用研究成果[16]. 相比于系统一致性,系统分群一致具有一般性,含义为[17]: 智能体划分为有限子集,子集内智能体可达状态一致,不同子集一致稳态值可不同. 若交通网络状态可达一致或分群一致,即可实现网络某种状态均衡. 因此,交通信号控制为一致性理论成果开辟了新的应用领域. 一致与分群一致控制思想在交通控制领域已有初步应用. 文[18]将一致性引入交通控制,应用部分变量稳定性理论提出一致性信号绿时状态反馈控制设计方法,信号控制为集中式. 文[19-20]将网络内路段视为智能体,将分群一致引入交通信号控制,提出分群一致性信号绿时状态反馈控制设计方法,信号控制为分布式. 相比于文[18]中结果,文[19-20]将路段集合进行划分,每个子集内路段交通状态收敛于一致稳态值,不同子集一致稳态值可不同,可描述网络内路段动态/静态特征的差异性. 文[19-20]中考虑的网络控制结构较为特殊,各路口具有两相位设置,并且信号控制律不能保证系统交通状态的非负性演化.
交通系统具有一个明显特征,即交通状态的非负性. 初始于非负状态空间,交通状态在演化过程中保持非负,如路段内车辆数、 车辆排队、 密度、 占有率等,具有这类性质的系统称为正系统[21]. 具有状态非负约束的问题广泛存在于实际系统中,传统控制理论各方向在正系统领域中均有相应研究,详见文[21]中介绍. 虽然,正系统理论成果在众多领域中已有应用,但其理论成果在交通控制领域中应用仍缺乏系统研究.
基于上述分析,本文采用一类正系统模型——Compartment系统对网络交通流演化建模,可描述具有任意控制结构的网络过饱和特征,系统状态非负性约束由系统自身性质保证. 给定网络车流输入,由非负矩阵理论,网络存在唯一稳定平衡点,给出平衡点解析计算公式,建立了网络稳态与输入之间的定量关系. 由此,提出网络稳态信号控制律,为路段绿时状态反馈控制律,信号控制为分布式. 若网络内各路段交通状态稳态值均相同,则系统实现交通状态一致; 若网络内路段集合划分为有限子集,每个子集内路段交通状态稳态值相同,则系统实现交通状态分群一致. 因此,文[18-20]中一致与分群一致信号控制思想为本文中信号控制方法的特殊情况. 选取实际网络拓扑,将本文信号控制方法与定时控制方法进行比较,说明本文方法的优势与适用场景.
2 交通网络Compartment系统模型交通状态(如: 交通密度、 占有率等)在随时间演化过程中均为非负. 因此,交通控制系统是典型正系统. 本节给出交通网络信号控制Compartment系统模型,该模型可描述具有任意拓扑的网络及网络过饱和特征.
采用J表示网络内交叉口编号集合; V={1,2,…}表示网络内路段编号集合; VS、 VD与VI分别表示边界输入与输出路段、 内部路段编号集合. 网络内路段具有车辆存储能力,可视为Compartment, 路段间车流的传输即为Compartment间状态量的传输.
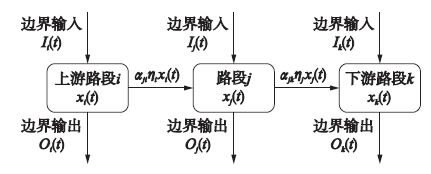
图 1给出交通网络Compartment系统结构. 假定网络内部路段数量为n. 图 1中xj(t),j∈VI为t∈N时刻路段j内车辆数,其中N为自然数集合; Ij(t)≥0与Oj(t)≥0分别表示路段j采样周期T>0内边界路段车流输入与输出. 从而,路段j内车辆数量演化满足如下方程:
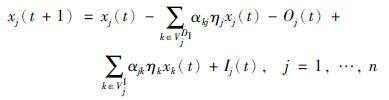
|
(1) |
式中,0<ηj≤1,j∈VI为采样周期内路段j的车辆泄流比例,定义为采样周期内路段j放行车辆总量与当前时刻路段内车辆数量之比; αkj≥0表示路段j到路段k的车流转向或分配比例; VjDI与VjI分别表示路段j的下游与上游内部路段集合; Ij(t)与Oj(t)分别为
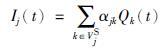
|
(2) |

|
(3) |
式中,VjS表示路段j上游边界输入路段集合; Qk(t)表示边界输入路段k采样周期内的车流输入; VjDS表示路段j下游边界输出路段集合.
|
| 图 1 交通网络Compartment系统模型 Figure 1 Compartment system model of traffic networks |
令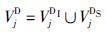
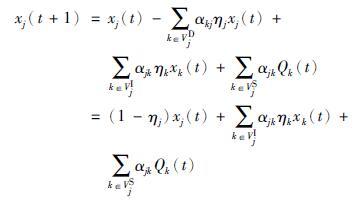
|
(4) |
式中,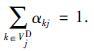
下面2条假定成立:
假定1 网络内信号控制交叉口处于同一信号控制子区,采用公共信号周期C,且方程(4)采样周期为T=C;
假定2 网络内路段VS∪VI上车辆以饱和流驶离停车线.
注1 为便于网络信号协调,处于同一信号控制子区内的路口采用公共信号周期. 方程(4)的采样周期为网络公共信号周期,意义在于: 简化网络交通流建模及优化,即只考虑路段内车流在周起点上的变化,忽略信号周期内路段上车流的波动,从而消除信号灯红—绿切换离散变量的影响,参见文[2-3]中详细论述; 网络信号周期C可根据交通历史数据离线或网络当前状态在线等外部优化程序确定,本文重点考虑给定周期下绿信比的设计方法.
注2 方程(4)中假定路段周期车辆泄流比例ηi≤1,i∈VI,其直观意义为信号周期内驶入下游路段的车辆总数不超过当前时刻路段内的车辆数. 若将路段内车辆数量理解为车辆排队,则路段内车辆排队在信号周期内无法完全消散,即方程(4)描述网络过饱和状态场景.
注3 方程(4)中边界输入Qi(t),i∈VS受信号灯控制,驶入下游路段车辆获得信号绿时可事先给定,需保证周期内Qi(t)辆车得以输入; 例如,假定i∈VS有3个下游路段jk,k=1,2,3. gijk(t),k=1,2,3为路段i驶入相应下游路段车流获得的有效绿时,则有
进一步,将方程(4)写为向量形式:

|
(5) |
式中,x(t)=[x1(t),…,xn(t)]T∈Rn为网络状态向量; A=[aij]∈Rn×n为状态矩阵,其对角线元素为: aii=1-ηi,i=1,…,n,非对角线元素为

|


|
系统(5)中状态矩阵A为非负矩阵,即矩阵元素均为非负,且列和满足: 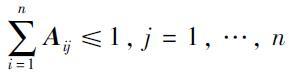
本节考虑系统(5)平衡点存在性与稳定性问题. 设E∈Rn×n为单位矩阵,矩阵


|
下面介绍本节所需矩阵论中相关结果. 符号“P>0”表示矩阵或向量P中元素均大于或等于0,且P≠0; “P

|
式中,Pi(i=1,2,3)为相应维数方阵; 矩阵P=[pij]∈Rn×n对应具有n个顶点有向图G(P): 若pij≠0,则存在顶点i到顶点j的有向边; 一个有向图为强连通,如果任意2个顶点间均存在有向路径; 矩阵P为不可约矩阵的充分必要条件是G(P)为强连通(参见文[22]定理2.7).
下面给出本节主要结果.
定理1 考虑网络信号控制模型(5),给定系统边界输入Q=[Q1,…,Qm]T
(1) 矩阵=E-A为非奇异M矩阵;
(2) 系统(5)存在唯一平衡点>0,且为全局渐近稳定;
(3) 平衡点
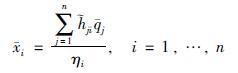
|
(6) |
式中,
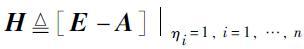
证明
1) 令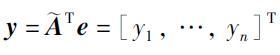


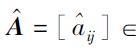

|
根据矩阵
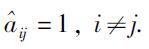
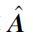
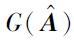
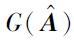
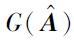
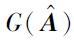



2) 令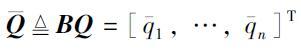
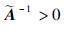
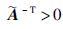
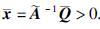


3) 设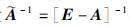

|
式中,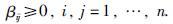
采用VjDI表示路段j∈VI下游内部路段集合,将矩阵[E-A]-1第i(i=1,…,n)行与矩阵[E-A]相乘可得如下n个线性方程组:
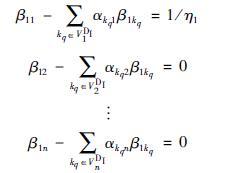
|
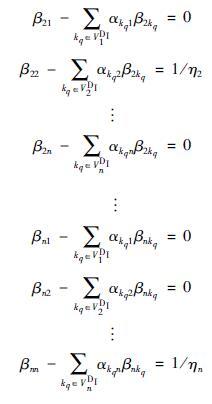
|
将上面各方程组写为向量形式可得:

|
(7) |
式中,矩阵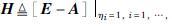
令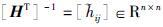
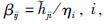
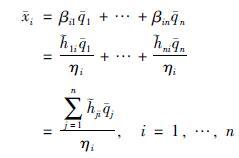
|
注4 由式(6)可知: 路段稳态值xi与网络内路段车流转向或分配比例、 边界路段车流输入及路段周期车辆泄流比例有关,且随着车流输入增加而增大. 若式(6)中车流放行比例ηi=1,即交通临界状态为系统稳态,则有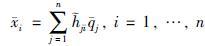
采用xj,max>0,j=1,…,n表示路段j的容量,称ρj=xj/xj,max为路段j内车辆相对占有率,可反应路段车辆拥挤程度.
假定内部路段集合VI划分为1≤p≤n个非空不交子集Ωi,i=1,…,p,即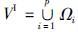
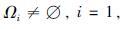
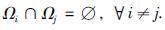
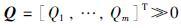
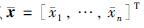
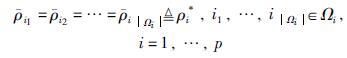
|
(8) |
式中,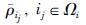
式(8)意味着: 系统(5)收敛到稳态时,可使路段内车辆相对占有率达到一致,从而实现网络内车流的均衡分布,降低网络局部拥堵. 式(8)包含2种特殊情况: p=1,即网络内部路段车辆相对占有率稳态值均相同; p=n, 即网络内部路段车辆相对占有率稳态值均不同. 根据实际需求对路段集合进行划分.
根据路段周期车辆泄流比例0<ηj≤1,j∈VI的定义,ηj与相应流向绿灯时间的关系如下:

|
式中,sjk>0,j∈VI为流向j→k的饱和流; gjk(t)=γjkgj(t),j∈VI为由路段j驶入路段k的车流获得的绿时,其中,gj(t)为路段j周期内获得的总绿时,γjk≥0为流向j→k的绿时分配比例系数,满足
进一步,考虑周期内路段各流向绿时的分配问题. 路段j到下游路段k流向绿时分配比例系数由下式确定:
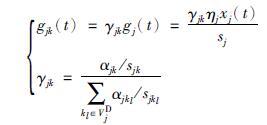
|
(9) |
式中,αjk/sjk可理解为j→k流向的流量比,即按各流向的负荷分配路段总绿时.
考虑实际应用,进一步求解满足周期、 绿时约束的各相位绿时. 考虑网络内信号交叉口j,假定包含q>1个信号相位,且每个信号相位包含li个非冲突受控车流,i=1,…,q. 令gjki(t),i=1,…,q; k=1,…,li表示相位i内由式(9)确定的各流向绿时,则满足相位绿时及周期约束的相位绿时Gji,i=1,…,q为

|
式中,Gjimin与Gjimax分别为交叉口j信号相位i最短与最长绿时,C为网络周期,Lj为周期相位总损失时间.
上述各路口局部凸优化问题易于在线求解. 本文提出的信号控制设计方法称为交通网络稳态信号控制(steady-state signal control, SSC),在给定网络公共周期下,SSC方法以网络均衡为目标实时调节网络交通流. 下一节将SSC方法应用于一个拓扑网络,并与定时信号控制方法(fixed-time signal control, FSC)进行比较.
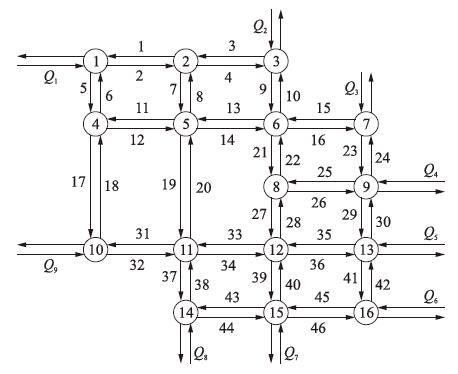
5 仿真与比较以北京市奥林匹克公园地区拓扑网络为例,在VISSIM软件中建立网络仿真环境,比较分析SSC方法与FSC方法的性能及SSC方法的适用场景. 路网拓扑结构如图 2所示,包含46个内部路段和9个输入与输出路段. 构建4种车流输入模式以模拟网络不同饱和程度,即低需求、 中低需求、 中高需求与高需求,每种需求下系统稳态值由式(6)计算. 根据路段的空间位置及交通历史数据对网络内部路段集合VI进行划分,选取各路段周期车辆泄流比例0<ηj≤1,j∈VI使得各路段子集稳态车辆相对占有率相同,即满足式(8).
|
| 图 2 仿真网络拓扑 Figure 2 Topology of simulation network |
网络内信号路口处于同一信号控制子区,以总通行量、 平均延误与平均停车次数为网络性能指标,SSC方法与FSC方法在4种需求下的仿真结果如表 1所示,其中性能指标由VISSIM仿真器计算. 分析表 1中实验结果: 当网络需求为低需求与中低需求2种模式时,网络处于非饱和状态,FSC方法优于SSC方法,其原因在于: 当网络处于非饱和状态,FSC方法能够在信号周期内清空路口各关键方向车辆排队,使得车辆延误尽可能小,而SSC方法假定路段车辆泄流比例不超过1,意味着车辆排队无法在周期内完全消散,从而增加了车辆延误; 当网络需求为中高需求与高需求2种模式时,网络处于过饱和状态,车辆排队无法在信号周期内完全消散,与SSC方法特性相吻合. 因此,与FSC方法相比,SSC方法能较大程度改善网络总体性能.
| 总通行量/veh | 平均延误/s | 平均停车次数 | ||||
| FSC | SSC | FSC | SSC | FSC | SSC | |
| 低需求 | 4 413 | -0.75% | 87 | +18.4% | 2.5 | +4% |
| 中低需求 | 6 522 | -2.3% | 120 | +31.67% | 3.0 | +30% |
| 中高需求 | 6 408 | +8.11% | 408 | -27.21% | 10.7 | -31.78 |
| 高需求 | 5 153 | +26.37% | 647 | -36.32% | 13.8 | -22.46% |
| 注:“-”减少; “+”增加. | ||||||
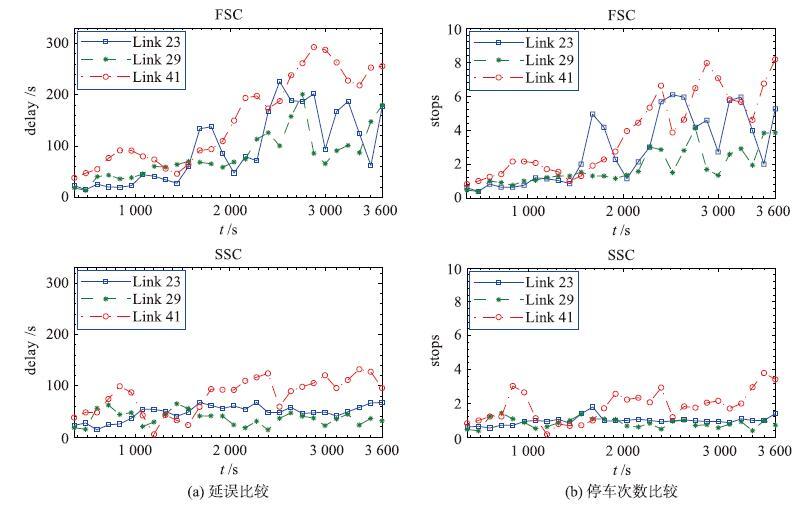
进一步,选择网络内3个路段分析FSC方法与SSC方法的性能及SSC方法的优势,路段标号为23、 29与41,3个路段位于一条路径上,参见图 2中网络拓扑. 图 3与图 4分别给出3个路段中高需求及高需求下路段延误与停车次数的时间演化. 由图 3与图 4中仿真结果可知: SSC方法能较大程度地改善路段性能,且保持路段内性能指标平稳变化. 进一步,分析图 3中仿真结果: 由于FSC方法不能响应车流动态变化,路段内延误及停车次数随时间增加,而SSC方法为路段状态反馈控制策略,能够响应动态变化车流,路段内延误与停车次数均有较大程度减少,缓解了局部交通拥堵; 分析图 4中仿真结果: 在网络高需求下,采用FSC方法网络内交通流分布不均衡加剧,路段内延误及停车次数出现较大波动. 如图 4所示,下游路段41内虽有空间,但未被充分利用,使得上游路段23与29产生局部拥堵,可能导致溢流现象. 而SSC方法能均衡网络内交通流分布,提升各路段内空间利用率.
|
| 图 3 中高需求下路段延误与停车次数比较 Figure 3 Comparison between delay and stops in chosen links under moderate traffic demand |

|
| 图 4 高需求下路段延误与停车次数比较 Figure 4 Comparison between delay and stops in chosen links under high traffic demand |
综上分析,根据SSC方法特性,网络较高需求下控制效果更佳,可均衡网络内车流分布和提升网络空间利用效率. 同时,SSC方法为分布式信号控制方法,具有鲁棒性,且易于执行与实际应用.
6 结论本文采用Compartment正系统对网络车流演化建模,建立了网络稳态与网络控制结构及边界输入间的定量解析关系,以网络车辆相对占有率均衡为控制目标,提出网络稳态信号控制方法. 通过实验分析并结合SSC方法性质,本文信号控制方法适于高需求网络条件.
本文将控制理论中一致性控制思想引入交通控制,特别是对于过饱和网络,交通状态达到一致或分群一致意味着网络内交通流实现某种均衡. 当前,过饱和网络控制为交通控制领域中难题,本文控制方法为过饱和网络控制提供了新的研究思路. 另外,本文信号控制方法总体路线与文[2-3]中TUC策略相近,说明其是可行的.
本文假定网络周期及相位差已给定,在此基础上给出相位绿灯时间的反馈控制规律,进一步研究工作包括两个方面: 考察更为广泛的拓扑网络,验证本文信号控制方法,并与其它方法进行比较; 结合正系统与交通流理论,研究网络周期与相位差的反馈控制规律.
| [1] | Papageorgiou M, Diakaki C, Dinopoulou V, et al. Review of road traffic control strategies[J]. Proceedings of the IEEE , 2003, 91 (12) : 2043–2067. DOI:10.1109/JPROC.2003.819610 |
| [2] | Diakaki C, Papageorgiou M, Aboudolas K. A multivariable regulator approach to traffic-responsive network-wide signal control[J]. Control Engineering Practice , 2002, 10 (2) : 183–195. DOI:10.1016/S0967-0661(01)00121-6 |
| [3] | Aboudolas K, Papageorgiou M, Kosmatopoulos E. Store-and-forward based methods for the signal control problem in large-scale congested urban road networks[J]. Transportation Research Part C: Emerging Technologies , 2009, 17 (2) : 163–174. DOI:10.1016/j.trc.2008.10.002 |
| [4] | Ioslovich I, Haddad J, Gutman P O, et al. Optimal traffic control synthesis for an isolated intersection[J]. Control Engineering Practice , 2011, 19 (8) : 900–911. DOI:10.1016/j.conengprac.2011.05.004 |
| [5] | Lin S, Schutter B D, Xi Y G, et al. Fast model predictive control for urban road networks via MILP[J]. IEEE Transactions on Intelligent Transportation Systems , 2011, 12 (3) : 846–856. DOI:10.1109/TITS.2011.2114652 |
| [6] | Schutter B D. Optimizing acyclic traffic signal switching sequences through an extended linear complementarity problem formulation[J]. European Journal of Operational Research , 2002, 139 (2) : 400–415. DOI:10.1016/S0377-2217(01)00364-2 |
| [7] | Haddad J, Schutter B D, Mahalel D, et al. Optimal steady-state control for isolated traffic intersections[J]. IEEE Transactions on Automatic Control , 2010, 55 (11) : 2612–2617. DOI:10.1109/TAC.2010.2060245 |
| [8] | Kouvelas A, Aboudolas K, Papageorgiou M, et al. A hybrid strategy for real-time traffic signal control of urban road networks[J]. IEEE Transactions on Intelligent Transportation Systems , 2011, 12 (3) : 884–894. DOI:10.1109/TITS.2011.2116156 |
| [9] | 陈阳舟, 李宏峰, 倪金. T形交叉口信号配时的周期线性微分自动机建模与分析[J]. 控制理论与应用 , 2011, 28 (12) : 1773–1778. Chen Y Z, Li H F, Ni J. Modeling and analysis of cyclic linear differential automata for T-intersection signal timing[J]. Control Theory & Applications , 2011, 28 (12) : 1773–1778. |
| [10] | He Z H, Chen Y Z, Shi J J, et al. Steady-state control for signalized intersections modeled as switched server system[C]//Proceedings of the 2013 American Control Conference. Piscataway NJ, USA: IEEE, 2013: 842-847. |
| [11] | 何忠贺, 陈阳舟, 石建军. 切换服务系统的稳定性及交叉口信号配时[J]. 控制理论与应用 , 2013, 30 (2) : 194–200. He Z H, Chen Y Z, Shi J J. Stability of switched server system and signal timing of intersection[J]. Control Theory & Applications , 2013, 30 (2) : 194–200. |
| [12] | 向伟铭, 肖建, 蒋阳升. 基于切换系统的过饱和信号交叉口混杂控制[J]. 交通运输系统工程与信息 , 2014, 14 (2) : 57–61. Xiang W M, Xiao J, Jiang Y S. Hybrid control for over-saturated signalized intersection based on switched system[J]. Journal of Transportation Systems Engineering and Information Technology , 2014, 14 (2) : 57–61. |
| [13] | 陈智, 刘小明, 刘文婷, 等. 过饱和交叉口交通信号模糊关联控制方法[J]. 信息与控制 , 2014, 43 (3) : 374–380. Chen Z, Liu X M, Liu W T, et al. Interconnected control of traffic signals at oversaturated intersections using fuzzy control method[J]. Information and Control , 2014, 43 (3) : 374–380. |
| [14] | Kosmatopoulos E, Papageorgiou M, Bielefeldt C, et al. International comparative field evaluation of a traffic-responsive signal control strategy in three cities[J]. Transportation Research Part A: Policy and Practice , 2006, 40 (5) : 399–413. DOI:10.1016/j.tra.2005.08.004 |
| [15] | Jr Kraus W, Souza F A D, Kosmatopoulos E B, et al. Cost effective real-time traffic signal control using the TUC strategy[J]. IEEE Intelligent Transportation Systems Magazine , 2010, 2 (4) : 6–17. DOI:10.1109/MITS.2010.939916 |
| [16] | 闵海波, 刘源, 王仕成, 等. 多个体协调控制综述[J]. 自动化学报 , 2012, 38 (10) : 1557–1570. DOI:10.3724/SP.J.1004.2012.01557 Min H B, Liu Y, Wang S C, et al. An overview on coordination control problem of multi-agent system[J]. Acta Automatica Sinica , 2012, 38 (10) : 1557–1570. DOI:10.3724/SP.J.1004.2012.01557 |
| [17] | Xia W G, Cao M. Cluster synchronization algorithms[C]//Proceedings of the 2010 American Control Conference. Piscataway NJ, USA: IEEE, 2010: 6513-6518. |
| [18] | He Z H, Chen Y Z, Shi J J, et al. Consensus based approach to the signal control of urban traffic networks[J]. Procedia-Social and Behavioral Sciences , 2013, 96 : 2511–2522. DOI:10.1016/j.sbspro.2013.08.281 |
| [19] | Wang L, Li D, Liu X M, et al. Regional traffic state consensus optimization based on computational experiments[C]//Proceedings of the 16th International IEEE Annual Conference onIntelligent Transportation Systems. Piscataway NJ, USA: IEEE, 2013: 1547-1552. |
| [20] | 王力, 李岱, 何忠贺, 等. 基于多智能体分群同步的城市路网交通控制[J]. 控制理论与应用 , 2014, 31 (11) : 1448–1456. Wang L, Li D, He Z H, et al. Urban traffic network control based on cluster consensus of multi-agent systems[J]. Control Theory & Applications , 2014, 31 (11) : 1448–1456. |
| [21] | Haddad W M, Chellaboina V, Hui Q. Nonnegative and compartmental dynamical systems[M]. Princeton, NJ, USA: Princeton University Press , 2010 . |
| [22] | Berman A, Plemmons R J. Nonnegative matrices in the mathematical sciences[M]. Philadelphia, PA, USA: SIAM , 1994 . |



